3.2E: Exercises
- Page ID
- 90231
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Exercise \(\PageIndex{1}\)
For exercises 1 - 3, use the direction field below from the differential equation \( y'=−2y.\) Sketch the graph of the solution for the given initial conditions.
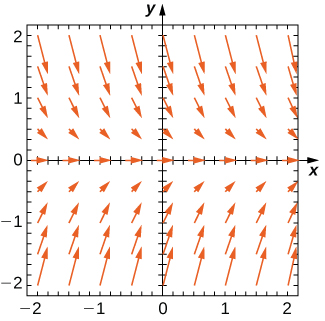
1) \( y(0)=1\)
2) \( y(0)=0\)
- Answer:
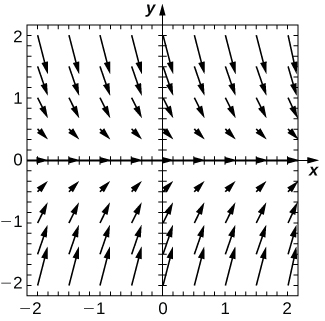
3) \( y(0)=−1\)
4) Are there any equilibria among the solutions of the differential equation from exercises 1 - 3? List any equilibria along with their stabilities.
- Answer:
- \( y=0\) is a stable equilibrium
Exercise \(\PageIndex{2}\)
For exercises 5 - 7, use the direction field below from the differential equation \( y'=y^2−2y\). Sketch the graph of the solution for the given initial conditions.
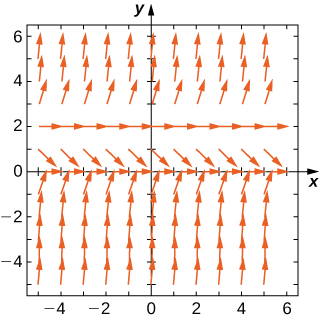
5) \( y(0)=3\)
6) \( y(0)=1\)
- Answer:
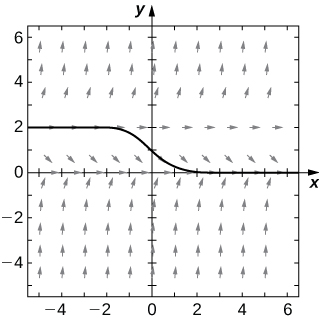
7) \( y(0)=−1\)
8) Are there any equilibria among the solutions of the differential equation from exercises 5 - 7? List any equilibria along with their stabilities.
- Answer:
- \( y=0\) is a stable equilibrium and \( y=2\) is unstable
- Answer
-
Add texts here. Do not delete this text first.
Exercise \(\PageIndex{3}\)
In exercises 9 - 13, draw the direction field for the following differential equations, then solve the differential equation. Draw your solution on top of the direction field. Does your solution follow along the arrows on your direction field?
9) \( y'=t^3\)
10) \( y'=e^t\)
- Answer:
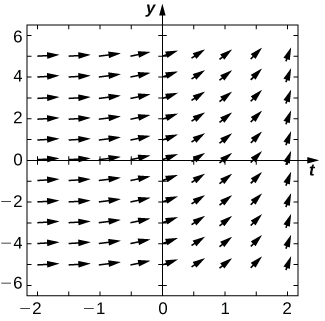
11) \( \dfrac{dy}{dx}=x^2\cos x\)
12) \( \dfrac{dy}{dt}=te^t\)
- Answer:
![A direction field over [-2, 2] in the x and y axes. The arrows point slightly down and to the right over [-2, 0] and gradually become vertical over [0, 2].](https://math.libretexts.org/@api/deki/files/2923/CNX_Calc_Figure_08_02_212.jpeg?revision=1&size=bestfit&width=342&height=344)
13) \( \dfrac{dx}{dt}=\cosh(t)\)
- Answer
-
Add texts here. Do not delete this text first.
Exercise \(\PageIndex{4}\)
In exercises 14 - 18, draw the directional field for the following differential equations. What can you say about the behavior of the solution? Are there equilibria? What stability do these equilibria have?
14) \( y'=y^2−1\)
- Answer:
- There appear to be equlibria at \(y = -1\) (stable) and \(y = 1\) (unstable).
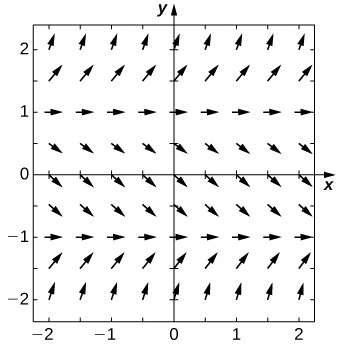
15) \( y'=y−x\)
16) \( y'=1−y^2−x^2\)
- Answer:
- There do not appear to be any equilibria.
![A direction field with arrows pointing down and to the right for nearly all points in [-2, 2] on the x and y axes. Close to the origin, the arrows become more horizontal, point to the upper right, become more horizontal, and then point down to the right again.](https://math.libretexts.org/@api/deki/files/2925/CNX_Calc_Figure_08_02_216.jpeg?revision=1&size=bestfit&width=342&height=344)
17) \( y'=t^2\sin y\)
18) \( y'=3y+xy\)
- Answer:
- There appears to be an unstable equilibrium at \(y=0.\)
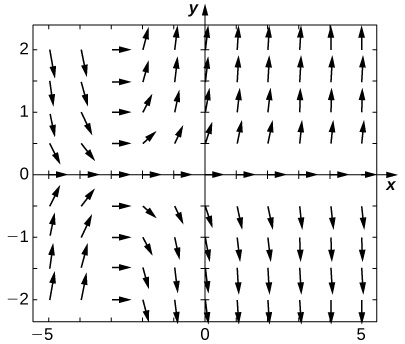
Exercise \(\PageIndex{5}\)
Match the direction field with the given differential equations. Explain your selections.
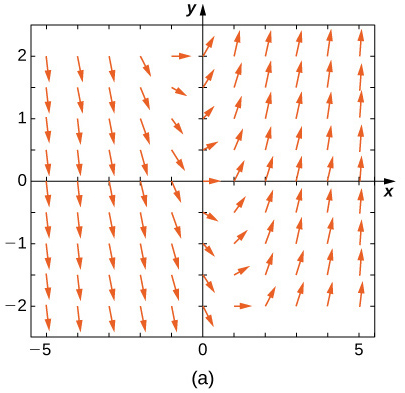
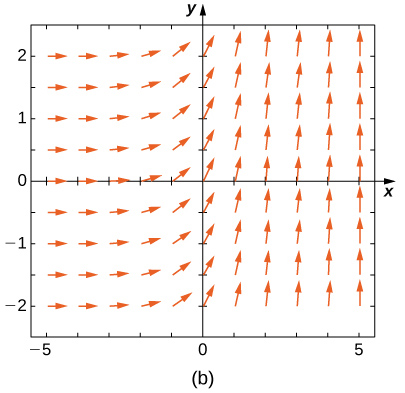
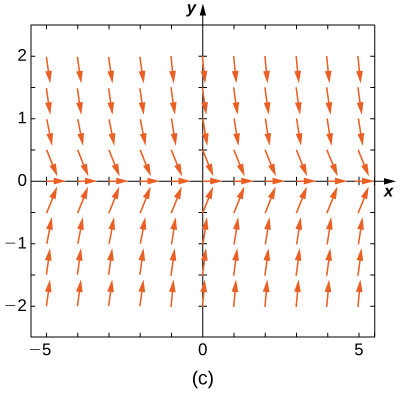
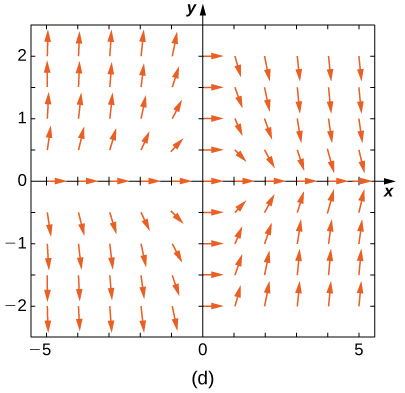
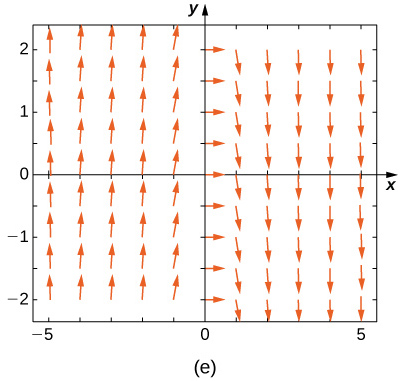
19) \( y'=−3y\)
20) \( y'=−3t\)
- Answer:
- \( E\)
21) \( y'=e^t\)
22) \( y'=\frac{1}{2}y+t\)
- Answer:
- \( A\)
23) \( y'=−ty\)
Exercise \(\PageIndex{6}\)
Match the direction field with the given differential equations. Explain your selections.
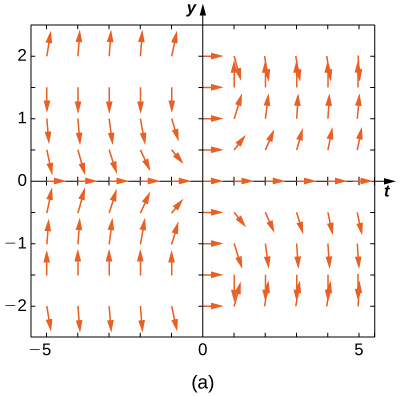
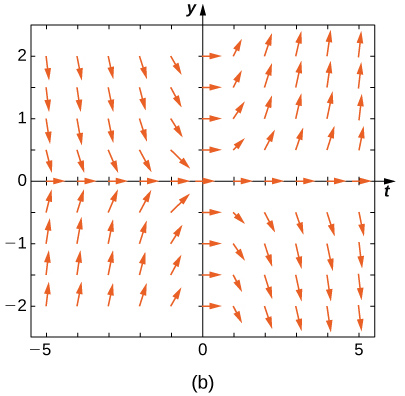
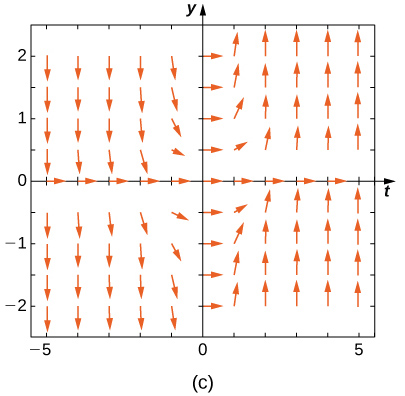
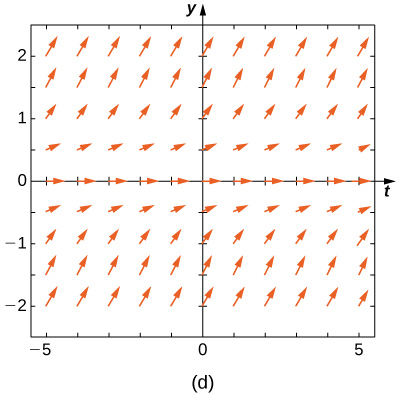
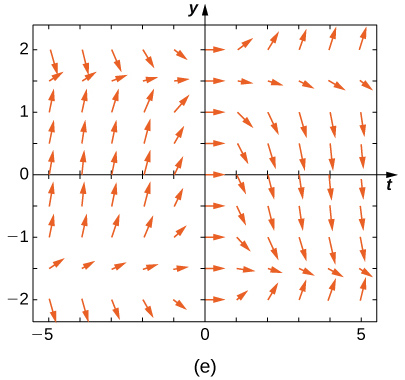
24) \( y'=t\sin y\)
- Answer:
- \( B\)
25) \( y'=−t\cos y\)
26) \( y'=t\tan y\)
- Answer:
- \( A\)
27) \( y'=\sin^2y\)
28) \( y'=y^2t^3\)
- Answer:
- \( C\)
Exercise \(\PageIndex{7}\)
Estimate the following solutions using Euler’s method with \( n=5\) steps over the interval \( t=[0,1].\) If you are able to solve the initial-value problem exactly, compare your solution with the exact solution. If you are unable to solve the initial-value problem, the exact solution will be provided for you to compare with Euler’s method. How accurate is Euler’s method?
29) \( y'=−3y,\quad y(0)=1\)
30) \( y'=t^2,\quad y(0)=1\)
- Answer:
- \( 2.24,\) exact: \( 3\)
Solution:
31) \( y′=3t−y,\quad y(0)=1.\) Exact solution is \( y=3t+4e^{−t}−3\)
32) \( y′=y+t^2,\quad y(0)=3.\) Exact solution is \( y=5e^t−2−t^2−2t\)
- Answer:
- \( 7.739364,\) exact: \( 5(e−1)\)
33) \( y′=2t,\quad y(0)=0\)
34) [T] \( y'=e^{x+y},y(0)=−1.\) Exact solution is \( y=−\ln(e+1−e^x)\)
- Answer:
- \( −0.2535,\) exact: \( 0\)
35) \( y′=y^2\ln(x+1),\quad y(0)=1.\) Exact solution is \( y=−\dfrac{1}{(x+1)(\ln(x+1)−1)}\)
36) \( y′=2^x,\quad y(0)=0.\) Exact solution is \( y=\dfrac{2^x−1}{\ln 2}\)
- Answer:
- \( 1.345,\) exact: \( \frac{1}{\ln(2)}\)
37) \( y′=y,\quad y(0)=−1.\) Exact solution is \( y=−e^x\).
38) \( y′=−5t,\quad y(0)=−2.\) Exact solution is \( y=−\frac{5}{2}t^2−2\)
- Answer:
- \( −4,\) exact: \( −1/2\)
Exercise \(\PageIndex{8}\)
Differential equations can be used to model disease epidemics. In the next set of problems, we examine the change of size of two sub-populations of people living in a city: individuals who are infected and individuals who are susceptible to infection. \( S\) represents the size of the susceptible population, and \( I\) represents the size of the infected population. We assume that if a susceptible person interacts with an infected person, there is a probability \( c\) that the susceptible person will become infected. Each infected person recovers from the infection at a rate \( r\) and becomes susceptible again. We consider the case of influenza, where we assume that no one dies from the disease, so we assume that the total population size of the two sub-populations is a constant number, \( N\). The differential equations that model these population sizes are
\( S'=rI−cSI\) and \( I'=cSI−rI.\)
Here \( c\) represents the contact rate and \( r\) is the recovery rate.
39) Show that, by our assumption that the total population size is constant \( (S+I=N),\) you can reduce the system to a single differential equation in \( I:I'=c(N−I)I−rI.\)
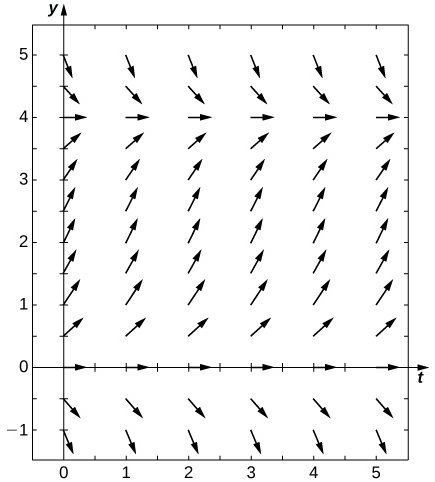
40) Assuming the parameters are \( c=0.5,N=5,\) and \( r=0.5\), draw the resulting directional field.
- Answer:
41) [T] Use computational software or a calculator to compute the solution to the initial-value problem \( y'=ty,y(0)=2\) using Euler’s Method with the given step size \( h\). Find the solution at \( t=1\). For a hint, here is “pseudo-code” for how to write a computer program to perform Euler’s Method for \( y'=f(t,y),y(0)=2:\)
Create function \( f(t,y)\)
Define parameters \( y(1)=y_0,t(0)=0,\) step size \( h\), and total number of steps, \( N\)
Write a for-loop:
for \( k=1\) to \( N\)
\( fn=f(t(k),y(k))\)
\( y(k+1)=y(k)+h*fn\)
\( t(k+1)=t(k)+h\)
42) Solve the initial-value problem for the exact solution.
- Answer:
- \( y'=2e^{t^2/2}\)
43) Draw the directional field
44) \( h=1\)
- Answer:
- \( 2\)
45) [T] \( h=10\)
46) [T] \( h=100\)
- Answer:
- \( 3.2756\)
47) [T] \( h=1000\)
48) [T] Evaluate the exact solution at \( t=1\). Make a table of errors for the relative error between the Euler’s method solution and the exact solution. How much does the error change? Can you explain?
- Answer:
- Exact solution: y =\( 2\sqrt{e}.\)
Step Size Error \( h=1\) \( 0.3935\) \( h=10\) \( 0.06163\) \( h=100\) \( 0.006612\) \( h=10000\) \( 0.0006661\)
- Answer
-
Add texts here. Do not delete this text first.
Exercise \(\PageIndex{9}\)
For exercises 49 - 53, consider the initial-value problem \( y'=−2y,\) with \(y(0)=2.\)
49) Show that \( y=2e^{−2x}\) solves this initial-value problem.
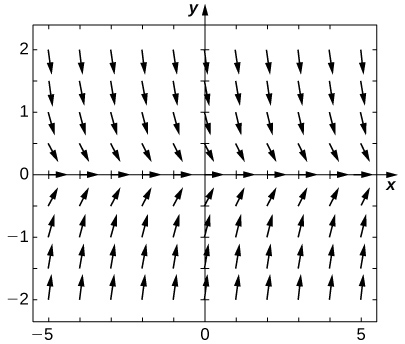
50) Draw the directional field of this differential equation.
- Answer:
51) [T] By hand or by calculator or computer, approximate the solution using Euler’s Method at \( t=10\) using \( h=5\).
52) [T] By calculator or computer, approximate the solution using Euler’s Method at \( t=10\) using \( h=100.\)
- Answer:
- \( 4.0741e^{−10}\)
53) [T] Plot exact answer and each Euler approximation (for \( h=5\) and \( h=100\)) at each h on the directional field. What do you notice?
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.

