5.1E: Exercises

Exercise $\PageIndex{1}$

In exercises 1 - 4, state whether each statement is true, or give an example to show that it is false.

1) If $\displaystyle \sum_{n=1}^∞a_nx^n$ converges, then $a_nx^n→0$ as $n→∞.$

Answer:

True. If a series converges then its terms tend to zero.

2) $\displaystyle \sum_{n=1}^∞a_nx^n$ converges at $x=0$ for any real numbers $a_n$.

3) Given any sequence $a_n$, there is always some $R>0$, possibly very small, such that $\displaystyle \sum_{n=1}^∞a_nx^n$ converges on $(−R,R)$.

Answer:

False. It would imply that $a_nx^n→0$ for $|x|<R$. If $a_n=n^n$, then $a_nx^n=(nx)^n$ does not tend to zero for any $x≠0$.

4) If $\displaystyle \sum_{n=1}^∞a_nx^n$ has radius of convergence $R>0$ and if $|b_n|≤|a_n|$ for all $n$, then the radius of convergence of $\displaystyle \sum_{n=1}^∞b_nx^n$ is greater than or equal to $R$.

 

Exercise $\PageIndex{2}$

5) Suppose that $\displaystyle \sum_{n=0}^∞a_n(x−3)^n$ converges at $x=6$. At which of the following points must the series also converge? Use the fact that if $\displaystyle \sum a_n(x−c)^n$ converges at $x$, then it converges at any point closer to $c$ than $x$.

a. $x=1$

b. $x=2$

c. $x=3$

d. $x=0$

e. $x=5.99$

f. $x=0.000001$

Answer:

It must converge on $(0,6]$ and hence at: a. $x=1$; b. $x=2$; c. $x=3$; d. $x=0$; e. $x=5.99$; and f. $x=0.000001$.

6) Suppose that $\displaystyle \sum_{n=0}^∞a_n(x+1)^n$ converges at $x=−2$. At which of the following points must the series also converge? Use the fact that if $\displaystyle \sum a_n(x−c)^n$ converges at $x$, then it converges at any point closer to $c$ than $x$.

a. $x=2$

b. $x=−1$

c. $x=−3$

d. $x=0$

e. $x=0.99$

f. $x=0.000001$

Answer

Add texts here. Do not delete this text first.

Exercise $\PageIndex{3}$

In the following exercises, suppose that $\left|\dfrac{a_{n+1}}{a_n}\right|→1$ as $n→∞.$ Find the radius of convergence for each series.

7) $\displaystyle \sum_{n=0}^∞a_n2^nx^n$

Answer:

$\left|\dfrac{a_{n+1}2^{n+1}x^{n+1}}{a_n2^nx^n}\right| =2|x|\left|\dfrac{a_{n+1}}{a_n}\right|→2|x|$ so $R=\frac{1}{2}$

8) $\displaystyle \sum_{n=0}^∞\frac{a_nx^n}{2^n}$

9) $\displaystyle \sum_{n=0}^∞\frac{a_nπ^nx^n}{e^n}$

Answer:

$\left|\dfrac{a_{n+1}(\dfrac{π}{e})^{n+1}x^{n+1}}{a_n(\dfrac{π}{e})^nx^n}\right| =\dfrac{π|x|}{e}\left|\dfrac{a_{n+1}}{a_n}\right|→\dfrac{π|x|}{e}$ so $R=\frac{e}{π}$

10) $\displaystyle \sum_{n=0}^∞\frac{a_n(−1)^nx^n}{10^n}$

11) $\displaystyle \sum_{n=0}^∞a_n(−1)^nx^{2n}$

Answer:

$\left|\dfrac{a_{n+1}(−1)^{n+1}x^{2n+2}}{a_n(−1)^nx^{2n}}\right| =|x^2|\left|\dfrac{a_{n+1}}{a_n}\right|→|x^2|$ so $R=1$

12) $\displaystyle \sum_{n=0}^∞a_n(−4)^nx^{2n}$

Answer

Add texts here. Do not delete this text first.

Exercise $\PageIndex{4}$

In exercises 13 - 22, find the radius of convergence $R$ and interval of convergence for $\displaystyle \sum a_nx^n$ with the given coefficients $a_n$.

13) $\displaystyle \sum_{n=1}^∞\frac{(2x)^n}{n}$

Answer:

$a_n=\dfrac{2^n}{n}$ so $\dfrac{a_{n+1}x}{a_n}→2x$. so $R=\frac{1}{2}$. When $x=\frac{1}{2}$ the series is harmonic and diverges. When $x=−\frac{1}{2}$ the series is alternating harmonic and converges. The interval of convergence is $I=\big[−\frac{1}{2},\frac{1}{2}\big)$.

14) $\displaystyle \sum_{n=1}^∞(−1)^n\frac{x^n}{\sqrt{n}}$

15) $\displaystyle \sum_{n=1}^∞\frac{nx^n}{2^n}$

Answer:

$a_n=\dfrac{n}{2^n}$ so $\dfrac{a_{n+1}x}{a_n}→\dfrac{x}{2}$ so $R=2$. When $x=±2$ the series diverges by the divergence test. The interval of convergence is $I=(−2,2)$.

16) $\displaystyle \sum_{n=1}^∞\frac{nx^n}{e^n}$

17) $\displaystyle \sum_{n=1}^∞\frac{n^2x^n}{2^n}$

Answer:

$a_n=\dfrac{n^2}{2^n}$ so $R=2$. When $x=±2$ the series diverges by the divergence test. The interval of convergence is $I=(−2,2).$

18) $\displaystyle \sum_{k=1}^∞\frac{k^ex^k}{e^k}$

19) $\displaystyle \sum_{k=1}^∞\frac{π^kx^k}{k^π}$

Answer:

$a_k=\dfrac{π^k}{k^π}$ so $R=\frac{1}{π}$. When $x=±\frac{1}{π}$ the series is an absolutely convergent $p$-series. The interval of convergence is $I=\left[−\frac{1}{π},\frac{1}{π}\right].$

20) $\displaystyle \sum_{n=1}^∞\frac{x^n}{n!}$

21) $\displaystyle \sum_{n=1}^∞\frac{10^nx^n}{n!}$

Answer:

$a_n=\dfrac{10^n}{n!},\dfrac{a_{n+1}x}{a_n}=\dfrac{10x}{n+1}→0<1$ so the series converges for all $x$ by the ratio test and $I=(−∞,∞)$.

22) $\displaystyle \sum_{n=1}^∞(−1)^n\frac{x^n}{\ln(2n)}$

Answer

Add texts here. Do not delete this text first.

Exercise $\PageIndex{5}$

In exercises 23 - 28, find the radius of convergence of each series.

23) $\displaystyle \sum_{k=1}^∞\frac{(k!)^2x^k}{(2k)!}$

Answer:

$a_k=\dfrac{(k!)^2}{(2k)!}$ so $\dfrac{a_{k+1}}{a_k}=\dfrac{(k+1)^2}{(2k+2)(2k+1)}→\dfrac{1}{4}$ so $R=4$

24) $\displaystyle \sum_{n=1}^∞\frac{(2n)!x^n}{n^{2n}}$

25) $\displaystyle \sum_{k=1}^∞\frac{k!}{1⋅3⋅5⋯(2k−1)}x^k$

Answer:

$a_k=\dfrac{k!}{1⋅3⋅5⋯(2k−1)}$ so $\dfrac{a_{k+1}}{a_k}=\dfrac{k+1}{2k+1}→\dfrac{1}{2}$ so $R=2$

26) $\displaystyle \sum_{k=1}^∞\frac{2⋅4⋅6⋯2k}{(2k)!}x^k$

27) $\displaystyle \sum_{n=1}^∞\frac{x^n}{(^{2n}_n)}$ where $(^n_k)=\dfrac{n!}{k!(n−k)!}$

Answer:

$a_n=\dfrac{1}{(^{2n}_n)}$ so $\dfrac{a_{n+1}}{a_n}=\dfrac{\big((n+1)!\big)^2}{(2n+2)!}\dfrac{2n!}{(n!)^2}=\dfrac{(n+1)^2}{(2n+2)(2n+1)}→\dfrac{1}{4}$ so $R=4$

28) $\displaystyle \sum_{n=1}^∞\sin^2nx^n$

Answer

Add texts here. Do not delete this text first.

Exercise $\PageIndex{6}$

In exercises 29 - 32, use the ratio test to determine the radius of convergence of each series.

29) $\displaystyle \sum_{n=1}^∞\frac{(n!)^3}{(3n)!}x^n$

Answer:

$\dfrac{a_{n+1}}{a_n}=\dfrac{(n+1)^3}{(3n+3)(3n+2)(3n+1)}→\dfrac{1}{27}$ so $R=27$

30) $\displaystyle \sum_{n=1}^∞\frac{2^{3n}(n!)^3}{(3n)!}x^n$

31) $\displaystyle \sum_{n=1}^∞\frac{n!}{n^n}x^n$

Answer:

$a_n=\dfrac{n!}{n^n}$ so $\dfrac{a_{n+1}}{a_n}=\dfrac{(n+1)!}{n!}\dfrac{n^n}{(n+1)^{n+1}}=(\dfrac{n}{n+1})^n→\dfrac{1}{e}$ so $R=e$

32) $\displaystyle \sum_{n=1}^∞\frac{(2n)!}{n^{2n}}x^n$

Answer

Add texts here. Do not delete this text first.

Exercise $\PageIndex{7}$

In the following exercises, given that $\displaystyle \frac{1}{1−x}=\sum_{n=0}^∞x^n$ with convergence in $(−1,1)$, find the power series for each function with the given center $a,$ and identify its interval of convergence.

33) $f(x)=\dfrac{1}{x};a=1$ (Hint: $\dfrac{1}{x}=\dfrac{1}{1−(1−x)})$

Answer:

$\displaystyle f(x)=\sum_{n=0}^∞(1−x)^n$ on $I=(0,2)$

34) $f(x)=\dfrac{1}{1−x^2};a=0$

35) $f(x)=\dfrac{x}{1−x^2};a=0$

Answer:

$\displaystyle \sum_{n=0}^∞x^{2n+1}$ on $I=(−1,1)$

36) $f(x)=\dfrac{1}{1+x^2};a=0$

37) $f(x)=\dfrac{x^2}{1+x^2};a=0$

Answer:

$\displaystyle \sum_{n=0}^∞(−1)^nx^{2n+2}$ on $I=(−1,1)$

38) $f(x)=\dfrac{1}{2−x};a=1$

39) $f(x)=\dfrac{1}{1−2x};a=0.$

Answer:

$\displaystyle \sum_{n=0}^∞2^nx^n$ on $\left(−\frac{1}{2},\frac{1}{2}\right)$

40) $f(x)=\dfrac{1}{1−4x^2};a=0$

41) $f(x)=\dfrac{x^2}{1−4x^2};a=0$

Answer:

$\displaystyle \sum_{n=0}^∞4^nx^{2n+2}$ on $\left(−\frac{1}{2},\frac{1}{2}\right)$

42) $f(x)=\dfrac{x^2}{5−4x+x^2};a=2$

Answer

Add texts here. Do not delete this text first.

Exercise $\PageIndex{8}$

Use the result of exercise 43 to find the radius of convergence of the given series in the subsequent exercises (44 - 47).

43) Explain why, if $|a_n|^{1/n}→r>0,$ then $|a_nx^n|^{1/n}→|x|r<1$ whenever $|x|<\frac{1}{r}$ and, therefore, the radius of convergence of $\displaystyle \sum_{n=1}^∞a_nx^n$ is $R=\frac{1}{r}$.

Answer:

$|a_nx^n|^{1/n}=|a_n|^{1/n}|x|→|x|r$ as $n→∞$ and $|x|r<1$ when $|x|<\frac{1}{r}$. Therefore, $\displaystyle \sum_{n=1}^∞a_nx^n$ converges when $|x|<\frac{1}{r}$ by the $n^{\text{th}}$ root test.

44) $\displaystyle \sum_{n=1}^∞\frac{x^n}{n^n}$

45) $\displaystyle \sum_{k=1}^∞\left(\frac{k−1}{2k+3}\right)^kx^k$

Answer:

$a_k=\left(\dfrac{k−1}{2k+3}\right)^k$ so $(a_k)^{1/k}→\frac{1}{2}<1$ so $R=2$

46) $\displaystyle \sum_{k=1}^∞(\frac{2k^2−1}{k^2+3})^kx^k$

47) $\displaystyle \sum_{n=1}^∞a_n=(n^{1/n}−1)^nx^n$

Answer:

$a_n=(n^{1/n}−1)^n$ so $(a_n)^{1/n}→0$ so $R=∞$

Answer

Add texts here. Do not delete this text first.

Exercise $\PageIndex{9}$

48) Suppose that $\displaystyle p(x)=\sum_{n=0}^∞a_nx^n$ such that $a_n=0$ if $n$ is even. Explain why $p(x)=p(−x).$

49) Suppose that $\displaystyle p(x)=\sum_{n=0}^∞a_nx^n$ such that $a_n=0$ if $n$ is odd. Explain why $p(x)=−p(−x).$

Answer:

We can rewrite $\displaystyle p(x)=\sum_{n=0}^∞a_{2n+1}x^{2n+1}$ and $p(x)=p(−x)$ since $x^{2n+1}=−(−x)^{2n+1}$.

50) Suppose that $\displaystyle p(x)=\sum_{n=0}^∞a_nx^n$ converges on $(−1,1]$. Find the interval of convergence of $p(Ax)$.

51) Suppose that $\displaystyle p(x)=\sum_{n=0}^∞a_nx^n$ converges on $(−1,1]$. Find the interval of convergence of $p(2x−1)$.

Answer:

If $x∈[0,1],$ then $y=2x−1∈[−1,1]$ so $\displaystyle p(2x−1)=p(y)=\sum_{n=0}^∞a_ny^n$ converges.

Answer

Add texts here. Do not delete this text first.

Exercise $\PageIndex{10}$

In the following exercises, suppose that $\displaystyle p(x)=\sum_{n=0}^∞a_nx^n$ satisfies $\displaystyle \lim_{n→∞}\frac{a_{n+1}}{a_n}=1$ where $a_n≥0$ for each $n$. State whether each series converges on the full interval $(−1,1)$, or if there is not enough information to draw a conclusion. Use the comparison test when appropriate.

52) $\displaystyle \sum_{n=0}^∞a_nx^{2n}$

53) $\displaystyle \sum_{n=0}^∞a_{2n}x^{2n}$

Answer:

Converges on $(−1,1)$ by the ratio test

54) $\displaystyle \sum_{n=0}^∞a_{2n}x^n$ (Hint:$x=±\sqrt{x^2}$)

55) $\displaystyle \sum_{n=0}^∞a_{n^2}x^{n^2}$ (Hint: Let $b_k=a_k$ if $k=n^2$ for some $n$, otherwise $b_k=0$.)

Answer:

Consider the series $\displaystyle \sum b_kx^k$ where $b_k=a_k$ if $k=n^2$ and $b_k=0$ otherwise. Then $b_k≤a_k$ and so the series converges on $(−1,1)$ by the comparison test.

Answer

Add texts here. Do not delete this text first.

Exercise $\PageIndex{11}$

56) Suppose that $p(x)$ is a polynomial of degree $N$. Find the radius and interval of convergence of $\displaystyle \sum_{n=1}^∞p(n)x^n$.

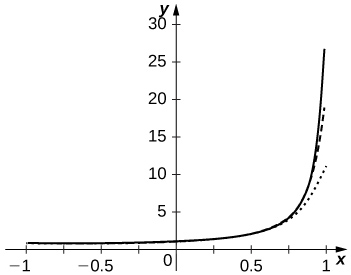
57) [T] Plot the graphs of $\dfrac{1}{1−x}$ and of the partial sums $\displaystyle S_N=\sum_{n=0}^Nx^n$ for $n=10,20,30$ on the interval $[−0.99,0.99]$. Comment on the approximation of $\dfrac{1}{1−x}$ by $S_N$ near $x=−1$ and near $x=1$ as $N$ increases.

Answer:

The approximation is more accurate near $x=−1$. The partial sums follow $\dfrac{1}{1−x}$ more closely as $N$ increases but are never accurate near $x=1$ since the series diverges there.

58) [T] Plot the graphs of $−\ln(1−x)$ and of the partial sums $\displaystyle S_N=\sum_{n=1}^N\frac{x^n}{n}$ for $n=10,50,100$ on the interval $[−0.99,0.99]$. Comment on the behavior of the sums near $x=−1$ and near $x=1$ as $N$ increases.

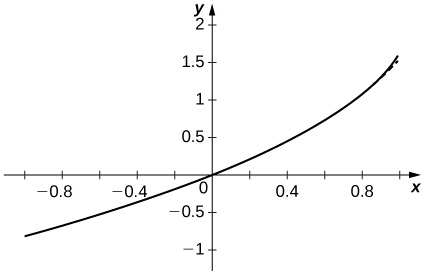
59) [T] Plot the graphs of the partial sums $\displaystyle S_n=\sum_{n=1}^N\frac{x^n}{n^2}$ for $n=10,50,100$ on the interval $[−0.99,0.99]$. Comment on the behavior of the sums near $x=−1$ and near $x=1$ as $N$ increases.

Answer:

The approximation appears to stabilize quickly near both $x=±1$.

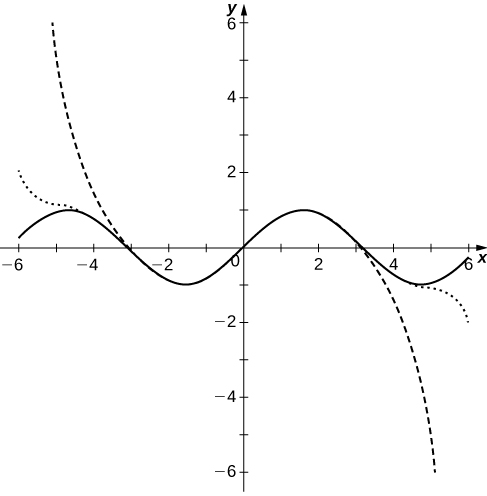
60) [T] Plot the graphs of the partial sums $\displaystyle S_N=\sum_{n=1}^N(\sin n) x^n$ for $n=10,50,100$ on the interval $[−0.99,0.99]$. Comment on the behavior of the sums near $x=−1$ and near $x=1$ as $N$ increases.

61) [T] Plot the graphs of the partial sums $\displaystyle S_N=\sum_{n=0}^N(−1)^n\frac{x^{2n+1}}{(2n+1)!}$ for $n=3,5,10$ on the interval $[−2π,2π]$. Comment on how these plots approximate $\sin x$ as $N$ increases.

Answer:

The polynomial curves have roots close to those of $\sin x$ up to their degree and then the polynomials diverge from $\sin x$.

62) [T] Plot the graphs of the partial sums $\displaystyle S_N=\sum_{n=0}^N(−1)^n\frac{x^{2n}}{(2n)!}$ for $n=3,5,10$ on the interval $[−2π,2π]$. Comment on how these plots approximate $\cos x$ as $N$ increases.

 

Answer

Add texts here. Do not delete this text first.

 

Contributors

Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.