6.2E: Excercises

Exercise $\PageIndex{1}$

For the following exercises, find the limit of the function.

1) $\displaystyle \lim_{(x,y)→(1,2)}x$

2) $\displaystyle \lim_{(x,y)→(1,2)}\frac{5x^2y}{x^2+y^2}$

Answer

Solution:$\displaystyle 2.0$

Exercise $\PageIndex{2}$

1) Show that the limit $\displaystyle \lim_{(x,y)→(0,0)}\frac{5x^2y}{x^2+y^2}$ exists and is the same along the paths: $\displaystyle y-axis$ and $\displaystyle x-axis$, and along $\displaystyle y=x$.

Exercise $\PageIndex{3}$

For the following exercises, evaluate the limits at the indicated values of $\displaystyle x$ and $\displaystyle y$. If the limit does not exist, state this and explain why the limit does not exist.

1) $\displaystyle \lim_{(x,y)→(0,0)}\frac{4x^2+10y^2+4}{4x^2−10y^2+6}$

Answer

Solution:$\displaystyle \frac{2}{3}$

2) $\displaystyle \lim_{(x,y)→(11,13)}\sqrt{\frac{1}{xy}}$

3) $\displaystyle \lim_{(x,y)→(0,1)}\frac{y^2sinx}{x}$

Answer

Solution:$\displaystyle 1$

4) $\displaystyle \lim_{(x,y)→(0,0)}sin(\frac{x^8+y^7}{x−y+10})$

5) $\displaystyle \lim_{(x,y)→(π/4,1)}\frac{ytanx}{y+1}$

Answer

Solution:$\displaystyle \frac{1}{2}$

6) $\displaystyle \lim_{(x,y)→(0,π/4)}\frac{secx+2}{3x−tany}$

7) $\displaystyle \lim_{(x,y)→(2,5)}(\frac{1}{x}−\frac{5}{y})$

Answer

Solution:$\displaystyle −\frac{1}{2}$

8) $\displaystyle \lim_{(x,y)→(4,4)}xlny$

9) $\displaystyle \lim_{(x,y)→(4,4)}e^{−x^2−y^2}$

Answer

Solution:$\displaystyle e^{−32}$

10) $\displaystyle \lim_{(x,y)→(0,0)}\sqrt{9−x^2−y^2}$

11) $\displaystyle \lim_{(x,y)→(1,2)}(x^2y^3−x^3y^2+3x+2y)$

Answer

Solution:$\displaystyle 11.0$

12) $\displaystyle \lim_{(x,y)→(π,π)}xsin(\frac{x+y}{4})$

13) $\displaystyle \lim_{(x,y)→(0,0)}\frac{xy+1}{x^2+y^2+1}$

Answer

Solution:$\displaystyle 1.0$

14) $\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2+y^2}{\sqrt{x^2+y^2+1}−1}$

15) $\displaystyle \lim_{(x,y)→(0,0)}ln(x^2+y^2)$

Answer

Solution:The limit does not exist because when $\displaystyle x$ and $\displaystyle y$ both approach zero, the function approaches $\displaystyle ln0$, which is undefined (approaches negative infinity).

Exercise $\PageIndex{4}$

For the following exercises, complete the statement.

1) A point $\displaystyle (x_0,y_0)$ in a plane region $\displaystyle R$ is an interior point of $\displaystyle R$ if _________________.

2) A point $\displaystyle (x_0,y_0)$ in a plane region R is called a boundary point of $\displaystyle R$ if ___________.

Answer

Solution:every open disk centered at $\displaystyle (x_0,y_0)$ contains points inside $\displaystyle R$ and outside $\displaystyle R$

Exercise $\PageIndex{5}$

For the following exercises, use algebraic techniques to evaluate the limit.

1) $\displaystyle \lim_{(x,y)→(2,1)}\frac{x−y−1}{\sqrt{x−y}−1}$

2) $\displaystyle \lim_{(x,y)→(0,0)}\frac{x^4−4y^4}{x^2+2y^2}$

Answer

Solution:$\displaystyle 0.0$

3) $\displaystyle \lim_{(x,y)→(0,0)}\frac{x^3−y^3}{x−y}$

4) $\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2−xy}{\sqrt{x}−\sqrt{y}}$

Answer

Solution:$\displaystyle 0.00$

Exercise $\PageIndex{6}$

For the following exercises, evaluate the limits of the functions of three variables.

1) $\displaystyle lim_{(x,y,z)→(1,2,3)}\frac{xz^2−y^2z}{xyz−1}$

2) $\displaystyle \lim_{(x,y,z)→(0,0,0)}\frac{x^2−y^2−z^2}{x^2+y^2−z^2}$

Answer

Solution:The limit does not exist.

Exercise $\PageIndex{7}$

For the following exercises, evaluate the limit of the function by determining the value the function approaches along the indicated paths. If the limit does not exist, explain why not.

1) $\displaystyle \lim_{(x,y)→(0,0)}\frac{xy+y^3}{x^2+y^2}$

a. Along the $\displaystyle x-axis$ $\displaystyle (y=0)$

b. Along the $\displaystyle y-axis$ $\displaystyle (x=0)$

c. Along the path $\displaystyle y=2x$

2) Evaluate $\displaystyle \lim_{(x,y)→(0,0)}\frac{xy+y^3}{x^2+y^2}$ using the results of previous problem.

Answer

Solution: The limit does not exist. The function approaches two different values along different paths.

3) $\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2y}{x^4+y^2}$

a. Along the $\displaystyle x-axis$ $\displaystyle (y=0)$

b. Along the $\displaystyle y-axis$ $\displaystyle (x=0)$

c. Along the path $\displaystyle y=x^2$

4) Evaluate $\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2y}{x^4+y^2}$ using the results of previous problem.

Answer

Solution: The limit does not exist because the function approaches two different values along the paths.

Exercise $\PageIndex{8}$

Discuss the continuity of the following functions. Find the largest region in the $\displaystyle xy-plane$ in which the following functions are continuous.

1) $\displaystyle f(x,y)=sin(xy)$

2) $\displaystyle f(x,y)=ln(x+y)$

Answer

Solution:The function $\displaystyle f$ is continuous in the region $\displaystyle y>−x.$

3) $\displaystyle f(x,y)=e^{3xy}$

4) $\displaystyle f(x,y)=\frac{1}{xy}$

Answer

Solution:The function $\displaystyle f$ is continuous at all points in the $\displaystyle xy-plane$ except at $\displaystyle (0,0).$

Exercise $\PageIndex{9}$

Discuss the continuity of the following functions. Find the largest region in the $\displaystyle xy-plane$ in which the following functions are continuous.

31) $\displaystyle f(x,y)=sin(xy)$

32) $\displaystyle f(x,y)=ln(x+y)$

Answer

Solution:The function $\displaystyle f$ is continuous in the region $\displaystyle y>−x.$

33) $\displaystyle f(x,y)=e^{3xy}$

34) $\displaystyle f(x,y)=\frac{1}{xy}$

Answer

Solution:The function $\displaystyle f$ is continuous at all points in the $\displaystyle xy-plane$ except at \(\displaystyle (0,0).\

Exercise $\PageIndex{10}$

For the following exercises, determine the region in which the function is continuous. Explain your answer.

2) $\displaystyle f(x,y)=\frac{x^2y}{x^2+y^2}$

2) $\displaystyle f(x,y)=$$\displaystyle \begin{cases}\frac{x^2y}{x^2+y^2} & if(x,y)≠(0,0)\\0 & if(x,y)=(0,0)\end{cases}$

(Hint: Show that the function approaches different values along two different paths.)

Answer

Solution:The function is continuous at $\displaystyle (0,0)$ since the limit of the function at $\displaystyle (0,0)$ is $\displaystyle 0$, the same value of $\displaystyle f(0,0).$

3) $\displaystyle f(x,y)=\frac{sin(x^2+y^2)}{x^2+y^2}$

Exercise $\PageIndex{11}$

1) Determine whether $\displaystyle g(x,y)=\frac{x^2−y^2}{x^2+y^2}$ is continuous at $\displaystyle (0,0)$.

Answer

Solution:The function is discontinuous at $\displaystyle (0,0).$ The limit at $\displaystyle (0,0)$ fails to exist and $\displaystyle g(0,0)$ does not exist.

Exercise $\PageIndex{11}$

39) Create a plot using graphing software to determine where the limit does not exist. Determine the region of the coordinate plane in which $\displaystyle f(x,y)=\frac{1}{x^2−y}$ is continuous.

40) Determine the region of the $\displaystyle xy-plane$ in which the composite function $\displaystyle g(x,y)=arctan(\frac{xy^2}{x+y})$ is continuous. Use technology to support your conclusion.

Answer

Solution:Since the function $\displaystyle arctanx$ is continuous over $\displaystyle (−∞,∞), g(x,y)=arctan(\frac{xy^2}{x+y})$ is continuous where $\displaystyle z=\frac{xy^2}{x+y}$ is continuous. The inner function $\displaystyle z$ is continuous on all points of the $\displaystyle xy-plane$ except where $\displaystyle y=−x.$ Thus, $\displaystyle g(x,y)=arctan(\frac{xy^2}{x+y})$ is continuous on all points of the coordinate plane except at points at which $\displaystyle y=−x.$

41) Determine the region of the $\displaystyle xy-plane$ in which $\displaystyle f(x,y)=ln(x^2+y^2−1)$ is continuous. Use technology to support your conclusion. (Hint: Choose the range of values for $\displaystyle x$ and $\displaystyle y$ carefully!)

42) At what points in space is $\displaystyle g(x,y,z)=x^2+y^2−2z^2$ continuous?

Answer

Solution:All points $\displaystyle P(x,y,z)$ in space.

43) At what points in space is $\displaystyle g(x,y,z)=\frac{1}{x^2+z^2−1}$ continuous?

44) Show that $\displaystyle \lim_{(x,y)→(0,0)}\frac{1}{x^2+y^2}$ does not exist at $\displaystyle (0,0)$ by plotting the graph of the function.

Answer

Solution:The graph increases without bound as $\displaystyle x$ and $\displaystyle y$ both approach zero.

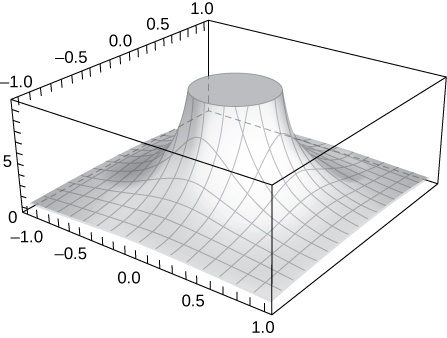
45) [T] Evaluate $\displaystyle \lim_{(x,y)→(0,0)}\frac{−xy^2}{x^2+y^4}$ by plotting the function using a CAS. Determine analytically the limit along the path $\displaystyle x=y^2.$

Exercise $\PageIndex{12}$

1) [T]

a. Use a CAS to draw a contour map of $\displaystyle z=\sqrt{9−x^2−y^2}$.

b. What is the name of the geometric shape of the level curves?

c. Give the general equation of the level curves.

d. What is the maximum value of $\displaystyle z$?

e. What is the domain of the function?

f. What is the range of the function?

Answer

Solution:

a.

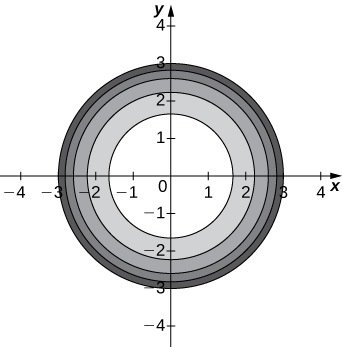
b. The level curves are circles centered at $\displaystyle (0,0)$ with radius $\displaystyle 9−c$. c. $\displaystyle x^2+y^2=9−c$ d. $\displaystyle z=3$ e. $\displaystyle {(x,y)∈R^2∣x^2+y^2≤9}$ f. $\displaystyle {z|0≤z≤3}$

Exercise $\PageIndex{13}$

1) True or False: If we evaluate $\displaystyle \lim_{(x,y)→(0,0)}f(x)$ along several paths and each time the limit is $\displaystyle 1$, we can conclude that $\displaystyle \lim_{(x,y)→(0,0)}f(x)=1.$

Exercise $\PageIndex{14}$

1) Use polar coordinates to find $\displaystyle \lim_{(x,y)→(0,0)}\frac{sin\sqrt{x^2+y^2}}{\sqrt{x^2+y^2}}.$ You can also find the limit using L’Hôpital’s rule.

Answer

Solution:$\displaystyle 1.0$

2) Use polar coordinates to find $\displaystyle \lim_{(x,y)→(0,0)}cos(x^2+y^2).$

3) Discuss the continuity of $\displaystyle f(g(x,y))$ where $\displaystyle f(t)=1/t$ and $\displaystyle g(x,y)=2x−5y.$

Answer

Solution:$\displaystyle f(g(x,y))$ is continuous at all points $\displaystyle (x,y)$ that are not on the line $\displaystyle 2x−5y=0.$

4) Given $\displaystyle f(x,y)=x^2−4y,$ find $\displaystyle \lim_{h→0}\frac{f(x+h,y)−f(x,y)}{h}.$

5) Given $\displaystyle f(x,y)=x^2−4y,$ find $\displaystyle \lim_{h→0}\frac{f(1+h,y)−f(1,y)}{h}$.

Answer

Solution:$\displaystyle 2.0$