6.4E: Exercises
- Last updated
- Nov 19, 2020
- Save as PDF
- Page ID
- 35383
( \newcommand{\kernel}{\mathrm{null}\,}\)
Exercise 6.4E.1
For the following exercises, use the information provided to solve the problem.
1) Let w(x,y,z)=xycosz, where x=t,y=t2, and z=arcsint. Find dwdt.
- Answer
-
dwdt=ycosz+xcosz(2t)−xysinz√1−t2
2) Let w(t,v)=etv where t=r+s and v=rs. Find ∂w∂r and ∂w∂s.
3) If w=5x2+2y2,x=−3s+t, and y=s−4t, find ∂w∂s and ∂w∂t.
- Answer
-
∂w∂s=−30x+4y,∂w∂t=10x−16y
4) If w=xy2,x=5cos(2t), and y=5sin(2t), find ∂w∂t.
5) If f(x,y)=xy,x=rcosθ, and y=rsinθ, find ∂f∂r and express the answer in terms of r and θ.
- Answer
-
∂f∂r=rsin(2θ)
6) Suppose f(x,y)=x+y,u=exsiny,x=t2 and y=πt, where x=rcosθ and y=rsinθ. Find ∂f∂θ.
Exercise 6.4E.2
For the following exercises, find dfdt using the chain rule and direct substitution.
7) f(x,y)=x2+y2,x=t,y=t2
- Answer
-
dfdt=2t+4t3
8) f(x,y)=√x2+y2,y=t2,x=t
9) f(x,y)=xy,x=1−√t,y=1+√t
- Answer
-
dfdt=−1
10) f(x,y)=xy,x=et,y=2et
11) f(x,y)=ln(x+y),x=et,y=et
- Answer
-
dfdt=1
12) f(x,y)=x4,x=t,y=t
Exercise 6.4E.3
13) Let w(x,y,z)=x2+y2+z2,x=cost,y=sint, and z=et. Express w as a function of t and find dwdt directly. Then, find dwdt using the chain rule.
- Answer
-
dwdt=2e2t in both cases
14) Let z=x2y, where x=t2 and y=t3. Find dzdt.
15) Let u=exsiny, where x=t2 and y=πt. Find dudt when x=ln2 and y=π4.
- Answer
-
2√2t+√2π=dudt
Exercise 6.4E.4
For the following exercises, find dydxusing partial derivatives.
16) sin(6x)+tan(8y)+5=0
17) x3+y2x−3=0
- Answer
-
dydx=−3x2+y22xy
18) sin(x+y)+cos(x−y)=4
19) x2−2xy+y4=4
- Answer
-
dydx=y−x−x+2y3
20) xey+yex−2x2y=0
21) x2/3+y2/3=a2/3
- Answer
-
dydx=−3√yx
22) xcos(xy)+ycosx=2
23) exy+yey=1
- Answer
-
dydx=−yexyxexy+ey(1+y)
24) x2y3+cosy=0
Exercise 6.4E.5
25) Find dzdt using the chain rule where z=3x2y3,x=t4, and y=t2.
- Answer
-
dzdt=42t13
26) Let z=3cosx−sin(xy),x=1t, and y=3t. Find dzdt.
27) Let z=e1−xy,x=t1/3, and y=t3. Find dzdt.
- Answer
-
dzdt=−103t7/3×e1−t10/3
28) Find dzdt by the chain rule where z=cosh2(xy),x=12t, and y=et.
29) Let z=xy,x=2cosu, and y=3sinv. Find ∂z∂u and ∂z∂v.
- Answer
-
∂z∂u=−2sinu3sinv and ∂z∂v=−2cosucosv3sin2v
30) Let z=ex2y, where x=√uv and y=1v. Find ∂z∂u and ∂z∂v.
31) If z=xyex/y,x=rcosθ, and y=rsinθ, find ∂z∂r and ∂z∂θ when r=2 and θ=π6.
- Answer
-
∂z∂r=√3e√3,∂z∂θ=(2−4√3)e√3
32) Find ∂w∂s if w=4x+y2+z3,x=ers2,y=ln(r+st), and z=rst2.
33) If w=sin(xyz),x=1−3t,y=e1−t, and z=4t, find ∂w∂t.
- Answer
-
∂w∂t=cos(xyz)×yz×(−3)−cos(xyz)xze1−t+cos(xyz)xy×4
Exercise 6.4E.6
For the following exercises, use this information: A function f(x,y) is said to be homogeneous of degree n if f(tx,ty)=tnf(x,y). For all homogeneous functions of degree n, the following equation is true: x∂f∂x+y∂f∂y=nf(x,y). Show that the given function is homogeneous and verify that x∂f∂x+y∂f∂y=nf(x,y).
34) f(x,y)=3x2+y2
35) f(x,y)=√x2+y2
- Answer
-
f(tx,ty)=√t2x2+t2y2=t1f(x,y),∂f∂y=x12(x2+y2)−1/2×2x+y12(x2+y2)−1/2×2y=1f(x,y)
36) f(x,y)=x2y−2y3
Exercise 6.4E.7
37) The volume of a right circular cylinder is given by V(x,y)=πx2y, where x is the radius of the cylinder and y is the cylinder height. Suppose x and y are functions of t given by x=12t and y=13t so that x and y are both increasing with time. How fast is the volume increasing when x=2 and y=5?
- Answer
-
34π3
38) The pressure P of a gas is related to the volume and temperature by the formula PV=kT, where temperature is expressed in kelvins. Express the pressure of the gas as a function of both V and T. Find dPdt when k=1,dVdt=2 cm3/min, dTdt=12 K/min, V=20cm3, and \displaystyle T=20°F.
39) The radius of a right circular cone is increasing at \displaystyle 3 cm/min whereas the height of the cone is decreasing at \displaystyle 2 cm/min. Find the rate of change of the volume of the cone when the radius is \displaystyle 13 cm and the height is \displaystyle 18 cm.
- Answer
-
\displaystyle \frac{dV}{dt}=\frac{1066π}{3}cm^3/min
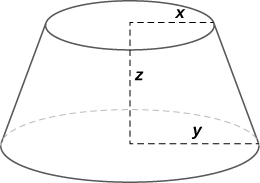
40) The volume of a frustum of a cone is given by the formula \displaystyle V=\frac{1}{3}πz(x^2+y^2+xy), where \displaystyle x is the radius of the smaller circle, \displaystyle y is the radius of the larger circle, and \displaystyle z is the height of the frustum (see figure). Find the rate of change of the volume of this frustum when \displaystyle x=10in.,y=12in., and \displaystyle z=18in.
41) A closed box is in the shape of a rectangular solid with dimensions \displaystyle x,y, and \displaystyle z. (Dimensions are in inches.) Suppose each dimension is changing at the rate of \displaystyle 0.5 in./min. Find the rate of change of the total surface area of the box when \displaystyle x=2in.,y=3in., and \displaystyle z=1in.
- Answer
-
\displaystyle \frac{dA}{dt}=12in.^2/min
42) The total resistance in a circuit that has three individual resistances represented by \displaystyle x,y, and \displaystyle z is given by the formula \displaystyle R(x,y,z)=\frac{xyz}{yz+xz+xy}. Suppose at a given time the \displaystyle x resistance is \displaystyle 100Ω, the \displaystyle y resistance is \displaystyle 200Ω, and the \displaystyle z resistance is \displaystyle 300Ω. Also, suppose the \displaystyle x resistance is changing at a rate of \displaystyle 2Ω/min, the \displaystyle y resistance is changing at the rate of \displaystyle 1Ω/min, and the \displaystyle z resistance has no change. Find the rate of change of the total resistance in this circuit at this time.
43) The temperature \displaystyle T at a point \displaystyle (x,y) is \displaystyle T(x,y) and is measured using the Celsius scale. A fly crawls so that its position after \displaystyle t seconds is given by \displaystyle x=\sqrt{1+t} and \displaystyle y=2+\frac{1}{3}t, where \displaystyle x and \displaystyle y are measured in centimeters. The temperature function satisfies \displaystyle T_x(2,3)=4 and \displaystyle T_y(2,3)=3. How fast is the temperature increasing on the fly’s path after \displaystyle 3 sec?
- Answer
-
\displaystyle 2°C/sec
44) The \displaystyle x and \displaystyle y components of a fluid moving in two dimensions are given by the following functions: \displaystyle u(x,y)=2y and \displaystyle v(x,y)=−2x; x≥0;y≥0. The speed of the fluid at the point \displaystyle (x,y) is \displaystyle s(x,y)=\sqrt{u(x,y)^2+v(x,y)^2}. Find \displaystyle \frac{∂s}{∂x} and \displaystyle \frac{∂s}{∂y} using the chain rule.
45) Let \displaystyle u=u(x,y,z), where \displaystyle x=x(w,t),y=y(w,t),z=z(w,t),w=w(r,s), and \displaystyle t=t(r,s). Use a tree diagram and the chain rule to find an expression for \displaystyle \frac{∂u}{∂r}.
- Answer
-
\displaystyle \frac{∂u}{∂r}=\frac{∂u}{∂x}(\frac{∂x}{∂w}\frac{∂w}{∂r}+\frac{∂x}{∂t}\frac{∂t}{∂r})+\frac{∂u}{∂y}(\frac{∂y}{∂w}\frac{∂w}{∂r}+\frac{∂y}{∂t}\frac{∂t}{∂r})+\frac{∂u}{∂z}(\frac{∂z}{∂w}\frac{∂w}{∂r}+\frac{∂z}{∂t}\frac{∂t}{∂r})

