6.1: Parametric equations - Tangent lines and arc length

In this section we examine parametric equations and their graphs. In the two-dimensional coordinate system, parametric equations are useful for describing curves that are not necessarily functions. The parameter is an independent variable that both $x$ and $y$ depend on, and as the parameter increases, the values of $x$ and $y$ trace out a path along a plane curve. For example, if the parameter is $t$ (a common choice), then $t$ might represent time. Then $x$ and $y$ are defined as functions of time, and $(x(t),y(t))$ can describe the position in the plane of a given object as it moves along a curved path.

Parametric Equations and Their Graphs

Consider the orbit of Earth around the Sun. Our year lasts approximately 365.25 days, but for this discussion we will use 365 days. On January 1 of each year, the physical location of Earth with respect to the Sun is nearly the same, except for leap years, when the lag introduced by the extra $\frac{1}{4}$ day of orbiting time is built into the calendar. We call January 1 “day 1” of the year. Then, for example, day 31 is January 31, day 59 is February 28, and so on.

The number of the day in a year can be considered a variable that determines Earth’s position in its orbit. As Earth revolves around the Sun, its physical location changes relative to the Sun. After one full year, we are back where we started, and a new year begins. According to Kepler’s laws of planetary motion, the shape of the orbit is elliptical, with the Sun at one focus of the ellipse. We study this idea in more detail in Conic Sections.

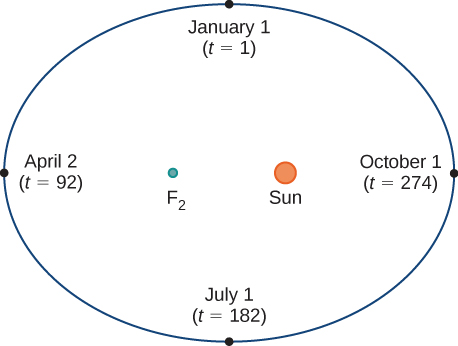
Figure $\PageIndex{1}$: Earth’s orbit around the Sun in one year.

Figure $\PageIndex{1}$ depicts Earth’s orbit around the Sun during one year. The point labeled $F_2$ is one of the foci of the ellipse; the other focus is occupied by the Sun. If we superimpose coordinate axes over this graph, then we can assign ordered pairs to each point on the ellipse (Figure $\PageIndex{2}$). Then each $x$ value on the graph is a value of position as a function of time, and each $y$ value is also a value of position as a function of time. Therefore, each point on the graph corresponds to a value of Earth’s position as a function of time.

Figure $\PageIndex{2}$: Coordinate axes superimposed on the orbit of Earth.

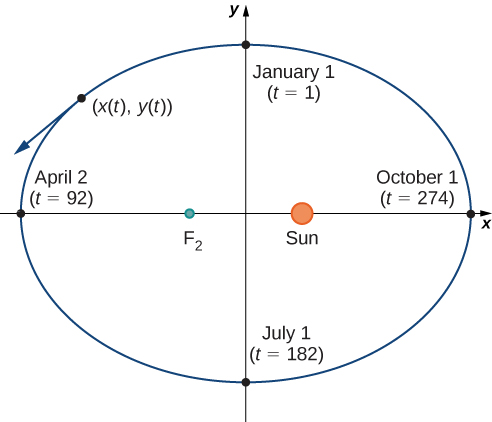
We can determine the functions for $x(t)$ and $y(t)$, thereby parameterizing the orbit of Earth around the Sun. The variable $t$ is called an independent parameter and, in this context, represents time relative to the beginning of each year.

A curve in the $(x,y)$ plane can be represented parametrically. The equations that are used to define the curve are called parametric equations.

Definition: Parametric Equations

If $x$ and $y$ are continuous functions of $t$ on an interval $I$, then the equations

$$x=x(t)$$

and

$$y=y(t)$$

are called parametric equations and $t$ is called the parameter. The set of points $(x,y)$ obtained as $t$ varies over the interval $I$ is called the graph of the parametric equations. The graph of parametric equations is called a parametric curve or plane curve, and is denoted by $C$.

Notice in this definition that x and y are used in two ways. The first is as functions of the independent variable $t$. As $t$ varies over the interval $I$, the functions $x(t)$ and $y(t)$ generate a set of ordered pairs $(x,y)$. This set of ordered pairs generates the graph of the parametric equations. In this second usage, to designate the ordered pairs, $x$ and $y$ are variables. It is important to distinguish the variables $x$ and $y$ from the functions $x(t)$ and $y(t)$.

Example $\PageIndex{1}$: Graphing a Parametrically Defined Curve

Sketch the curves described by the following parametric equations:

1. $x(t)=t−1, y(t)=2t+4,−3≤t≤2$
2. $x(t)=t^2−3,y(t)=2t+1,−2≤t≤3$
3. $x(t)=4 \cos t,y(t)=4 \sin t,0≤t≤2π$

Solution

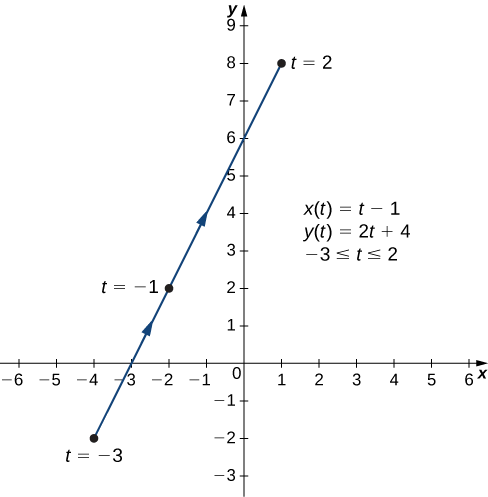
a. To create a graph of this curve, first set up a table of values. Since the independent variable in both $x(t)$ and $y(t)$ is $t$, let $t$ appear in the first column. Then $x(t)$ and $y(t)$ will appear in the second and third columns of the table.

$t$	$x(t)$	$y(t)$
−3	−4	−2
−2	−3	0
−1	−2	2
0	−1	4
1	0	6
2	1	8

The second and third columns in this table provide a set of points to be plotted. The graph of these points appears in Figure $\PageIndex{3}$. The arrows on the graph indicate the orientation of the graph, that is, the direction that a point moves on the graph as t varies from −3 to 2.

Figure $\PageIndex{3}$: Graph of the plane curve described by the parametric equations in part a.

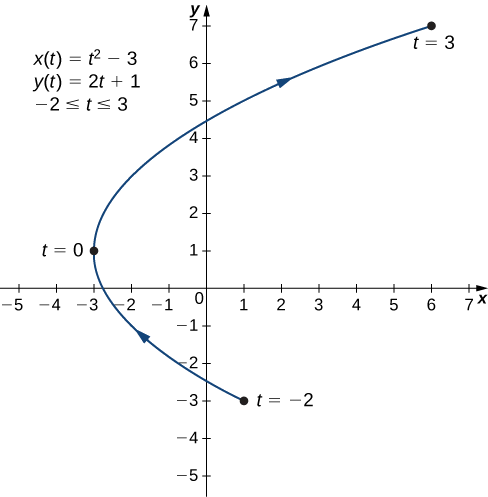
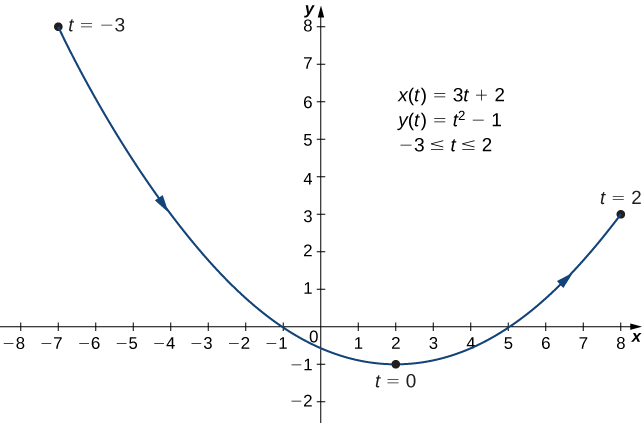
b. To create a graph of this curve, again set up a table of values.

$t$	$x(t)$	$y(t)$
−2	1	−3
−1	−2	−1
0	−3	1
1	−2	3
2	1	5
3	6	7

The second and third columns in this table give a set of points to be plotted (Figure $\PageIndex{4}$). The first point on the graph (corresponding to $t=−2$) has coordinates $(1,−3)$, and the last point (corresponding to $t=3$) has coordinates $(6,7)$. As t progresses from −2 to 3, the point on the curve travels along a parabola. The direction the point moves is again called the orientation and is indicated on the graph.

Figure $\PageIndex{4}$: Graph of the plane curve described by the parametric equations in part b.

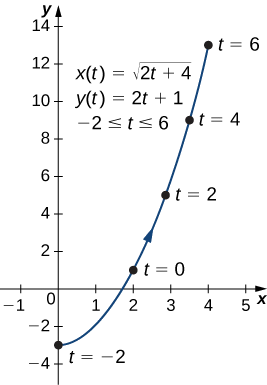
c. In this case, use multiples of $π/6$ for $t$ and create another table of values:

$t$	$x(t)$	$y(t)$	$t$	$x(t)$	$y(t)$
0	4	0	$\frac{7π}{6}$	−23√≈−3.5	2
$\frac{π}{6}$	$2\sqrt{3}≈3.5$	2	$\frac{4π}{3}$	−2	$−2\sqrt{3}≈−3.5$
$\frac{π}{3}$	2	$2\sqrt{3}≈3.5$	$\frac{3π}{2}$	0	−4
$\frac{π}{2}$	0	4	$\frac{5π}{3}$	2	$−2\sqrt{3}≈−3.5$
$\frac{2π}{3}$	−2	$2\sqrt{3}≈3.5$	$\frac{11π}{6}$	$2\sqrt{3}≈3.5$	2
$\frac{5π}{6}$	$−2\sqrt{3}≈−3.5$	2	$2π$	4	0
$π$	−4	0

The graph of this plane curve appears in the following graph.

Figure $\PageIndex{5}$: Graph of the plane curve described by the parametric equations in part c.

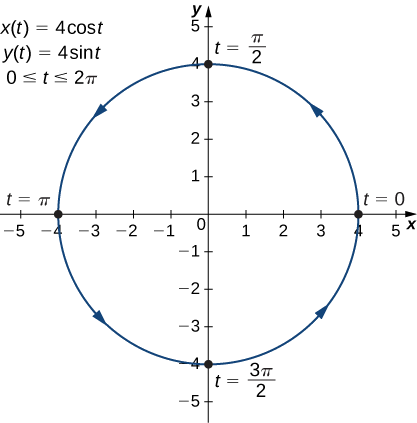
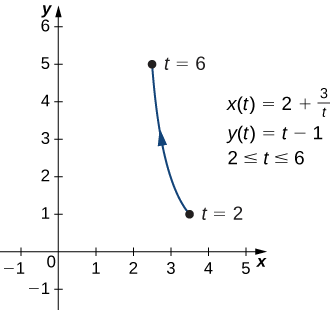
This is the graph of a circle with radius 4 centered at the origin, with a counterclockwise orientation. The starting point and ending points of the curve both have coordinates $(4,0)$.

Exercise $\PageIndex{1}$

Sketch the curve described by the parametric equations

$$x(t)=3t+2,y(t)=t^2−1,−3≤t≤2.$$

Hint

Make a table of values for $x(t)$ and $y(t)$ using t values from −3 to 2.

Answer

Eliminating the Parameter

To better understand the graph of a curve represented parametrically, it is useful to rewrite the two equations as a single equation relating the variables $x$ and $y$. Then we can apply any previous knowledge of equations of curves in the plane to identify the curve. For example, the equations describing the plane curve in Example $\PageIndex{1b}$ are

$$\begin{align} x(t)&=t^2−3 \label{x1} \\[5pt] y(t)&=2t+1 \label{y1} \end{align}$$

over the region $2 \le t \le 3.$

Solving Equation $\ref{y1}$ for $t$ gives

$$t=\dfrac{y−1}{2}.$$

This can be substituted into Equation $\ref{x1}$:

$$\begin{align} x&=\left(\dfrac{y−1}{2}\right)^2−3 \\[5pt] &=\dfrac{y^2−2y+1}{4}−3 \\[5pt]&=\dfrac{y^2−2y−11}{4}. \label{y2}\end{align}$$

Equation $\ref{y2}$ describes $x$ as a function of $y$. These steps give an example of eliminating the parameter. The graph of this function is a parabola opening to the right (Figure $\PageIndex{4}$). Recall that the plane curve started at $(1,−3)$ and ended at $(6,7)$. These terminations were due to the restriction on the parameter $t$.

Example $\PageIndex{2}$: Eliminating the Parameter

Eliminate the parameter for each of the plane curves described by the following parametric equations and describe the resulting graph.

1. $x(t)=\sqrt{2t+4},y(t)=2t+1,−2≤t≤6$
2. $x(t)=4\cos t,y(t)=3\sin t,0≤t≤2π$

Solution

a. To eliminate the parameter, we can solve either of the equations for $t$. For example, solving the first equation for $t$ gives

$$\begin{align*} x &=\sqrt{2t+4} \\[5pt] x^2 &=2t+4 \\[5pt] x^2−4 &=2t \\[5pt] t&=\dfrac{x^2−4}{2}. \end{align*}$$

Note that when we square both sides it is important to observe that $x≥0$. Substituting $t=\frac{x^2−4}{2}$ this into $y(t)$ yields

$$y(t)=2t+1$$

$$y=2(\frac{x^2−4}{2})+1$$

$$y=x^2−4+1$$

$$y=x^2−3.$$

This is the equation of a parabola opening upward. There is, however, a domain restriction because of the limits on the parameter $t$. When $t=−2, x=\sqrt{2(−2)+4}=0$, and when $t=6, x=\sqrt{2(6)+4}=4$. The graph of this plane curve follows.

Figure $\PageIndex{6}$: Graph of the plane curve described by the parametric equations in part a.

b. Sometimes it is necessary to be a bit creative in eliminating the parameter. The parametric equations for this example are

$$x(t)=4 \cos t$$

and

$$y(t)=3 \sin t$$

Solving either equation for t directly is not advisable because sine and cosine are not one-to-one functions. However, dividing the first equation by 4 and the second equation by 3 (and suppressing the t) gives us

$$\cos t=\dfrac{x}{4}$$

and

$$\sin t=\dfrac{y}{3}.$$

Now use the Pythagorean identity $\cos^2t+\sin^2t=1$ and replace the expressions for $\sin t$ and $\cos t$ with the equivalent expressions in terms of x and y. This gives

$$(\dfrac{x}{4})^2+(\dfrac{y}{3})^2=1$$

$$\dfrac{x^2}{16}+\dfrac{y^2}{9}=1.$$

This is the equation of a horizontal ellipse centered at the origin, with semi-major axis 4 and semi-minor axis 3 as shown in the following graph.

Figure $\PageIndex{7}$: Graph of the plane curve described by the parametric equations in part b.

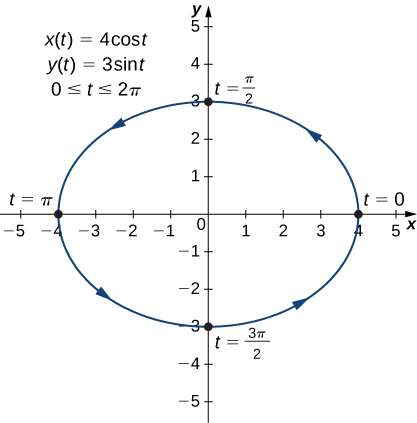
As t progresses from $0$ to $2π$, a point on the curve traverses the ellipse once, in a counterclockwise direction. Recall from the section opener that the orbit of Earth around the Sun is also elliptical. This is a perfect example of using parameterized curves to model a real-world phenomenon.

Exercise $\PageIndex{2}$

Eliminate the parameter for the plane curve defined by the following parametric equations and describe the resulting graph.

$$x(t)=2+\dfrac{3}{t},y(t)=t−1,2≤t≤6$$

Hint

Solve one of the equations for t and substitute into the other equation.

Answer

$x=2+\frac{3}{y+1},$ or $y=−1+\frac{3}{x−2}$. This equation describes a portion of a rectangular hyperbola centered at $(2,−1)$.

So far we have seen the method of eliminating the parameter, assuming we know a set of parametric equations that describe a plane curve. What if we would like to start with the equation of a curve and determine a pair of parametric equations for that curve? This is certainly possible, and in fact it is possible to do so in many different ways for a given curve. The process is known as parameterization of a curve.

Example $\PageIndex{3}$: Parameterizing a Curve

Find two different pairs of parametric equations to represent the graph of $y=2x^2−3$.

Solution

First, it is always possible to parameterize a curve by defining $x(t)=t$, then replacing x with t in the equation for $y(t)$. This gives the parameterization

$$x(t)=t, y(t)=2t^2−3.$$

Since there is no restriction on the domain in the original graph, there is no restriction on the values of $t$.

We have complete freedom in the choice for the second parameterization. For example, we can choose $x(t)=3t−2$. The only thing we need to check is that there are no restrictions imposed on x; that is, the range of $x(t)$ is all real numbers. This is the case for $x(t)=3t−2$. Now since $y=2x^2−3$, we can substitute $x(t)=3t−2$ for x. This gives

$$y(t)=2(3t−2)^2−2=2(9t^2−12t+4)−2=18t^2−24t+8−2=18t^2−24t+6.$$

Therefore, a second parameterization of the curve can be written as

$x(t)=3t−2$ and \(y(t)=18t^2−24t+6.\]

Exercise $\PageIndex{3}$

Find two different sets of parametric equations to represent the graph of $y=x^2+2x$.

Hint

Follow the steps in Example. Remember we have freedom in choosing the parameterization for $x(t)$.

Answer

One possibility is $x(t)=t,y(t)=t^2+2t.$ Another possibility is $x(t)=2t−3,y(t)=(2t−3)^2+2(2t−3)=4t^2−8t+3.$ There are, in fact, an infinite number of possibilities.

Cycloids and Other Parametric Curves

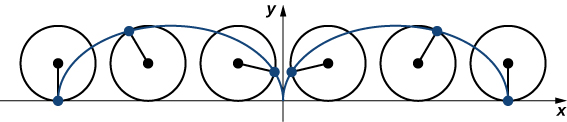
Imagine going on a bicycle ride through the country. The tires stay in contact with the road and rotate in a predictable pattern. Now suppose a very determined ant is tired after a long day and wants to get home. So he hangs onto the side of the tire and gets a free ride. The path that this ant travels down a straight road is called a cycloid (Figure $\PageIndex{8}$). A cycloid generated by a circle (or bicycle wheel) of radius a is given by the parametric equations

$$x(t)=a(t−\sin t),y(t)=a(1−\cos t).$$

To see why this is true, consider the path that the center of the wheel takes. The center moves along the x-axis at a constant height equal to the radius of the wheel. If the radius is a, then the coordinates of the center can be given by the equations

$$x(t)=at,y(t)=a$$

for any value of $t$. Next, consider the ant, which rotates around the center along a circular path. If the bicycle is moving from left to right then the wheels are rotating in a clockwise direction. A possible parameterization of the circular motion of the ant (relative to the center of the wheel) is given by

$$\begin{align*} x(t)&=−a \sin t \\[5pt] y(t)&=−a\cos t.\end{align*}$$

(The negative sign is needed to reverse the orientation of the curve. If the negative sign were not there, we would have to imagine the wheel rotating counterclockwise.) Adding these equations together gives the equations for the cycloid.

$$\begin{align*} x(t)&=a(t−\sin t) \\[5pt] y(t) &=a(1−\cos t ) \end{align*}$$

Figure $\PageIndex{8}$: A wheel traveling along a road without slipping; the point on the edge of the wheel traces out a cycloid.

Now suppose that the bicycle wheel doesn’t travel along a straight road but instead moves along the inside of a larger wheel, as in Figure $\PageIndex{9}$. In this graph, the green circle is traveling around the blue circle in a counterclockwise direction. A point on the edge of the green circle traces out the red graph, which is called a hypocycloid.

Figure $\PageIndex{9}$: Graph of the hypocycloid described by the parametric equations shown.

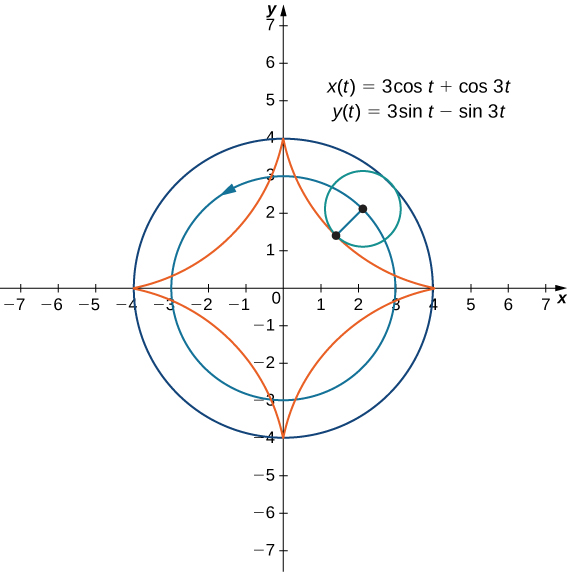
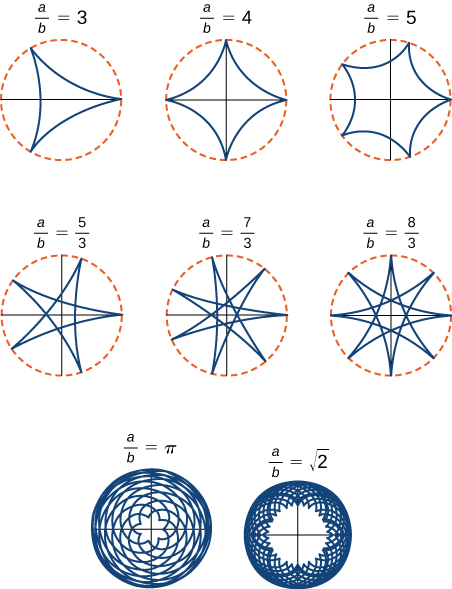
The general parametric equations for a hypocycloid are

$$x(t)=(a−b) \cos t+b \cos (\dfrac{a−b}{b})t$$

$$y(t)=(a−b) \sin t−b \sin (\dfrac{a−b}{b})t.$$

These equations are a bit more complicated, but the derivation is somewhat similar to the equations for the cycloid. In this case we assume the radius of the larger circle is a and the radius of the smaller circle is b. Then the center of the wheel travels along a circle of radius $a−b.$ This fact explains the first term in each equation above. The period of the second trigonometric function in both $x(t)$ and $y(t)$ is equal to $\frac{2πb}{a−b}$.

The ratio $\frac{a}{b}$ is related to the number of cusps on the graph (cusps are the corners or pointed ends of the graph), as illustrated in Figure $\PageIndex{10}$. This ratio can lead to some very interesting graphs, depending on whether or not the ratio is rational. Figure corresponds to $a=4$ and $b=1$. The result is a hypocycloid with four cusps. Figure shows some other possibilities. The last two hypocycloids have irrational values for $\frac{a}{b}$. In these cases the hypocycloids have an infinite number of cusps, so they never return to their starting point. These are examples of what are known as space-filling curves.

Figure $\PageIndex{10}$: Graph of various hypocycloids corresponding to different values of $a/b$.

The Witch of Agnesi

Many plane curves in mathematics are named after the people who first investigated them, like the folium of Descartes or the spiral of Archimedes. However, perhaps the strangest name for a curve is the witch of Agnesi. Why a witch?

Maria Gaetana Agnesi (1718–1799) was one of the few recognized women mathematicians of eighteenth-century Italy. She wrote a popular book on analytic geometry, published in 1748, which included an interesting curve that had been studied by Fermat in 1630. The mathematician Guido Grandi showed in 1703 how to construct this curve, which he later called the “versoria,” a Latin term for a rope used in sailing. Agnesi used the Italian term for this rope, “versiera,” but in Latin, this same word means a “female goblin.” When Agnesi’s book was translated into English in 1801, the translator used the term “witch” for the curve, instead of rope. The name “witch of Agnesi” has stuck ever since.

The witch of Agnesi is a curve defined as follows: Start with a circle of radius a so that the points $(0,0)$ and $(0,2a)$ are points on the circle (Figure $\PageIndex{11}$). Let O denote the origin. Choose any other point A on the circle, and draw the secant line OA. Let B denote the point at which the line OA intersects the horizontal line through $(0,2a)$. The vertical line through B intersects the horizontal line through A at the point P. As the point A varies, the path that the point P travels is the witch of Agnesi curve for the given circle.

Witch of Agnesi curves have applications in physics, including modeling water waves and distributions of spectral lines. In probability theory, the curve describes the probability density function of the Cauchy distribution. In this project you will parameterize these curves.

Figure $\PageIndex{11}$: As the point A moves around the circle, the point P traces out the witch of Agnesi curve for the given circle.

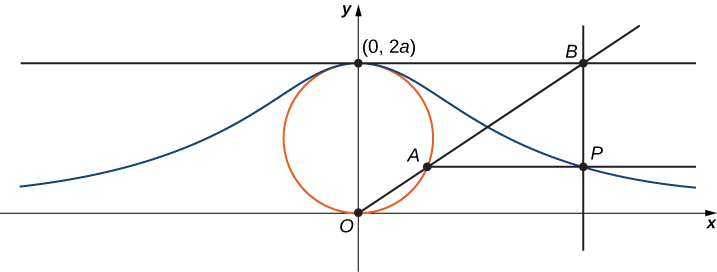
1. On the figure, label the following points, lengths, and angle:

a. C is the point on the x-axis with the same x-coordinate as A.

b. x is the x-coordinate of P, and y is the y-coordinate of P.

c. E is the point $(0,a)$.

d. F is the point on the line segment OA such that the line segment EF is perpendicular to the line segment OA.

e. b is the distance from O to F.

f. c is the distance from F to A.

g. d is the distance from O to B.

h. $θ$ is the measure of angle $∠COA$.

The goal of this project is to parameterize the witch using $θ$ as a parameter. To do this, write equations for x and y in terms of only $θ$.

2. Show that $d=\frac{2a}{sinθ}$.

3. Note that $x=dcosθ$. Show that $x=2acotθ$. When you do this, you will have parameterized the x-coordinate of the curve with respect to $θ$. If you can get a similar equation for y, you will have parameterized the curve.

4. In terms of $θ$, what is the angle $∠EOA$?

5. Show that $b+c=2acos(\frac{π}{2}−θ)$.

6. Show that $y=2acos(\frac{π}{2}−θ)sinθ$.

7. Show that $y=2asin^2θ$. You have now parameterized the y-coordinate of the curve with respect to $θ$.

8. Conclude that a parameterization of the given witch curve is

$$x=2a\cot θ,y=2a \sin^2θ,−∞<θ<∞.$$

9. Use your parameterization to show that the given witch curve is the graph of the function $f(x)=\frac{8a^3}{x^2+4a^2}$.

Travels with My Ant: The Curtate and Prolate Cycloids

Earlier in this section, we looked at the parametric equations for a cycloid, which is the path a point on the edge of a wheel traces as the wheel rolls along a straight path. In this project we look at two different variations of the cycloid, called the curtate and prolate cycloids.

First, let’s revisit the derivation of the parametric equations for a cycloid. Recall that we considered a tenacious ant trying to get home by hanging onto the edge of a bicycle tire. We have assumed the ant climbed onto the tire at the very edge, where the tire touches the ground. As the wheel rolls, the ant moves with the edge of the tire (Figure).

As we have discussed, we have a lot of flexibility when parameterizing a curve. In this case we let our parameter t represent the angle the tire has rotated through. Looking at Figure $\PageIndex{12}$, we see that after the tire has rotated through an angle of t, the position of the center of the wheel, $C=(x_C,y_C)$, is given by

$x_C=at$ and $y_C=a$.

Furthermore, letting $A=(x_A,y_A)$ denote the position of the ant, we note that

$x_C−x_A=asint$ and $y_C−y_A=a \cos t$

Then

$$x_A=x_C−a\sin t=at−a\sin t=a(t−sint)$$

$$y_A=y_C−a\cos t=a−a\cos t=a(1−cost).$$

Figure $\PageIndex{12}$: (a) The ant clings to the edge of the bicycle tire as the tire rolls along the ground. (b) Using geometry to determine the position of the ant after the tire has rotated through an angle of $t$.

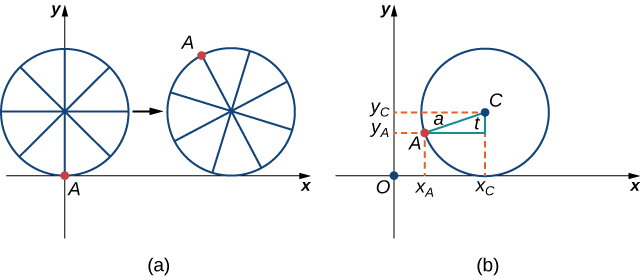
Note that these are the same parametric representations we had before, but we have now assigned a physical meaning to the parametric variable $t$.

After a while the ant is getting dizzy from going round and round on the edge of the tire. So he climbs up one of the spokes toward the center of the wheel. By climbing toward the center of the wheel, the ant has changed his path of motion. The new path has less up-and-down motion and is called a curtate cycloid (Figure $\PageIndex{13}$). As shown in the figure, we let b denote the distance along the spoke from the center of the wheel to the ant. As before, we let t represent the angle the tire has rotated through. Additionally, we let $C=(x_C,y_C)$ represent the position of the center of the wheel and $A=(x_A,y_A)$ represent the position of the ant.

Figure $\PageIndex{13}$: (a) The ant climbs up one of the spokes toward the center of the wheel. (b) The ant’s path of motion after he climbs closer to the center of the wheel. This is called a curtate cycloid. (c) The new setup, now that the ant has moved closer to the center of the wheel.

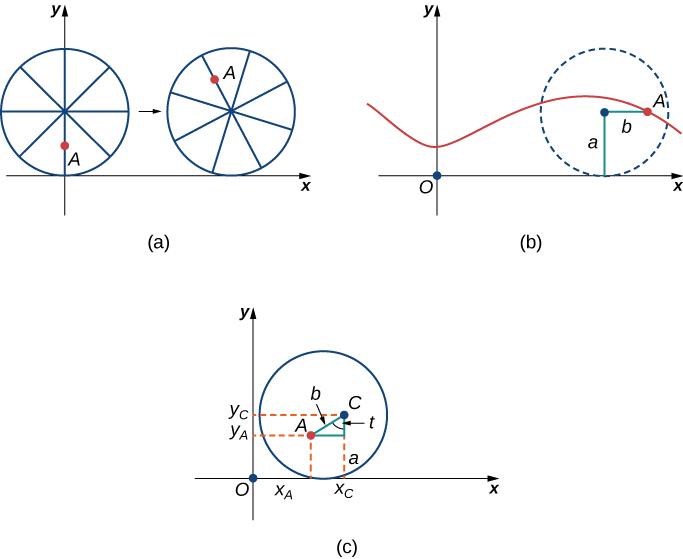
1. What is the position of the center of the wheel after the tire has rotated through an angle of $t$?

2. Use geometry to find expressions for $x_C−x_A$ and for $y_C−y_A$.

3. On the basis of your answers to parts 1 and 2, what are the parametric equations representing the curtate cycloid?

Once the ant’s head clears, he realizes that the bicyclist has made a turn, and is now traveling away from his home. So he drops off the bicycle tire and looks around. Fortunately, there is a set of train tracks nearby, headed back in the right direction. So the ant heads over to the train tracks to wait. After a while, a train goes by, heading in the right direction, and he manages to jump up and just catch the edge of the train wheel (without getting squished!).

The ant is still worried about getting dizzy, but the train wheel is slippery and has no spokes to climb, so he decides to just hang on to the edge of the wheel and hope for the best. Now, train wheels have a flange to keep the wheel running on the tracks. So, in this case, since the ant is hanging on to the very edge of the flange, the distance from the center of the wheel to the ant is actually greater than the radius of the wheel (Figure).

The setup here is essentially the same as when the ant climbed up the spoke on the bicycle wheel. We let b denote the distance from the center of the wheel to the ant, and we let t represent the angle the tire has rotated through. Additionally, we let $C=(x_C,y_C)$ represent the position of the center of the wheel and $A=(x_A,y_A)$ represent the position of the ant (Figure $\PageIndex{14}$).

When the distance from the center of the wheel to the ant is greater than the radius of the wheel, his path of motion is called a prolate cycloid. A graph of a prolate cycloid is shown in the figure.

Figure $\PageIndex{14}$: (a) The ant is hanging onto the flange of the train wheel. (b) The new setup, now that the ant has jumped onto the train wheel. (c) The ant travels along a prolate cycloid.

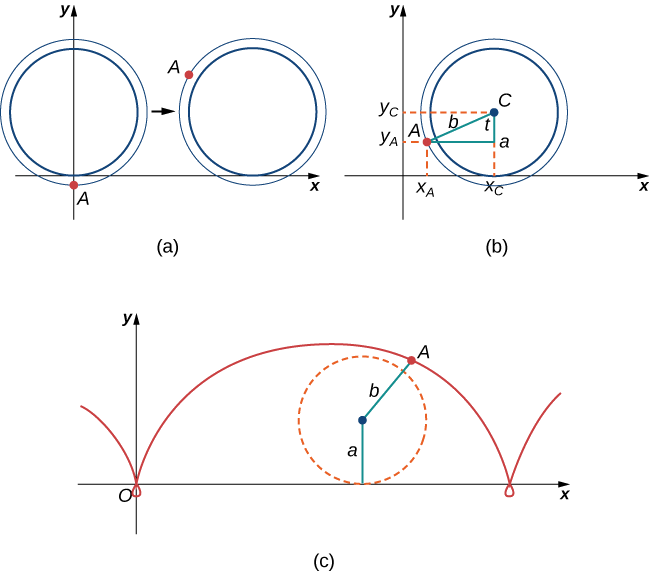
4. Using the same approach you used in parts 1– 3, find the parametric equations for the path of motion of the ant.

5. What do you notice about your answer to part 3 and your answer to part 4?

Notice that the ant is actually traveling backward at times (the “loops” in the graph), even though the train continues to move forward. He is probably going to be really dizzy by the time he gets home!

Key Concepts

• Parametric equations provide a convenient way to describe a curve. A parameter can represent time or some other meaningful quantity.
• It is often possible to eliminate the parameter in a parameterized curve to obtain a function or relation describing that curve.
• There is always more than one way to parameterize a curve.
• Parametric equations can describe complicated curves that are difficult or perhaps impossible to describe using rectangular coordinates.

Glossary

cycloid

the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line without slippage

cusp

a pointed end or part where two curves meet

orientation

the direction that a point moves on a graph as the parameter increases

parameter

an independent variable that both x and y depend on in a parametric curve; usually represented by the variable t

parametric curve

the graph of the parametric equations $x(t)$ and $y(t)$ over an interval $a≤t≤b$ combined with the equations

parametric equations

the equations $x=x(t)$ and $y=y(t)$ that define a parametric curve

parameterization of a curve

rewriting the equation of a curve defined by a function $y=f(x)$ as parametric equations

Contributors and Attributions

• Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.