Test 1(Mock Exam)

Last updated
Save as PDF

Page ID: 26374

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

These mock exams are provided to help you prepare for Term/Final tests. The best way to use these practice tests is to try the problems as if you were taking the test. Please don't look at the solution until you have attempted the question(s). Only reading through the answers or studying them, will typically not be helpful in preparing since it is too easy to convince yourself that you understand it.

Exercise $\PageIndex{1}$

Find the volume of the solid that results in when the region enclosed by $x=y^2$ and $2y=2x$ is revolved about the line $x=-1.$

Answer: $\dfrac{7\pi}{15} \mbox{ unit}^3$

Solution

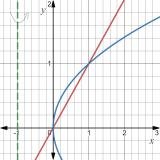
$Test1_1_PT.jpg$

Point of intersections, we solve $x=y^2$ and $2x=2y.$

Now, $y^2=y \implies y=0,1.$

Method I:

Using Disk/Washer method,

\begin{align*} V &=\pi \int_0^1 \left( (y+1)^2-(y^2+1)^2\right) dy \\ &= \pi \int_0^1 (2y-y^2-y^4) dy \\& =\dfrac{7\pi}{15} \mbox{ unit}^3. \end{align*}

Method II:

Using Shell method, \begin{align*}V &=2\pi \int_0^1 (x+1)\left(\sqrt{x}-x \right) dx\\ &=2\pi \int_0^1 \left(x^{3/2}-x^2+x^{1/2}-x \right) dx \\&=2\pi \left(\dfrac{2}{5}x^{5/2}-\dfrac{1}{3}x^3+\dfrac{2}{3}x^{3/2}-\dfrac{1}{2}x^2 \right)\left|_0^1 \right.\\ & =\dfrac{7\pi}{15} \mbox{ unit}^3.\end{align*}

Exercise $\PageIndex{2}$

Use cylindrical shells to find the volume generated when the region between the two curves $y=\sqrt{x} , y=0, x=1,$ and $x=4$ is revolved about the $y-$axis.

Answer: $\dfrac{62\pi}{5} \mbox{ unit}^3.$

Solution: $$V=2 \pi \int_1^4 x(\sqrt{x}) dx=2 \pi \int_1^4 x^{\frac{3}{2}} dx= \dfrac{4 \pi}{5} x^{\frac{5}{2}}|_1^4= \dfrac{62\pi}{5} \mbox{ unit}^3.$$

Exercise $\PageIndex{3}$

Find the exact arc length of the curve $ x=\frac{1}{8}y^4+\frac{1}{4}y^{-2}$ from $y=4$ to $y=9.$

Answer: $\dfrac{5516}{7}\mbox{ unit}$

Solution

$$g^{\prime}(y)=\dfrac{1}{2}y^3- \dfrac{1}{2}y^{-3},$$ therefore, $$1+(g^{\prime}(y)^2=1+\left(\dfrac{1}{2}y^3- \dfrac{1}{2}y^{-3}\right)^2=1+\dfrac{1}{2^2}y^6- 2 \left(\dfrac{1}{2} y^3 \right) \left( \dfrac{1}{2}y^{-3} \right)+ \dfrac{1}{2^2}y^{-6}= 1+\dfrac{1}{2^2}y^6- \dfrac{1}{2} + \dfrac{1}{2^2}y^{-6}=\dfrac{1}{2^2}y^6+ \dfrac{1}{2}+ \dfrac{1}{2^2}y^{-6} =\left(\dfrac{1}{2}y^3+ \dfrac{1}{2}y^{-3}\right)^2.$$

Hence $$\mbox{Arc length}=\int_4^9 \sqrt{\left(\dfrac{1}{2}y^3+ \dfrac{1}{2}y^{-3}\right)^2}dy= \int_4^9 \left(\dfrac{1}{2}y^3+ \dfrac{1}{2}y^{-3}\right) dy= \left(\dfrac{1}{8}y^4+ \dfrac{-1}{4}y^{-2}\right)|_4^9= \dfrac{5516}{7}\mbox{ unit}.$$

Exercise $\PageIndex{4}$

Find the area of the surface generated by revolving

$y=\dfrac{e^x+e^{-x}}{2}, 1\leq x\leq 4,$ about the x-axis.

Answer: $\dfrac{\pi}{2}( (e^{8}+6- e^{-8}-e^{2}+ e^{-2})) \text{units}$

Solution

We have $ f^{\prime}(x)=\dfrac{1}{2}(e^x- e^{-x}),$ so $ [f^{\prime}(x)]^2=\left( \dfrac{1}{2}(e^x- e^{-x}) \right)^2= \dfrac{1}{4} (e^{2x}-2 + e^{-2x}).$

Therefore, $ 1+[f^{\prime}(x)]^2 = 1+ \dfrac{1}{4} (e^{2x}-2 + e^{-2x}) = \dfrac{1}{4} (4+e^{2x}-2 + e^{-2x})= \dfrac{1}{4} (e^{2x} +2 + e^{-2x}) = \left(\dfrac{1}{2}(e^x+e^{-x})\right)^2 .$

\begin{align*} \text{Surface area} &=\int^b_a 2\pi f(x) \sqrt{1+[f^{\prime}(x)]^2}dx \\[5pt] &= \int^{4}_{1} 2\pi \left( \dfrac{1}{2}(e^x+e^{-x}) \right)^2 dx\\[5pt] &= \int^{4}_{1} \pi \dfrac{1}{2}(e^{2x}+2+e^{-2x}) dx\\[5pt] &= \dfrac{\pi}{2} (\dfrac{e^{2x}}{2}+2x- \dfrac{e^{-2x}}{2})|^{4}_{1} \\[5pt] &= \dfrac{\pi}{4}( (e^{8}+16- e^{-8})- (e^{2}+4- e^{-2})) \\[5pt] &= \dfrac{\pi}{4}( (e^{8}+10- e^{-8}-e^{2}+ e^{-2})) \text{units} \end{align*}

Exercise $\PageIndex{5}$

Calculate the following integrals:

$\displaystyle \int_{1/2}^{\sqrt{3}/2} \sin^{-1}x\ dx$
$\displaystyle \int \sin^2(x) \cos^4(x)\, dx$
$\displaystyle \int \frac{2}{x^2\sqrt{2x^2+50}} \, dx $

Answer

$\dfrac{\sqrt{3} \pi}{6}-\dfrac{\pi}{12}+\dfrac{1-\sqrt{3}}{2}$

$\dfrac{x}{16}-\dfrac{1}{64}\sin(4x)+\dfrac{1}{48}\sin^3(2x) +C$

$\displaystyle \int \frac{2}{x^2\sqrt{2x^2+50}} \ dx = \displaystyle \frac{ -\sqrt{2}}{25} \frac{ \sqrt{x^2+25}}{x} +C.$

Solution

1. Using integration by parts, let $u=\sin^{-1}(x)$ and $dv=dx.$ Then $du=\dfrac{1}{\sqrt{1-x^2}}$ and $v=x$. Therefore

\begin{align*}\displaystyle \int_{1/2}^{\sqrt{3}/2} \sin^{-1}x\ dx & = x\sin^{-1}(x) |_{1/2}^{\sqrt{3}/2}- \int_{1/2}^{\sqrt{3}/2} \dfrac{x}{\sqrt{1-x^2}}dx \\&= ( x\sin^{-1}(x)+\sqrt{1-x^2}) |_{1/2}^{\sqrt{3}/2}\\&=\left((\sqrt{3}/2) sin^{-1}(\sqrt{3}/2)+ \sqrt{1-\sqrt{3}/2} \right) -\left((1/2) sin^{-1}(1/2)+ \sqrt{1-1/2} \right) \\&= \dfrac{\sqrt{3} \pi}{6}-\dfrac{\pi}{12}+\dfrac{1-\sqrt{3}}{2}. \end{align*}

\begin{align*}\displaystyle \int \sin^2(x) \cos^4(x)\, dx &= \dfrac{1}{8} \int (1-\cos(2x))(1+\cos(2x))^2 dx\\&=\dfrac{1}{8} \int (1-\cos^2(2x))(1+\cos(2x)) dx\\&=\dfrac{1}{8} \int \sin^2(2x)dx+\dfrac{1}{8} \int \sin^2(2x) \cos(2x)dx\\&= \dfrac{1}{8} \int(1-\cos(4x)) dx+ \dfrac{1}{48}\sin^3(2x)\\&=\dfrac{x}{16}-\dfrac{1}{64}\sin(4x)+\dfrac{1}{48}\sin^3(2x) +C \end{align*}

Let $x=5 \tan(\theta)$, then $ dx= 5 \sec^2({\theta}) d\theta$ and $ x^2+25=25 \sec^2(\theta).$

\begin{align*}\displaystyle \int \frac{2}{x^2\sqrt{2x^2+50}} \ dx & = \displaystyle \frac{2}{\sqrt{2}} \int \frac{1}{x^2\sqrt{x^2+25}} dx \\&= \displaystyle \frac{ \sqrt{2}}{25} \int \frac{ \sec^2({\theta})}{ \tan^2(\theta)\sec(\theta)} d\theta \\ &= \displaystyle \frac{ \sqrt{2}}{25} \int \frac{ \sec({\theta})}{ \tan^2(\theta)} d\theta \\& = \displaystyle \frac{ \sqrt{2}}{25} \int \csc({\theta}) \cot(\theta) d\theta\\& = \displaystyle \frac{ -\sqrt{2}}{25} \csc({\theta}) +C .\end{align*}

Since $\tan(\theta)= \displaystyle \frac{x}{5}, \sin(\theta)= \displaystyle \frac{x}{\sqrt{x^2+25}}. $

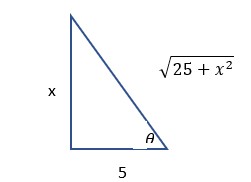
$t2q1.1.jpg$

Therefore,

$\displaystyle \int \frac{2}{x^2\sqrt{2x^2+50}} \ dx = \displaystyle \frac{ -\sqrt{2}}{25} \frac{ \sqrt{x^2+25}}{x} +C.$

Exercise $\PageIndex{6}$

Determine if the following improper integral diverges or converges. If it converges, determine what number it converges to.

\[\int_{e}^{\infty} \frac{dx}{x\ln^3(x)} \nonumber\]

Answer: The integral converges to $ \displaystyle \frac{1}{2}.$

Solution

\begin{align*}\displaystyle \int_{e}^{\infty} \frac{dx}{x\ln^3(x)} & = \lim_{t \to \infty}\displaystyle \int_{e}^{t} \frac{dx}{x\ln^3(x)} \end{align*}

Let $u=ln(x),$ then $du=\displaystyle \frac{1}{x}dx.$ Then

\begin{align*}\displaystyle \int_{e}^{\infty} \frac{dx}{x\ln^3(x)} & = \lim_{t \to \infty}\displaystyle \int_{e}^{t} \frac{dx}{x\ln^3(x)}\\&= \lim_{t \to \infty}\displaystyle \int_{x=e}^{x=t} \frac{du}{u^3} \\&= \lim_{t \to \infty}\displaystyle \int_{x=e}^{x=t} u^{-3}du\\&= \lim_{t \to \infty}\displaystyle \frac{u^{-2}} {-2}|_{x=e}^{x=t}\\&= \lim_{t \to \infty}\displaystyle \frac{-1}{2ln(x)^2}|_{x=e}^{x=t}\\&= \lim_{t \to \infty}\displaystyle \left( \frac{-1}{2ln(t)^2}+\frac{1}{2ln(e)^2} \right)\\&=0+ \displaystyle \frac{1}{2}= \displaystyle \frac{1}{2}.\end{align*}

Hence the integral converges to $ \displaystyle \frac{1}{2}.$