5.4E:Exercises

Exercise \(\PageIndex{1}\)

1) Given \(\vec{r(t)}=(3t^2−2)\hat{\mathbf i}+(2t−sin(t))\hat{\mathbf j}\), find the velocity of a particle moving along this curve.

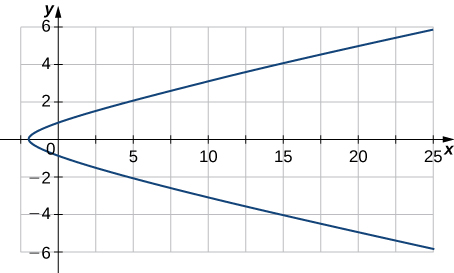
2) Given \(\vec{r(t)}=(3t^2−2)\hat{\mathbf i}+(2t−sin(t))\hat{\mathbf j}\), find the acceleration vector of a particle moving along the curve in the preceding exercise.

Answer

1) \(\vec{v(t)}=(6t)\hat{\mathbf i}+(2−cos(t))\hat{\mathbf j}\)

Exercise \(\PageIndex{2}\)

Given the following position functions, find the velocity, acceleration, and speed in terms of the parameter \(t.\)

1) \(\vec{r(t)}=⟨3cost, 3sint, t^2⟩\)

2) \(\vec{r(t)}=e^{−t} \hat{\mathbf i}+t^2\hat{\mathbf j}+tan(t) \hat{\mathbf k}\)

3) \(\vec{r(t)}=2cost \hat{\mathbf j}+3sint \hat{\mathbf k}.\) The graph is shown here:

4) \(\vec{r(t)}=⟨t^2−1,t⟩\)

5) \( \vec{r(t)}=⟨e^t,e^{−t}⟩\)

6) \(\vec{r(t)}=⟨sint,t,cost⟩.\) The graph is shown here:

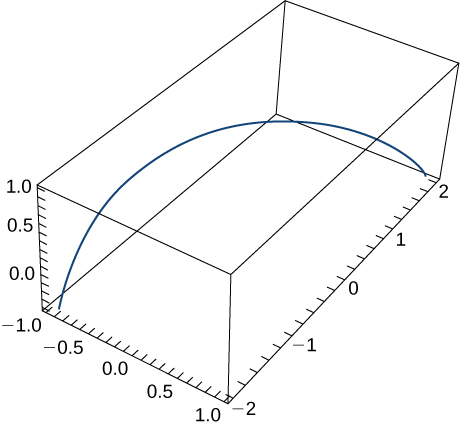
Answer

1) \(\vec{v(t)}=⟨−3sint,3cost,2t⟩\),\(a(t)=⟨−3cost,−3sint,2⟩\), speed \(= \sqrt{9+4t^2}\)

3)\(\vec{v(t)}=−2sint\hat{\mathbf j}+3costk, a(t)=−2cost\hat{\mathbf j}−3sint\hat{\mathbf k}\), speed \(= \sqrt{4sin^2(t)+9cos^2(t)\)

5) \(\vec{v(t)}=e^t\hat{\mathbf i}−e^{−t}\hat{\mathbf j}, a(t)=e^t\hat{\mathbf i}+e^{−t}\hat{\mathbf j}\), speed \(= \sqrt{ e^{2t}+e^{−2t}}\)

Exercise \(\PageIndex{3}\)

1) The position function of an object is given by \(\vec{r(t)}=⟨t^2,5t,t^2−16t⟩.\) At what time is the speed a minimum?

2) Let \(\vec{r(t)}=rcosh(ωt)\hat{\mathbf i}+rsinh(ωt)\hat{\mathbf j}.\) Find the velocity and acceleration vectors. Further, show that the acceleration is proportional to \(\vec{r(t)}.\)

3) Consider the motion of a point on the circumference of a rolling circle. As the circle rolls, it generates the cycloid \(\vec{r(t)}=(ωt−sin(ωt))\hat{\mathbf i}+(1−cos(ωt))\hat{\mathbf j},\) where \(ω\) is the angular velocity of the circle and \(b\) is the radius of the circle.

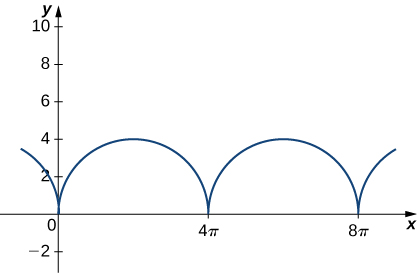
Find the equations for the velocity, acceleration, and speed of the particle at any time.

Answer

1) \(t=4\)

3) \(\vec{v(t)}=(ω−ωcos(ωt))\hat{\mathbf i}+(ωsin(ωt))\hat{\mathbf j}, a(t)=(ω^2sin(ωt))i+(ω^2cos(ωt))\hat{\mathbf j},\)

speed=\(\sqrt{ω^2−2ω^2cos(ωt)+ω^2cos^2(ωt)+ω^2sin^2(ωt)}= \sqrt{2ω^2(1−cos(ωt)}\).

Exercise \(\PageIndex{4}\)

A person on a hang glider is spiralling upward as a result of the rapidly rising air on a path having position vector \(\vec{r(t)}=(3cost)\hat{\mathbf i}+(3sint)\hat{\mathbf j}+t^2\hat{\mathbf k}.\) The path is similar to that of a helix, although it is not a helix. The graph is shown here:

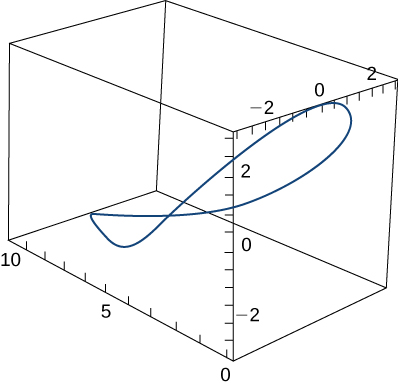
Find

a) the velocity and acceleration vectors

b) the glider’s speed at any time

c) the times, if any, at which the glider’s acceleration is orthogonal to its velocity

Answer

b) speed= \(\sqrt{9+4t^2}\)

Exercise \(\PageIndex{5}\)

Given that \(\vec{r(t)}=⟨e^{−5t} sin t,e^{−5t} cost,4e^{−5t}⟩ \) is the position vector of a moving particle, find the following quantities:

a) The velocity of the particle

b) The speed of the particle

c) The acceleration of the particle

Answer

a) \(\vec{v(t)}=⟨e^{−5t}(cost−5sint),−e^{−5t}(sint+5cost),−20e^{−5t}⟩\)

c) \(\vec{ a(t)}=⟨e^{−5t}(−sint−5cost)−5e^{−5t}(cost−5sint), −e^{−5t}(cost−5sint)+5e^{−5t} (sint+5cost),100e^{−5t}⟩\)

Exercise \(\PageIndex{6}\)

Find the maximum speed of a point on the circumference of an automobile tire of radius \(1\) ft when the automobile is travelling at \( 55 \) mph.

Exercise \(\PageIndex{7}\)

A projectile is shot in the air from ground level with an initial velocity of 500 m/sec at an angle of 60° with the horizontal. The graph is shown here:

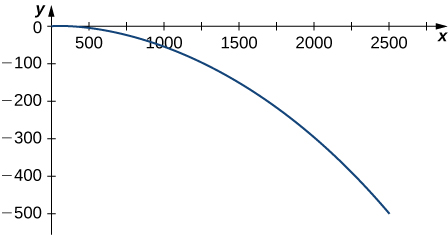
a) At what time does the projectile reach maximum height?

b) What is the approximate maximum height of the projectile?

c) At what time is the maximum range of the projectile attained?

d) What is the maximum range?

e) What is the total flight time of the projectile?

Answer

a) \(44.185\) sec, c) \(t=88.37\) sec, e) 88.37 sec

Exercise \(\PageIndex{8}\)

1) A projectile is fired at a height of 1.5 m above the ground with an initial velocity of 100 m/sec and at an angle of 30° above the horizontal. Use this information to answer the following questions:

a) Determine the maximum height of the projectile.

b) Determine the range of the projectile.

2) A golf ball is hit in a horizontal direction off the top edge of a building that is 100 ft tall. How fast must the ball be launched to land 450 ft away?

3) A projectile is fired from ground level at an angle of 8° with the horizontal. The projectile is to have a range of 50 m. Find the minimum velocity necessary to achieve this range.

4) Prove that an object moving in a straight line at constant speed has an acceleration of zero.

Answer

1b) The range is approximately 886.29 m.

3) 42.16 m/sec

Exercise \(\PageIndex{9}\)

1) The acceleration of an object is given by \(\vec{a(t)}=t\hat{\mathbf j}+t\hat{\mathbf k}.\) The velocity at \(t=1\) sec is \(\vec{ v(1)}=5\hat{\mathbf j}\), and the position of the object at \(t=1\) sec is \(\vec{r(1)}=0\hat{\mathbf i}+0\hat{\mathbf j}+0\hat{\mathbf k}\) Find the object’s position at any time.

2) Find \(\vec{r(t)}\) given that \(\vec{a(t)}=−32\hat{\mathbf j}, \vec{v(0)}=6003 \hat{\mathbf i} +600\hat{\mathbf j}, \) and \(\vec{ r(0)}=0.\)

Answer

1) \(\vec{r(t)}=0\hat{\mathbf i}+(\frac{1}{6}t^3+4.5t−\frac{14}{3})\hat{\mathbf j}+(\frac{1}{6}t^{3}−\frac{1}{2}t-\frac{1}{3})\hat{\mathbf k}\)

Exercise \(\PageIndex{10}\)

1) Find the tangential and normal components of acceleration for \(\vec{r(t)}=acos(ωt)\hat{\mathbf i}+bsin(ωt)\hat{\mathbf j} \) at \(t=0.\)

2) Given \(\vec{r(t)}=t^2\hat{\mathbf i}+2t\hat{\mathbf j}\) and find the tangential and normal components of acceleration at \(t=1.\)

Answer

1) \(0, aω^2\)

Exercise \(\PageIndex{11}\)

For each of the following problems, find the tangential and normal components of acceleration.

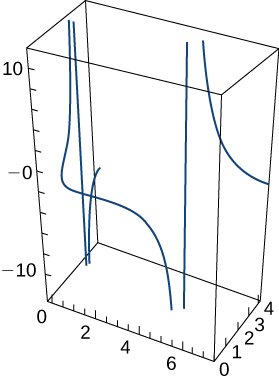
1) \(\vec{r(t)}=⟨e^tcost,e^tsint,e^t⟩.\) The graph is shown here:

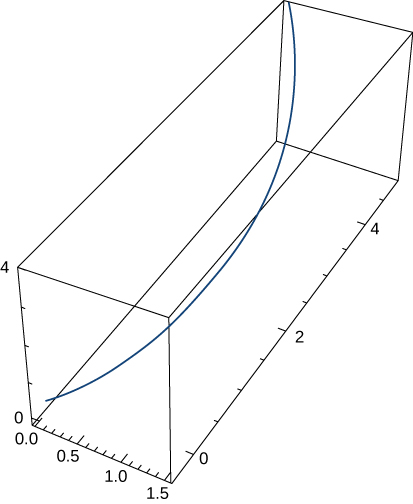
2) \(\vec{r(t)}=⟨cos(2t),sin(2t),1⟩\)

3) \(\vec{r(t)}= ⟨2t,t^2,t^3⟩\)

4) \(\vec{r(t)}= t^2\hat{\mathbf i}+t^2 \hat{\mathbf j}+t^3\hat{\mathbf k}\)

5) \(\vec{r(t)}= 3cos(2πt) \hat{\mathbf i}+3sin(2πt)\hat{\mathbf j}\)

Answer

1) \(3e^t, 2e^t\)

3) \(2t, 4+2t^2\)

5) \(0,23π\)

Exercise \(\PageIndex{12}\)

1) Find the position vector-valued function \(\vec{r(t)}\) given that \(\vec{a(t)}=\hat{\mathbf i}+e^t\hat{\mathbf j}, \vec{v(0)}=2\hat{\mathbf j}, and \vec{r(0)}=2i.\)

2) The force on a particle is given by \(\vec{f(t)}=(cost)\hat{\mathbf i}+(sint)\hat{\mathbf j}.\) The particle is located at point \((c,0)\) at \(t=0.\) The initial velocity of the particle is given by \(\vec{v(0)}=v_0j.\) Find the path of the particle of mass m. (Recall, \(F=m⋅a.\))

3) An automobile that weighs 2700 lb makes a turn on a flat road while travelling at 56 ft/sec. If the radius of the turn is 70 ft, what is the required frictional force to keep the car from skidding?

4) Using Kepler’s laws, it can be shown that \(v_0=2GMr\) is the minimum speed needed when \(θ=0\) so that an object will escape from the pull of a central force resulting from mass M. Use this result to find the minimum speed when \(θ=0\) for a space capsule to escape from the gravitational pull of Earth if the probe is at an altitude of 300 km above Earth’s surface.

5) Find the time in years it takes the dwarf planet Pluto to make one orbit about the Sun given that \(a=39.5 A.U.\)

6) Suppose that the position function for an object in three dimensions is given by the equation \(\vec{r(t)}=tcos(t) \hat{\mathbf i} +tsin(t) \hat{\mathbf j}+3t\hat{\mathbf k}.\)

a) Show that the particle moves on a circular cone.

b) Find the angle between the velocity and acceleration vectors when \(t=1.5.\)

c) Find the tangential and normal components of acceleration when \(t=1.5.\)

Answer

2)\(\vec{r(t)}=(−1mcost+c+1m)\hat{\mathbf i}+(−sintm+(v_0+1m)t)\hat{\mathbf j}\)

4)\(10.94 km/sec\)

6) \(0.43 m/sec^2, 2.46 m/sec^2\)