7.5E:

Exercise $\PageIndex{1}$

In the following exercises, evaluate the triple integrals $$\iiint_E f(x,y,z) dV$$ over the solid $E$.

1.

$f(x,y,z) = z, \quad B = \big\{(x,y,z)\, | \,x^2 + y^2 \leq 9, \quad x \leq 0, \quad y \leq 0, \quad 0 \leq z \leq 1\big\}$

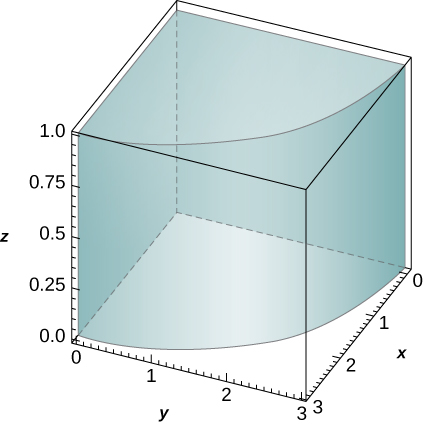
Answer

$\frac{9\pi}{8}$

2. $f(x,y,z) = xz^2, \space B = \{(x,y,z) | x^2 + y^2 \leq 16, \space x \geq 0, \space y \leq 0, \space -1 \leq z \leq 1\}$

3.

$f(x,y,z) = xy, \space B = \big\{(x,y,z)\, | \,x^2 + y^2 \leq 1, \space x \geq 0, \space x \geq y, \space -1 \leq z \leq 1\big\}$

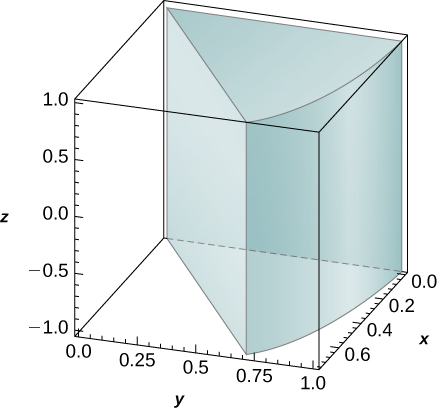
Answer

$\frac{1}{8}$

4. $f(x,y,z) = x^2 + y^2, \space B = \{(x,y,z) | x^2 + y^2 \leq 4, \space x \geq 0, \space x \leq y, \space 0 \leq z \leq 3\}$

5. $f(x,y,z) = e^{\sqrt{x^2+y^2}}, \space B = \{(x,y,z) | 1 \leq x^2 + y^2 \leq 4, \space y \leq 0, \space x \leq y\sqrt{3}, \space 2 \leq z \leq 3 \}$

Answer

$\frac{\pi e^2}{6}$

6. $f(x,y,z) = \sqrt{x^2 + y^2}, \space B = \{(x,y,z) | 1 \leq x^2 + y^2 \leq 9, \space y \leq 0, \space 0 \leq z \leq 1\}$

Exercise $\PageIndex{2}$

7.

a. Let $B$ be a cylindrical shell with inner radius $a$ outer radius $b$, and height $c$ where $0 < a < b$ and $c>0$. Assume that a function $F$ defined on $B$ can be expressed in cylindrical coordinates as $F(x,y,z) = f(r) + h(z)$, where $f$ and $h$ are differentiable functions. If $$\int_a^b \bar{f} (r) dr = 0$$ and $\bar{h}(0) = 0$, where $\bar{f}$ and $\bar{h}$ are antiderivatives of $f$ and $h$, respectively, show that

$$\iiint_B F(x,y,z) dV = 2\pi c (b\bar{f} (b) - a \bar{f}(a)) + \pi(b^2 - a^2) \bar{h} (c).$$

b. Use the previous result to show that

$$\iiint_B \left(z + sin \sqrt{x^2 + y^2}\right) dx \space dy \space dz = 6 \pi^2 ( \pi - 2),$$

where $B$ is a cylindrical shell with inner radius $\pi$ outer radius $2\pi$, and height $2$.

8.

a. Let $B$ be a cylindrical shell with inner radius $a$ outer radius $b$ and height $c$ where $0 < a < b$ and $c > 0$. Assume that a function $F$ defined on $B$ can be expressed in cylindrical coordinates as F(x,y,z) = f(r) g(\theta) f(z)\), where $f, \space g,$ and $h$ are differentiable functions. If $$\int_a^b \tilde{f} (r) dr = 0,$$ where $\tilde{f}$ is an antiderivative of $f$, show that

$$\iiint_B F (x,y,z)dV = [b\tilde{f}(b) - a\tilde{f}(a)] [\tilde{g}(2\pi) - \tilde{g}(0)] [\tilde{h}(c) - \tilde{h}(0)],$$

where $\tilde{g}$ and $\tilde{h}$ are antiderivatives of $g$ and $h$, respectively.

b. Use the previous result to show that $$\iiint_B z \space sin \sqrt{x^2 + y^2} dx \space dy \space dz = - 12 \pi^2,$$ where $B$ is a cylindrical shell with inner radius $\pi$ outer radius $2\pi$, and height $2$.

Exercise $\PageIndex{3}$

In the following exercises, the boundaries of the solid $E$ are given in cylindrical coordinates.

a. Express the region $E$ in cylindrical coordinates.

b. Convert the integral $$\iiint_E f(x,y,z) dV$$ to cylindrical coordinates.

9. E is bounded by the right circular cylinder $r = 4 \space sin \space \theta$, the $r\theta$-plane, and the sphere $r^2 + z^2 = 16$.

Answer

a. $E = \{(r,\theta,z) | 0 \leq \theta \leq \pi, \space 0 \leq r \leq 4 \space sin \space \theta, \space 0 \leq z \leq \sqrt{16 - r^2}\}$

b. $$\int_0^{\pi} \int_0^{4 \space sin \space \theta} \int_0^{\sqrt{16-r^2}} f(r,\theta, z) r \space dz \space dr \space d\theta$$

10. $E$ is bounded by the right circular cylinder $r = cos \space \theta$, the $r\theta$-plane, and the sphere $r^2 + z^2 = 9$.

11. $E$ is located in the first octant and is bounded by the circular paraboloid $z = 9 - 3r^2$, the cylinder $r = \sqrt{r}$, and the plane $r(cos \space \theta + sin \space \theta) = 20 - z$.

Answer

a. \(E = \{(r,\theta,z) |0 \leq \theta \leq \frac{\pi}{2}, \space 0 \leq r \leq \sqrt{3}, \space 9 - r^2 \leq z \leq 10 - r(cos \space \theta + sin \space \theta)\};

b. $$\int_0^{\pi/2} \int_0^{\sqrt{3}} \int_{9-r^2}^{10-r(cos \space \theta + sin \space \theta)} f(r,\theta,z) r \space dz \space dr \space d\theta$$

12. $E$ is located in the first octant outside the circular paraboloid $z = 10 - 2r^2$ and inside the cylinder $r = \sqrt{5}$ and is bounded also by the planes $z = 20$ and $\theta = \frac{\pi}{4}$.

Exercise $\PageIndex{4}$

The following exercises give the function $f$ and region $E$.

a. Express the region $E$ and the function $f$ in cylindrical coordinates.

b. Convert the integral $$\iiint_B f(x,y,z) dV$$ into cylindrical coordinates and evaluate it.

13. $f(x,y,z) = \frac{1}{x+3}$, $E = \{(x,y,z) | 0 \leq x^2 + y^2 \leq 9, \space x \geq 0, \space y \geq 0, \space 0 \leq z \leq x + 3\}$

Answer

a. $E = \{(r,\theta,z) | 0 \leq r \leq 3, \space 0 \leq \theta \leq \frac{\pi}{2}, \space 0 \leq z \leq r \space cos \space \theta + 3\},f(r,\theta,z) = \frac{1}{r \space cos \space \theta + 3};$

b. $$\int_0^3 \int_0^{\pi/2} \int_0^{r \space cos \space \theta+3} \frac{r}{r \space cos \space \theta + 3} dz \space d\theta \space dr = \frac{9\pi}{4}$$

14. $f(x,y,z) = x^2 + y^2, \space E = \{(x,y,z) |0 \leq x^2 + y^2 \leq 4, \space y \geq 0, \space 0 \leq z \leq 3 - x$

15. $f(x,y,z) = x, \space E = \{(x,y,z) | 1 \leq y^2 + z^2 \leq 9, \space 0 \leq x \leq 1 - y^2 - z^2\}$

Answer

a. $y = r \space cos \space \theta, \space z = r \space sin \space \theta, \space x = z,\space E = \{(r,\theta,z) | 1 \leq r \leq 3, \space 0 \leq \theta \leq 2\pi, \space 0 \leq z \leq 1 - r^2\}, \space f(r,\theta,z) = z$;

b. $$\int_1^3 \int_0^{2\pi} \int_0^{1-r^2} z r \space dz \space d\theta \space dr = \frac{256 \pi}{3}$$

16. $f(x,y,z) = y, \space E = \{(x,y,z) | 1 \leq x^2 + z^2 \leq 9, \space 0 \leq y \leq 1 - x^2 - z^2 \}$

Exercise $\PageIndex{5}$

In the following exercises, find the volume of the solid $E$ whose boundaries are given in rectangular coordinates.

17. $E$ is above the $xy$-plane, inside the cylinder $x^2 + y^2 = 1$, and below the plane $z = 1$.

Answer

$\pi$

18. $E$ is below the plane $z = 1$ and inside the paraboloid $z = x^2 + y^2$.

19. $E$ is bounded by the circular cone $z = \sqrt{x^2 + y^2}$ and $z = 1$.

Answer

$\frac{\pi}{3}$

20. $E$ is located above the $xy$-plane, below $z = 1$, outside the one-sheeted hyperboloid $x^2 + y^2 - z^2 = 1$, and inside the cylinder $x^2 + y^2 = 2$.

21. $E$ is located inside the cylinder $x^2 + y^2 = 1$ and between the circular paraboloids $z = 1 - x^2 - y^2$ and $z = x^2 + y^2$.

Answer

$\dfrac{\pi}{4}$

22. $E$ is located inside the sphere $x^2 + y^2 + z^2 = 1$, above the $xy$-plane, and inside the circular cone $z = \sqrt{x^2 + y^2}$.

23. $E$ is located outside the circular cone $x^2 + y^2 = (z - 1)^2$ and between the planes $z = 0$ and $z = 2$.

Answer

$\frac{2\pi}{3}$

24. $E$ is located outside the circular cone $z = 1 - \sqrt{x^2 + y^2}$, above the $xy$-plane, below the circular paraboloid, and between the planes $z = 0$ and $z = 2$.

Exercise $\PageIndex{6}$

25. [T] Use a computer algebra system (CAS) to graph the solid whose volume is given by the iterated integral in cylindrical coordinates $\displaystyle \int_{-\pi/2}^{\pi/2} \int_0^1 \int_{r^2}^r r \, dz \, dr \, d\theta.$ Find the volume $V$ of the solid. Round your answer to four decimal places.

Answer

$V = \frac{pi}{12} \approx 0.2618$

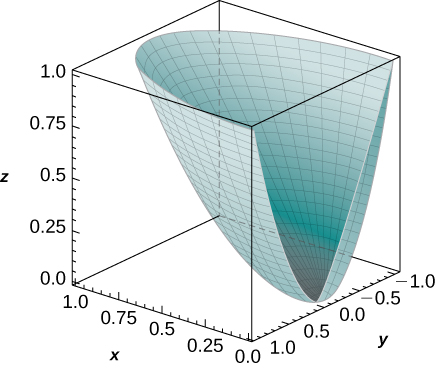
26. [T] Use a CAS to graph the solid whose volume is given by the iterated integral in cylindrical coordinates $\displaystyle \int_0^{\pi/2} \int_0^1 \int_{r^4}^r r \, dz \, dr \, d\theta.$ Find the volume $E$ of the solid. Round your answer to four decimal places.

Exercise $\PageIndex{7}$

27. Convert the integral $$\int_0^1 \int_{-\sqrt{1-z^2}}^{\sqrt{1-y^2}} \int_{x^2+y^2}^{\sqrt{x^2+y^2}} xz \space dz \space dx \space dy$$ into an integral in cylindrical coordinates.

Answer

\[\int_0^1 \int_0^{\pi} \int_{r^2}^r zr^2 \space cos \space \theta \space dz \space d\theta \space dr\

28. Convert the integral $$\int_0^2 \int_0^x \int_0^1 (xy + z) dz \space dx \space dy$$ into an integral in cylindrical coordinates.

Exercise $\PageIndex{8}$

In the following exercises, evaluate the triple integral $$\iiint_B f(x,y,z)dV$$ over the solid $B$.

29. $f(x,y,z) = 1, \space B = \{(x,y,z) | x^2 + y^2 + z^2 \leq 90, \space z \geq 0\}$

30. $f(x,y,z) = 1, \space B = \big\{(x,y,z)\, | \,x^2 + y^2 + z^2 \leq 90, \space z \geq 0\big\}$

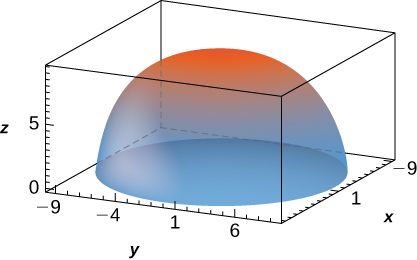
[Hide Solution]

Answer

$180 \pi \sqrt{10}$

31. $f(x,y,z) = 1 - \sqrt{x^2 + y^2 + z^2}, \space B = \big\{(x,y,z)\, | \,x^2 + y^2 + z^2 \leq 9, \space y \geq 0, \space z \geq 0\big\}$

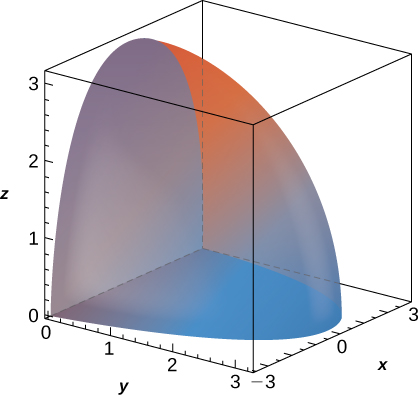
32. $f(x,y,z) = \sqrt{x^2 + y^2}, \space B$ is bounded above by the half-sphere $x^2 + y^2 + z^2 = 9$ with $z \geq 0$ and below by the cone $z^2 = x^2 + y^2$.

Answer

$\frac{81\pi(\pi - 2)}{16}$

33. $f(x,y,z) = \sqrt{x^2 + y^2}, \space B$ is bounded above by the half-sphere $x^2 + y^2 + z^2 = 16$ with $z \geq 0$ and below by the cone $2z^2 = x^2 + y^2$.

Exercise $\PageIndex{9}$

34. Show that if $F ( \rho,\theta,\varphi) = f(\rho)g(\theta)h(\varphi)$ is a continuous function on the spherical box $B = \big\{(\rho,\theta,\varphi)\, | \,a \leq \rho \leq b, \space \alpha \leq \theta \leq \beta, \space \gamma \leq \varphi \leq \psi\big\}$, then $\displaystyle\iiint_B F \space dV = \left(\int_a^b \rho^2 f(\rho) \space dr \right) \left( \int_{\alpha}^{\beta} g (\theta) \space d\theta \right)\left( \int_{\gamma}^{\psi} h (\varphi) \space \sin \varphi \space d\varphi \right).$

35. A function $F$ is said to have spherical symmetry if it depends on the distance to the origin only, that is, it can be expressed in spherical coordinates as $F(x,y,z) = f(\rho)$, where $\rho = \sqrt{x^2 + y^2 + z^2}$. Show that $\displaystyle\iiint_B F(x,y,z) \,dV = 2\pi \int_a^b \rho^2 f(\rho) \,d\rho,$ where $B$ is the region between the upper concentric hemispheres of radii $a$ and $b$ centered at the origin, with $0 < a < b$ and $F$ a spherical function defined on $B$.

Use the previous result to show that $\displaystyle\iiint_B (x^2 + y^2 + z^2) \sqrt{x^2 + y^2 + z^2} dV = 21 \pi,$ where $B = \big\{(x,y,z)\, | \,1 \leq x^2 + y^2 + z^2 \leq 2, \space z \geq 0\big\}$.

36. Let $B$ be the region between the upper concentric hemispheres of radii a and b centered at the origin and situated in the first octant, where $0 < a < b$. Consider F a function defined on B whose form in spherical coordinates $(\rho,\theta,\varphi)$ is $F(x,y,z) = f(\rho)\cos \varphi$. Show that if $g(a) = g(b) = 0$ and $\displaystyle\int_a^b h (\rho) \, d\rho = 0,$ then $\displaystyle\iiint_B F(x,y,z)\,dV = \frac{\pi^2}{4} [ah(a) - bh(b)],$ where $g$ is an antiderivative of $f$ and $h$ is an antiderivative of $g$.

Use the previous result to show that $\displaystyle \iiint_B = \frac{z \cos \sqrt{x^2 + y^2 + z^2}}{\sqrt{x^2 + y^2 + z^2}} \, dV = \frac{3\pi^2}{2},$ where $B$ is the region between the upper concentric hemispheres of radii $\pi$ and $2\pi$ centered at the origin and situated in the first octant.

Exercise $\PageIndex{10}$

The following exercises give the function $f$ and region $E$.

a. Express the region $E$ and function $f$ in spherical coordinates.

b. Convert the integral $$\iiint_B f(x,y,z)dV$$ into cylindrical coordinates and evaluate it.

37. $f(x,y,z) = z; \space E = \{(x,y,z) | 0 \leq x^2 + y^2 + z^2 \leq 1, \space z \geq 0\}$

38. $f(x,y,z) = x + y; \space E = \{(x,y,z) | 1 \leq x^2 + y^2 + z^2 \leq 2, \space z \geq 0, \space y \geq 0\}$

Answer

a. $f(\rho,\theta, \varphi) = \rho \space sin \space \varphi \space (cos \space \theta + sin \space \theta), \space E = \{(\rho,\theta,\varphi) | 1 \leq \rho \leq 2, \space 0 \leq \theta \leq \pi, \space 0 \leq \varphi \leq \frac{\pi}{2}\}$;

b. $$\int_0^{\pi} \int_0^{\pi/2} \int_1^2 \rho^3  \space sin^2 \space \varphi  (cos \space \theta + sin \space \theta) \space d\rho \space d\varphi \space d\theta = \frac{15\pi}{8}$$

39. $f(x,y,z) = 2xy; \space E = \{(x,y,z) | \sqrt{x^2 + y^2} \leq z \leq \sqrt{1 - x^2 - y^2}, \space x \geq 0, \space y \geq 0\}$

40. $f(x,y,z) = z; \space E = \{(x,y,z) | x^2 + y^2 + z^2 - 2z\leq 0, \space \sqrt{x^2 + y^2} \leq z\}$

Answer

a. $f(\rho,\theta,\varphi) = \rho \space cos \space \varphi; \space E = \{(\rho,\theta,\varphi) | 0 \leq \rho \leq 2 \space cos \space \varphi, \space 0 \leq \theta \leq 2 \pi, \space 0 \leq \varphi \leq \frac{\pi}{4}\}$;

b. $$\int_0^{2\pi} \int_0^{\pi/4} \int_0^{2 \space cos \space \varphi} \rho^3 sin \space \varphi \space cos \space \varphi \space d\rho \space d\varphi \space d\theta = \frac{7\pi}{6}$$

Exercise $\PageIndex{11}$

In the following exercises, find the volume of the solid $E$ whose boundaries are given in rectangular coordinates.

41. $E = \{ (x,y,z) | \sqrt{x^2 + y^2} \leq z \leq \sqrt{16 - x^2 - y^2}, \space x \geq 0, \space y \geq 0\}$

42. $E = \{ (x,y,z) | x^2 + y^2 + z^2 - 2z \leq 0, \space \sqrt{x^2 + y^2} \leq z\}$

Answer

\(\pi\

 

)

43. Use spherical coordinates to find the volume of the solid situated outside the sphere $\rho = 1$ and inside the sphere $\rho = cos \space \varphi$, with $\varphi \in [0,\frac{\pi}{2}]$.

44. Use spherical coordinates to find the volume of the ball $\rho \leq 3$ that is situated between the cones $\varphi = \frac{\pi}{4}$ and $\varphi = \frac{\pi}{3}$.

Answer

$9\pi (\sqrt{2} - 1)$

45. Convert the integral$\int_{-4}^4 \int_{-\sqrt{16-y^2}}^{\sqrt{16-y^2}} \int_{-\sqrt{16-x^2-y^2}}^{\sqrt{16-x^2-y^2}} (x^2 + y^2 + z^2) \, dz \, dx \, dy$ into an integral in spherical coordinates.

46. Convert the integral $\displaystyle \int_0^4 \int_0^{\sqrt{16-x^2}} \int_{-\sqrt{16-x^2-y^2}}^{\sqrt{16-x^2-y^2}} (x^2 + y^2 + z^2)^2 \, dz \space dy \space dx$ into an integral in spherical coordinates.

Answer

$\displaystyle\int_0^{\pi/2} \int_0^{\pi/2} \int_0^4 \rho^6 \sin \varphi \, d\rho \, d\phi \, d\theta$

47. Convert the integral

$\displaystyle \int_{-2}^2 \int_{-\sqrt{4-x^2}}^{\sqrt{4-x^2}} \int_{\sqrt{x^2+y^2}}^{\sqrt{16-x^2-y^2}} \, dz \space dy \space dx$

into an integral in spherical coordinates and evaluate it.

 

Exercise $\PageIndex{14}$

48. [T] Use a CAS to graph the solid whose volume is given by the iterated integral in spherical coordinates

$\displaystyle \int_{\pi/2}^{\pi} \int_{5\pi}^{\pi/6} \int_0^2 \rho^2 \sin \varphi \space d\rho \space d\varphi \space d\theta.$

Find the volume $V$ of the solid. Round your answer to three decimal places.

Answer

$V = \frac{4\pi\sqrt{3}}{3} \approx 7.255$

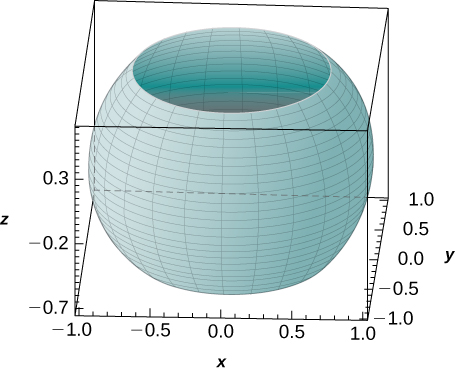
49. [T] Use a CAS to graph the solid whose volume is given by the iterated integral in spherical coordinates as

$\displaystyle \int_0^{2\pi} \int_{3\pi/4}^{\pi/4} \int_0^1 \rho^2 \sin \varphi \space d\rho \space d\varphi \space d\theta.$

Find the volume $V$ of the solid. Round your answer to three decimal places.

50. [T] Use a CAS to evaluate the integral $\displaystyle \iiint_E (x^2 + y^2) \, dV$ where $E$ lies above the paraboloid

$z = x^2 + y^2$ and below the plane $z = 3y$.

Answer

$\frac{343\pi}{32}$

51. [T]

a. Evaluate the integral $$\iiint_E e^{\sqrt{x^2+y^2+z^2}}dV,$$ where $E$ is bounded by spheres $4x^2 + 4y^2 + 4z^2 = 1$ and

$x^2 + y^2 + z^2 = 1$.

b. Use a CAS to find an approximation of the previous integral. Round your answer to two decimal places.

Exercise $\PageIndex{14}$

52. Express the volume of the solid inside the sphere $x^2 + y^2 + z^2 = 16$ and outside the cylinder $x^2 + y^2 = 4$as triple integrals

in cylindrical coordinates and spherical coordinates, respectively.

Answer

$\displaystyle \int_0^{2\pi}\int_2^4\int_{−\sqrt{16−r^2}}^{\sqrt{16−r^2}}r\,dz\,dr\,dθ$ and

$\displaystyle \int_{\pi/6}^{5\pi/6}\int_0^{2\pi}\int_{2\csc \phi}^{4}\rho^2\sin \rho \, d\rho \, d\theta \, d\phi$

 

53. Express the volume of the solid inside the sphere $x^2 + y^2 + z^2 = 16$ and outside the cylinder $x^2 + y^2 = 4$ that is located in the first octant as triple integrals in cylindrical coordinates and spherical coordinates, respectively.

 

Exercise $\PageIndex{15}$

54. The power emitted by an antenna has a power density per unit volume given in spherical coordinates by

$p(\rho,\theta,\varphi) = \frac{P_0}{\rho^2} cos^2 \theta \space sin^4 \varphi$, where $P_0$ is a constant with units in watts. The total power within a sphere $B$ of radius $r$ meters is defined as $$P = \iiint_B p(\rho,\theta,\varphi) \space dV.$$ Find the total power $P$.

Answer

$P = \frac{32P_0 \pi}{3}$ watts

55. Use the preceding exercise to find the total power within a sphere $B$ of radius 5 meters when the power density per unit volume is given by

$p(\rho, \theta,\varphi) = \frac{30}{\rho^2} cos^2 \theta \space sin^4 \varphi$.

56. A charge cloud contained in a sphere $B$ of radius r centimeters centered at the origin has its charge density given by

$q(x,y,z) = k\sqrt{x^2 + y^2 + z^2}\frac{\mu C}{cm^3}$, where $k > 0$.

The total charge contained in $B$ is given by $$Q = \iiint_B q(x,y,z) dV.$$ Find the total charge $Q$.

Answer

$Q = kr^4 \pi \mu C$

57. Use the preceding exercise to find the total charge cloud contained in the unit sphere if the charge density is

$q(x,y,z) = 20 \sqrt{x^2 + y^2 + z^2} \frac{\mu C}{cm^3}$.

 

 

 

 

Contributors

Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.