9.4E: EXERCISES

Last updated
Save as PDF

Page ID: 26275

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Exercise $\PageIndex{1}$

For the following exercises, evaluate the line integrals by applying Green’s theorem.

1. $\int_C 2xydx+(x+y)dy$, where $C $ is the path from $(0, 0)$ to $(1, 1)$ along the graph of $y=x^3$ and from $(1, 1)$ to $(0, 0)$ along the graph of $y=x$ oriented in the counterclockwise direction.

2. $\int_C2xydx+(x+y)dy$, where $C $ is the boundary of the region lying between the graphs of $y=0$ and $y=4−x^2$ oriented in the counterclockwise direction.

Answer: $\int_C 2xydx+(x+y)dy=\frac{32}{3}$

3. $\int_C 2 arctan(\frac{y}{x})dx+ln(x^2+y^2)dy$, where $C $ is defined by $x=4+2cosθ,y=4sinθ$ oriented in the counterclockwise direction

4. $\int_C sinx cosydx+(xy+cosx siny)dy$, where $C $ is the boundary of the region lying between the graphs of $y=x$ and $y=\sqrt{x}$ oriented in the counterclockwise direction

Answer: $\int_C sinxcosydx+(xy+cosxsiny)dy=\frac{1}{12}$

5. $\int_C xydx+(x+y)dy$, where $C $ is the boundary of the region lying between the graphs of $x^2+y^2=1$ and $x^2+y^2=9$ oriented in the counterclockwise direction

6. $∮_C(−ydx+xdy)$, where $C $ consists of line segment $C_1 $ from $(−1,0)$ to $(1, 0)$, followed by the semicircular arc $C_2 $ from $(1, 0)$ back to $(1, 0)$

Answer: $∮_C (−ydx+xdy)=π$

Exercise $\PageIndex{2}$

For the following exercises, use Green’s theorem.

7. Let $C $ be the curve consisting of line segments from $(0, 0)$ to $(1, 1)$ to $(0, 1)$ and back to $(0, 0)$. Find the value of $\int_Cxydx+\sqrt{y^2+1}dy$.

8. Evaluate line integral $\int_Cxe^{−2x}dx+(x^4+2x^2y^2)dy$, where $C $ is the boundary of the region between circles $x^2+y^2=1$ and $x^2+y^2=4$, and is a positively oriented curve.

Answer: $\int_Cxe^{−2x}dx+(x^4+2x^2y^2)dy=0$

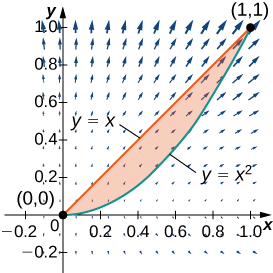
9. Find the counterclockwise circulation of field $F(x,y)=xy \, \hat{ \mathbf i} +y^2 \, \hat{ \mathbf j} $ around and over the boundary of the region enclosed by curves $y=x^2$ and $y=x$ in the first quadrant and oriented in the counterclockwise direction.

$A vector field with focus on quadrant 1. A line is drawn from (0,0) to (1,1) according to function y=x, and a curve is also drawn according to the function y=x^2. The region enclosed between the two functions is shaded. Te=he arrows closer to the origin are much smaller than those further away, particularly vertically. The arrows point up and away from the origin to the right in the part of quadrant 1 shown.$

10. Evaluate $∮_Cy^3dx−x^3y^2dy$, where $C $ is the positively oriented circle of radius 2 centered at the origin.

Answer: $∮_Cy^3dx−x^3dy=−24π$

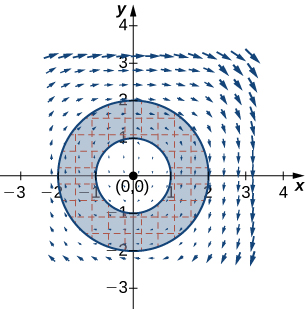
11. Evaluate $∮_Cy^3dx−x^3dy$, where $C $ includes the two circles of radius 2 and radius 1 centered at the origin, both with positive orientation.

$A vector field in two dimensions. The arrows surround the origin in a clockwise circular motion. Those close to the origin are much smaller than those further away. A circle of radius 2 and a circle of radius with centers at the origin is drawn in, and the region between the two is shaded.$

12. Calculate $∮_C−x^2ydx+xy^2dy$, where $C $ is a circle of radius 2 centered at the origin and oriented in the counterclockwise direction.

Answer: $∮_C−x^2ydx+xy^2dy=8π$

13. Calculate integral $∮_C 2[y+xsin(y)]dx+[x^2cos(y)−3y^2]dy$ along triangle $C $ with vertices $(0, 0), (1, 0)$ and $(1, 1)$, oriented counterclockwise, using Green’s theorem.

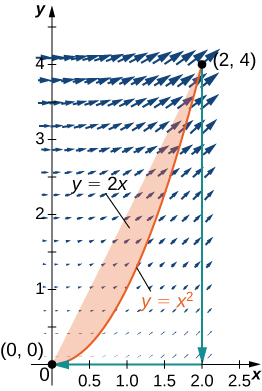
14. Evaluate integral $∮_C(x^2+y^2)dx+2xydy$, where $C $ is the curve that follows parabola $y=x^2$ from $(0,0),(2,4),$ then the line from $(2, 4)$ to $(2, 0)$, and finally the line from $(2, 0)$ to $(0, 0)$.

$A vector field in quadrant 1. The arrows are much smaller closer to the origin. They point up and away from the origin, with increasing slope the further they are to the right. The curve follows the parabola y=x^2 from the origin to (2,4), the line from (2,4) to (2,0), and the line from (2,0) to (0,0). The area under y=2x and above the parabola is shaded.$

Answer: $∮_C(x^2+y^2)dx+2xydy=0$

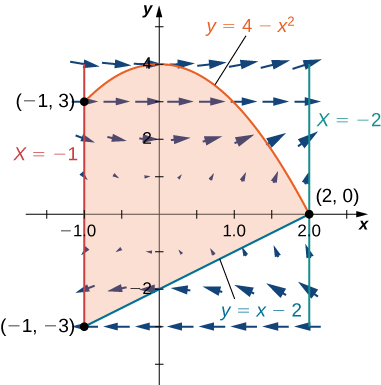
15. Evaluate line integral $∮_C(y−sin(y)cos(y))dx+2xsin^2(y)dy$, where $C $ is oriented in a counterclockwise path around the region bounded by $x=−1,x=2,y=4−x^2$, and $y=x−2$.

$A vector field in two dimensions. The arrows are smaller the closer they are to the origin, particular vertically. Curve C follows a counterclockwise path around the region bounded by x=-1, x=2, y = 4-x^2, and y = x-2. The region is shaded.$

Answer: TBA

Exercise $\PageIndex{3}$

For the following exercises, use Green’s theorem to find the area.

16. Find the area between ellipse $\frac{x^2}{9}+\frac{y^2}{4}=1$ and circle $x^2+y^2=25$.

Answer: $A=19π$

17. Find the area of the region enclosed by parametric equation

$ p(\theta) = ( \cos(\theta) - \cos^2(\theta)) \, \hat{ \mathbf i} - (\sin(\theta)- \cos(\theta) \sin(\theta)) \, \hat{ \mathbf j}$ for $0≤θ≤2π.$

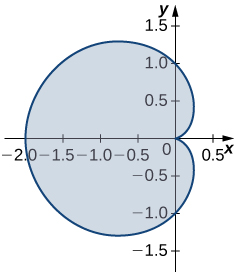
$A cardioid beginning at the origin, going through (0,1), (-2,0), (0,-1), and back to the origin.$

18. Find the area of the region bounded by hypocycloid $ \vecs{r}(t)=\cos^3(t) \, \hat{ \mathbf i} + \sin^3(t) \, \hat{ \mathbf j}$. The curve is parameterized by $t∈[0,2π].$

Answer: $A=\frac{3}{8π}$

19. Find the area of a pentagon with vertices $(0,4),(4,1),(3,0),(−1,−1),$ and $(−2,2)$.

Answer: TBA

Exercise $\PageIndex{4}$

20. Use Green’s theorem to evaluate $\int_{C+}(y^2+x^3)dx+x^4dy$, where $C^+$ is the perimeter of square $[0,1]×[0,1]$ oriented counterclockwise.

Answer: $\int_C+(y^2+x^3)dx+x^4dy=0$

21. Use Green’s theorem to prove the area of a disk with radius a is $A=πa^2$.

22. Use Green’s theorem to find the area of one loop of a four-leaf rose $r=3sin2θ$. (Hint: $xdy−ydx=r^2dθ$).

Answer: $A=\frac{9π}{8}$

23. Use Green’s theorem to find the area under one arch of the cycloid given by parametric plane $x=t−sint,y=1−cost,t≥0.$

24. Use Green’s theorem to find the area of the region enclosed by curve $\vecs{r}(t)=t^2 \, \hat{ \mathbf i} + \left(\dfrac{t^3}{3}-t \right) \, \hat{ \mathbf j}, -\sqrt{3} \leq t \leq \sqrt{3}.$

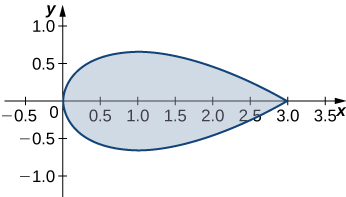
$A horizontal teardrop-shaped region symmetric about the x axis and a-intercepts at the origin and (3,0). The larger, curved end is at the origin, and the pointed end is at (3,0).$

Answer: $A=\frac{8\sqrt{3}}{5}$

25. [T] Evaluate Green’s theorem using a computer algebra system to evaluate the integral $\int_Cxe^ydx+e^xdy$, where $C $ is the circle given by $x^2+y^2=4$ and is oriented in the counterclockwise direction.

26. Evaluate $\int_C(x^2y−2xy+y^2)ds$, where $C $ is the boundary of the unit square $0≤x≤1,0≤y≤1$, traversed counterclockwise.

Answer: $\int_C(x^2y−2xy+y^2)ds=3$

27. Evaluate $\int_C\dfrac{−(y+2)dx+(x−1)dy}{(x−1)^2+(y+2)^2}$, where $C $ is any simple closed curve with an interior that does not contain point $(1,−2)$ traversed counterclockwise.

28. Evaluate $\int_C\dfrac{xdx+ydy}{x^2+y^2}$, where $C $ is any piecewise, smooth simple closed curve enclosing the origin, traversed counterclockwise.

Answer: $\int_C\dfrac{xdx+ydy}{x^2+y^2}=2π$

Exercise $\PageIndex{5}$

For the following exercises, use Green’s theorem to calculate the work done by force $\vecs{F}$ on a particle that is moving counterclockwise around closed path $C $.

29. $\vecs{F}(x,y)=xy \, \hat{ \mathbf i} +(x+y) \, \hat{ \mathbf j}, C:x^2+y^2=4$

30. $ \vecs{F}(x,y)= \left( x^{\frac{3}{2}}-3y \right) \, \hat{ \mathbf i} +(6x+5 \sqrt{y}) \, \hat{ \mathbf j}$, $ C$ : boundary of a triangle with vertices $(0, 0), (5, 0),$ and $(0, 5)$

Answer: $W=\frac{225}{2}$

Exercise $\PageIndex{6}$

31. Evaluate $\int_C(2x^3−y^3)dx+(x^3+y^3)dy$, where $C $ is a unit circle oriented in the counterclockwise direction.

32. A particle starts at point $(−2,0)$, moves along the x-axis to $(2, 0)$, and then travels along semicircle $y=\sqrt{4−x^2}$ to the starting point. Use Green’s theorem to find the work done on this particle by force field $ \vecs{F}(x,y)= x \, \hat{ \mathbf i} + ( x^3+ 3 x y^2) \, \hat{ \mathbf j}$.

Answer: $W=12π$

33. David and Sandra are skating on a frictionless pond in the wind. David skates on the inside, going along a circle of radius 2 in a counterclockwise direction. Sandra skates once around a circle of radius 3, also in the counterclockwise direction. Suppose the force of the wind at point $(x,y) (x,y) (x,y)$ is $\vecs{F}(x,y)=(x^2y+10y) \, \hat{ \mathbf i}+(x^3+2xy^2) \, \hat{ \mathbf j}$. Use Green’s theorem to determine who does more work.

34. Use Green’s theorem to find the work done by force field $\vecs{F}(x,y)=(3y−4x) \, \hat{ \mathbf i}+(4x−y) \, \hat{ \mathbf j}$ when an object moves once counterclockwise around ellipse $4x^2+y^2=4.$

Answer: $W=12π$

35. Use Green’s theorem to evaluate line integral $∮_Ce^{2x}sin2ydx+e^{2x}cos2ydy$, where $C $ is ellipse $9(x−1)^2+4(y−3)^2=36$ oriented counterclockwise.

36. Evaluate line integral $∮_Cy^2dx+x^2dy$, where $C $ is the boundary of a triangle with vertices $(0,0),(1,1)$, and $(1,0)$, with the counterclockwise orientation.

Answer: $∮_Cy^2dx+x^2dy=\frac{1}{3}$

37. Use Green’s theorem to evaluate line integral $\int_C\vecs{H}·\vecs{dr} $ if $\vecs{H}(x,y)=e^y \, \hat{ \mathbf i}−sin(πx) \, \hat{ \mathbf j}$, where $C $ is a triangle with vertices $(1, 0), (0, 1),$ and $(−1,0),(−1,0)$ traversed counterclockwise.

38. Use Green’s theorem to evaluate line integral $\int_C\sqrt{1+x^3}dx+2xydy$ where $C $ is a triangle with vertices $(0, 0), (1, 0),$ and $(1, 3)$ oriented clockwise.

Answer: $\int_C\sqrt{1+x^3}dx+2xydy=3$

39. Use Green’s theorem to evaluate line integral $\int_Cx^2ydx−xy^2dy$ where $C $ is a circle $x^2+y^2=4$ oriented counterclockwise.

40. Use Green’s theorem to evaluate line integral $\int_C(3y−e^{sinx})dx+(7x+\sqrt{y^4+1})dy$ where $C $ is circle $x^2+y^2=9$ oriented in the counterclockwise direction.

Answer: $\int_C(3y−e^{sinx})dx+(7x+\sqrt{y^4+1})dy=36π$

41. Use Green’s theorem to evaluate line integral $\int_C(3x−5y)dx+(x−6y)dy$, where $C $ is ellipse $\frac{x^2}{4}+y^2=1$ and is oriented in the counterclockwise direction.

$A horizontal oval oriented counterclockwise with vertices at (-2,0), (0,-1), (2,0), and (0,1). The region enclosed is shaded.$

Answer: TBA

Exercise $\PageIndex{7}$: Use Green's theorem

42. Let $C $ be a triangular closed curve from (0, 0) to (1, 0) to (1, 1) and finally back to (0, 0). Let $ \vecs{F}(x,y)=4y \, \hat{ \mathbf i}+6x^2 \, \hat{ \mathbf j}.$ Use Green’s theorem to evaluate $∮_C\vecs{F}· \vecs{ds}.$

Answer: $∮_CF·dr=2$

43. Use Green’s theorem to evaluate line integral $ ∮_Cydx−xdy, $ where $C$ is circle $x^2+y^2=a^2$ oriented in the clockwise direction.

44. Use Green’s theorem to evaluate line integral $∮_C(y+x)dx+(x+siny)dy,$ where $C$ is any smooth simple closed curve joining the origin to itself oriented in the counterclockwise direction.

Answer: $ ∮_C(y+x)dx+(x+siny)dy=0$

45. Use Green’s theorem to evaluate line integral $∮C(y−ln(x^2+y^2))dx+(2arctan(y)x)dy,$ where $C$ is the positively oriented circle $(x−2)^2+(y−3)^2=1.$

46. Use Green’s theorem to evaluate $ ∮_Cxydx+x^3y^3dy,$ where $C$ is a triangle with vertices $(0, 0), (1, 0),$ and $(1, 2)$ with positive orientation.

Answer: $∮_Cxydx+x^3y^3dy=2221$

47. Use Green’s theorem to evaluate line integral $∫_Csinydx+x cosydy,$ where $C$ is ellipse $x^2+xy+y^2=1$ oriented in the counterclockwise direction.

48. Let $\vecs{F}(x,y)=(\cos(x^5))−13y^3)\, \hat{ \mathbf i} +13x^3\, \hat{ \mathbf j}$. Find the counterclockwise circulation $∮_C \vecs{F}· \vecs{dr}$, where $C$ is a curve consisting of the line segment joining $(−2,0)$ and $(−1,0),$ half circle $ y= \sqrt{1−x^2}$, the line segment joining $(1, 0) $ and $(2, 0),$ and half circle $y= \sqrt{4−x^2}$

Answer: $∮_C \vecs{F}· \vecs{dr}=15π^4$

49. Use Green’s theorem to evaluate line integral $∫_Csin(x^3)dx+2ye^{x^2}dy,$ where $C$ is a triangular closed curve that connects the points $(0, 0), (2, 2),$ and $(0, 2)$ counterclockwise.

50. Let $C$ be the boundary of square $0≤x≤π,0≤y≤π,$ traversed counterclockwise. Use Green’s theorem to find $∫_Csin(x+y)dx+cos(x+y)dy.$

Answer: $∫_Csin(x+y)dx+cos(x+y)dy=4$

51. Use Green’s theorem to evaluate line integral $\int_C\vecs{F}·\vecs{dr} $, where $ \vecs{F}(x,y)=(y^2−x^2) \, \hat{ \mathbf i}+(x^2+y^2)\, \hat{ \mathbf j}, $ and $C$ is a triangle bounded by $y=0,x=3,$ and $y=x,$ oriented counterclockwise.

52. Use Green’s Theorem to evaluate integral $\int_C\vecs{F}·\vecs{dr} $, where$ \vecs{F}(x,y)=(xy^2)\, \hat{ \mathbf i}+x\, \hat{ \mathbf j}$, and $C$ is a unit circle oriented in the counterclockwise direction.

Answer: $\int_C\vecs{F}·\vecs{dr} =π$

53. Use Green’s theorem in a plane to evaluate line integral $∮_C(xy+y^2)dx+x^2dy,$ where $ C$ is a closed curve of a region bounded by $y=x$ and $y=x^2 $ oriented in the counterclockwise direction.

54. Calculate the outward flux of $ \vecs{F}=−x \, \hat{ \mathbf i}+2y \, \hat{ \mathbf j}$ over a square with corners $ (±1,±1) $, where the unit normal is outward pointing and oriented in the counterclockwise direction.

Answer: $∮_C \vecs{F}·\vecs{n} ds=4$

55. [T] Let $ C$ be circle $ x^2+y^2=4 $ oriented in the counterclockwise direction. Evaluate $∮_C(3y−e^{tan^{−1}(x))}dx+(7x+y^4+1)dy$ using a computer algebra system.

56. Find the flux of field $ \vecs{F}=-x \, \hat{ \mathbf i} +y \, \hat{ \mathbf j} $ across $ x^2+y^2=16 $ oriented in the counterclockwise direction.

Answer: $∮_C \vecs{F}·\vecs{n} ds=32π$

57. Let $ \vecs{F}=(y^2−x^2)\, \hat{ \mathbf i}+(x^2+y^2) \, \hat{ \mathbf j},$ and let $C$ be a triangle bounded by $ y=0,x=3,$ and $ y=x$ oriented in the counterclockwise direction. Find the outward flux of $\vecs{F}$ through $C$.

58. [T] Let $C$ be unit circle $x^2+y^2=1$ traversed once counterclockwise. Evaluate $∫_C[−y^3+sin(xy)+xy cos(xy)]dx+[x^3+x^2cos(xy)]dy $ by using a computer algebra system.

Answer: $∫_C[−y^3+sin(xy)+xy cos(xy)]dx+[x^3+x^2cos(xy)]dy= 4.7124 $

59. [T] Find the outward flux of vector field $ \vecs{F}=xy^2\, \hat{ \mathbf i}+x^2y\, \hat{ \mathbf j}$ across the boundary of annulus $R={(x,y):1≤x^2+y^2≤4}={(r,θ):1≤r≤2,0≤θ≤2π} $ using a computer algebra system.

60. Consider region R bounded by parabolas $ y=x^2$ and $x=y^2. $ Let be the boundary of R oriented counterclockwise. Use Green’s theorem to evaluate

$ ∮_C(y+e^{\sqrt{x}})dx+(2x+ \cos(y^2))dy$

Answer: $ ∮_C(y+e^{\sqrt{x}})dx+(2x+ \cos(y^2))dy=13$