1. Introduction to Sets, Venn Diagrams, and Partitions

Last updated
Save as PDF

Page ID: 19840

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Contents:

Sets, elements, set-builder notation (at 2:53 in this video, I should have said "less than 7" instead of "less than or equal to 7").
Subsets
Unions, intersections, and the empty set
Complements
Cartesian Products
Introduction to Venn diagrams and shading sets
Determining which set are shaded in a Venn diagram
Definition and examples of partitions
The number of elements in a set: notation, examples, and cartesian products
The number of elements in a set: partitions and an example

Example $\PageIndex{1}$

Write a set which contains all the members of your household (and nothing else). Then, write this same set in set-builder notation.

Solution

Let's call this set $H$. For me, $H=\{Kylee, Ranjan\}$. In set-builder notation, one way to do this would be $H=\{y: y \text{ lives in Ranjan's house}\}$.

Example $\PageIndex{2}$

Let $M$ be the set of all the students in this class and let $S$ be the set of all Saint Mary's students. Is $S\subset M$? Is $M\subset S$? Is $S=M$?

Solution

$M\subset S$ is the only one that is true, since all students in this class are Saint Mary's students.

Example $\PageIndex{3}$

Let $C$ be the set of professors who teach computer science classes and let $M$ be the set of professors who teach math classes. Describe $M\cup C$ and $M\cap C$ in words.

Solution

$M\cup C$ is the set of professors who teach math or computer science or both and $M\cap C$ is the set of professors who teach both math and computer science.

Example $\PageIndex{4}$

Let $U$ be the set of people on campus and let $B=\{x: x \text{ is a person on campus who brushed their teeth this morning}\}$. Describe the set $B^c$ in words and write it in set-builder notation.

Solution

$B^c$ is the set of people on campus who did not brush their teeth this morning, which we can write in set-builder notation as follows: $B^c=\{z: z \text{ is a person on campus who did not brush their teeth this morning}\}$.

Example $\PageIndex{5}$

We can think about a deck of cards as a cartesian product of two sets. Let $S=\{hearts, diamonds, spades, clubs\}$ and $R=\{ace, king, queen, jack, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1\}$. Then each card in the deck represents an element of the set $S\times R$.

Example $\PageIndex{6}$

Suppose $S$ is the set of all students in this room. There are many ways to partition $S$. I could partition the students by the row in which they are sitting. I could partition the class by putting the students into groups.

Example $\PageIndex{7}$

Suppose that $n(A)=20$ and that $A$ is partitioned into two sets, $B$ and $C$. Furthermore, suppose that the number of elements in $B$ is three times the number of elements in $C$. How many elements are in $B$ and how many are in $C$?

Solution

Since $B$ and $C$ form a partition of $A$, and we know that $A$ has 20 elements, we know \[n(B)+n(C)=20.\] We can then translate "the number of elements in $B$ is three times the number of elements in $C$" into an equation as \[n(B)=3n(C).\] We plug this equation into the first one to get that $3n(C)+n(C)=20$ which simplifies to $4n(C)=20$. Dividing both sides by 4, we get that $n(C)=5$. Plugging this back into either equation, we get $n(B)=15$.

PREWORK 1 - Wednesday:

Let $A=\{e,n,o,u,g,h\}$ and $B=\{s,n,o,w\}$. Determine $A\cap B$ and $A\cup B$.
Let $U$ be the set of all Saint Mary's students. Let $A$ be the set of Saint Mary's students who live on campus and let $B$ be the set of Saint Mary's Students who are athletes. Describe the set $A^c$ in words. Then describe the set $A\cap B$ in words.

Prework 1 - Wednesday: tell Ranjan what you need help on!

PREWORK 1 - Friday:

Draw a Venn diagram with three sets $A$, $B$, and $C$ and shade in the area representing $A\cap B^c\cap C$.
Let $X=\{1,2,3,4,5,6,7,8,9,10\}$. Let $A=\{2,3,8\}$, $B=\{1,3,7,9\}$, and $C=\{3,4,6,10\}$. Does $\{A,B,C\}$ form a partition of $X$? Explain.

Prework 2 - Friday: tell Ranjan what you need help on!

Solutions to Wednesday Prework:

$A\cap B=\{n,o\}$ since only n and o appear in both sets. $A\cup B=\{e,n,o,u,g,h,s,w\}$ since we take all elements in either set, but get rid of repeats.
$A^c$ is the set of Saint Mary's students who live off campus, since $A^c$ contains all elements of $U$ not in $A$. $A\cap B$ is the set of Saint Mary's students who live on campus and are student athletes, since the intersection includes elements that are in both $A$ and $B$.

Solutions to Friday Prework:

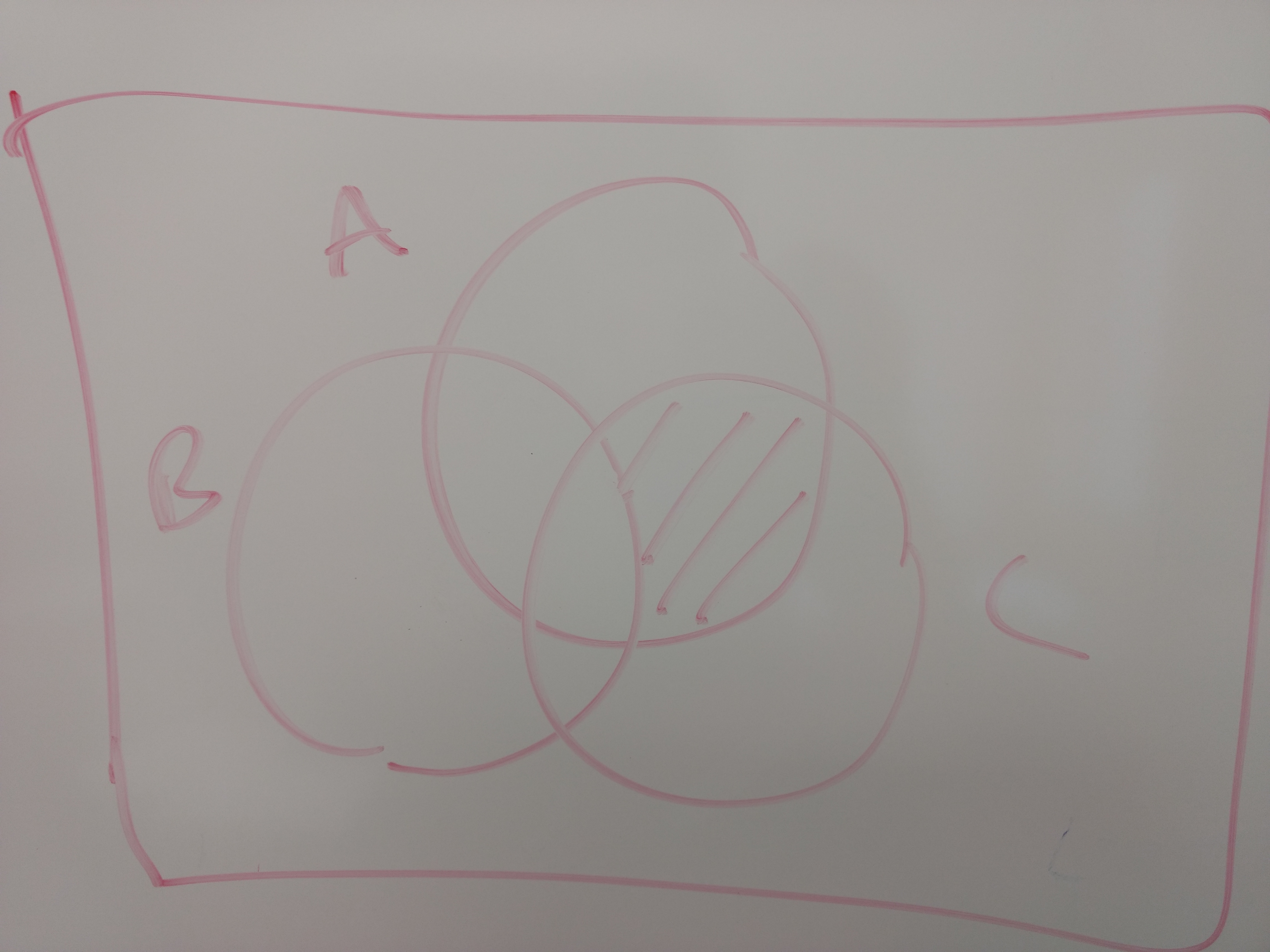$Prework1#3.jpg$ We need to shade all parts of the Venn diagram that are in $A$ and not in $B$ and in $C$.
No. To form a partition of $X$ we would need $A\cup B\cup C=X$ but none of them contain 5. Also we need no element to appear in more than one of $A$, $B$, and $C$, but 3 appears more than once.