10. Linear Programming Problems

Last updated
Save as PDF

Page ID: 26457

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Contents 10A:

Formulating a linear programming problem, example 1 (https://youtu.be/mGxjw1eTqss)
Formulating a linear programming problem, example 2 (https://youtu.be/aJCGI2APYoU)

Prework 10A:

Formulate (but do no solve) the following linear programming problem. A florist makes 2 special bouquets. Both types consist of Japanese irises and tulips. Type I consists of 1 dozen tulips and 1 dozen Japanese irises. Type II consists of 2 dozen tulips and 4 dozen Japanese irises. The profit on each Type I bouquet is $8 and the profit on each Type II bouquet is $18. The florist knows that they sell at least 8 Type I bouquets each day, so they always make at least 8 of these each day. There are only 60 dozen tulips and 100 dozen irises available each day. How many of each type of bouquet should the shop make each day to maximize profit?

Prework 10A Google form

Solutions

Let $x$ be the number of Type I bouquets and $y$ be the number of Type II bouquets. Find $x$ and $y$ in order to maximize the daily profit $P = 8x+18y$ subject to $x \ge 8 $, $x+2y \le 60$, $x+4y \le 100$, and $y \ge 0$.

Contents 10B:

Finding the feasible set and corner points for a system of linear inequalities, example 1 (https://youtu.be/roESHLZYgGY)
Finding the feasible set and corner points for a system of linear inequalities, example 2 (https://youtu.be/SrZlXx1LvAM)

Prework 10B:

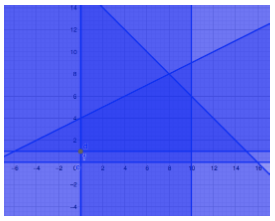
Graph the feasible region to the following system of linear inequalities: $x+y\leq 16$, $2y-x\leq 8$, $x\leq 10$, $y\geq 1$, $x,y\geq 0$.

Prework 10B Google form

Solutions

The corner points are (0,1), (0,4), (8,8), (10,6), (10,1). The feasible region is the darkest area in the picture below (the up-pointing pentagon in the middle). $feasibleregion.png$

Contents 10C:

Solving the linear programming problem in video 1 in 10A. (https://youtu.be/BAsQsisz_I0)
Solving the linear programming problem in video 2 in 10A. (https://youtu.be/CRliN48IGNU)

Prework 10C:

A florist makes 2 special bouquets. Both types consist of Japanese irises and tulips. Type I consists of 1 dozen tulips and 1 dozen Japanese irises. Type II consists of 2 dozen tulips and 4 dozen Japanese irises. The profit on each Type I bouquet is $8 and the profit on each Type II bouquet is $18. The florist knows that they sell at least 8 Type I bouquets each day, so they always make at least 8 of these each day. There are only 60 dozen tulips and 100 dozen irises available each day. How many of each type of bouquet should the shop make each day to maximize profit?

Prework 10C Google form

Solution

We set up this problem in 10A. Let $x$ be the number of Type I bouquets and $y$ be the number of Type II bouquets. Find $x$ and $y$ in order to maximize the daily profit $P = 8x+18y$ subject to $x \ge 8 $, $x+2y \le 60$, $x+4y \le 100$, and $y \ge 0$. We now find the feasible region and the corner points. These are shown in the figure. We then plug in the corner points into the profit function. We find that the maximum profit is $520 when we make and sell 20 Type I and 20 Type II bouquets. $Screenshot 2024-12-04 at 10.07.24 AM.png$

Search

Text Color

Text Size

Margin Size

Font Type