14. Solving Linear Programming Problems
- Page ID
- 26458
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
The following topics are included in this series of two videos.
- Solving the linear programming problem in video 1 in Chapter 13.
- Solving the linear programming problem in video 2 in Chapter 13.
Prework
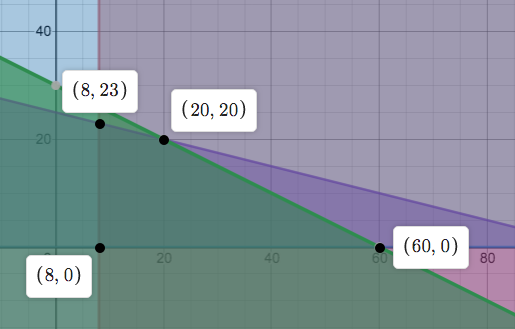
- A florist makes 2 special bouquets. Both types consist of Japanese irises and tulips. Type I consists of 1 dozen tulips and 1 dozen Japanese irises. Type II consists of 2 dozen tulips and 4 dozen Japanese irises. The profit on each Type I bouquet is $8 and the profit on each Type II bouquet is $18. The florist knows that they sell at least 8 Type I bouquets each day, so they always make at least 8 of these each day. There are only 60 dozen tulips and 100 dozen irises available each day. How many of each type of bouquet should the shop make each day to maximize profit?
Solution
- We set up this problem in section 13. Let \(x\) be the number of Type I bouquets and \(y\) be the number of Type II bouquets. Find \(x\) and \(y\) in order to maximize the daily profit \(P = 8x+18y\) subject to \(x \ge 8 \), \(x+2y \le 60\), \(x+4y \le 100\), and \(x,y \ge 0\). We now find the feasible region and the corner points. These are shown in the figure below. We then plug in the corner points into the profit function. We find that the maximum profit is $520 when we make and sell 20 Type I and 20 Type II bouquets.
