2. Sizes of Sets
- Page ID
- 20853
The following topics are included in this series of five videos.
- Determining the size of a set in a two set Venn diagram, first example
- Some useful formulas
- Second example
- Word problem example
- Three set Venn diagram problem
Method for solving these types of problems:
- If you have a word problem, first translate from English to math.
- Draw a Venn diagram, and start filling it in, from the inside.
- If you can fill in the entire diagram in this way, do so.
- If you cannot, put a variable where you get stuck and fill in the rest of the diagram in terms of that variable. Then solve for the variable.
- Answer the question.
PREWORK:
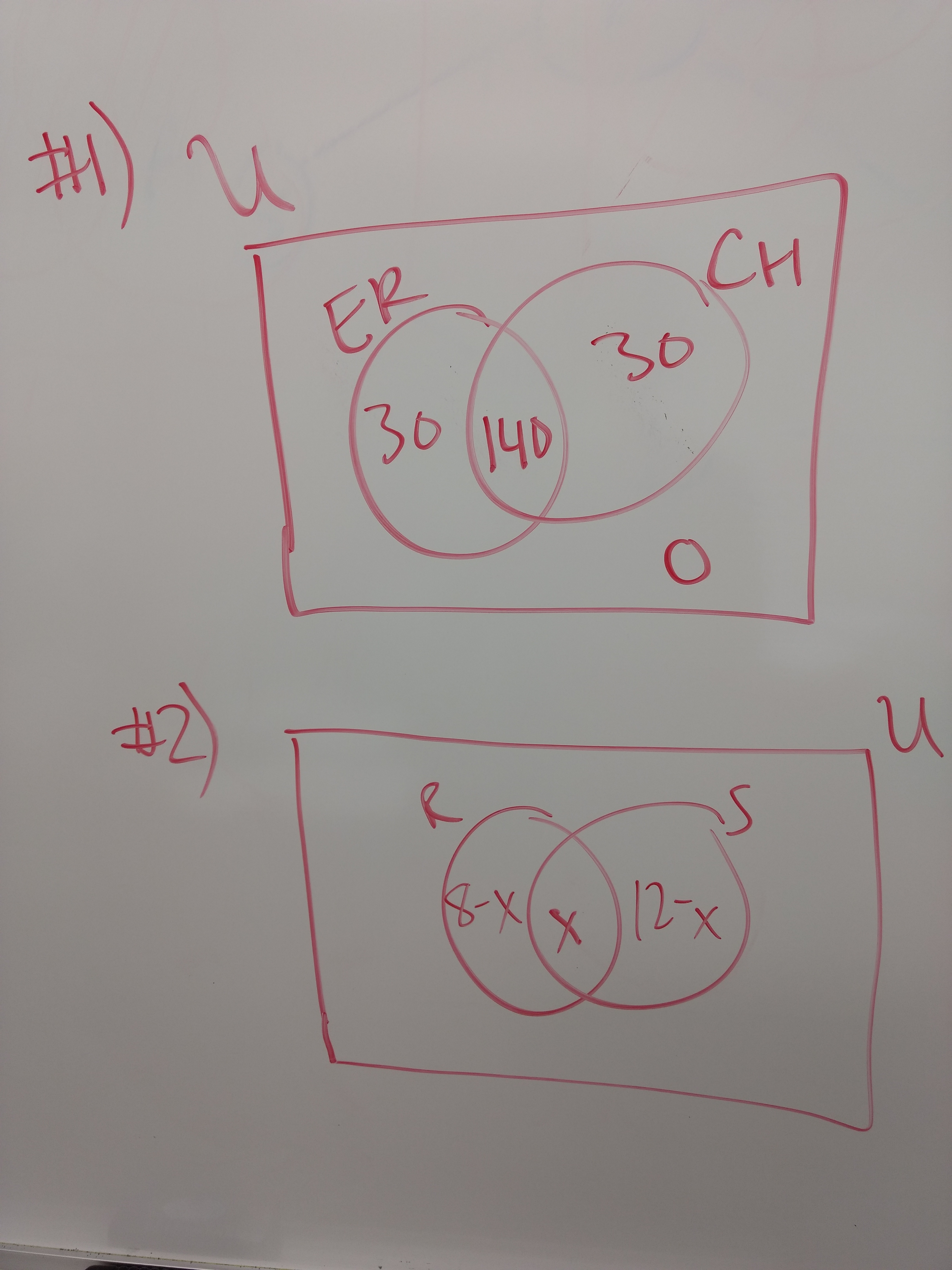
- A survey of 200 people was taken. We find 170 people like ER, 30 like Chicago Hope but not ER, and 140 like both Chicago Hope and ER. How many like neither show?
- If \(n(U) = 24, n(R) = 8, n(S) = 12\), and \(n(R \cup S) = 18\), what is \(n(R \cap S)\)?
Solutions:
1. We are using the upper Venn diagram. Since 140 people like both, we put that information in the intersection of the two sets. Thirty people like Chicago Hope but not ER, so we put 30 in the part of the set corresponding to Chicago Hope that does not overlap with the set corresponding to ER. Since 170 in total like ER, 170-140=30 like only ER. Finally, we notice that 30+140+30=200 people like at least one of the shows, so nobody likes neither.
2. We look at the bottom Venn diagram. Since we don't know \(n(R\cap S)\) we put a variable, \(x\) in the intersection. Since there are 8 elements in \(R\) total, there must be \(8-x\) elements only in \(R\). Likewise, there are \(12-x\) elements only in \(S\). Now \(8-x+x+12-x=18\) since \(n(R\cup S)=18\). We solve to get that \(x=2\). Therefore \(n(R\cap S)=2\).