2.0: Library of functions
( \newcommand{\kernel}{\mathrm{null}\,}\)
Thinking out Loud
What is the meaning of a real-valued function?
In this section, we provide a formal definition of a function and examine several ways in which functions are represented—namely, through tables, formulas, and graphs. We study formal notation and terms related to functions. We also define composition of functions and symmetry properties. Most of this material will be a review for you, but it serves as a handy reference to remind you of some of the algebraic techniques useful for working with functions.
Functions
Given two sets A and B a set with elements that are ordered pairs (x,y) where x is an element of A and y is an element of B, is a relation from A to B. A relation from A to B defines a relationship between those two sets. A function is a special type of relation in which each element of the first set is related to exactly one element of the second set. The element of the first set is called the input; the element of the second set is called the output. Functions are used all the time in mathematics to describe relationships between two sets. For any function, when we know the input, the output is determined, so we say that the output is a function of the input. For example, the area of a square is determined by its side length, so we say that the area (the output) is a function of its side length (the input). The velocity of a ball thrown in the air can be described as a function of the amount of time the ball is in the air. The cost of mailing a package is a function of the weight of the package. Since functions have so many uses, it is important to have precise definitions and terminology to study them.

Definition: Functions
A function f consists of a set of inputs, a set of outputs, and a rule for assigning each input to exactly one output. The set of inputs is called the domain of the function. The set of outputs is called the range of the function.
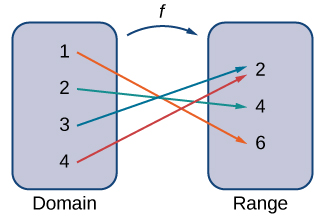
For example, consider the function f, where the domain is the set of all real numbers and the rule is to square the input. Then, the input x=3 is assigned to the output 32=9.
Since every nonnegative real number has a real-value square root, every nonnegative number is an element of the range of this function. Since there is no real number with a square that is negative, the negative real numbers are not elements of the range. We conclude that the range is the set of nonnegative real numbers.
For a general function f with domain D, we often use x to denote the input and y to denote the output associated with x. When doing so, we refer to x as the independent variable and \(y as the dependent variable, because it depends on x. Using function notation, we write y=f(x), and we read this equation as “y equals f of x.” For the squaring function described earlier, we write f(x)=x2.
The concept of a function can be visualized using Figures 2.0.1 - 2.0.3.
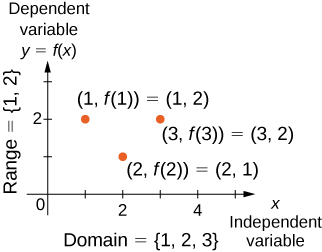
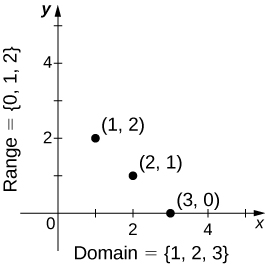
We can also visualize a function by plotting points (x,y) in the coordinate plane where y=f(x). The graph of a function is the set of all these points. For example, consider the function f, where the domain is the set D=1,2,3 and the rule is f(x)=3−x. In Figure 2.0.4, we plot a graph of this function.
Every function has a domain. However, sometimes a function is described by an equation, as in f(x)=x2, with no specific domain given. In this case, the domain is taken to be the set of all real numbers x for which f(x) is a real number. For example, since any real number can be squared, if no other domain is specified, we consider the domain of f(x)=x2 to be the set of all real numbers. On the other hand, the square root function f(x)=√x only gives a real output if x is nonnegative. Therefore, the domain of the function f(x)=√x is the set of nonnegative real numbers, sometimes called the natural domain.
For the functions f(x)=x2 and f(x)=√x, the domains are sets with an infinite number of elements. Clearly we cannot list all these elements. When describing a set with an infinite number of elements, it is often helpful to use set-builder or interval notation. When using set-builder notation to describe a subset of all real numbers, denoted R, we write
{x|x has some property}.
We read this as the set of real numbers x such that x has some property. For example, if we were interested in the set of real numbers that are greater than one but less than five, we could denote this set using set-builder notation by writing
{x|1<x<5}.
A set such as this, which contains all numbers greater than a and less than b, can also be denoted using the interval notation (a,b). Therefore,
(1,5)={x|1<x<5}.
The numbers 1 and 5 are called the endpoints of this set. If we want to consider the set that includes the endpoints, we would denote this set by writing
[1,5]={x|1<x<5}.
We can use similar notation if we want to include one of the endpoints, but not the other. To denote the set of nonnegative real numbers, we would use the set-builder notation
{x|0≤x}.
The smallest number in this set is zero, but this set does not have a largest number. Using interval notation, we would use the symbol ∞, which refers to positive infinity, and we would write the set as
[0,∞)={x|0≤x}.
It is important to note that ∞ is not a real number. It is used symbolically here to indicate that this set includes all real numbers greater than or equal to zero. Similarly, if we wanted to describe the set of all nonpositive numbers, we could write
(−∞,0]={x|x≤0}.
Here, the notation −∞ refers to negative infinity, and it indicates that we are including all numbers less than or equal to zero, no matter how small. The set
(−∞,∞)={x|x is any real number}
refers to the set of all real numbers.Some functions are defined using different equations for different parts of their domain. These types of functions are known as piecewise-defined functions. For example, suppose we want to define a function f with a domain that is the set of all real numbers such that f(x)=3x+1 for x≥ and f(x)=x2 forx<2.We denote this function by writing
f(x)={3x+1x≥2x2x<2
When evaluating this function for an input x,the equation to use depends on whether x≥2 or x<2. For example, since 5>2, we use the fact that f(x)=3x+1 for x≥2 and see that f(5)=3(5)+1=16. On the other hand, for x=−1, we use the fact that f(x)=x2 for x<2 and see that f(−1)=1.
Example 2.0.1: Evaluating Functions
For the function f(x)=3x2+2x−1, evaluate:
- f(−2)
- f(√2)
- f(a+h)
Solution
Substitute the given value for x in the formula for f(x).
- f(−2)=3(−2)2+2(−2)−1=12−4−1=7
- f(√2)=3(√2)2+2√x−1=6+2√2−1=5+2√2
- f(a+h)=3(a+h)2+2(a+h)−1=3(a2+2ah+h2)+2a+2h−1=3a2+6ah+3h2+2a+2h−1
Exercise 2.0.1
For f(x)=x2−3x+5, evaluate f(1) and f(a+h).
- Hint
-
Substitute 1 and a+h for x in the formula for f(x).
- Answer
-
f(1)=3 and f(a+h)=a2+2ah+h2−3a−3h+5
Example 2.0.2: Finding Domain and Range
For each of the following functions, determine the i. domain and ii. range.
- f(x)=(x−4)2+5
- f(x)=√3x+2−1
- f(x)=3x−2
Solution
1. Consider f(x)=(x−4)2+5.
1.Since f(x)=(x−4)2+5 is a real number for any real number x, the domain of f is the interval (−∞,∞).
2. Since (x−4)2≥0, we know f(x)=(x−4)2+5≥5. Therefore, the range must be a subset of {y|y≥5}. To show that every element in this set is in the range, we need to show that for a given y in that set, there is a real number x such that f(x)=(x−4)2+5=y. Solving this equation for x, we see that we need x such that
(x−4)2=y−5.
This equation is satisfied as long as there exists a real number x such that
x−4=±√y−5
Since y≥5, the square root is well-defined. We conclude that for x=4±√y−5,f(x)=y, and therefore the range is {y|y≥5 }.
2. Consider f(x)=√3x+2−1.
1.To find the domain of f,we need the expression 3x+2≥0. Solving this inequality, we conclude that the domain is {x|x≥−2/3 }.
2.To find the range of f,we note that since √3x+2≥0,f(x)=√3x+2−1≥−1. Therefore, the range of f must be a subset of the set {y|y≥−1}. To show that every element in this set is in the range of f, we need to show that for all y in this set, there exists a real number x in the domain such that f(x)=y. Let y≥−1. Then, f(x)=y if and only if
√3x+2−1=y.
Solving this equation for x, we see that x must solve the equation
√3x+2=y+1.
Since y≥−1, such an x could exist. Squaring both sides of this equation, we have 3x+2=(y+1)2.
Therefore, we need
3x=(y+1)2−2,
which implies
x=13(y+1)2−23.
We just need to verify that x is in the domain of f. Since the domain of fconsists of all real numbers greater than or equal to \frac{−2}{3}\), and
13(y+1)2−23≥−23,
there does exist an x in the domain of f. We conclude that the range of f is {y|y≥−1}.
3.Consider f(x)=3/(x−2).
1.Since 3/(x−2) is defined when the denominator is nonzero, the domain is {x|x≠2}.
2.To find the range of f, we need to find the values of y such that there exists a real number x in the domain with the property that
3x−2=y.
Solving this equation for x, we find that
x=3y+2.
Therefore, as long as y≠0, there exists a real number x in the domain such that f(x)=y. Thus, the range is {y|y≠0}.
Exercise 2.0.2
Find the domain and range for f(x)=√4−2x+5.
- Hint
-
Use 4−2x≥0.
- Answer
-
Domain = {x∣x≤2} and range = {y∣y≥5}
Representing Functions
Typically, a function is represented using one or more of the following tools:
- A table
- A graph
- A formula
We can identify a function in each form, but we can also use them together. For instance, we can plot on a graph the values from a table or create a table from a formula.
Tables
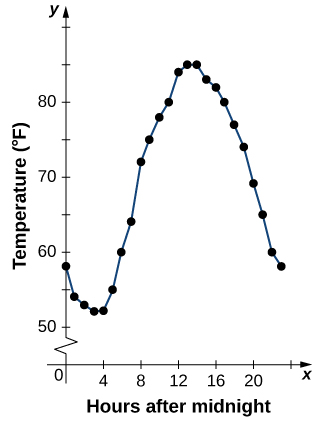
Functions described using a table of values arise frequently in real-world applications. Consider the following simple example. We can describe temperature on a given day as a function of time of day. Suppose we record the temperature every hour for a 24-hour period starting at midnight. We let our input variable x be the time after midnight, measured in hours, and the output variable y be the temperature x hours after midnight, measured in degrees Fahrenheit. We record our data in Table 2.0.1.
| Hour After Midnight | Temperature(°F) | Hour After Midnight | Temperature(°F) |
|---|---|---|---|
| 0 | 58 | 12 | 84 |
| 1 | 54 | 13 | 85 |
| 2 | 53 | 14 | 85 |
| 3 | 52 | 15 | 83 |
| 4 | 52 | 16 | 82 |
| 5 | 55 | 17 | 80 |
| 6 | 60 | 18 | 77 |
| 7 | 64 | 19 | 74 |
| 8 | 72 | 20 | 69 |
| 9 | 75 | 21 | 65 |
| 10 | 78 | 22 | 60 |
| 11 | 80 | 23 | 58 |
We can see from the table that temperature is a function of time, and the temperature decreases, then increases, and then decreases again. However, we cannot get a clear picture of the behavior of the function without graphing it.
Graphs
Given a function f described by a table, we can provide a visual picture of the function in the form of a graph. Graphing the temperatures listed in Table 2.0.1 can give us a better idea of their fluctuation throughout the day. Figure shows the plot of the temperature function.
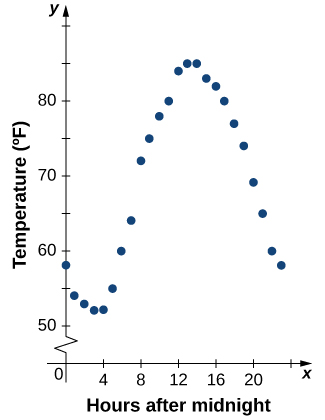
From the points plotted on the graph in Figure 2.0.5, we can visualize the general shape of the graph. It is often useful to connect the dots in the graph, which represent the data from the table. In this example, although we cannot make any definitive conclusion regarding what the temperature was at any time for which the temperature was not recorded, given the number of data points collected and the pattern in these points, it is reasonable to suspect that the temperatures at other times followed a similar pattern, as we can see in Figure 2.0.6.
Algebraic Formulas
Sometimes we are not given the values of a function in table form, rather we are given the values in an explicit formula. Formulas arise in many applications. For example, the area of a circle of radius r is given by the formula A(r)=πr^2. When an object is thrown upward from the ground with an initial velocity v_{0} ft/s, its height above the ground from the time it is thrown until it hits the ground is given by the formula s(t)=−16t^2+v_{0}t. When P dollars are invested in an account at an annual interest rate r compounded continuously, the amount of money after t years is given by the formula A(t)=Pe^{rt}. Algebraic formulas are important tools to calculate function values. Often we also represent these functions visually in graph form.
Given an algebraic formula for a function f, the graph of f is the set of points (x,f(x)), where x is in the domain of f and f(x) is in the range. To graph a function given by a formula, it is helpful to begin by using the formula to create a table of inputs and outputs. If the domain of f consists of an infinite number of values, we cannot list all of them, but because listing some of the inputs and outputs can be very useful, it is often a good way to begin.
When creating a table of inputs and outputs, we typically check to determine whether zero is an output. Those values of x where f(x)=0 are called the zeros of a function. For example, the zeros of f(x)=x^2−4 are x=±2. The zeros determine where the graph of f intersects the x-axis, which gives us more information about the shape of the graph of the function. The graph of a function may never intersect the x-axis, or it may intersect multiple (or even infinitely many) times.
Another point of interest is the y -intercept, if it exists. The y-intercept is given by (0,f(0)).
Since a function has exactly one output for each input, the graph of a function can have, at most, one y-intercept. If x=0 is in the domain of a function f, then f has exactly one y-intercept. If x=0 is not in the domain of f, then f has no y-intercept. Similarly, for any real number c, if c is in the domain of f, there is exactly one output f(c), and the line x=c intersects the graph of f exactly once. On the other hand, if c is not in the domain of f,f(c) is not defined and the line x=c does not intersect the graph of f. This property is summarized in the vertical line test.
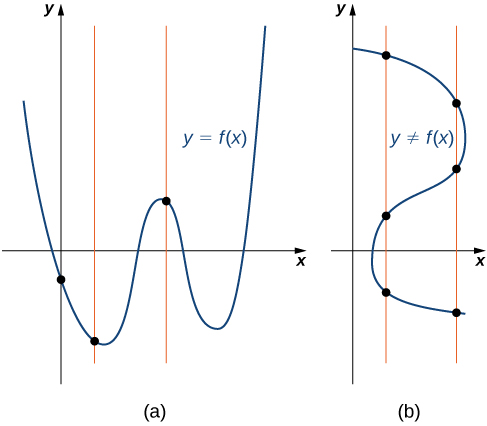
Vertical Line Test
Given a function f, every vertical line that may be drawn intersects the graph of f no more than once. If any vertical line intersects a set of points more than once, the set of points does not represent a function.
We can use this test to determine whether a set of plotted points represents the graph of a function (Figure \PageIndex{7}).
Example \PageIndex{3}: Finding Zeros and y-Intercepts of a Function
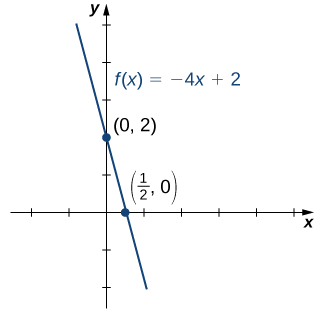
Consider the function f(x)=−4x+2.
- Find all zeros of f.
- Find the y-intercept (if any).
- Sketch a graph of f.
Solution
1.To find the zeros, solve f(x)=−4x+2=0. We discover that f has one zero at x=1/2.
2. The y-intercept is given by (0,f(0))=(0,2).
3. Given that f is a linear function of the form f(x)=mx+b that passes through the points (1/2,0) and (0,2), we can sketch the graph of f (Figure \PageIndex{8}).
Example \PageIndex{4}: Using Zeros and y-Intercepts to Sketch a Graph
Consider the function f(x)=\sqrt{x+3}+1.
- Find all zeros of f.
- Find the y-intercept (if any).
- Sketch a graph of f.
Solution
1.To find the zeros, solve \sqrt{x+3}+1=0. This equation implies \sqrt{x+3}=−1. Since \sqrt{x+3}≥0 for all x, this equation has no solutions, and therefore f has no zeros.
2.The y-intercept is given by (0,f(0))=(0,\sqrt{3}+1).
3.To graph this function, we make a table of values. Since we need x+3≥0, we need to choose values of x≥−3. We choose values that make the square-root function easy to evaluate.
| x | -3 | -2 | 1 |
|---|---|---|---|
| f(x) | 1 | 2 | 3 |
Making use of the table and knowing that, since the function is a square root, the graph of f should be similar to the graph of y=\sqrt{x}, we sketch the graph (Figure \PageIndex{9}).
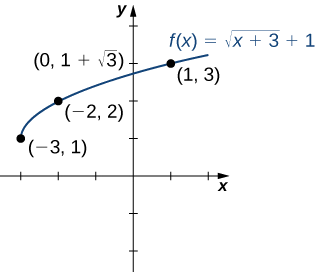
Exercise \PageIndex{4}
Find the zeros of f(x)=x^3−5x^2+6x.
- Hint
-
Factor the polynomial.
- Answer
-
x=0,2,3
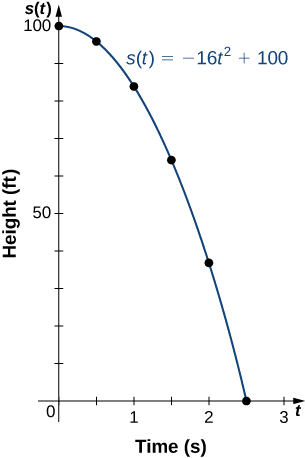
Example \PageIndex{5}: Finding the Height of a Free-Falling Object
If a ball is dropped from a height of 100 ft, its height s at time t is given by the function s(t)=−16t^2+100, where s is measured in feet and t is measured in seconds. The domain is restricted to the interval [0,c], where t=0 is the time when the ball is dropped and t=c is the time when the ball hits the ground.
- Create a table showing the height s(t) when t=0,0.5,1,1.5,2,and 2.5. Using the data from the table, determine the domain for this function. That is, find the time c when the ball hits the ground.
- Sketch a graph of s.
Solution
| t | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 |
|---|---|---|---|---|---|---|
| s(t) | 100 | 96 | 84 | 64 | 36 | 0 |
Since the ball hits the ground when t=2.5, the domain of this function is the interval [0,2.5].
2.
Definition: Increasing and Decreasing on an Interval
We say that a function f is increasing on the interval I if for all x_{1},x_{2}∈I,
f(x_{1})≤f(x_{2}) when x_{1}<x_{2}.
We say f is strictly increasing on the interval I if for all x_{1},x_{2}∈I,
f(x_{1})<f(x_{2}) when x_{1}<x_{2}.
We say that a function f is decreasing on the interval I if for all x_{1},x_{2}∈I,
f(x_{1})≥f(x_{2}) if x_{1}<x_{2}.
We say that a function f is strictly decreasing on the interval I if for all x_{1},x_{2}∈I,
f(x_{1})>f(x_{2}) if x_{1}<x_{2}.
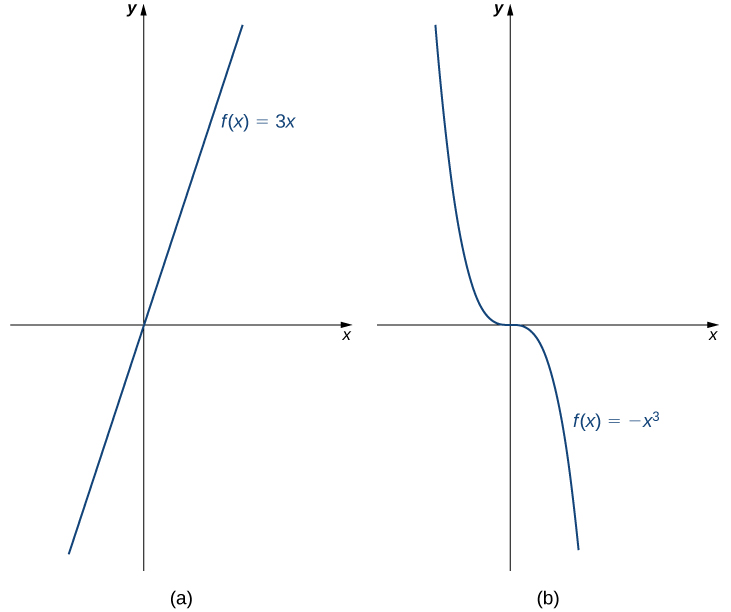
For example, the function f(x)=3x is increasing on the interval (−∞,∞) because 3x_{1}<3x_{2} whenever x_{1}<x_{2}. On the other hand, the function f(x)=−x^3 is decreasing on the interval (−∞,∞) because −x^3_{1}>−x^3_{2} whenever x_{1}<x_{2} (Figure \PageIndex{10}).
Combining Functions
Now that we have reviewed the basic characteristics of functions, we can see what happens to these properties when we combine functions in different ways, using basic mathematical operations to create new functions. For example, if the cost for a company to manufacture x items is described by the function C(x) and the revenue created by the sale of x items is described by the function R(x), then the profit on the manufacture and sale of x items is defined as P(x)=R(x)−C(x). Using the difference between two functions, we created a new function.
Alternatively, we can create a new function by composing two functions. For example, given the functions f(x)=x^2 and g(x)=3x+1, the composite function f∘g is defined such that
(f∘g)(x)=f(g(x))=(g(x))^2=(3x+1)^2.
The composite function g∘f is defined such that
(g∘f)(x)=g(f(x))=3f(x)+1=3x^2+1.
Note that these two new functions are different from each other.
Combining Functions with Mathematical Operators
To combine functions using mathematical operators, we simply write the functions with the operator and simplify. Given two functions f and g, we can define four new functions:
| (f+g)(x)=f(x)+g(x) | Sum |
| (f−g)(x)=f(x)−g(x) | Difference |
| (f·g)(x)=f(x)g(x) | Product |
| (\frac{f}{g})(x)=\frac{f(x)}{g(x)} forg(x)≠0 | Quotient |
Example \PageIndex{6}: Combining Functions Using Mathematical Operations
Given the functions f(x)=2x−3 and g(x)=x^2−1, find each of the following functions and state its domain.
- (f+g)(x)
- (f−g)(x)
- (f·g)(x)
- (\frac{f}{g})(x)
Solution
1. (f+g)(x)=(2x−3)+(x^2−1)=x^2+2x−4.
The domain of this function is the interval (−∞,∞).
2.(f−g)(x)=(2x−3)−(x^2−1)=−x^2+2x−2.
The domain of this function is the interval (−∞,∞).
3. (f·g)(x)=(2x−3)(x^2−1)=2x^3−3x^2−2x+3.
The domain of this function is the interval (−∞,∞).
4. (\frac{f}{g})(x)=\frac{2x−3}{x^2−1}.
The domain of this function is {x∣∣x≠±1}.
Exercise \PageIndex{6}
For f(x)=x^2+3 and g(x)=2x−5, find (f/g)(x) and state its domain.
- Hint
-
The new function (f/g)(x)(f/g)(x) is a quotient of two functions. For what values of x is the denominator zero?
- Answer
-
(\frac{f}{g})(x)=\frac{x^2+3}{2x−5}. The domain is {x|x≠\frac{5}{2}}.
Function Composition
When we compose functions, we take a function of a function. For example, suppose the temperature T on a given day is described as a function of time t (measured in hours after midnight) as in Table. Suppose the cost C, to heat or cool a building for 1 hour, can be described as a function of the temperature T. Combining these two functions, we can describe the cost of heating or cooling a building as a function of time by evaluating C(T(t)). We have defined a new function, denoted C∘T, which is defined such that (C∘T)(t)=C(T(t)) for all t in the domain of T. This new function is called a composite function. We note that since cost is a function of temperature and temperature is a function of time, it makes sense to define this new function (C∘T)(t). It does not make sense to consider (T∘C)(t), because temperature is not a function of cost.
Definition: Composite Functions
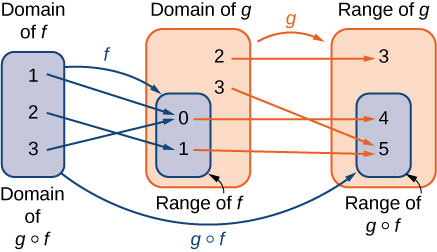
Consider the function f with domain A and range B, and the function g with domain D and range E. If B is a subset of D, then the composite function (g∘f)(x) is the function with domain A such that
(g∘f)(x)=g(f(x))
A composite function g∘f can be viewed in two steps. First, the function f maps each input x in the domain of f to its output f(x) in the range of f. Second, since the range of f is a subset of the domain of g, the output f(x) is an element in the domain of g, and therefore it is mapped to an output g(f(x)) in the range of g. In Figure \PageIndex{11}, we see a visual image of a composite function.
Example \PageIndex{7}: Compositions of Functions Defined by Formulas
Consider the functions f(x)=x^2+1 and g(x)=1/x.
- Find (g∘f)(x) and state its domain and range.
- Evaluate (g∘f)(4),(g∘f)(−1/2).
- Find (f∘g)(x) and state its domain and range.
- Evaluate (f∘g)(4), (f∘g)(−1/2).
Solution
1. We can find the formula for (g∘f)(x) in two different ways. We could write
(g∘f)(x)=g(f(x))=g(x^2+1)=\frac{1}{x^2+1}.
Alternatively, we could write
(g∘f)(x)=g(f(x))=\frac{1}{f(x)}=\frac{1}{x^2+1}.
Since x^2+1≠0 for all real numbers x, the domain of (g∘f)(x) is the set of all real numbers. Since 0<1/(x2+1)≤1, the range is, at most, the interval (0,1]. To show that the range is this entire interval, we let y=1/(x2+1) and solve this equation for x to show that for all y in the interval (0,1], there exists a real number x such that y=1/(x^2+1). Solving this equation for x, we see that x^2+1=1/y, which implies that
x=±\sqrt{\frac{1}{y}−1}
If y is in the interval (0,1], the expression under the radical is nonnegative, and therefore there exists a real number x such that 1/(x^2+1)=y. We conclude that the range of g∘f is the interval (0,1].
2. (g∘f)(4)=g(f(4))=g(4^2+1)=g(17)=\frac{1}{17}
(g∘f)(−\frac{1}{2})=g(f(−\frac{1}{2}))=g((−\frac{1}{2})^2+1)=g(\frac{5}{4})=\frac{4}{5}
3. We can find a formula for (f∘g)(x) in two ways. First, we could write
(f∘g)(x)=f(g(x))=f(\frac{1}{x})=(\frac{1}{x})^2+1.
Alternatively, we could write
(f∘g)(x)=f(g(x))=(g(x))^2+1=(\frac{1}{x})^2+1.
The domain of f∘g is the set of all real numbers x such that x≠0. To find the range of f, we need to find all values y for which there exists a real number x≠0 such that
(\frac{1}{x})^2+1=y.
Solving this equation for x, we see that we need x to satisfy
(\frac{1}{x})^2=y−1,
which simplifies to
\frac{1}{x}=±\sqrt{y−1}
Finally, we obtain
x=±\frac{1}{\sqrt{y−1}}.
Since 1/\sqrt{y−1} is a real number if and only if y>1, the range of f is the set {y∣∣y≥1}.
4.(f∘g)(4)=f(g(4))=f(\frac{1}{4})=(\frac{1}{4})^2+1=\frac{17}{16}
(f∘g)(−\frac{1}{2})=f(g(−\frac{1}{2}))=f(−2)=(−2)^2+1=5
In Example, we can see that (f∘g)(x)≠(g∘f)(x). This tells us, in general terms, that the order in which we compose functions matters.
Exercise \PageIndex{7}
Let f(x)=2−5x. Let g(x)=\sqrt{x}. Find (f∘g)(x).
Solution
(f∘g)(x)=2−5\sqrt{x}.
Example \PageIndex{8}: Composition of Functions Defined by Tables
Consider the functions f and g described by
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|---|---|---|
| f(x) | 0 | 4 | 2 | 4 | -2 | 0 | -2 | 4 |
| x | -4 | -2 | 0 | 2 | 4 |
|---|---|---|---|---|---|
| g(x) | 1 | 0 | 3 | 0 | 5 |
- Evaluate (g∘f)(3),(g∘f)(0).
- State the domain and range of (g∘f)(x).
- Evaluate (f∘f)(3),(f∘f)(1).
- State the domain and range of (f∘f)(x).
Solution:
1. (g∘f)(3)=g(f(3))=g(−2)=0
(g∘f)(0)=g(4)=5
2.The domain of g∘f is the set {−3,−2,−1,0,1,2,3,4}. Since the range of f is the set {−2,0,2,4}, the range of g∘f is the set {0,3,5}.
3. (f∘f)(3)=f(f(3))=f(−2)=4
(f∘f)(1)=f(f(1))=f(−2)=4
4.The domain of f∘f is the set {−3,−2,−1,0,1,2,3,4}. Since the range of f is the set {−2,0,2,4}, the range of f∘f is the set {0,4}.
Example \PageIndex{9}: Application Involving a Composite Function
A store is advertising a sale of 20% off all merchandise. Caroline has a coupon that entitles her to an additional 15% off any item, including sale merchandise. If Caroline decides to purchase an item with an original price of x dollars, how much will she end up paying if she applies her coupon to the sale price? Solve this problem by using a composite function.
Solution
Since the sale price is 20% off the original price, if an item is x dollars, its sale price is given by f(x)=0.80x. Since the coupon entitles an individual to 15% off the price of any item, if an item is y dollars, the price, after applying the coupon, is given by g(y)=0.85y. Therefore, if the price is originally x dollars, its sale price will be f(x)=0.80x and then its final price after the coupon will be g(f(x))=0.85(0.80x)=0.68x.
Exercise \PageIndex{9}
If items are on sale for 10% off their original price, and a customer has a coupon for an additional 30% off, what will be the final price for an item that is originally x dollars, after applying the coupon to the sale price?
Hint
The sale price of an item with an original price of x dollars is f(x)=0.90x. The coupon price for an item that is y dollars is g(y)=0.70y.
Solution
(g∘f)(x)=0.63x
Symmetry of Functions
The graphs of certain functions have symmetry properties that help us understand the function and the shape of its graph. For example, consider the function f(x)=x^4−2x^2−3 shown in Figure \PageIndex{12a}. If we take the part of the curve that lies to the right of the y-axis and flip it over the y-axis, it lays exactly on top of the curve to the left of the y-axis. In this case, we say the function has symmetry about the y-axis. On the other hand, consider the function f(x)=x^3−4x shown in Figure \PageIndex{12b}. If we take the graph and rotate it 180° about the origin, the new graph will look exactly the same. In this case, we say the function has symmetry about the origin.
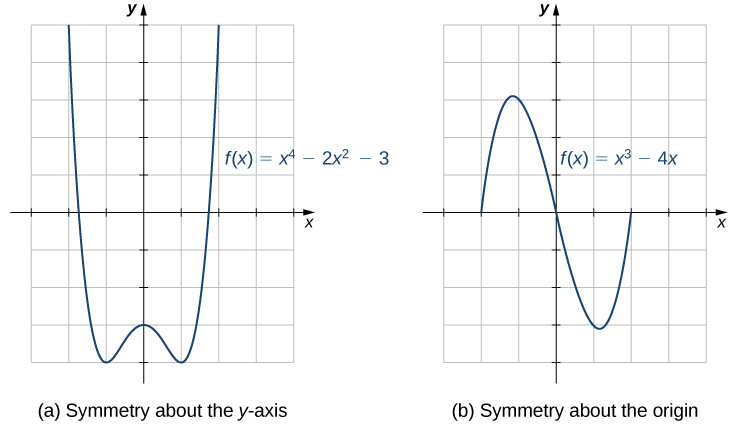
If we are given the graph of a function, it is easy to see whether the graph has one of these symmetry properties. But without a graph, how can we determine algebraically whether a function f has symmetry? Looking at Figure again, we see that since f is symmetric about the y-axis, if the point (x,y) is on the graph, the point (−x,y) is on the graph. In other words, f(−x)=f(x). If a function f has this property, we say f is an even function, which has symmetry about the y-axis. For example, f(x)=x^2 is even because
f(−x)=(−x)^2=x^2=f(x).
In contrast, looking at Figure again, if a function f is symmetric about the origin, then whenever the point (x,y) is on the graph, the point (−x,−y) is also on the graph. In other words, f(−x)=−f(x). If f has this property, we say f is an odd function, which has symmetry about the origin. For example, f(x)=x^3 is odd because
f(−x)=(−x)^3=−x^3=−f(x).
Definition: Even and Odd Functions
- If f(x)=f(−x) for all x in the domain of f, then f is an even function. An even function is symmetric about the y-axis.
- If f(−x)=−f(x) for all x in the domain of f, then f is an odd function. An odd function is symmetric about the origin.
Example \PageIndex{10}: Even and Odd Functions
Determine whether each of the following functions is even, odd, or neither.
- f(x)=−5x^4+7x^2−2
- f(x)=2x^5−4x+5
- f(x)=\frac{3x}{x^2+1}
Solution
To determine whether a function is even or odd, we evaluate f(−x) and compare it to f(x) and −f(x).
1. f(−x)=−5(−x)^4+7(−x)^2−2=−5x^4+7x^2−2=f(x). Therefore, f is even.
2.f(−x)=2(−x)^5−4(−x)+5=−2x^5+4x+5. Now, f(−x)≠f(x). Furthermore, noting that −f(x)=−2x^5+4x−5, we see that f(−x)≠−f(x). Therefore, f is neither even nor odd.
3.f(−x)=3(−x)/((−x)2+1)=−3x/(x^2+1)=−[3x/(x^2+1)]=−f(x). Therefore, f is odd.
Exercise \PageIndex{10}
Determine whether f(x)=4x^3−5x is even, odd, or neither.
- Hint
-
Compare f(−x) with f(x) and −f(x).
- Answer
-
f(x)is odd.
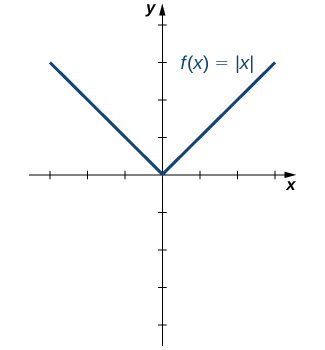
One symmetric function that arises frequently is the absolute value function, written as |x|. The absolute value function is defined as
f(x)=\begin{cases} -x& x<0 \\ x& x≥0 \end{cases}
Some students describe this function by stating that it “makes everything positive.” By the definition of the absolute value function, we see that if x<0, then |x|=−x>0, and if x>0, then |x|=x>0. However, for x=0,|x|=0. Therefore, it is more accurate to say that for all nonzero inputs, the output is positive, but if x=0, the output |x|=0. We conclude that the range of the absolute value function is {y|y≥0}. In Figure \PageIndex{13}, we see that the absolute value function is symmetric about the y-axis and is therefore an even function.
Example \PageIndex{11}: Working with the Absolute Value Function
Find the domain and range of the function f(x)=2|x−3|+4.
Solution
Since the absolute value function is defined for all real numbers, the domain of this function is (−∞,∞). Since |x−3|≥0 for all x, the function f(x)=2|x−3|+4≥4. Therefore, the range is, at most, the set {y|y≥4}. To see that the range is, in fact, this whole set, we need to show that for y≥4 there exists a real number x such that
2|x−3|+4=y
A real number x satisfies this equation as long as
|x−3|=\frac{1}{2}(y−4)
Since y≥4, we know y−4≥0, and thus the right-hand side of the equation is nonnegative, so it is possible that there is a solution. Furthermore,
|x−3|=\begin{cases} −(x−3)&\text{if } x<3\\x−3&\text{if } x≥3\end{cases}.
Therefore, we see there are two solutions:
x=±\frac{1}{2}(y−4)+3.
The range of this function is {y|y≥4}.
Exercise \PageIndex{11}: Domain and Range
For the function f(x)=|x+2|−4, find the domain and range.
- Hint
-
|x+2|≥0 for all real numbers x.
- Answer
-
Domain = (−∞,∞), range = {y|y≥−4}.
Real Valued functions
Definition
Let D \subset \mathbb{R}. Then f:D\to \mathbb{R} is said to be a real valued function from D to \mathbb{R} if for each element x \in D, there exists a unique (one and only one) element y \in \mathbb{R}, such that y=f(x). In this case D is called domain of f , x is called an independent variable, and y is called an dependent variable,
Note that we will follow the following convention: for a given real valued function f, the domain of f is denoted by \( D(f) \) and defined by D(f) = the set of all x such that there exists a y \in \mathbb{R} such that y=f(x).
Library of functions
We have studied the general characteristics of functions, so now let’s examine some specific classes of functions. We begin by reviewing the basic properties of linear and quadratic functions, and then generalize to include higher-degree polynomials. By combining root functions with polynomials, we can define general algebraic functions and distinguish them from the transcendental functions we examine later in this chapter. We finish the section with examples of piecewise-defined functions and take a look at how to sketch the graph of a function that has been shifted, stretched, or reflected from its initial form. The following examples of functions will be used in this course:
Linear Functions and Slope
The easiest type of function to consider is a linear function. Linear functions have the form f(x)=ax+b, where a and b are constants. In Figure \PageIndex{1}, we see examples of linear functions when a is positive, negative, and zero. Note that if a>0, the graph of the line rises as x increases. In other words, f(x)=ax+b is increasing on (−∞, ∞). If a<0, the graph of the line falls as x increases. In this case, f(x)=ax+b is decreasing on (−∞, ∞). If a=0, the line is horizontal.
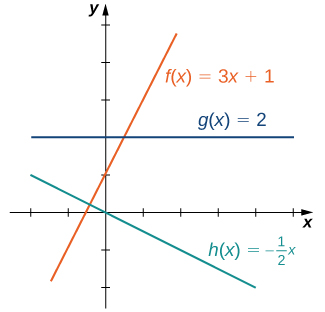
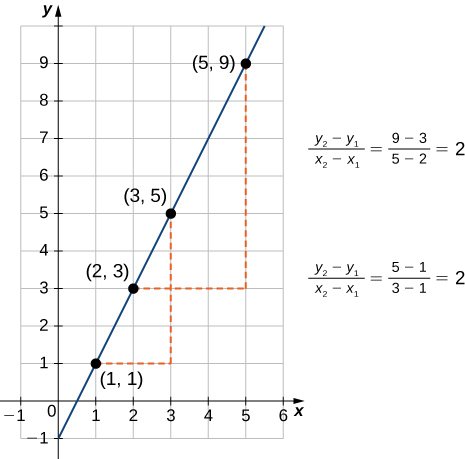
As suggested by Figure, the graph of any linear function is a line. One of the distinguishing features of a line is its slope. The slope is the change in y for each unit change in x. The slope measures both the steepness and the direction of a line. If the slope is positive, the line points upward when moving from left to right. If the slope is negative, the line points downward when moving from left to right. If the slope is zero, the line is horizontal. To calculate the slope of a line, we need to determine the ratio of the change in y versus the change in x. To do so, we choose any two points (x_1,y_1) and (x_2,y_2) on the line and calculate \dfrac{y_2−y_1}{x_2−x_1}. In Figure \PageIndex{2}, we see this ratio is independent of the points chosen.
Definition: Linear Functions
Consider line L passing through points (x_1,y_1) and (x_2,y_2). Let Δy=y_2−y_1 and Δx=x_2−x_1 denote the changes in y and x,respectively. The slope of the line is
m=\dfrac{y_2−y_1}{x_2−x_1}=\dfrac{Δy}{Δx}
We now examine the relationship between slope and the formula for a linear function. Consider the linear function given by the formula f(x)=ax+b. As discussed earlier, we know the graph of a linear function is given by a line. We can use our definition of slope to calculate the slope of this line. As shown, we can determine the slope by calculating (y_2−y_1)/(x_2−x_1) for any points (x_1,y_1) and (x_2,y_2) on the line. Evaluating the function f at x=0, we see that (0,b) is a point on this line. Evaluating this function at x=1, we see that (1,a+b) is also a point on this line. Therefore, the slope of this line is
\dfrac{(a+b)−b}{1−0}=a.
We have shown that the coefficient a is the slope of the line. We can conclude that the formula f(x)=ax+b describes a line with slope a. Furthermore, because this line intersects the y-axis at the point (0,b), we see that the y-intercept for this linear function is (0,b). We conclude that the formula f(x)=ax+b tells us the slope, a, and the y-intercept, (0,b), for this line. Since we often use the symbol m to denote the slope of a line, we can write
\underbrace{f(x)=mx+b}_{\text{slope-intercept form}}
to denote the slope-intercept form of a linear function.
Sometimes it is convenient to express a linear function in different ways. For example, suppose the graph of a linear function passes through the point (x_1,y_1) and the slope of the line is m. Since any other point (x,f(x)) on the graph of f must satisfy the equation
m=\dfrac{f(x)−y_1}{x−x_1},
this linear function can be expressed by writing
\underbrace{f(x)−y_1=m(x−x_1)}_{\text{point-slope equation}}.
We call this equation the point-slope equation for that linear function.
Since every nonvertical line is the graph of a linear function, the points on a nonvertical line can be described using the slope-intercept or point-slope equations. However, a vertical line does not represent the graph of a function and cannot be expressed in either of these forms. Instead, a vertical line is described by the equation x=k for some constant k. Since neither the slope-intercept form nor the point-slope form allows for vertical lines, we use the notation
\underbrace{ax+by=c}_{\text{standard form}},
where a,b are both not zero, to denote the standard form of a line.
Definition: point-slope equation, point-slope equation and the standard form of a line
Consider a line passing through the point (x_1,y_1) with slope m. The equation
y−y_1=m(x−x_1)
is the point-slope equation for that line.
Consider a line with slope m and y-intercept (0,b). The equation
y=mx+b
is an equation for that line in point-slope equation.
The standard form of a line is given by the equation
ax+by=c,
where a and b are both not zero. This form is more general because it allows for a vertical line, x=k.
Example \PageIndex{1}: Finding the Slope and Equations of Lines
Consider the line passing through the points (11,−4) and (−4,5), as shown in Figure.
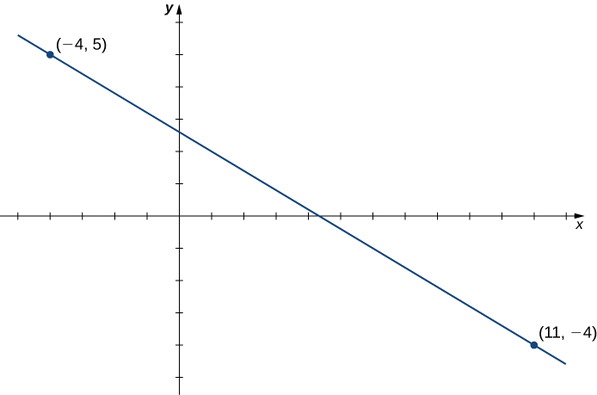
- Find the slope of the line.
- Find an equation for this linear function in point-slope form.
- Find an equation for this linear function in slope-intercept form.
Solution
1. The slope of the line is
m=\dfrac{y_2−y_1}{x_2−x_1}=\dfrac{5−(−4)}{−4−11}=−\dfrac{9}{15}=−\dfrac{3}{5}. \nonumber
2. To find an equation for the linear function in point-slope form, use the slope m=−3/5 and choose any point on the line. If we choose the point (11,−4), we get the equation
f(x)+4=−\dfrac{3}{5}(x−11). \nonumber
3. To find an equation for the linear function in slope-intercept form, solve the equation in part b. for f(x). When we do this, we get the equation
f(x)=−\dfrac{3}{5}x+\dfrac{13}{5}. \nonumber
Exercise \PageIndex{1}
Consider the line passing through points (−3,2) and (1,4).
- Find the slope of the line.
- Find an equation of that line in point-slope form.
- Find an equation of that line in slope-intercept form.
- Hint
-
The slope m=Δy/Δx.
- Answer a
-
m=1/2.
- Answer b
-
The point-slope form is y−4=\dfrac{1}{2}(x−1).
- Answer c
-
The slope-intercept form is y=\dfrac{1}{2}x+\dfrac{7}{2}.
Example \PageIndex{2}:
Jessica leaves her house at 5:50 a.m. and goes for a 9-mile run. She returns to her house at 7:08 a.m. Answer the following questions, assuming Jessica runs at a constant pace.
- Describe the distance D (in miles) Jessica runs as a linear function of her run time t (in minutes).
- Sketch a graph of D.
- Interpret the meaning of the slope.
Solution
a. At time t=0, Jessica is at her house, so D(0)=0. At time t=78 minutes, Jessica has finished running 9 mi, so D(78)=9. The slope of the linear function is
m=\dfrac{9−0}{78−0}=\dfrac{3}{26}.\nonumber
The y-intercept is (0,0), so the equation for this linear function is
D(t)=\dfrac{3}{26}t. \nonumber
b. To graph D, use the fact that the graph passes through the origin and has slope m=3/26.
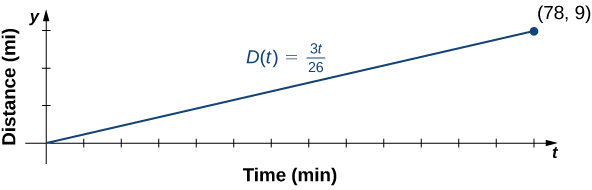
c. The slope m=3/26≈0.115 describes the distance (in miles) Jessica runs per minute, or her average velocity.
Example \PageIndex{1}
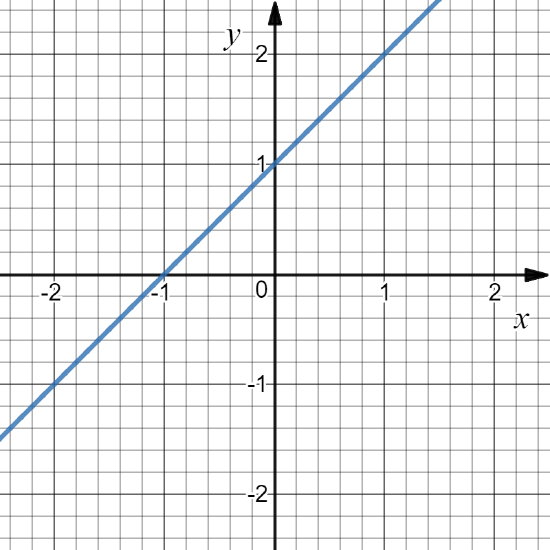
Define f: \mathbb{R}\to \mathbb{R} by f(x)=x+1. Then D(f) = \mathbb{R} .
Exercise \PageIndex{3}
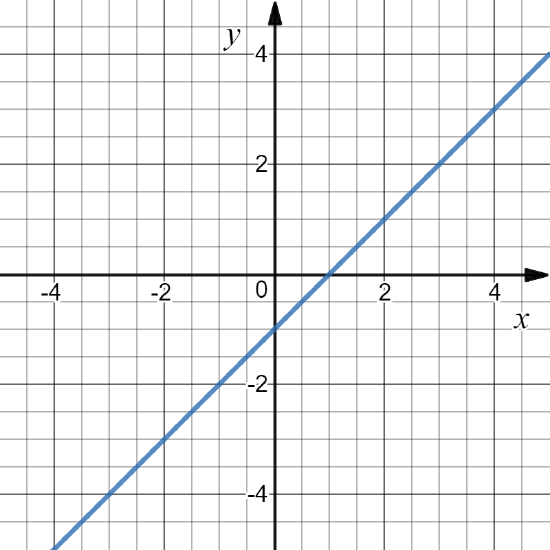
Define f: \mathbb{R}\to \mathbb{R} by f(x)=x-1. Find the domain.
- Answer
-
D(f) = \mathbb{R}
\rm I\!R
Polynomials
A linear function is a special type of a more general class of functions: polynomials. A polynomial function is any function that can be written in the form
f(x)=a_nx^n+a_{n−1}x^{n−1}+…+a_1x+a_0
for some integer n≥0 and constants a_n,a+{n−1},…,a_0, where a_n≠0. In the case when n=0, we allow for a_0=0; if a_0=0, the function f(x)=0 is called the zero function. The value n is called the degree of the polynomial; the constant an is called the leading coefficient. A linear function of the form f(x)=mx+b is a polynomial of degree 1 if m≠0 and degree 0 if m=0. A polynomial of degree 0 is also called a constant function. A polynomial function of degree 2 is called a quadratic function. In particular, a quadratic function has the form
f(x)=ax^2+bx+c,
where a≠0. A polynomial function of degree 3 is called a cubic function.
Power Functions
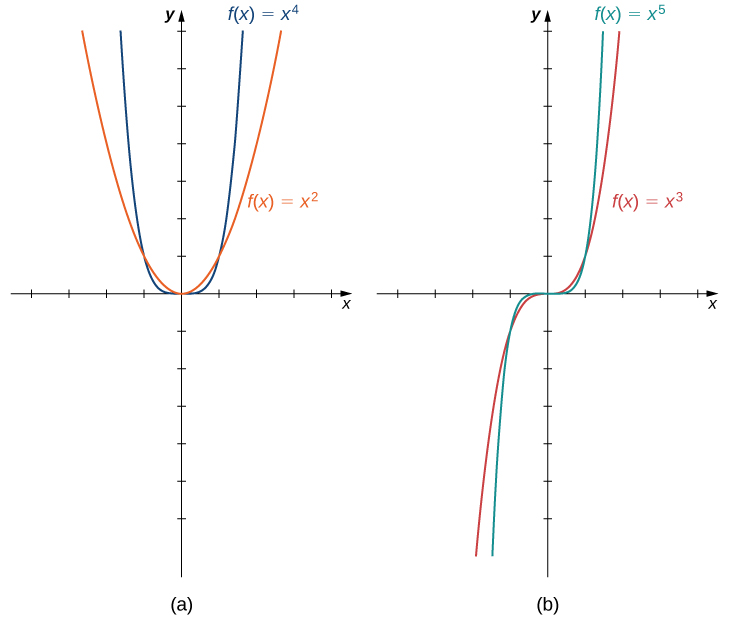
Some polynomial functions are power functions. A power function is any function of the form f(x)=ax^b, where a and b are any real numbers. The exponent in a power function can be any real number, but here we consider the case when the exponent is a positive integer. (We consider other cases later.) If the exponent is a positive integer, then f(x)=ax^n is a polynomial. If n is even, then f(x)=ax^n is an even function because f(−x)=a(−x)^n=ax^n if n is even. If n is odd, then f(x)=ax^n is an odd function because f(−x)=a(−x)^n=−ax^n if n is odd (Figure \PageIndex{3}).
Quadratic functions
Example \PageIndex{2}:
Define f: \mathbb{R}\to \mathbb{R} by f(x)=x^2. Then D(f) = \mathbb{R} .
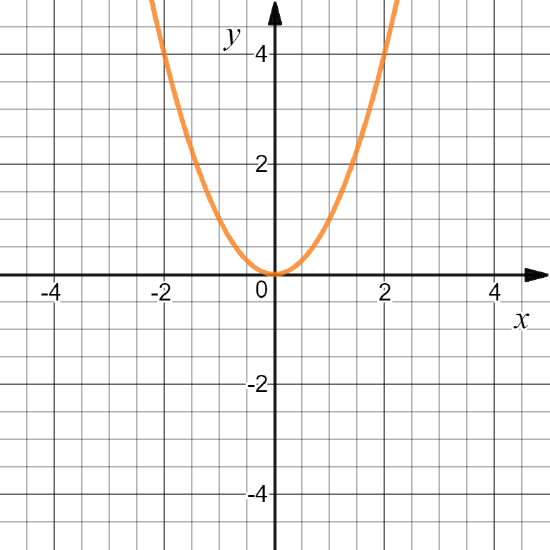
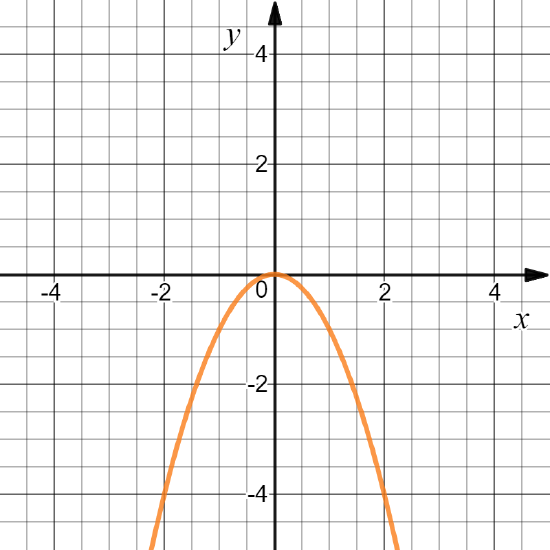
Exercise \PageIndex{2}
Define f: \mathbb{R}\to \mathbb{R} by f(x)=-x^2. Find the domain.
- Answer
- D(f) = \mathbb{R}
Cubic functions
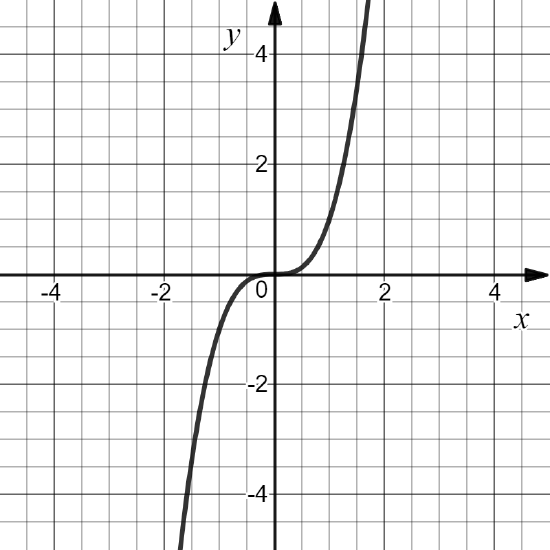
Example \PageIndex{3}:
Define f: \mathbb{R}\to \mathbb{R} by f(x)=x^3. Then D(f) = \mathbb{R} .
.
Exercise \PageIndex{3}
Define f: \mathbb{R}\to \mathbb{R} by f(x)=x^3. Find the Domain
- Answer
-
D(f) = \mathbb{R}
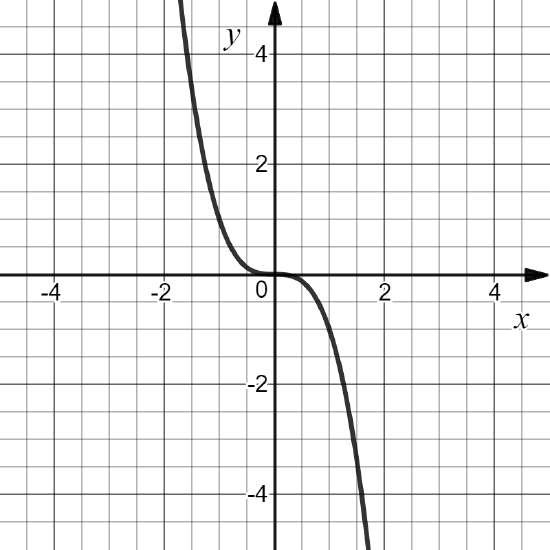
Algebraic Functions
By allowing for quotients and fractional powers in polynomial functions, we create a larger class of functions. An algebraic function is one that involves addition, subtraction, multiplication, division, rational powers, and roots. Two types of algebraic functions are rational functions and root functions.
Just as rational numbers are quotients of integers, rational functions are quotients of polynomials. In particular, a rational function is any function of the form f(x)=p(x)/q(x),where p(x) and q(x) are polynomials. For example,
f(x)=\dfrac{3x−1}{5x+2} and g(x)=\dfrac{4}{x^2+1}
are rational functions. A root function is a power function of the form f(x)=x^{1/n}, where n is a positive integer greater than one. For example, f(x)=x1/2=x√ is the square-root function and g(x)=x^{1/3}=\sqrt[3]{x}) is the cube-root function. By allowing for compositions of root functions and rational functions, we can create other algebraic functions. For example, f(x)=\sqrt{4−x^2} is an algebraic function.
Example \PageIndex{5}: Finding Domain and Range for Algebraic Functions
For each of the following functions, find the domain and range.
- f(x)=\dfrac{3x−1}{5x+2}
- f(x)=\sqrt{4−x^2}
Solution
1.It is not possible to divide by zero, so the domain is the set of real numbers x such that x≠−2/5. To find the range, we need to find the values y for which there exists a real number x such that
y=\dfrac{3x−1}{5x+2}
When we multiply both sides of this equation by 5x+2, we see that x must satisfy the equation
5xy+2y=3x−1.
From this equation, we can see that x must satisfy
2y+1=x(3−5y).
If y=3/5, this equation has no solution. On the other hand, as long as y≠3/5,
x=\dfrac{2y+1}{3−5y}
satisfies this equation. We can conclude that the range of f is {y|y≠3/5}.
2. To find the domain of f, we need 4−x^2≥0. When we factor, we write 4−x^2=(2−x)(2+x)≥0. This inequality holds if and only if both terms are positive or both terms are negative. For both terms to be positive, we need to find x such that
2−x≥0 and 2+x≥0.
These two inequalities reduce to 2≥x and x≥−2. Therefore, the set {x|−2≤x≤2} must be part of the domain. For both terms to be negative, we need
2−x≤0 and 2+x≥0.
These two inequalities also reduce to 2≤x and x≥−2. There are no values of x that satisfy both of these inequalities. Thus, we can conclude the domain of this function is {x|−2≤x≤2}.
If −2≤x≤2, then 0≤4−x^2≤4. Therefore, 0≤\sqrt{4−x2}≤2, and the range of f is {y|0≤y≤2}.
Exercise \PageIndex{3}
Find the domain and range for the function f(x)=(5x+2)/(2x−1).
- Hint
-
The denominator cannot be zero. Solve the equation y=(5x+2)/(2x−1) for x to find the range.
- Answer
-
The domain is the set of real numbers x such that x≠1/2. The range is the set \{y|y≠5/2\}.
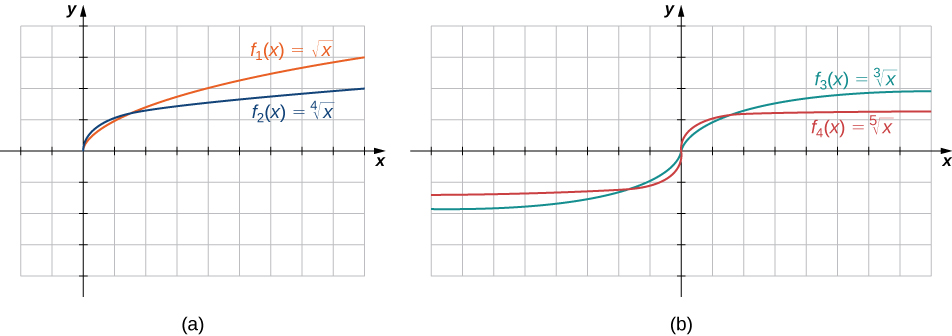
The root functions f(x)=x^{1/n} have defining characteristics depending on whether n is odd or even. For all even integers n≥2, the domain of f(x)=x^{1/n} is the interval [0,∞). For all odd integers n≥1, the domain of f(x)=x^{1/n} is the set of all real numbers. Since x^{1/n}=(−x)^{1/n} for odd integers n,f(x)=x^{1/n} is an odd function ifn is odd. See the graphs of root functions for different values of n in Figure.
Example \PageIndex{6}: Finding Domains for Algebraic Functions
For each of the following functions, determine the domain of the function.
- f(x)=\dfrac{3}{x^2−1}
- f(x)=\dfrac{2x+5}{3x^2+4}
- f(x)=\sqrt{4−3x}
- f(x)=\sqrt[3]{2x−1}
Solution
- You cannot divide by zero, so the domain is the set of values x such that x^2−1≠0. Therefore, the domain is {x|x≠±1}.
- You need to determine the values of x for which the denominator is zero. Since 3x^2+4≥4 for all real numbers x, the denominator is never zero. Therefore, the domain is (−∞,∞).
- Since the square root of a negative number is not a real number, the domain is the set of values x for which 4−3x≥0. Therefore, the domain is {x|x≤4/3}.
- The cube root is defined for all real numbers, so the domain is the interval (−∞, ∞).
Exercise \PageIndex{4}
Find the domain for each of the following functions: f(x)=(5−2x)/(x^2+2) and g(x)=\sqrt{5x−1}.
- Hint
-
Determine the values of x when the expression in the denominator of f is nonzero, and find the values of x when the expression inside the radical of g is nonnegative.
- Answer
-
The domain of f is (−∞, ∞). The domain of g is {x|x≥1/5}.
Transcendental Functions
Thus far, we have discussed algebraic functions. Some functions, however, cannot be described by basic algebraic operations. These functions are known as transcendental functions because they are said to “transcend,” or go beyond, algebra. The most common transcendental functions are trigonometric, exponential, and logarithmic functions. A trigonometric function relates the ratios of two sides of a right triangle. They are sinx, cosx, tanx, cotx, secx, and cscx. (We discuss trigonometric functions later in the chapter.) An exponential function is a function of the form f(x)=b^x, where the base b>0,b≠1. A logarithmic function is a function of the form f(x)=log_b(x) for some constant b>0,b≠1, where log_b(x)=y if and only if b^y=x. (We also discuss exponential and logarithmic functions later in the chapter.)
Example \PageIndex{7}: Classifying Algebraic and Transcendental Functions
Classify each of the following functions, a. through c., as algebraic or transcendental.
- f(x)=\dfrac{\sqrt{x^3+1}}{4x+2}
- f(x)=2^{x^2}
- f(x)=\sin(2x)
Solution
- Since this function involves basic algebraic operations only, it is an algebraic function.
- This function cannot be written as a formula that involves only basic algebraic operations, so it is transcendental. (Note that algebraic functions can only have powers that are rational numbers.)
- As in part b, this function cannot be written using a formula involving basic algebraic operations only; therefore, this function is transcendental.
Exercise \PageIndex{5}:
Is f(x)=x/2 an algebraic or a transcendental function?
- Answer
-
Algebraic
Piecewise-Defined Functions
Sometimes a function is defined by different formulas on different parts of its domain. A function with this property is known as a piecewise-defined function. The absolute value function is an example of a piecewise-defined function because the formula changes with the sign of x:
f(x)=\begin{cases}−x & x<0\\x & x≥0\end{cases}.
Other piecewise-defined functions may be represented by completely different formulas, depending on the part of the domain in which a point falls. To graph a piecewise-defined function, we graph each part of the function in its respective domain, on the same coordinate system. If the formula for a function is different for x<a and x>a, we need to pay special attention to what happens at x=a when we graph the function. Sometimes the graph needs to include an open or closed circle to indicate the value of the function at x=a. We examine this in the next example.
Example \PageIndex{8}: Graphing a Piecewise-Defined Function
Sketch a graph of the following piecewise-defined function:
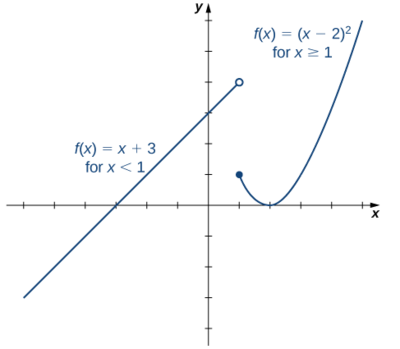
f(x)=\begin{cases}x+3,&x<1\\(x−2)^2,&x≥1\end{cases}.
Solution
Graph the linear function y=x+3 on the interval (−∞,1) and graph the quadratic function y=(x−2)^2 on the interval [1,∞). Since the value of the function at x=1 is given by the formula f(x)=(x−2)^2, we see that f(1)=1. To indicate this on the graph, we draw a closed circle at the point (1,1). The value of the function is given by f(x)=x+2 for all x<1, but not at x=1. To indicate this on the graph, we draw an open circle at (1,4).
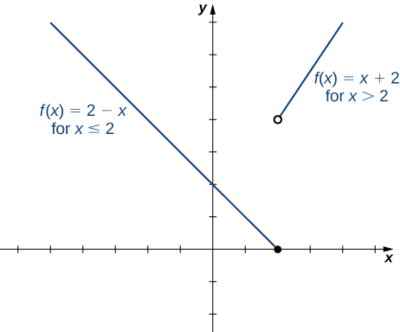
2) Sketch a graph of the function
f(x)=\begin{cases}2−x,&x≤2\\x+2,&x>2\end{cases}.
Solution:
Example \PageIndex{9}: Parking Fees Described by a Piecewise-Defined Function
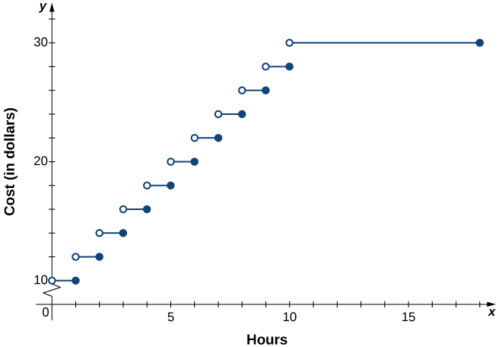
In a big city, drivers are charged variable rates for parking in a parking garage. They are charged $10 for the first hour or any part of the first hour and an additional $2 for each hour or part thereof up to a maximum of $30 for the day. The parking garage is open from 6 a.m. to 12 midnight.
- Write a piecewise-defined function that describes the cost C to park in the parking garage as a function of hours parked x.
- Sketch a graph of this function C(x).
Solution
1.Since the parking garage is open 18 hours each day, the domain for this function is {x|0<x≤18}. The cost to park a car at this parking garage can be described piecewise by the function
C(x)=\begin{cases}10,&0<x≤1\\12,&1<x≤2\\14,&2<x≤3\\16,&3<x≤4\\ ⋮\\30,&10<x≤18\end{cases}.
2.The graph of the function consists of several horizontal line segments.
Exercise \PageIndex{6}
The cost of mailing a letter is a function of the weight of the letter. Suppose the cost of mailing a letter is 49¢ for the first ounce and 21¢ for each additional ounce. Write a piecewise-defined function describing the cost C as a function of the weight x for 0<x≤3, where C is measured in cents and x is measured in ounces.
- Hint
-
The piecewise-defined function is constant on the intervals (0,1],(1,2],….
- Answer
-
C(x)=\begin{cases}49,&0<x≤1\\70,&1<x≤2\\91,&2<x≤3\end{cases}
Transformations of Functions
We have seen several cases in which we have added, subtracted, or multiplied constants to form variations of simple functions. In the previous example, for instance, we subtracted 2 from the argument of the function y=x^2 to get the function f(x)=(x−2)^2. This subtraction represents a shift of the function y=x^2 two units to the right. A shift, horizontally or vertically, is a type of transformation of a function. Other transformations include horizontal and vertical scalings, and reflections about the axes.
A vertical shift of a function occurs if we add or subtract the same constant to each output y. For c>0, the graph of f(x)+c is a shift of the graph of f(x) up c units, whereas the graph of f(x)−c is a shift of the graph of f(x) down c units. For example, the graph of the function f(x)=x^3+4 is the graph of y=x^3 shifted up 4 units; the graph of the function f(x)=x^3−4 is the graph of y=x^3 shifted down 4 units (Figure \PageIndex{9}).
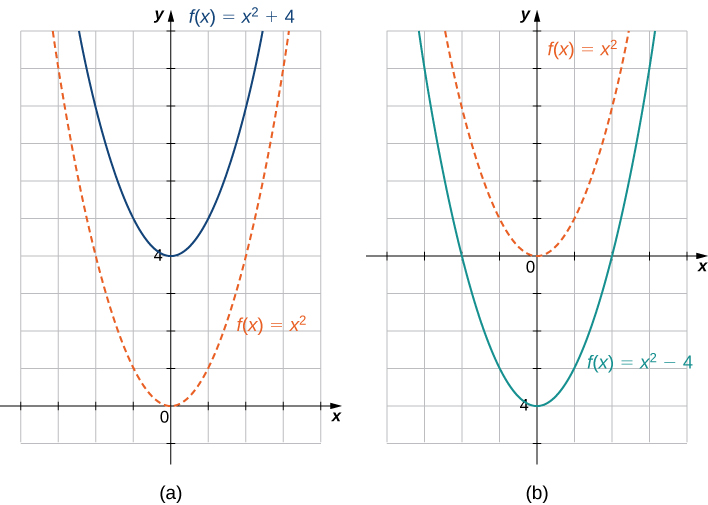
A horizontal shift of a function occurs if we add or subtract the same constant to each input x. For c>0, the graph of f(x+c) is a shift of the graph of f(x) to the left c units; the graph of f(x−c) is a shift of the graph of f(x) to the right c units. Why does the graph shift left when adding a constant and shift right when subtracting a constant? To answer this question, let’s look at an example.
Consider the function f(x)=|x+3| and evaluate this function at x−3. Since f(x−3)=|x| and x−3<x, the graph of f(x)=|x+3| is the graph of y=|x| shifted left 3 units. Similarly, the graph of f(x)=|x−3| is the graph of y=|x| shifted right 3 units (Figure \PageIndex{10}).
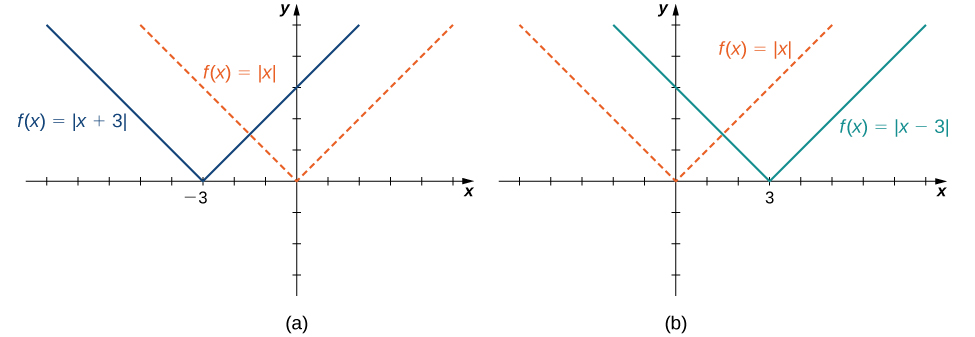
A vertical scaling of a graph occurs if we multiply all outputs y of a function by the same positive constant. For c>0, the graph of the function cf(x) is the graph of f(x) scaled vertically by a factor of c. If c>1, the values of the outputs for the function cf(x) are larger than the values of the outputs for the function f(x); therefore, the graph has been stretched vertically. If 0<c<1, then the outputs of the function cf(x) are smaller, so the graph has been compressed. For example, the graph of the function f(x)=3x^2 is the graph of y=x^2 stretched vertically by a factor of 3, whereas the graph of f(x)=x^2/3 is the graph of y=x^2 compressed vertically by a factor of 3 (Figure \PageIndex{11b}).
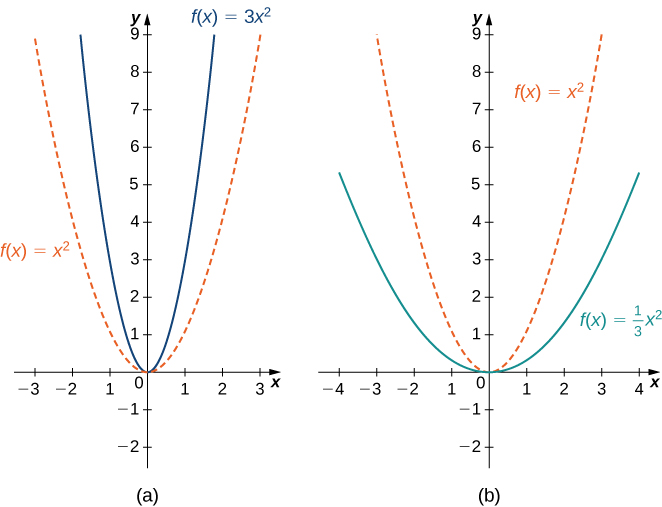
The horizontal scaling of a function occurs if we multiply the inputs x by the same positive constant. For c>0, the graph of the function f(cx) is the graph of f(x) scaled horizontally by a factor of c. If c>1, the graph of f(cx) is the graph of f(x) compressed horizontally. If 0<c<1, the graph of f(cx) is the graph of f(x) stretched horizontally. For example, consider the function f(x)=\sqrt{2x} and evaluate f at x/2. Since f(x/2)=\sqrt{x}, the graph of f(x)=\sqrt{2x} is the graph of y=\sqrt{x} compressed horizontally. The graph of y=\sqrt{x/2} is a horizontal stretch of the graph of y=\sqrt{x} (Figure \PageIndex{12}).
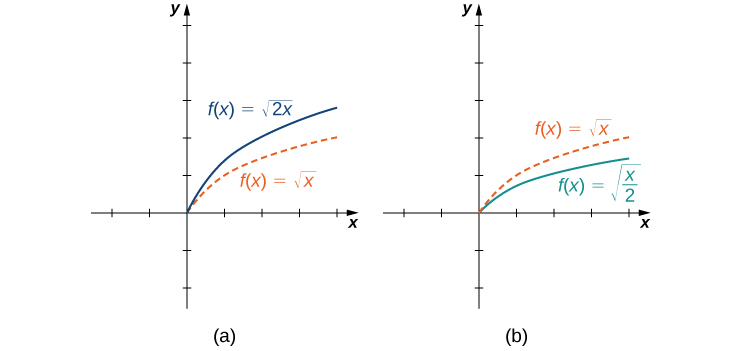
We have explored what happens to the graph of a function f when we multiply f by a constant c>0 to get a new function cf(x). We have also discussed what happens to the graph of a function fwhen we multiply the independent variable x by c>0 to get a new function f(cx). However, we have not addressed what happens to the graph of the function if the constant c is negative. If we have a constant c<0, we can write c as a positive number multiplied by −1; but, what kind of transformation do we get when we multiply the function or its argument by −1? When we multiply all the outputs by −1, we get a reflection about the x-axis. When we multiply all inputs by −1, we get a reflection about the y-axis. For example, the graph of f(x)=−(x^3+1) is the graph of y=(x^3+1) reflected about the x-axis. The graph of f(x)=(−x)^3+1 is the graph of y=x^3+1 reflected about the y-axis (Figure \PageIndex{10}).
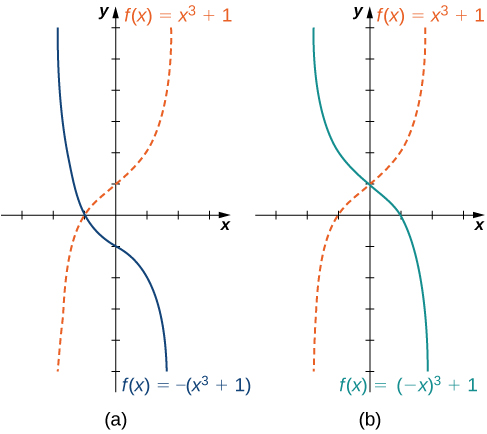
If the graph of a function consists of more than one transformation of another graph, it is important to transform the graph in the correct order. Given a function f(x), the graph of the related function y=cf(a(x+b))+d can be obtained from the graph of y=f(x)by performing the transformations in the following order.
- Horizontal shift of the graph of y=f(x). If b>0, shift left. If b<0 shift right.
- Horizontal scaling of the graph of y=f(x+b) by a factor of |a|. If a<0, reflect the graph about the y-axis.
- Vertical scaling of the graph of y=f(a(x+b)) by a factor of |c|. If c<0, reflect the graph about the x -axis.
- Vertical shift of the graph of y=cf(a(x+b)). If d>0, shift up. If d<0, shift down.
We can summarize the different transformations and their related effects on the graph of a function in the following table.
| Transformation of f (c>0) | Effect of the graph of f |
|---|---|
| f(x)+c | Vertical shift up c units |
| f(x)-c | Vertical shift down c units |
| f(x+c) | Shift left by c units |
| f(x-c) | Shift right by c units |
| cf(x) |
Vertical stretch if c>1; vertical compression if 0<c<1 |
| f(cx) |
Horizontal stretch if 0<c<1; horizontal compression if c>1 |
| -f(x) | Reflection about the x-axis |
| -f(x) | Reflection about the y-axis |
Example \PageIndex{10}: Transforming a Function
For each of the following functions, a. and b., sketch a graph by using a sequence of transformations of a well-known function.
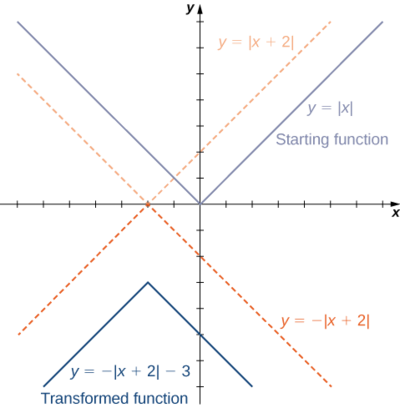
- f(x)=−|x+2|−3
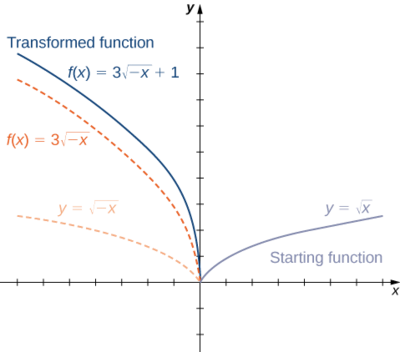
- f(x)=\sqrt[3]{x}+1
Solution
1.Starting with the graph of y=|x|, shift 2 units to the left, reflect about the x-axis, and then shift down 3 units.
2. Starting with the graph of y=x√, reflect about the y-axis, stretch the graph vertically by a factor of 3, and move up 1 unit.
Exercise \PageIndex{7}
Describe how the function f(x)=−(x+1)^2−4 can be graphed using the graph of y=x^2 and a sequence of transformations
- Answer
-
Shift the graph y=x^2 to the left 1 unit, reflect about the x-axis, then shift down 4 units.
Below are some more examples:
More Examples
Rational functions
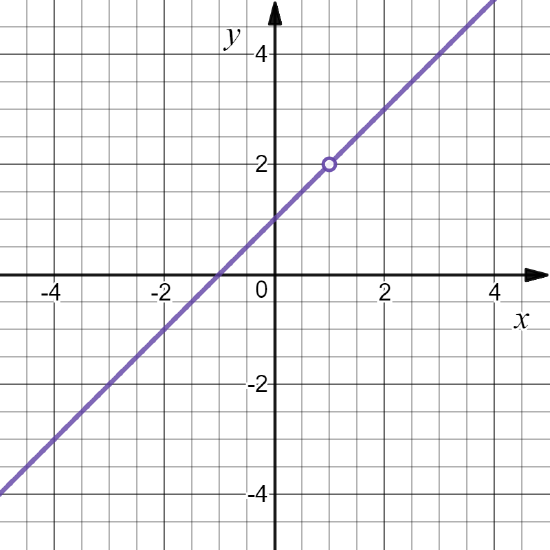
Example \PageIndex{8}
Define f: \mathbb{R}\to \mathbb{R} by f(x)= \displaystyle\frac{x^2-1}{x-1}. Then D(f)= \mathbb{R} \setminus \{1\} .
Exercise \PageIndex{9}
Define f: \mathbb{R}\to \mathbb{R} by f(x)= \displaystyle\frac{x^2-1}{x+1}. Find the domain.
- Answer
-
D(f)= \mathbb{R} \setminus \{-1\}
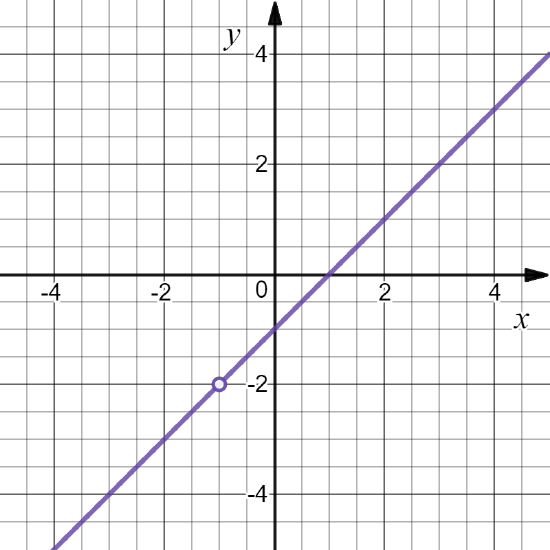
Example \PageIndex{10}:
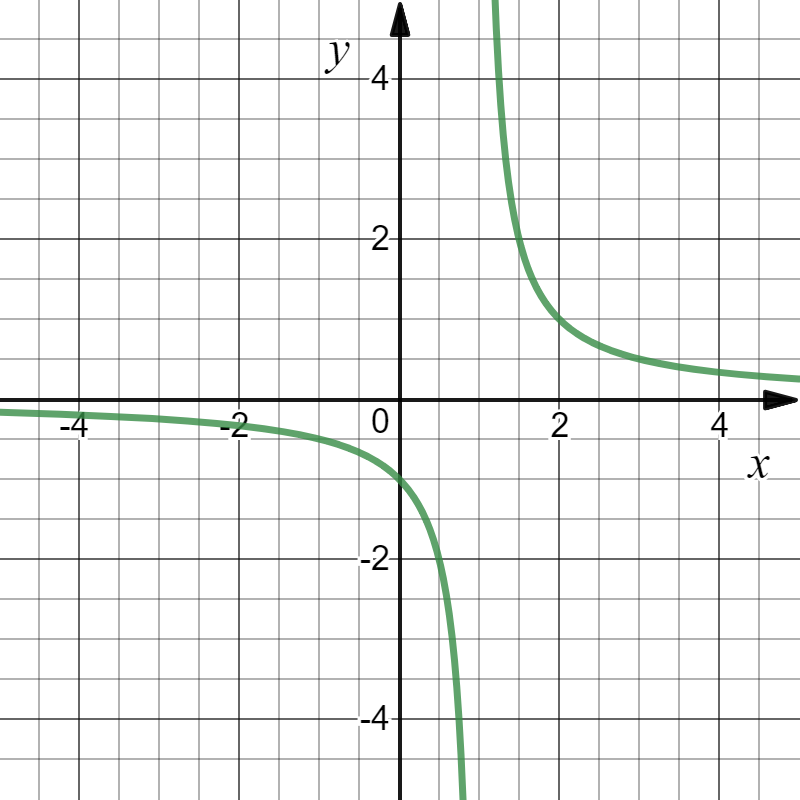
Define f: \mathbb{R}\to \mathbb{R} by f(x)= \displaystyle\frac{1}{x-1}. Then D(f)= \mathbb{R} \setminus \{1\} .
(x-1).png?revision=1&size=bestfit&width=300&height=300)
Exercise \PageIndex{11}
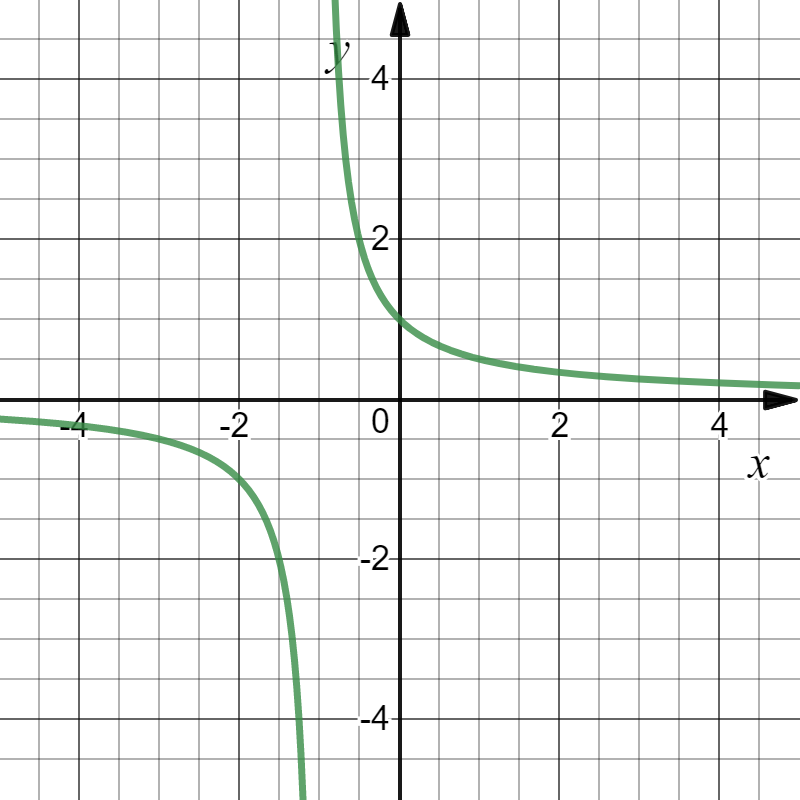
Define f: \mathbb{R}\to \mathbb{R} by f(x)= \displaystyle\frac{1}{x-1}. Find the domain.
- Answer
-
D(f)= \mathbb{R} \setminus \{-1\} .
(x%252B1).png?revision=1&size=bestfit&width=300&height=300)
Irrational functions
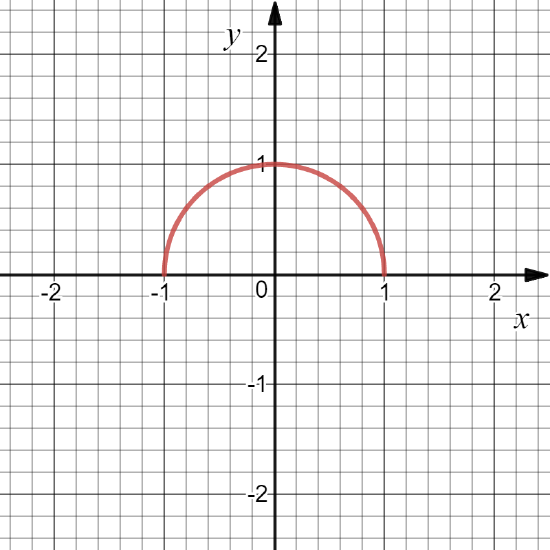
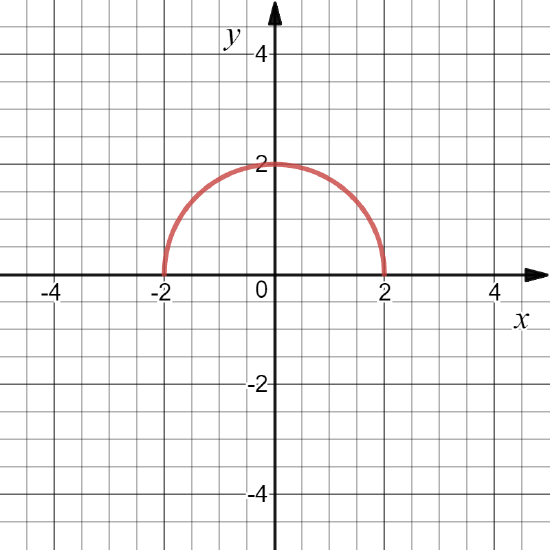
upper half unit circle \PageIndex{12}
Define f: \mathbb{R}\to \mathbb{R} by f(x)=\sqrt{1-x^2}. Then D(f)= [-1,1].
Exercise \PageIndex{13}
Define f: \mathbb{R}\to \mathbb{R} by f(x)=\sqrt{4-x^2}. Find the domain.
- Answer
-
D(f)= [-2,2].
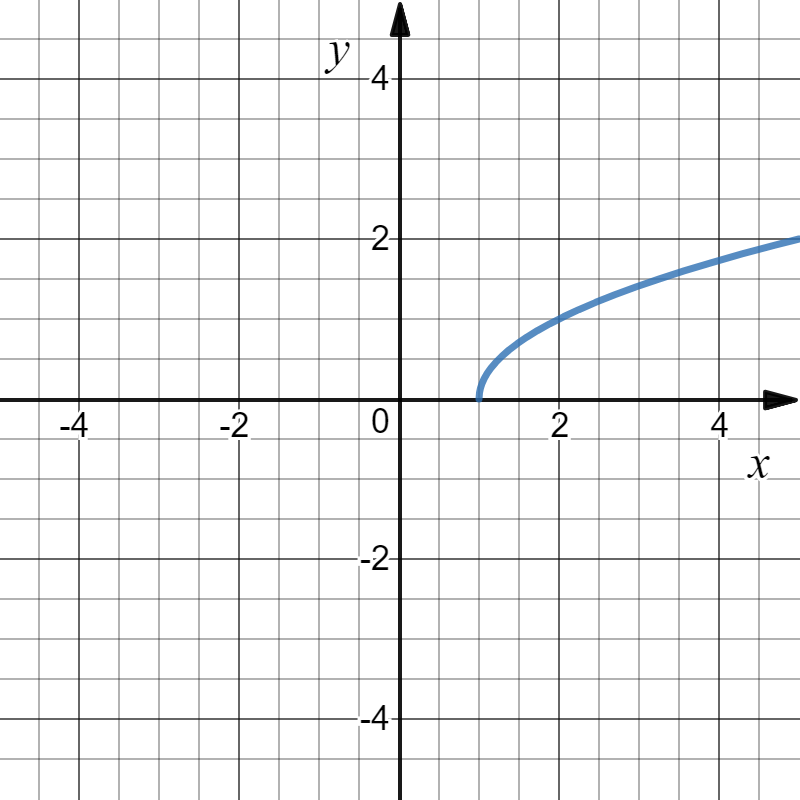
Example \PageIndex{14}:
Define f: \mathbb{R}\to \mathbb{R} by f(x)=\sqrt{1-x}. Then D(f)= [0,\infty) .
.png?revision=1&size=bestfit&width=300&height=300)
Exercise \PageIndex{15}
Define f: \mathbb{R}\to \mathbb{R} by f(x)=\sqrt{1-x}. Find the domain.
- Answer
-
D(f)= [0,\infty)
.png?revision=1&size=bestfit&width=300&height=300)
Piecewise-defined function
Absolute valued function
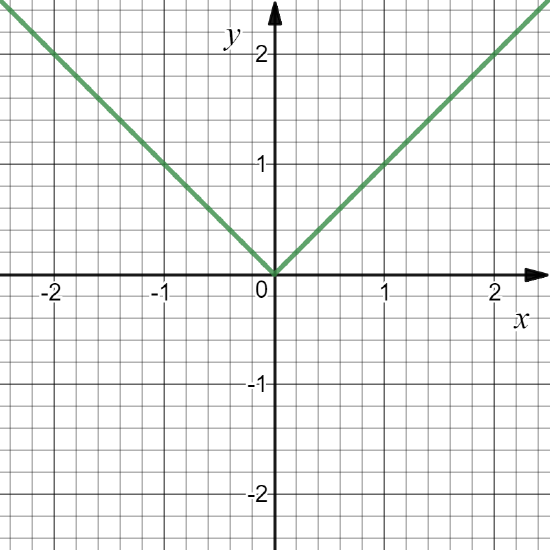
Example \PageIndex{16}
Define f: \mathbb{R}\to \mathbb{R} by f(x)=|x|.
Note that \sqrt{x^2}=|x|.
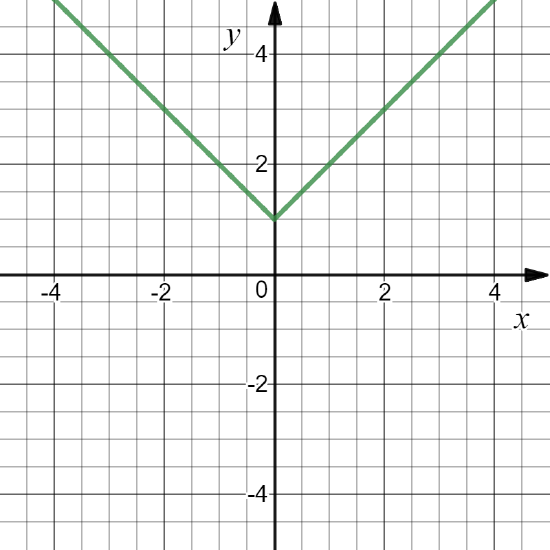
Exercise \PageIndex{17}
Define f: \mathbb{R}\to \mathbb{R} by f(x)=|x|+1
- Answer
-
Step functions
Example \PageIndex{18}: Sign function
Define f: \mathbb{R\setminus\{0\}}\to \mathbb{R} by f(x)=\frac{|x|}{x}.
Example \PageIndex{19}: Unit Step function
Define f: \mathbb{R}\to \mathbb{R} by f(x)=.
Key Concepts
- A function is a mapping from a set of inputs to a set of outputs with exactly one output for each input.
- If no domain is stated for a function y=f(x),
- the domain is considered to be the set of all real numbers x
- for which the function is defined.
- When sketching the graph of a function f,
- each vertical line may intersect the graph, at most, once.
- A function may have any number of zeros, but it has, at most, one y-intercept.
- To define the composition g∘f, the range of f must be contained in the domain of g.
- Even functions are symmetric about the y-axis whereas odd functions are symmetric about the origin.
- The power function f(x)=x^n is an even function if n is even and n≠0, and it is an odd function if n is odd.
- The root function f(x)=x^{1/n} has the domain [0,∞) if n is even and the domain (−∞,∞) if n is odd. If n is odd, then f(x)=x^{1/n} is an odd function.
- The domain of the rational function f(x)=p(x)/q(x), where p(x) and q(x) are polynomial functions, is the set of x such that q(x)≠0.
- Functions that involve the basic operations of addition, subtraction, multiplication, division, and powers are algebraic functions. All other functions are transcendental. Trigonometric, exponential, and logarithmic functions are examples of transcendental functions.
- A polynomial function f with degree n≥1 satisfies f(x)→±∞ as x→±∞. The sign of the output as x→∞ depends on the sign of the leading coefficient only and on whether n is even or odd.
- Vertical and horizontal shifts, vertical and horizontal scalings, and reflections about the x- and y-axes are examples of transformations of functions.
Key Equations
- Point-slope equation of a line y−y1=m(x−x_1)\nonumber
- Slope-intercept form of a line y=mx+b\nonumber
- Standard form of a line ax+by=c\nonumber
- Polynomial function f(x)=a_n^{x^n}+a_{n−1}x^{n−1}+⋯+a_1x+a_0\nonumber
- Composition of two functions
g∘f)(x)=g(f(x))
- Absolute value function
f(x)=\begin{cases}−x&x<0\\x&x≥0\end{cases}
Glossary
- absolute value function
- f(x)=\begin{cases}−x&x<0\\x&x≥0\end{cases}
- composite function
- given two functions f and g, a new function, denoted g∘f, such that (g∘f)(x)=g(f(x))
- decreasing on the interval II
- a function decreasing on the interval I if, for all x_1,x_2∈I,f(x_1)≥f(x_2) if x_1<x_2
- dependent variable
- the output variable for a function
- domain
- the set of inputs for a function
- even function
- a function is even if f(−x)=f(x) for all x in the domain of f
- function
- a set of inputs, a set of outputs, and a rule for mapping each input to exactly one output
- graph of a function
- the set of points (x,y) such that x is in the domain of f and y=f(x)
- increasing on the interval II
- a function increasing on the interval I if for all x1,x2∈I,f(x1)≤f(x2) if x1<x2
- independent variable
- the input variable for a function
- odd function
- a function is odd if f(−x)=−f(x) for all x in the domain of f
- range
- the set of outputs for a function
- symmetry about the origin
- the graph of a function f is symmetric about the origin if (−x,−y) is on the graph of f whenever (x,y) is on the graph
- symmetry about the y-axis
- the graph of a function f is symmetric about the y-axis if (−x,y) is on the graph of f whenever (x,y) is on the graph
- table of values
- a table containing a list of inputs and their corresponding outputs
- vertical line test
- given the graph of a function, every vertical line intersects the graph, at most, once
- zeros of a function
- when a real number x is a zero of a function f,f(x)=0
- algebraic function
- a function involving any combination of only the basic operations of addition, subtraction, multiplication, division, powers, and roots applied to an input variable x
- cubic function
- a polynomial of degree 3; that is, a function of the form f(x)=ax^3+bx^2+cx+d, where a≠0
- degree
- for a polynomial function, the value of the largest exponent of any term
- linear function
- a function that can be written in the form f(x)=mx+b
- logarithmic function
- a function of the form f(x)=log_b(x) for some base b>0,b≠1 such that y=log_b(x) if and only if b^y=x
- mathematical model
- A method of simulating real-life situations with mathematical equations
- piecewise-defined function
- a function that is defined differently on different parts of its domain
- point-slope equation
- equation of a linear function indicating its slope and a point on the graph of the function
- polynomial function
- a function of the form f(x)=a_nx^n+a_{n−1}x^{n−1}+…+a_1x+a_0
- power function
- a function of the form f(x)=x^n for any positive integer n≥1
- quadratic function
- a polynomial of degree 2; that is, a function of the form f(x)=ax^2+bx+c where a≠0
- rational function
- a function of the form f(x)=p(x)/q(x), where p(x) and q(x) are polynomials
- root function
- a function of the form f(x)=x^{1/n} for any integer n≥2
- slope
- the change in y for each unit change in x
- slope-intercept form
- equation of a linear function indicating its slope and y-intercept
- transcendental function
- a function that cannot be expressed by a combination of basic arithmetic operations
- transformation of a function
- a shift, scaling, or reflection of a function
Contributors and Attributions
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.
Pamini Thangarajah (Mount Royal University, Calgary, Alberta, Canada)

