4.6E: Exercises
This page is a draft and is under active development.
( \newcommand{\kernel}{\mathrm{null}\,}\)
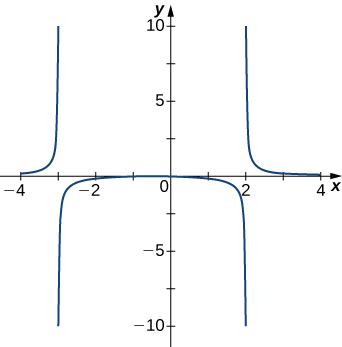
3)
- Answer
- x=−1,x=2
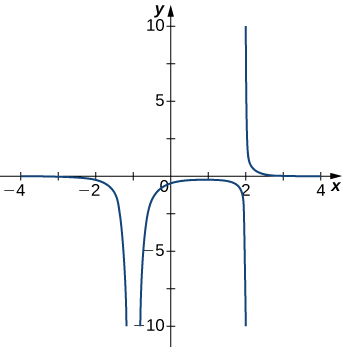
4)
5)
- Answer
- x=0
For the functions f(x) in exercises 6 - 10, determine whether there is an asymptote at x=a. Justify your answer without graphing on a calculator.
6) f(x)=x+1x2+5x+4,a=−1
7) f(x)=xx−2,a=2
- Answer
- Yes, there is a vertical asymptote at x=2.
8) f(x)=(x+2)3/2,a=−2
9) f(x)=(x−1)−1/3,a=1
- Answer
- Yes, there is vertical asymptote at x=1.
10) f(x)=1+x−2/5,a=1
In exercises 11 - 20, evaluate the limit.
11) limx→∞13x+6
- Answer
- limx→∞13x+6=0
12) limx→∞2x−54x
13) limx→∞x2−2x+5x+2
- Answer
- limx→∞x2−2x+5x+2=∞
14) limx→−∞3x3−2xx2+2x+8
15) limx→−∞x4−4x3+12−2x2−7x4
- Answer
- limx→−∞x4−4x3+12−2x2−7x4=−17
16) limx→∞3x√x2+1
17) limx→−∞√4x2−1x+2
- Answer
- limx→−∞√4x2−1x+2=−2
18) limx→∞4x√x2−1
19) limx→−∞4x√x2−1
- Answer
- limx→−∞4x√x2−1=−4
20) limx→∞2√xx−√x+1
For exercises 21 - 34, find the horizontal and vertical asymptotes.
21) f(x)=x−9x
- Answer
- Horizontal: none,
Vertical: x=0
22) f(x)=11−x2
23) f(x)=x34−x2
- Answer
- Horizontal: none,
Vertical: x=±2
24) f(x)=x2+3x2+1
25) f(x)=sin(x)sin(2x)
- Answer
- Horizontal: none,
Vertical: none
- Solution
-
Since f(x) is a continuous function, it doesn't have horizontal or vertical asymptotes.
26) f(x)=cosx+cos(3x)+cos(5x)
27) f(x)=xsin(x)x2−1
- Answer
- Horizontal: y=0,
Vertical: x=±1
- Solution
-
We know that −1≤sin(x)≤1. Which implies −xx2−1≤xsin(x)x2−1≤xx2−1. Since limx→∞xx2−1=0 and limx→∞xx2−1=0, by Squeeze theorem, limx→∞xsin(x)x2−1=0. Hence f(x) has an horizontal asymptote y=0. Since limx→1+xsin(x)x2−1=∞ and limx→1−xsin(x)x2−1=−∞, x=1 is a vertical symptote. Since limx→−1+xsin(x)x2−1=∞ and limx→−1−xsin(x)x2−1=−∞, x=−1 is a vertical symptote.
28) f(x)=xsin(x)
29) f(x)=1x3+x2
- Answer
- Horizontal: y=0,
Vertical: x=0 and x=−1
- Solution
-
limx→∞1x3+x2=0. Hence f(x) has an horizontal asymptote y=0. Since f(x)=1x3+x2=1x2(x+1), x=0 and x=−1 are possible vertical asymptotes.
limx→0+1x2(x+1)=∞ and limx→0−1x2(x+1)=∞, x=0 is a vertical symptote. Since limx→−1+1x2(x+1)=∞ and \displaystyle\lim_{x\to -1^-} \dfrac{1}{x^2(x+1)}}=-\infty, x=−1 is a vertical symptote.
30) f(x)=1x−1−2x
31) f(x)=x3+1x3−1
- Answer
- Horizontal: y=1,
Vertical: x=1
- Solution
-
limx→∞x3+1x3−1=1. Hence f(x) has an horizontal asymptote y=1. Since f(x)=x3+1x3−1=x3+1(x−1)(x2+x+1), x=1 is a possible vertical asymptote. Since limx→1+1x2(x+1)=∞ and \displaystyle\lim_{x\to 1^-} \dfrac{1}{x^2(x+1)}}=-\infty, x=1 is a vertical symptote.
32) f(x)=sinx+cosxsinx−cosx
33) f(x)=x−sinx
- Answer
- Horizontal: none,
Vertical: none
- Solution
-
Since f(x) is a continuous function, it doesn't have horizontal or vertical asymptotes.
34) f(x)=1x−√x
For exercises 35 - 38, construct a function f(x) that has the given asymptotes.
35) x=1 and y=2
- Answer
- Answers will vary, for example: y=2xx−1
36) x=1 and y=0
37) y=4,x=−1
- Answer
- Answers will vary, for example: y=4xx+1
38) x=0
In exercises 39 - 43, graph the function on a graphing calculator on the window x=[−5,5] and estimate the horizontal asymptote or limit. Then, calculate the actual horizontal asymptote or limit.
39) [T] f(x)=1x+10
- Answer
- limx→∞1x+10=0 so f has a horizontal asymptote of y=0.
40) [T] f(x)=x+1x2+7x+6
41) [T] limx→−∞x2+10x+25
- Answer
- limx→−∞x2+10x+25=∞
42) [T] limx→−∞x+2x2+7x+6
43) [T] limx→∞3x+2x+5
- Answer
- limx→∞3x+2x+5=3 so this function has a horizontal asymptote of y=3.
In exercises 44 - 55, draw a graph of the functions without using a calculator. Be sure to notice all important features of the graph: local maxima and minima, inflection points, and asymptotic behavior.
44) y=3x2+2x+4
45) y=x3−3x2+4
- Answer
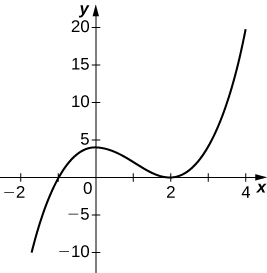
46) y=2x+1x2+6x+5
47) y=x3+4x2+3x3x+9
- Answer
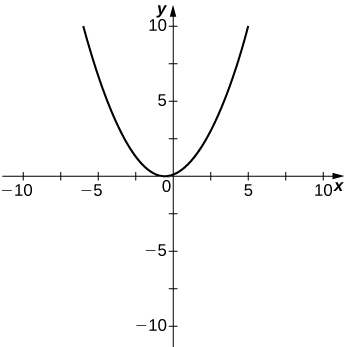
48) y=x2+x−2x2−3x−4
49) y=√x2−5x+4
- Answer
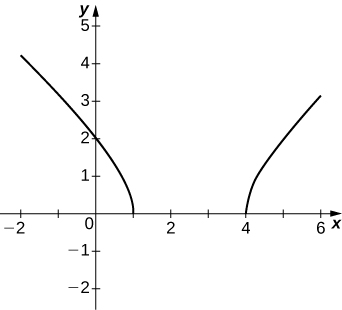
50) y=2x√16−x2
51) y=cosxx, on x=[−2π,2π]
- Answer
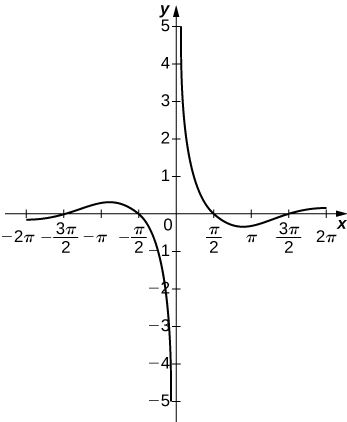
52) y=e^x−x^3
53) y=x\tan x, \quad x=[−π,π]
- Answer
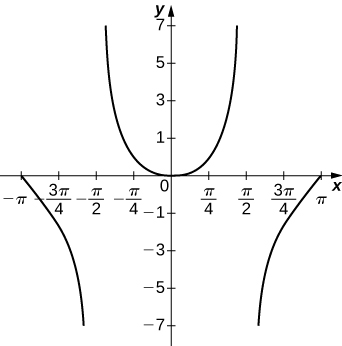
54) y=x\ln(x), \quad x>0
55) y=x^2\sin(x),\quad x=[−2π,2π]
- Answer
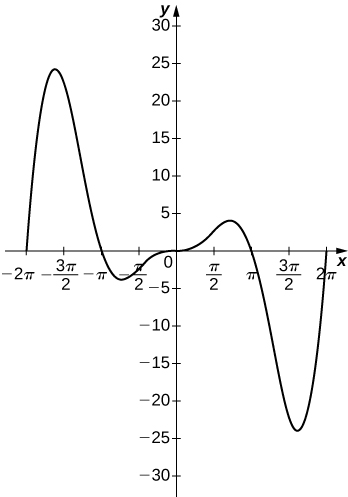
56) For f(x)=\dfrac{P(x)}{Q(x)} to have an asymptote at y=2 then the polynomials P(x) and Q(x) must have what relation?
57) For f(x)=\dfrac{P(x)}{Q(x)} to have an asymptote at x=0, then the polynomials P(x) and Q(x). must have what relation?
- Answer
- Q(x). must have have x^{k+1} as a factor, where P(x) has x^k as a factor.
58) If f′(x) has asymptotes at y=3 and x=1, then f(x) has what asymptotes?
59) Both f(x)=\dfrac{1}{x−1} and g(x)=\dfrac{1}{(x−1)^2} have asymptotes at x=1 and y=0. What is the most obvious difference between these two functions?
- Answer
- \displaystyle \lim_{x→1^−}f(x)=-\infty \text{ and } \lim_{x→1^−}g(x)=\infty
60) True or false: Every ratio of polynomials has vertical asymptotes.
Exercise \PageIndex{8}: Limit at infinity
1. Find \displaystyle \lim_{x \to \infty} \sqrt{x^2+3}-x
- Answer
-
To find \displaystyle \lim_{x \to \infty} \sqrt{x^2+3}-x, First multiply by the conjugate
\displaystyle \lim_{x \to \infty} \sqrt{x^2+3}-x = \lim_{x \to \infty} \frac{(\sqrt{x^2+3}-x)(\sqrt{x^2+3}+x)}{\sqrt{x^2+3}+x}
Then reduce the numerator
\displaystyle \lim_{x \to \infty} \sqrt{x^2+3}-x = \lim_{x \to \infty} \frac{3}{\sqrt{x^2+3}+x}
Now divide by \sqrt{x^2}=|x|,
\displaystyle \lim_{x \to \infty} \sqrt{x^2+3}-x = \lim_{x \to \infty} \frac{3/|x|}{(\sqrt{x^2+3}+x)/ \sqrt{x^2}}
Since x \to \infty, replace |x| by x.
Thus, \( \displaystyle \lim_{x \to \infty} \sqrt{x^2+3}-x = \lim_{x \to \infty} \frac{3/x}{(\sqrt{1+3/\sqrt{x^2}}+x/x\)
This result will be:
\displaystyle = 3(0)/ 2
\displaystyle = 0
2. Find \displaystyle \lim_{x \to - \infty} \frac{\sqrt{x^4+6x}}{x^2-6}
- Answer
-
Factor out the highest degree variable in the numerator and the denominator, \displaystyle \sqrt{x^4}=|x^2|=x^2.
\displaystyle \lim_{x \to - \infty} \frac{\sqrt{x^4+6x}}{x^2-6} = \lim_\limits{x \to - \infty} \frac{x^2\sqrt{1 + \frac{6x}{x^3}}}{(x^2)(1- \frac{6}{x^2})}
Evaluate:
\displaystyle = \frac{\sqrt{1+0}}{1-0}
\displaystyle = \frac{1}{1}
\displaystyle = 1
3. Find \displaystyle \lim\limits_{t \to \infty} \frac{7-t}{\sqrt{2+2t^2}}
- Answer
-
Factor out the highest degree variable in the numerator and denominator
= \displaystyle \lim\limits_{t \to\infty} \frac{t (\frac{7}{t} -1)}{|t|\sqrt{\frac{2}{t^2}+2}}
Evaluate:
\displaystyle = \frac{0-1}{\sqrt{0+2}}
\displaystyle = \frac{-1}{\sqrt{2}}
4.Find \displaystyle \lim_{t \to - \infty} \frac{7-t}{\sqrt{2+2t^2}}
- Answer
-
Factor out the highest degree variable in the numerator and denominator
\displaystyle =\lim_{t \to \infty} \frac{(t)(\frac{7}{t}-1)}{|t|\sqrt{\frac{2}{t^2}+2}}
\displaystyle = \frac{0-1}{(-1)\sqrt{0+2}}
\displaystyle = \frac{1}{\sqrt{2}}
5.Find \displaystyle \lim_{y \to - \infty} \frac{\sqrt{4y^2-2}}{2-y}
- Answer
-
Factor out the highest degree variable in the numerator and denominator
\displaystyle = \lim_{y \to -\infty} \frac{y\sqrt{4-\frac{2}{y^2}}}{|y|(\frac{2}{y}-1)}
When y \to -\infty |y | approaches to -\infty.
Evaluate:
\displaystyle \frac{\sqrt{4-0}}{-(0-1)}
\displaystyle \frac{2}{1}
\displaystyle 2
6.Find \displaystyle \lim_{s \to \infty} \sqrt[5]{ \frac{5s^8 - 4s^3}{2s^8-1}}
- Answer
-
Because the limit is approaching infinity, only the highest degree polynomials need to be considered. This then simplifies the limit to:
= \displaystyle \lim_{s \to \infty} \sqrt[5]{\frac{5s^8}{2s^8}}
= \displaystyle \sqrt[5]{\frac{5}{2}}
7.Find \displaystyle \lim_{x \to \infty} \sqrt[3]{ \frac{3+2x+5x^2}{1+4x^2}}
- Answer
-
Because the limit is approaching infinity, only the highest degree polynomials need to be considered. This then simplifies the limit to:
\displaystyle = \lim_{x \to \infty} \sqrt[3]{\frac{5x^2}{4x^2}}
\displaystyle = \sqrt[3]{\frac{5}{4}}.
8.Find \displaystyle \lim_{t \to \infty} \frac {11-t^5}{11t^5 +1}
- Answer
-
Because the limit is approaching infinity, only the highest degree polynomials need to be considered. This then simplifies the limit to:
\displaystyle = \lim_{t \to \infty} \frac {-t^5}{11t^5}
\displaystyle = \frac {-1}{11}
9.Find \displaystyle \lim_{x \to -\infty} \frac{3}{x-3}
- Answer
-
\displaystyle = 0
10.Find \displaystyle \lim_{x \to \infty} \frac{3x^2-2x}{5x^2+1}
- Answer
-
Because the limit is approaching infinity, only the highest degree polynomials need to be considered. This then simplifies the limit to:
\displaystyle = \lim_{x \to -\infty} \frac{3x^2}{5x^2}
\displaystyle = \frac{3}{5}.
11.Find \displaystyle\lim_{y \to -\infty} \frac{\sqrt{7y^2+6y-8}}{5-y}.
- Answer
-
\displaystyle\lim_{y \to -\infty} \frac{\sqrt{7y^2+6y-8}}{5-y}= \displaystyle\lim_{y \to -\infty} \frac{\sqrt{7y^2}}{-y}
\displaystyle\lim_{y \to -\infty} \frac{\frac{\sqrt{7y^2}}{|y|}}{\frac{-y}{|y|}}= \displaystyle\lim_{y \to -\infty} \frac{\frac{\sqrt{7y^2}}{\sqrt{y^2}}}{\frac{-y}{-y}} = \sqrt{7}
Exercise \PageIndex{9}: Horizontal Asymptotes
Find horizontal asymptote(s) of the function
1. y= \displaystyle \frac{5+3x}{ \sqrt{x^2+x-4}}.
2. y=f(x)= x- \sqrt{x^2+2x-6}.
3.f(x)=\dfrac{x^2-5x+6}{x^2-4x+3}}
Justify your work using limits.
- Answer
-
1. y=3 and y=-3.
Contributors and Attributions
Gregory Hartman (Virginia Military Institute). Contributions were made by Troy Siemers and Dimplekumar Chalishajar of VMI and Brian Heinold of Mount Saint Mary's University. This content is copyrighted by a Creative Commons Attribution - Noncommercial (BY-NC) License. http://www.apexcalculus.com/
Pamini Thangarajah (Mount Royal University, Calgary, Alberta, Canada)
Exercises 8 and 9 are by Pamini Thangarajah.

