4.1: Greatest Common Factor and Factor by Grouping
- Page ID
- 66316
By the end of this section, you will be able to:
- Find the greatest common factor of two or more polynomials
- Factor the greatest common factor from a polynomial
- Factor by grouping
Before you get started, take this readiness quiz.
- Factor \(56\) into primes.
- Find the least common multiple (LCM) of \(18\) and \(24\).
- Multiply \(−3a(7a+8b)\).
Find the Greatest Common Factor of a Polynomial
Earlier we multiplied factors together to get a product. Now, we will reverse this process; we will start with a product and then break it down into its factors. Splitting a product into factors is called factoring.
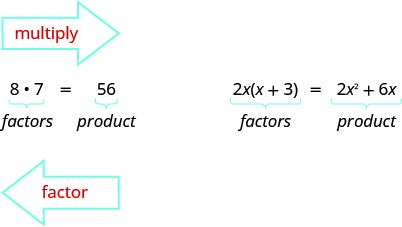
Above, we have recalled how to factor numbers to find the least common multiple (LCM) of two or more numbers. Our goal is to be able to factor polynomials. The first step is to find the greatest common factor of a given polynomial. The method we use is similar to what we can use to find the LCM.
- If we write a polynomial \(P\) as a product of polynomials, we say that we have factored \(P\).
- A polynomial \(F\) is a factor of \(P\) if we can write \(P\) as \(P=F\cdot G\) for some polynomial \(G\).
- The greatest common factor (GCF) of two or more monomials is a monomial \(F\) that satisfies the following conditions:
- \(F\) is a factor of all the monomials, that is, \(F\) is a common factor, and
- any other common factor of all the monomials is a factor of \(F\).
- The greatest common factor (GCF) of a polynomial is the GCF of its terms.
While we say the greatest common factor, there are actually two: one with a positive coefficient and one with a negative coefficient.
We use “factor” as both a noun and a verb:
\[\begin{array} {ll} \text{Noun:} &\hspace{30mm} 7 \text{ is a factor of }14 \\ \text{Verb:} &\hspace{30mm} \text{factor }3 \text{ from }3a+3\end{array}\nonumber\]
We summarize the steps we use to find the greatest common factor.
- Factor each coefficient into primes. Write all variables with exponents in expanded form.
- List all factors—matching common factors in a column. In each column, circle the common factors.
- Bring down the common factors that all polynomials share.
- Multiply the factors.
The next example will show us the steps to find the greatest common factor of three monomials.
Find the greatest common factor of \(21x^3\), \(9x^2\), and \(15x\).
- Solution
-
\(21x^3\), \( 9x^2\), \(15x\) Factor each coefficient into primes and write the
variables with exponents in expanded form.
Circle the common factors in each column.
Bring down the common factors.\(\begin{align*}21x^3 &= {\color{red}{3}}\cdot \quad \quad 7\cdot {\color{red}{x}}\cdot x\cdot x\\9x^2 &= {\color{red}{3}}\cdot 3\cdot \quad\quad {\color{red}{x}}\cdot x \\ 15x &= {\color{red}{3}}\cdot \quad 5 \cdot \quad {\color{red}{x}}\\ \text{GCF}&={\color{red}{3}}\cdot \quad \quad \quad {\color{red}{x}}\end{align*}\)
Multiply the factors. \(\text{GCF }=3x\) Answer the question. The GCF of \(21x^3\), \(9x^2\), and \(15x\) is \(3x\).
Find the greatest common factor of \(25m^4\), \(35m^3\), and \(20m^2.\)
- Answer
-
The GCF is \(5m^2\).
Find the greatest common factor of \(14x^3\), \(70x^2\), and \(105x\).
- Answer
-
The GCF is \(7x\).
Factor the Greatest Common Factor from a Polynomial
It is sometimes useful to represent a number as a product of factors, for example, \(12\) as \(2\cdot 6\) or \(3\cdot 4\). In algebra, it can also be useful to represent a polynomial in factored form. We will start with a product, such as \(3x^2+15x\), and end with a product of its factors, \(3x(x+5)\). To do this we apply the Distributive Property “in reverse.”
We state the Distributive Property here just as you saw it in earlier chapters and “in reverse.”
If \(a\), \(b\), and \(c\) are real numbers, then
\[a(b+c)=ab+ac\nonumber\]
and
\[ab+ac=a(b+c).\nonumber\]
The form on the left is used to multiply. The form on the right is used to factor.
So how do you use the Distributive Property to (partially) factor a polynomial? You just find the GCF of all the terms and write the polynomial as a product!
Factor \(8m^3−12m^2n+20mn^2\).
- Solution
-
\(8m^3−12m^2n+20mn^2\) Find the GCF of all the termsof the polynomial. Find the GCF of \(8m^3\), \(12m^2n\), and \(20mn^2\). 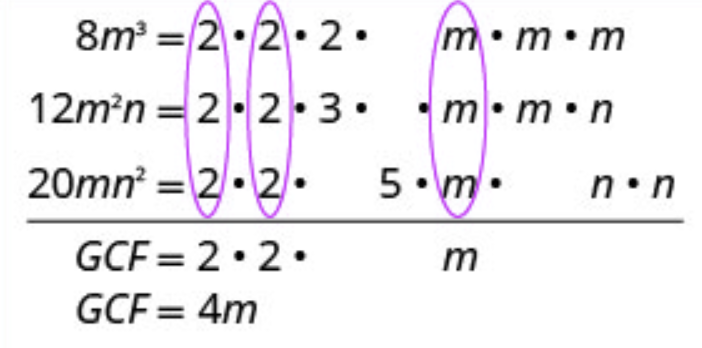
Rewrite each term as a product using the GCF. Rewrite \(8m^3\), \(12m^2n\), and \(20mn^2\) as products of their GCF, \(4m\). \(\quad 8m^3−12m^2n+20mn^2\)
\(= {\color{red}4m\cdot} 2m^2 - {\color{red}4m\cdot} 3mn +{\color{red} 4m\cdot} 5n^2\)
Use the "reverse" Distributive Property to factor the expression. \(={\color{red} 4m}(2m^2-3mn+5n^2)\) Check by multiplying the factors. \(\quad 4m(2m^2-3mn+5n^2)\)
\(= 4m\cdot 2m^2-4m\cdot 3mn+4m\cdot 5n^2\)
\(= 8m^3-12m^2n+20n^2\quad\checkmark\)
Factor \(9xy^2+6x^2y^2+21y^3\).
- Answer
-
\(3y^2(3x+2x^2+7y)\)
Factor \(3p^3−6p^2q+9pq^3\).
- Answer
-
\(3p(p^2−2pq+3q^3)\)
- Find the GCF of all the terms of the polynomial.
- Rewrite each term as a product using the GCF.
- Use the “reverse” Distributive Property to factor the polynomial.
- Check by multiplying the factors.
Factor out the GCF of \(5x^3−25x^2\).
- Solution
-
\(5x^3−25x^2\) Find the GCF of \(5x^3\) and \(25x^2\). 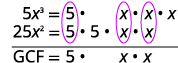
The GCF is \(5x^2\).
Rewrite each term. \(\quad 5x^3−25x^2\)
\(={\color{red}{5x^2}}\cdot x-{\color{red}{5x^2}}\cdot 5\)
Factor the GCF. \(=5x^2(x-5)\) Check.
\(\quad 5x^2(x−5) \)
\(=5x^2\cdot x−5x^2\cdot 5 \)
\(=5x^3−25x^2 \quad\checkmark\)
Factor out the GCF of \(2x^3+12x^2\).
- Answer
-
\(2x^2(x+6)\)
Factor out the GCF of \(6y^3−15y^2\).
- Answer
-
\(3y^2(2y−5)\)
Factor out the GCF of \(8x^3y−10x^2y^2+12xy^3\).
- Solution
-
\(8x^3y−10x^2y^2+12xy^3\) The GCF of \(8x^3y,\space −10x^2y^2,\) and \(12xy^3\)
is \(2xy\).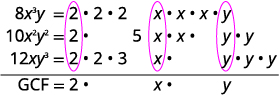
The GCF is \(2xy\).
Rewrite each term using the GCF, \(2xy\). \(\quad 8x^3y−10x^2y^2+12xy^3\)
\(={\color{red}{2xy}}\cdot 4x^2-{\color{red}{2xy}}\cdot 5xy + {\color{red}{2xy}}\cdot 6y^2\)
Factor the GCF. \(=2xy(4x^2−5xy+6y^2)\) Check.
\(\quad 2xy(4x^2−5xy+6y^2)\)
\(=2xy\cdot 4x^2−2xy\cdot 5xy+2xy\cdot 6y^2\)
\(=8x^3y−10x^2y^2+12xy^3\quad\checkmark\)
Factor out the GCF of \(15x^3y−3x^2y^2+6xy^3\).
- Answer
-
\(3xy(5x^2−xy+2y^2)\)
Factor out the GCF of \(8a^3b+2a^2b^2−6ab^3\).
- Answer
-
\(2ab(4a^2+ab−3b^2)\)
When the leading coefficient is negative, we factor the negative out as part of the GCF.
Factor out the GCF of \(−4a^3+36a^2−8a\).
- Solution
-
The leading coefficient is negative, so the GCF will be negative.
\(\quad −4a^3+36a^2−8a\) Rewrite each term using the GCF, \(−4a\). \(={\color{red}{-4a}}\cdot a^2 {\color{red}{-4a}}\cdot(-9a) {\color{red}{-4a}}\cdot 2\) Factor the GCF. \(=−4a(a^2−9a+2)\) Check.
\(\quad −4a(a^2−9a+2)\)
\(=−4a\cdot a^2−(−4a)\cdot 9a+(−4a)\cdot 2\)
\(=−4a^3+36a^2−8a\quad\checkmark\)
Factor out the GCF of \(−4b^3+16b^2−8b\).
- Answer
-
\(−4b(b^2−4b+2)\)
Factor out the GCF of \(−7a^3+21a^2−14a\).
- Answer
-
\(−7a(a^2−3a+2)\)
In the next example, we extend the idea of factoring out the GCF to a binomial.
Factor out the common factor of the two terms of \(3y(y+7)−4(y+7)\).
- Solution
-
\(\quad 3y(y+7)−4(y+7)\) The binomial \(y+7\) is a common factor of the two terms.
\(=3y{\color{red}{(y+7)}}−4{\color{red}{(y+7)}}\) Factor \((y+7)\). \(=(y+7)(3y-4)\) Check. \(\quad 3y(y+7)−4(y+7)\)
\(=3y\cdot y + 3y \cdot 7 -4y-4\cdot 7\)
\(=3y^2+21y-4y-28\)
\(=3y^2+17y -28\)
\(\quad (y+7)(3y-4)\)
\(=y\cdot 3y +y(-4)+7\cdot 3y +7\cdot (-4)\)
\(=3y^2-4y+21y-28\)
\(=3y^2+17y-28\quad\checkmark\)
Factor out the common factor of the two terms of \(4m(m+3)−7(m+3)\).
- Answer
-
\((m+3)(4m−7)\)
Factor out the common factor of the two terms of \(8n(n−4)+5(n−4)\).
- Answer
-
\((n−4)(8n+5)\)
Factor by Grouping
Sometimes there is no common factor of all the terms of a polynomial. When there are four terms we separate the polynomial into two parts with two terms in each part. Then look for the GCF in each part. If the polynomial can be factored, you will find a common factor emerges from both parts. Not all polynomials can be factored.
Factor by grouping: \(xy+3y+2x+6\).
- Solution
-
\(xy+3y+2x+6\) Group terms with common factors. Is there a greatest common factor of all four terms?
No, so let's separate the first two terms from the second two.
\(\quad xy+3y+2x+6\)
\(=\underbrace{xy+3y}{}+\underbrace{2x+6}{}\)
Factor out the common factor in each group. Factor the GCF from the first two terms.
Factor the GCF from the second two terms.
\(=y(x+3)+\underbrace{2x+6}{}\)
\(=y(x+3)+2(x+3)\)
Factor the common factor from the expression. Notice that each terms has a common factor of \(x+3\). \(=y{\color{red}{(x+3)}}+2{\color{red}{(x+3)}}\)
\(=(x+3)(y+2)\)
Check. Multiply \((x+3)(y+2)\). Is the product the original expression? \(\quad (x+3)(y+2)\)
\(=xy+2x+3y+6\)
\(=xy+3y+2x+6\quad \checkmark\)
Factor by grouping: \(xy+8y+3x+24\).
- Answer
-
\((x+8)(y+3)\)
Factor by grouping: \(ab+7b+8a+56\).
- Answer
-
\((a+7)(b+8)\)
- Group terms with common factors.
- Factor out the common factor in each group.
- Factor the common factor from the polynomial.
- Check by multiplying the factors.
Factor by grouping:
a. \(x^2+3x−2x−6\)
b. \(6x^2−3x−4x+2\)
- Solution
-
a.
\(\quad x^2+3x−2x−6\) There is no GCF in all four terms. \(=x^2+3x−2x−6\) Separate into two parts. \(=\underbrace{x^2+3x}{}\underbrace{−2x−6}{}\) Factor the GCF from both parts. Be careful with the signs when factoring the GCF from the last two terms. \(=x(x+3)−2(x+3)\) Factor out the common factor, \(x+3\). \(=(x+3)(x−2)\) Check. \(\quad (x+3)(x−2)\)
\(=x^2-2x+3x-6\)
\(=x^2+x-6\)
b.\(\quad 6x^2−3x−4x+2\) There is no GCF in all four terms. \(=6x^2−3x−4x+2\) Separate into two parts. \(=\underbrace{6x^2−3x}{}\underbrace{−4x+2}{}\) Factor the GCF from both parts. Be careful with the signs when factoring the GCF from the last two terms. \(=3x(2x−1)−2(2x−1)\) Factor out the common factor, \(2x-1\). \(=(2x−1)(3x−2)\) Check. \(\quad (2x−1)(3x−2)\)
\(=6x^2-4x-3x+2\)
\(=6x^2-3x-4x+2\)
Factor by grouping:
a. \(x^2+2x−5x−10\)
b. \(20x^2−16x−15x+12\)
- Answer
-
a. \((x−5)(x+2)\)
b. \((5x−4)(4x−3)\)
Factor by grouping:
a. \(y^2+4y−7y−28\)
b. \(42m^2−18m−35m+15\)
- Answer
-
a. \((y+4)(y−7)\)
b. \((7m−3)(6m−5)\)
Key Concepts
- Factor as a Noun and a Verb: We use “factor” as both a noun and a verb.
\[\begin{array} {ll} \text{Noun:} &\quad 7 \text{ is a factor of } 14\\ \text{Verb:} &\quad \text{factor }3 \text{ from }3a+3\end{array}\nonumber\]
- How to find the greatest common factor (GCF) of two polynomials.
- Factor each coefficient into primes. Write all variables with exponents in expanded form.
- List all factors—matching common factors in a column. In each column, circle the common factors.
- Bring down the common factors that all polynomials share.
- Multiply the factors.
- Distributive Property: If \(a\), \(b\) and \(c\) are real numbers, then
\[a(b+c)=ab+ac\quad \text{and}\quad ab+ac=a(b+c)\nonumber\]
The form on the left is used to multiply. The form on the right is used to factor. - How to factor the greatest common factor from a polynomial.
- Find the GCF of all the terms of the polynomial.
- Rewrite each term as a product using the GCF.
- Use the “reverse” Distributive Property to factor the polynomial.
- Check by multiplying the factors.
- How to factor by grouping.
- Group terms with common factors.
- Factor out the common factor in each group.
- Factor the common factor from the polnomial.
- Check by multiplying the factors.
Glossary
- factoring a polynomial
- Writing a polynomial as a product is called factoring.
- greatest common factor
- The greatest common factor (GCF) of two or more polynomials is the largest polynomial that is a factor of all the expressions.
Practice Makes Perfect
Find the Greatest Common Factor of Two or More Expressions
In the following exercises, find the greatest common factor.
1. \(10p^3q,12pq^2\)
- Answer
-
\(2pq\)
2. \(8a^2b^3,10ab^2\)
3. \(12m^2n^3,30m^5n^3\)
- Answer
-
\(6m^2n^3\)
4. \(28x^2y^4,42x^4y^4\)
5. \(10a^3,12a^2,14a\)
- Answer
-
\(2a\)
6. \(20y^3,28y^2,40y\)
7. \(35x^3y^2,10x^4y,5x^5y^3\)
- Answer
-
\(5x^3y\)
8. \(27p^2q^3,45p^3q^4,9p^4q^3\)
Factor the Greatest Common Factor from a Polynomial
In the following exercises, factor the greatest common factor from each polynomial.
9. \(6m+9\)
- Answer
-
\(3(2m+3)\)
10. \(14p+35\)
11. \(9n−63\)
- Answer
-
\(9(n−7)\)
12. \(45b−18\)
13. \(3x^2+6x−9\)
- Answer
-
\(3(x^2+2x−3)\)
14. \(4y^2+8y−4\)
15. \(8p^2+4p+2\)
- Answer
-
\(2(4p^2+2p+1)\)
16. \(10q^2+14q+20\)
17. \(8y^3+16y^2\)
- Answer
-
\(8y^2(y+2)\)
18. \(12x^3−10x\)
19. \(5x^3−15x^2+20x\)
- Answer
-
\(5x(x^2−3x+4)\)
20. \(8m^2−40m+16\)
21. \(24x^3−12x^2+15x\)
- Answer
-
\(3x(8x^2−4x+5)\)
22. \(24y^3−18y^2−30y\)
23. \(12xy^2+18x^2y^2−30y^3\)
- Answer
-
\(6y^2(2x+3x^2−5y)\)
24. \(21pq^2+35p^2q^2−28q^3\)
25. \(20x^3y−4x^2y^2+12xy^3\)
- Answer
-
\(4xy(5x^2−xy+3y^2)\)
26. \(24a^3b+6a^2b^2−18ab^3\)
27. \(−2x−4\)
- Answer
-
\(−2(x+4)\)
28. \(−3b+12\)
29. \(−2x^3+18x^2−8x\)
- Answer
-
\(−2x(x^2−9x+4)\)
30. \(−5y^3+35y^2−15y\)
31. \(−4p^3q−12p^2q^2+16pq^2\)
- Answer
-
\(−4pq(p^2+3pq−4q)\)
32. \(−6a^3b−12a^2b^2+18ab^2\)
33. \(5x(x+1)+3(x+1)\)
- Answer
-
\((x+1)(5x+3)\)
34. \(2x(x−1)+9(x−1)\)
35. \(3b(b−2)−13(b−2)\)
- Answer
-
\((b−2)(3b−13)\)
36. \(6m(m−5)−7(m−5)\)
Factor by Grouping
In the following exercises, factor by grouping.
37. \(ab+5a+3b+15\)
- Answer
-
\((b+5)(a+3)\)
38. \(cd+6c+4d+24\)
39. \(8y^2+y+40y+5\)
- Answer
-
\((y+5)(8y+1)\)
40. \(6y^2+7y+24y+28\)
41. \(uv−9u+2v−18uv\)
- Answer
-
\((u+2)(v−9)\)
42. \(pq−10p+8q−80\)
43. \(u^2−u+6u−6\)
- Answer
-
\((u−1)(u+6)\)
44. \(x^2−x+4x−4\)
45. \(9p^2−15p+12p−20\)
- Answer
-
\((3p−5)(3p+4)\)
46. \(16q^2+20q−28q−35\)
47. \(mn−6m−4n+24\)
- Answer
-
\((n−6)(m−4)\)
48. \(r^2−3r−r+3\)
49. \(2x^2−14x−5x+35\)
- Answer
-
\((x−7)(2x−5)\)
50. \(4x^2−36x−3x+27\)
Mixed Practice
In the following exercises, factor.
51. \(−18xy^2−27x^2y\)
- Answer
-
\(−9xy(3x+2y)\)
52. \(−4x^3y^5−x^2y^3+12xy^4\)
53. \(3x^3−7x^2+6x−14\)
- Answer
-
\((x^2+2)(3x−7)\)
54. \(x^3+x^2−x−1\)
55. \(x^2+xy+5x+5y\)
- Answer
-
\((x+y)(x+5)\)
56. \(5x^3−3x^2+5x−3\)
Writing Exercises
57. What does it mean to say a polynomial is in factored form?
- Answer
-
Answers will vary.
58. How do you check result after factoring a polynomial?
59. The greatest common factor of \(36\) and \(60\) is \(12\). Explain what this means.
- Answer
-
Answers will vary.
60. What is the GCF of \(y^4,\space y^5\), and \(y^{10}\)? Write a general rule that tells you how to find the GCF of \(y^a,\space y^b\), and \(y^c\).
Self Check
a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
b. If most of your checks were:
…confidently. Congratulations! You have achieved your goals in this section! Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific!
…with some help. This must be addressed quickly as topics you do not master become potholes in your road to success. Math is sequential - every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Who can you ask for help? Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?
…no - I don’t get it! This is critical and you must not ignore it. You need to get help immediately or you will quickly be overwhelmed. See your instructor as soon as possible to discuss your situation. Together you can come up with a plan to get you the help you need.
F

