1.6: Applications
- Page ID
- 223
A Dictionary for Variation Problems
| Term | Math |
| Varies Directly as | = k times |
| Varies Inversely as | = k/ |
| Is Proportional to | = k times |
| Is Inversely Proportional to | = k/ |
Applications Involving Variation
Example \(\PageIndex{1}\)
Einstein proposed that the energy produced by annihilating matter is directly proportional to the mass of the atom. Suppose that a nuclear fission reaction resulted in a loss of .01 kg of matter. The resulting energy produced was 9X1014 N.
- Write the equation that expresses this phenomena.
- Find the constant of proportionality.
- If one electron is annihilated then \(8.2\times 10^{14}\) units of energy are released. Calculate the mass of an electron.
Example \(\PageIndex{2}\)
Suppose that the number of customers you have in your hardware store is proportional to the square root of the money spent on advertising. Last month, you spent $2,000 on advertising and had 800 customers. If you want 1,000 customers, how much should you spend on advertising?
Example \(\PageIndex{3}\)
You want to build a 20 foot tall rectangular house and put expensive wood on all sides except the back. You have 2,500 square feet of expensive wood.
- Express the area of the house as a function of the length of the back.
- State the domain.
- Generate the graph and find the largest possible area.
Example \(\PageIndex{4}\)
The intensity of sound varies inversely as the cube of the distance from the source. Find an equation that relates the intensity and the distance. By what factor will the intensity decrease as the distance from the source moves from 2 meters to 4 meters?
Example \(\PageIndex{5}\)
A train leaves Carson City traveling 40 miles per hour heading North towards Reno which is 50 miles away. When the train leaves you are 60 miles due east of Carson City.
- Express the trains distance from you starting place as a function of time. What are the domain and range of this function?
- If you head towards Reno at the same time as the train and arrive in Reno at the same time as the train, express the distance from your location to the train's location as a function of time. What are the domain and range?
Example \(\PageIndex{6}\)
The electric resistance R of a wire varies directly as its length L and inversely as the square of its radius r.
- What happens to the resistance if the length and radius are both tripled?
- How must the length be changed if the resistance and the radius are both to be doubled?
Example \(\PageIndex{7}\)
The ideal gas law states that the pressure of a contained gas is proportional to the temperature and inversely proportional to the volume of the container. If at 273 degrees Kelvin, 2 cubic meters of a gas has a pressure of 2 atmospheres,
- If the container is unchanged, but the temperature is increased to 280 degrees, what will be the pressure of the gas?
- If the has is allowed to expand into a 3 cubic meter container and the temperature remains constant, what will the resulting pressure be?
Example \(\PageIndex{8}\)
A church window has the shape of a rectangle surmounted by a semicircle.
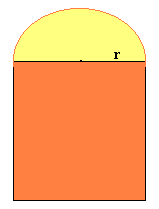
- Express the area \(A\) of the window as a function of the radius \(r\) of the semicircle if the perimeter of the window is 30 feet.
- Use a graphing calculator to generate the graph of the function defined in part \(A\). Trace to the peak of the curve, then state the value of \(r\) that makes the area of the window the largest possible.
- Use the value of \(r\) from part \(b\) to estimate the length y when the area of the window is the largest possible. Make a conjecture about the values of \(r\) and \(y\) when the area of the window is the largest possible.
Contributors
- Larry Green (Lake Tahoe Community College)
Integrated by Justin Marshall.


