6.2: New Variables
- Page ID
- 8343
In order to understand the solution in all mathematical details we make a change of variables
\[w = x + ct,\quad z = x - ct . \nonumber \]
We write \(u(x,t)=\bar u(w,z)\). We find
\[\begin{align} \dfrac{\partial}{\partial x} u & = \dfrac{\partial}{\partial w}{\bar u}\dfrac{\partial}{\partial x} w + \dfrac{\partial}{\partial z} {\bar u}\dfrac{\partial}{\partial x} z = \dfrac{\partial}{\partial w}{\bar u} + \dfrac{\partial}{\partial z} {\bar u}, \nonumber\\[4pt] \dfrac{\partial^2}{\partial x^2} u & = \dfrac{\partial^2}{\partial w^2}{\bar u}+2 \dfrac{\partial^2}{\partial w \partial z} {\bar u}+ \dfrac{\partial}{\partial z} {\bar u}, \nonumber\\[4pt] \dfrac{\partial}{\partial t} u & = \dfrac{\partial}{\partial w}{\bar u}\dfrac{\partial}{\partial t} w + \dfrac{\partial}{\partial z} {\bar u}\dfrac{\partial}{\partial t} z = c\left(\dfrac{\partial}{\partial w}{\bar u} - \dfrac{\partial}{\partial z} {\bar u}\right), \nonumber\\[4pt] \dfrac{\partial^2}{\partial t^2} u & = c^2\left(\dfrac{\partial^2}{\partial w^2}{\bar u}-2 \dfrac{\partial^2}{\partial w \partial z} {\bar u}+ \dfrac{\partial}{\partial z} {\bar u} \right)\end{align} \nonumber \]
We thus conclude that
\[\dfrac{\partial^2}{\partial x^2} u(x,t) - \frac{1}{c^2} \dfrac{\partial^2}{\partial t^2} u(x,t) = 4\dfrac{\partial^2}{\partial w \partial z} {\bar u} = 0 \nonumber \]
An equation of the type \(\dfrac{\partial^2}{\partial w \partial z} {\bar u} = 0\) can easily be solved by subsequent integration with respect to \(z\) and \(w\). First solve for the \(z\) dependence,
\[\dfrac{\partial}{\partial w}{\bar u} = \Phi(w), \label{eq5} \]
where \(\Phi\) is any function of \(w\) only. Now solve this equation for the \(w\) dependence, \[\bar u(w,z) = \int \Phi(w) dw = F(w) + G(z) \nonumber \] In other words, with \(F\) and \(G\) arbitrary functions.
6.2.1: Infinite String
Equation \ref{eq5} is quite useful in practical applications. Let us first look at how to use this when we have an infinite system (no limits on \(x\)). Assume that we are treating a problem with initial conditions
\[u(x,0) = f(x),\;\;\dfrac{\partial}{\partial t} u(x,0) = g(x). \nonumber \]
Let me assume \(f(\pm\infty)=0\). I shall assume this also holds for \(F\) and \(G\) (we don’t have to, but this removes some arbitrary constants that don’t play a rôle in \(u\)). We find
\[\begin{align} F(x)+G(x) &= f(x),\nonumber\\[4pt] c(F'(x)-G'(x)) & = g(x).\end{align} \nonumber \]
The last equation can be massaged a bit to give
\[F(x)-G(x) = \underbrace{\frac{1}{c}\int_0^x g(y) dy}_{=\Gamma(x)} + C \nonumber \]
Note that \(\Gamma\) is the integral over \(g\). So \(\Gamma\) will always be a continuous function, even if \(g\) is not!
And in the end we have
\[\begin{align} F(x) &= \dfrac{1}{2} \left[f(x) +\Gamma(x)+C\right]\nonumber\\[4pt] G(x) &= \dfrac{1}{2} \left[f(x) -\Gamma(x)-C\right] \end{align} \nonumber \]
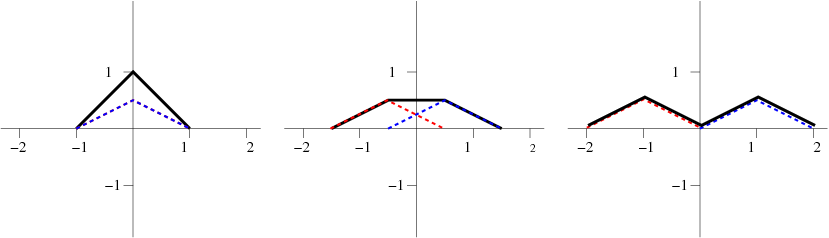
Suppose we choose (for simplicity we take \(c=1 \text{m/s}\))
\[f(x) = \begin{cases} x+1 & \text{if $-1<x<0$} \\ 1-x & \text{if $0<x<1$} \\ 0 & \text{elsewhere} \end{cases} . \nonumber \]
and \(g(x)=0\). The solution is then simply given by \[u(x,t) = \dfrac{1}{2} \left[f(x+t)+f(x-t)\right]. \label{eq.11} \] This can easily be solved graphically, as shown in Figure \(\PageIndex{1}\).
6.2.2: Finite String
The case of a finite string is more complex. There we encounter the problem that even though \(f\) and \(g\) are only known for \(0<x<a\), \(x\pm ct\) can take any value from \(-\infty\) to \(\infty\). So we have to figure out a way to continue the function beyond the length of the string. The way to do that depends on the kind of boundary conditions: Here we shall only consider a string fixed at its ends.
\[\begin{align} u(0,t) &=u(a,t)=0,\nonumber\\[4pt] u(x,0)&=f(x)\\[4pt] \dfrac{\partial}{\partial t} u (x,0) &= g(x).\end{align} \nonumber \]
Initially we can follow the approach for the infinite string as sketched above, and we find that
\[\begin{align} F(x) &= \dfrac{1}{2} \left[f(x) +\Gamma(x)+C\right], \nonumber\\[4pt] G(x) &= \dfrac{1}{2} \left[f(x) -\Gamma(x)-C\right]. \end{align} \nonumber \]
Look at the boundary condition \(u(0,t)=0\). It shows that
\[\dfrac{1}{2} [f(ct)+f(-ct)]+\dfrac{1}{2} [\Gamma(ct)-\Gamma(-ct)]=0. \nonumber \]
Now we understand that \(f\) and \(\Gamma\) are completely arbitrary functions – we can pick any form for the initial conditions we want. Thus the relation found above can only hold when both terms are zero
\[\begin{align} f(x)&=-f(-x),\nonumber\\[4pt] \Gamma(x)&=\Gamma(x).\label{eq:refl1}\end{align} \]
Now apply the other boundary condition, and find
\[\begin{align} f(a+x)&=-f(a-x),\nonumber\\[4pt] \Gamma(a+x)&=\Gamma(a-x).\label{eq:refl2}\end{align} \]
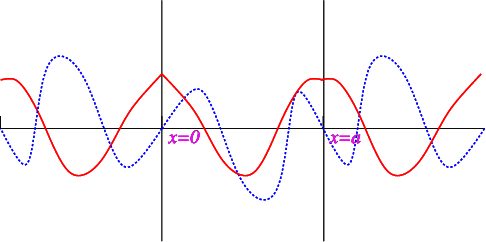
The reflection conditions for \(f\) and \(\Gamma\) are similar to those for sines and cosines, and as we can see from Figure \(\PageIndex{2}\) both \(f\) and \(\Gamma\) have period \(2a\).


