10.3: Closeness Centrality
( \newcommand{\kernel}{\mathrm{null}\,}\)
Degree centrality measures might be criticized because they only take into account the immediate ties that an actor has, or the ties of the actor's neighbors, rather than indirect ties to all others. One actor might be tied to a large number of others, but those others might be rather disconnected from the network as a whole. In a case like this, the actor could be quite central, but only in a local neighborhood.
Closeness centrality approaches emphasize the distance of an actor to all others in the network by focusing on the distance from each actor to all others. Depending on how one wants to think of what it means to be "close" to others, a number of slightly different measures can be defined.
Path Distances
Network>Centrality>Closeness provides a number of alternative ways of calculating the "far-ness" of each actor from all others. Far-ness is the sum of the distance (by various approaches) from each ego to all others in the network.
"Far-ness" is then transformed into "nearness" as the reciprocal of far-ness. That is, nearness = one divided by far-ness. "Nearness" can be further standardized by norming against the minimum possible nearness for a graph of the same size and connection.
Given a measure of nearness or far-ness for each actor, we can again calculate a measure of inequality in the distribution of distances across the actors, and express "graph centralization" relative to that of the idealized "star" network.
Figure 10.9 shows a dialog for calculating closeness measures of centrality and graph centralization.
Figure 10.9: Dialog for Network>Centrality>Closeness
Several alternative approaches to measuring "far-ness" are available in the type setting. The most common is probably the geodesic path distance. Here, "far-ness" is the sum of the lengths of the shortest paths from ego (or to ego) from all other nodes. Alternatively, the reciprocal of this, or "nearness" can be calculated. Alternatively, one may focus on all paths, not just geodesics or all trails. Figure 10.10 shows the results for the Freeman geodesic path approach.
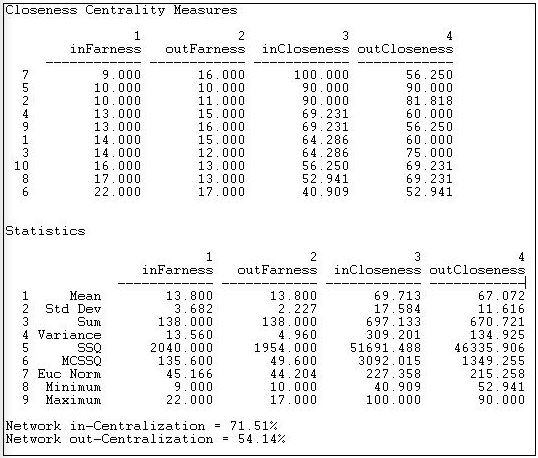
Figure 10.10: Geodesic path closeness centrality for Knoke information network
Since the information network is directed, separate closeness and far-ness can be computed for sending and receiving. We see that actor 6 has the largest sum of geodesic distances from other actors (in-far-ness of 22) and to other actors (out-far-ness of 17). The far-ness figures can be re-expressed as nearness (the reciprocal of far-ness) and normed relative to the greatest nearness observed in the graph (here, the in-closeness of actor 7).
Summary statistics on the distribution of the nearness and far-ness measures are also calculated. We see that the distribution of out-closeness has less variability than in-closeness, for example. This is also reflected in the graph in-centralization
Reach
Another way of thinking about how close an actor is to all others is to ask what portion of all others ego can reach in one step, two steps, three steps, etc. The routine Network>Centrality>Reach Centrality calculates some useful measures of how close each actor is to all others. Figure 10.11 shows the results for the Knoke information network.
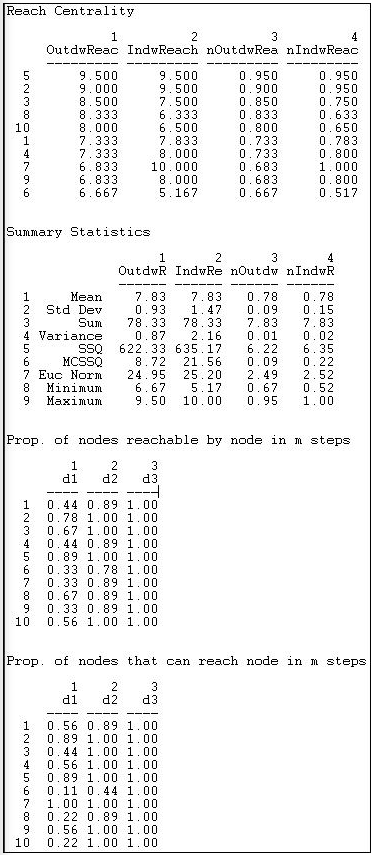
Figure 10.11: Reach centrality for Knoke information network
An index of the "reach distance" from each ego to (or from) all others is calculated. Here, the maximum score (equal to the number of nodes) is achieved when every other is one step from ego. The reach closeness sum becomes less as actors are two steps, three steps, and so on (weights of 1/2, 1/3, etc.). These scores are then expressed in "normed" form by dividing by the largest observed reach value.
The final two tables are quite easy to interpret. The first of these shows what proportion of other nodes can be reached from each actor at one, two, and three steps (in our example, all others are reachable in three steps or less). The last table shows what proportions of others can reach ego at one, two, and three steps. Note that everyone can contact the newspaper (actor 7) in one step.
Eigenvector of Geodesic Distance
The closeness centrality measure described above is based on the sum of the geodesic distances from each actor to all others (far-ness). In larger and more complex networks than the example we've been considering, it is possible to be somewhat misled by this measure. Consider two actors, A and B. Actor A is quite close to a small and fairly closed group within a larger network, and rather distant from many of the members of the population. Actor B is at a moderate distance from all of the members of the population. The far-ness measures for actor A and actor B could be quite similar to magnitude. In a sense, however, actor B is really more "central" than actor A in this example, because B is able to reach more of the network with the same amount of effort.
The eigenvector approach is an effort to find the most central actors (i.e. those with the smallest far-ness from others) in terms of the "global" or "overall" structure of the network, and to pay less attention to patterns that are more "local". The method used to do this (factor analysis) is beyond the scope of the current text. In a general way, what factor analysis does is to identify "dimensions" of the distances among actors. The location of each actor with respect to each dimension is called an "eigenvalue", and the collection of such values is called the "eigenvector". Usually, the first dimension captures the "global" aspects of distances among actors; second and further dimensions capture more specific and local substructures.
The UCINET Network>Centrality>Eigenvector routine calculates individual actor centrality, and graph centralization using weights on the first eigenvector. A limitation of the routine is that it does not calculate values for asymmetric data. So, our measures here are based on the notion of "any connection".
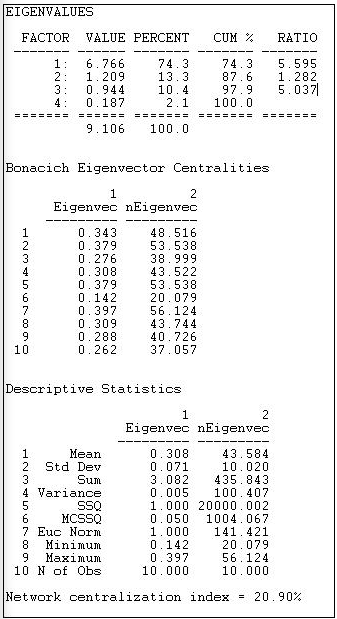
Figure 10.12: Eigenvector centrality and centralization for Knoke information network
The first set of statistics, the eigenvalues, tell us how much of the overall pattern of distances among actors can be seen as reflecting the global pattern (the first eigenvalue), and more local, or additional patterns. We are interested in the percentage of the overall variation in distances that is accounted for by the first factor. Here, this percentage is
Next, we turn our attention to the scores of each of the cases on the 1
Last, we examine the overall centralization of the graph, and the distribution of centralities. There is relatively little variability in centralities (standard deviation 0.07) around the mean (0.31). This suggests that, overall, there are not great inequalities in actor centrality or power, when measured in this way. Compared to the pure "star" network, the degree of inequality or concentration of the Knoke data is only
Geodesic distances among actors are a reasonable measure of one aspect of centrality - or positional advantage. Sometimes these advantages may be more local, and sometimes more global. The factor-analytic approach is one approach that may sometimes help us to focus on the more global pattern. Again, it is not that one approach is "right" and the other "wrong". Depending on the goals of our analysis, we may wish to emphasize one or the other aspects of the positional advantages that arise from centrality.
Hubbell, Katz, Taylor, Stephenson, and Zelen Influence Measures
The geodesic closeness and eigenvalue approaches consider the closeness of connection to all other actors, but only by the "most efficient" path (the geodesic). In some cases, power or influence may be expressed through all of the pathways that connect an actor to all others. Several measures of closeness based on all connections of ego to others are available from Network>Centrality>Influence.
Even if we want to include all connections between two actors, it may not make a great deal of sense to consider a path of length 10 as important as a path of length 1. The Hubbell and Katz approaches count the total connections between actors (ties for undirected data, both sending and receiving ties for directed data). Each connection, however, is given a weight according to its length. The greater the length, the weaker the connection. How much weaker the connection becomes with increasing length depends on an "attenuation" factor. In our example, below, we have used an attenuation factor of 0.5. That is, an adjacency receives a weight of one, a walk of length two receives a weight of 0.5, a connection of length three receives a weight of 0.5 squared (0.25), etc. The Hubbell and Katz approaches are very similar. Katz includes an identity matrix (a connection of each actor with itself) as the strongest connection; the Hubbell approach does not. As calculated by UCINET, both approaches "norm" the results to range from largest negative distances (that is, the actors are very close relative to the other pairs, or have high cohesion) to large positive numbers (that is, the actors have large distance relative to others). The results of the Hubbell and Katz approaches are shown in Figures 10.13 and 10.14.
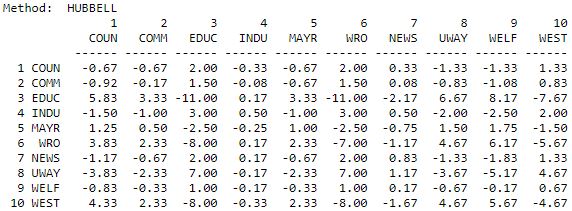
Figure 10.13: Hubbell dyadic influence for the Knoke information network
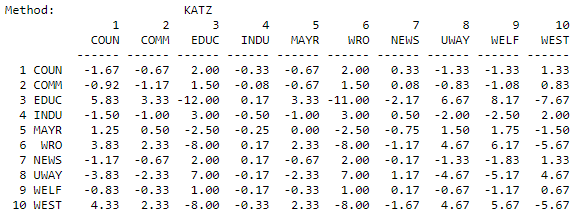
Figure 10.14: Katz dyadic influence for the Knoke information network
As with all measures of pair-wise properties, one could analyze the data much further. We could see which individuals are similar to which others (that is, are there different groups or strata defined by the similarity of their total connections to all others in the network?). Our interest might also focus on the whole network, where we might examine the degree of variance, and the shape of the distribution of the dyads' connections. For example, a network in which the total connections among all pairs of actors might be expected to behave very differently than one where there are radical differences among actors.
The Hubbell and Katz approach may make the most sense when applied to symmetric data, because they pay no attention to the directions of connections (i.e. A's ties directed to B are just as important as B's ties to A in defining the distance or solidarity - closeness - between them). If we are more specifically interested in the influence of A on B in a directed graph, the Taylor influence approach provides an interesting alternative.
The Taylor measure, like the others, uses all connections, and applies an attenuation factor. Rather than standardizing on the whole resulting matrix, however, a different approach is adopted. The column marginals for each actor are subtracted from the row marginals, and the result is then normed (what did he say?!). Translated into English, we look at the balance between each actor sending connections (row marginals) and their receiving connections (column marginals). Positive values then reflect a preponderance of sending over receiving to the other actor of the pair - or a balance of influence between the two. Note that the newspaper (#7) shows as being a net influencer with respect to most other actors in the result below, while the welfare rights organization (#6) has a negative balance of influence with most other actors. The results for the Knoke information network are shown in Figure 10.15.
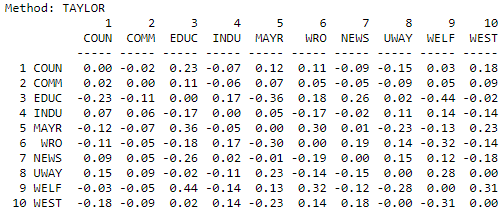
Figure 10.15: Taylor dyadic influence for the Knoke information network
Yet another measure based on attenuating and norming all pathways between each actor and all others was proposed by Stephenson and Zelen, and can be computed with Network>Centrality>Information. This measure, shown in Figure 10.16, provides a more complex norming of the distances from each actor to each other, and summarizes the centrality of each actor with the harmonic mean of its distance to the others.
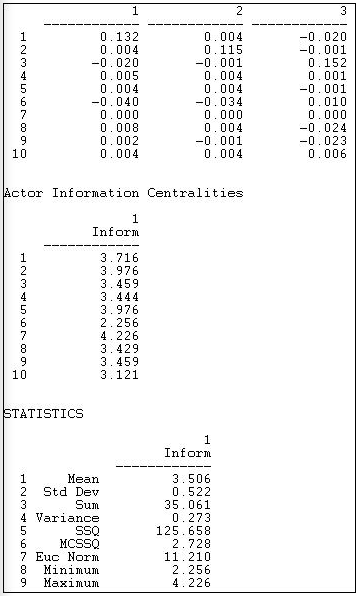
Figure 10.16: Stephenson and Zelen information centrality of Knoke information network
The (truncated) top panel shows the dyadic distance of each actor to each other. The summary measure is shown in the middle panel, and information about the distribution of the centrality scores is shown in the statistics section.
As with most other measures, the various approaches to the distance between actors and in the network as a whole provide a menu of choices. No one definition to measuring distance will be the "right" choice for a given purpose. Sometimes we don't really know, beforehand, what approach might be best, and we may have to try and test several.


