4.5: Highlighting parts of the network
- Page ID
- 7669
Large networks (those that contain many actors, many kinds of relations, and/or high densities of ties) can be very difficult to visualize in any useful way -- there is simply too much information. Often, we need to clear away some of the "clutter" to see main patterns more clearly.
One of the most interesting features of social networks -- whether small or large -- is the extent to which we can locate "local sub-structures." We will discuss this topic a good bit more in a later chapter. Highlighting or focusing attention on sub-sets of nodes in a drawing can be a powerful tool for visualizing sub-structures.
In this section, we will briefly outline some approaches to rendering network drawings that can help to simplify complex diagrams and locate interesting sub-graphs (i.e. collections of nodes and their connections).
Clearing away the underbrush
Social structures can be composed of multiple relations. Bob, Carol, Ted, and Alice in our earlier example are a multi-plex structure of people connected by both friendship and by spousal ties. Graphs that display all of the connections among a set of nodes can be very useful for understanding how actors are tied together -- but they can also get so complicated and dense that it is difficult to see any patterns. There are a couple approaches that can help.
One approach is to combine multiple relations into an index. For example, one could combine the information on friendship and spousal ties using an "and" rule: if two nodes have both a friendship and spousal tie, then they have a tie - otherwise they do not (i.e. if they have no tie, or only one type of tie). Alternatively, we could create an index that records a tie when there is either a friendship tie or a spousal tie. If we had measured relations with values, rather than simple presence-absence, multiple relations could be combined by addition, subtraction, multiplication, division, averaging, or other methods. UCINET has tools for these kinds of operations, that are located at: Transform>matrix operations>within dataset>aggregations.
The other approach is to simplify the data a bit. NetDraw has some tools that can be of some help.
Rather than examining the information on multiple kinds of ties in one diagram, one can look at them one at a time, or in combination. If the data have been stored as a UCINET or NetDraw data file with multiple relations, then the Options>View>Relations Box opens a dialog box that lets you select which relations you want to display. Suppose that we had a data set in which we had recorded the friendship ties among a number of people at intervals over a period of time. By first displaying the first time point, and then adding subsequent time point, we can visualize the evolution of the friendship structure.
It isn't unusual for some of the nodes in a graph of a social network to not be connected to the others at all. Nodes that aren't connected are called "isolates." Some nodes may be connected to the network by a single tie. These nodes sort of "dangle" from the diagram; they are called "pendants." One way of simplifying graphs is to hide isolates and/or pendants to reduce visual clutter. Of course, this does mis-represent the structure, but it may allow us to focus more attention where most of the action is. NetDraw has both button-bar tools and a menu item (Analysis>Isolates) to hide these less-connected nodes.
Finding and visualizing local sub-structures
One of the common questions in network analysis is whether a graph displays various kinds of "sub-structures." For example, a "clique" is a sub-structure that is defined as a set of nodes where every element of the set is connected to every other member. A network that has no cliques might be a very different place than a network that has many small cliques, or one that has one clique and many nodes that are not part of the clique. We'll take a closer look at UCINET tools for identifying sub-structures in a later chapter.
NetDraw has built-in a number of tools for identifying sub-structures, and automatically coloring the graph to identify them visually.
Analysis>components locates the parts of graph that are completely disconnected from one another, and colors each set of nodes (i.e. each component). In our Bob-Carol-Ted-Alice example, the entire graph is one component, because all the actors are connected. In the welfare bureaucracies example, there are two components, one composed of only WRO (which does not receive ties from any other organization) and the other composed of the other nine nodes. In NetDraw, executing this command also creates a variable in the database of node attributes -- as do all the other commands discussed here. These attributes can then be used for selecting cases, changing color, shape, and size, etc.
Analysis>Blocks and Cutpoints locates parts of the graph that would become disconnected components if either one node or one relation were removed (the blocks are the resulting components; the cutpoint is the node that would, if removed, create the dis-connect). NetDraw graphs these sub-structures, and saves the information in the node-attribute database.
Analysis>K-cores locates parts of the graph that form sub-groups such that each member of a sub-group is connected to N-K of the other members. That is, groups are the largest structures in which all members are connected to all but some number (K) of other members. A "clique" is a group like this where all members are connected to all other members; "fuzzier" or "looser" groups are created by increasing "K." NetDraw identifies the K-cores that are created by different levels of K, and provides colored graphs and data-base entries.
Analysis>Subgroups>block based. Sorry, but I don't know what this algorithm does! Most likely, it creates sub-structures that would become components with differing amounts of nodes/relations removed.
Analysis>Subgroups>Hierarchical Clustering of Geodesic Distances. The geodesic distance between two nodes is the length of the shortest path between them. A hierarchical clustering of distances produces a tree-like diagram in which the two nodes that are most similar in their profile of distances to all other points are joined into a cluster; the process is then repeated over and over until all nodes are joined. The resulting graphic is one way of understanding which nodes are most similar to one another, and how the nodes may be classified into "types" based on their patterns of connection to other nodes. The graph is colored to represent the clusters, and database information is stored about the cluster memberships at various levels of aggregation. A hierarchical clustering can be very interesting in understanding which groups are more homogeneous (those that group together at early stages in the clustering) than others; moving up the clustering tree diagram, we can see a sort of a "contour map" of the similarity of nodes.
Analysis>Subgroups>Factions (select number). A "faction" is a part of a graph in which the nodes are more tightly connected to one another than they are to members of other "factions." This is quite an intuitively appealing idea of local clustering or sub-structure (though, as you can see, only one such idea). NetDraw asks you how many factions you would like to find (always explore various reasonable possibilities!). The algorithm then forms the number of groups that you desire by seeking to maximize connection within, and minimize connection between the groups. Points are colored, and the information about which nodes fall in which partitions (i.e. which cases are in which factions) is saved to the node attributes database.
Analysis>Subgroups>Newman-Girvan. This is another numerical algorithm that seeks to create clusters of nodes that are closely connected within, and less connected between clusters. The approach is that of "block modeling." Rows and columns are moved to try to create "blocks" where all connections within a block are present, and all connections between blocks are absent. This algorithm will usually produce results similar to the factions algorithm. Importantly, though, the Newman-Girvan algorithm also produces measures of goodness-of-fit of the configuration for two blocks, three blocks, etc. This allows you to get some sense of what division into blocks is optimal for your needs (there isn't one "right" answer).
Ego Networks (neighborhoods)
A very useful way of understanding complicated network graphs is to see how they arise from the local connections of individual actors. The network formed by selecting a node, including all actors that are connected to that node, and all the connections among those other actors is called the "ego network" or (1-step) neighborhood of an actor. Figure 4.9 is an example from the Knoke bureaucracies information network, where we select as our "ego" the board of education.
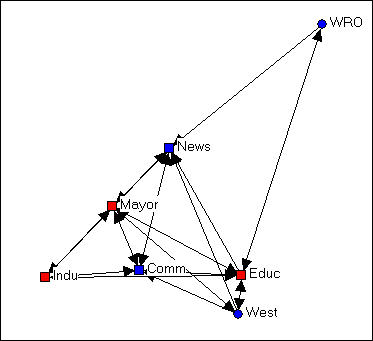
Figure 4.9. Ego network of Educ in Knoke information network
We note that the ego-network of the board of education is fairly extensive, and that the density of connection among the actors in the ego-network is fairly high. This is to say say the the board of education is quite "embedded" in a dense local sub-structure.
Next, let's add the ego network of the "West" agency, in figure 4.10.

Figure 4.10. Ego networks of Educ and West in Knoke information network
The two ego networks combined result in a fully connected structure. We note that one connection between Educ and Coun is mediated by West.
One can often gain considerable insight about complicated networks by "building" them starting with one actor and adding others. Or, one can begin with the whole network, and see what happens as individual's ego networks are removed.
The network of each individual actor may also be of considerable interest. Who's most connected? How dense are the neighborhoods of particular actors?
NetDraw has useful tools for visualizing and working with ego-networks. The Layout>Egonet command presents a dialog box that lets you select which ego's networks are to be displayed. You can start with all the actors and delete; or start with focal actors and build up the full network.


