4.4: Location, location, location
( \newcommand{\kernel}{\mathrm{null}\,}\)
Most graphs of networks are drawn in a two-dimensional "X-Y axis" space (Mage and some other packages allow 3-dimensional rendering and rotation). Where a node or a relation is drawn in the space is essentially arbitrary -- the full information about the network is contained in its list of nodes and relations. The figures below are exactly the same network (Knoke's money flow network) that has been rendered in several different ways.
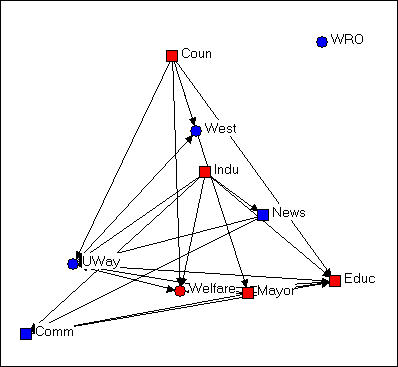
Figure 4.4. Random configuration of Knoke's money network
This drawing was created using NetDraw's Layout>Random on the graph that we had previously "colored" (blue for non-government, red for government; circles for welfare specialists, squares for generalists). This algorithm locates the nodes randomly in the X-Y space (you can use other tools to change the size of the graphic, rotate it, etc.). Since the X and Y directions don't "mean" anything, the location of the nodes and relations don't provide any particular insight.
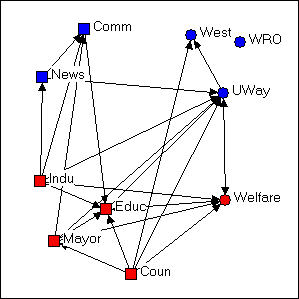
Figure 4.5. Free-hand grouping by attributes configuration of Knoke's money network
In Figure 4.5, we've used the "drag and drop" method ("grab" a node with the cursor, and drag it to a new location) to relocate the nodes so that organizations that share the same combinations of attributes are located in different quadrants of the graph. Since we had hypothesized that organizations of like "kind" would have higher rates of connection, this is a useful (but still arbitrary) way to locate the points. If the hypothesis were strongly supported (and its not) most of the arrows would be located within each the four quadrants, and there would be few arrows between quadrants. NetDraw has a built-in tool that allows the user to assign the X and Y dimensions of the graph to scores on attributes (either categorical or continuous): Layout>Attributes as Coordinates, and then select attributes to be assigned to X or Y or both. This can be a very useful tool for exploring how patterns of ties differ within and between "partitions" (or types of nodes).
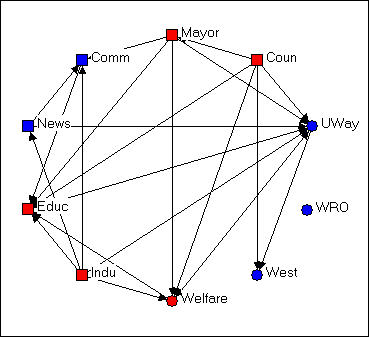
Figure 4.6. Circle configuration of Knoke's money network
Figure 4.6 shows the same graph using Layout>Circle, and selecting the "generalist-specialist" (i.e. the circle or square node type) as the organizing criterion. Circle graphs are commonly used to visualize which nodes are most highly connected. The nodes are located at equal distances around a circle, and nodes that are highly connected are very easy to quickly locate (e.g. UWay, Educ) because of the density of lines. When nodes sharing the same attribute are located together in a segment of the circle, the density of ties within and between types is also quite apparent.
In each of the different layouts we've discussed so far, the distances between the nodes are arbitrary, and can't be interpreted in any meaningful way as "closeness" of the actors. And, the "directions" X and Y have no meaning -- we could rotate any of the graphs any amount, and it would not change a thing about our interpretation. There are several other commonly used graphic layouts that do try to make the distances and/or directions of locations among the actors somewhat more meaningful.

Figure 4.7. Non-metric multi-dimensional scaling configuration of Knoke's money network
Figure 4.7 was generated using the Layout>Graph Theoretic Layout>MDS tool of NetDraw. MDS stands for (non-metric, in this case) "Multi-Dimensional Scaling." MDS is a family of techniques that is used (in network analysis) to assign locations to nodes in multi-dimensional space (in the case of the drawing, a 2-dimensional space) such that nodes that are "more similar" are closer together. There are many reasonable definitions of what it means for two nodes to be "similar." In this example, two nodes are "similar" to the extent that they have similar shortest paths (geodesic distances) to all other nodes. There are many, many ways of doing MDS, but the default tools chosen in NetDraw can often generate meaningful renderings of graphs that provide insights. NetDraw has several built-in algorithms for generating coordinates based on similarity (metric and non-metric two-dimensional scaling, and principle components analysis).
One very important difference between figure 4.7 and the earlier graphs is that the distances between the nodes is interpretable. The "Welfare" and "Mayor" nodes are very similar in their geodesic distances from other actors. "West" and "Educ" have very different patterns of ties to the other nodes.
The other important difference between figure 4.7 and the earlier graphs is that direction may be meaningful. Notice that there is a cluster of nodes at the left (News, Indu, Comm) that are all pretty much not welfare organizations themselves, while the nodes at the right are (generally) more directly involved in welfare service provision. The upper left-hand quadrant contains mostly "blue" nodes, while the lower right quadrant contains mostly "red" ones -- so one "direction" might be interpreted as "non-government/government."
Let me emphasize that different applications of MDS (and other scaling tools) to different definitions of what it means for nodes to be "similar" can generate wildly different looking graphs. These are (almost always) exploratory techniques, and there is (usually) no single "correct" interpretation. But, a graphic that uses both distance and direction to summarize something about the structure of the network can provide considerable insight when compared to graphs (like figures 4.4, 4.5, and 4.6) that don't.
Consider one last example of rendering the same data, this time using NetDraw's unique built-in algorithm for locating points (Layout>Graph Theoretic Layout>Spring Embedding).
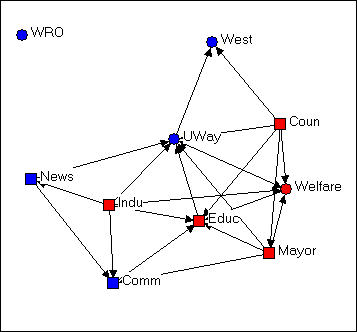
Figure 4.8. "Spring-embedding" configuration of Knoke's money network
You might immediately notice that this graph is fairly similar to the MDS solution. The algorithm uses iterative fitting (i.e. start with a random graph, measure "badness" of fit; move something, measure "badness" and if it's better keep going in that direction...) to locate the points in such a way as to put those with smallest path lengths to one another closest in the graph. This approach can often locate points very close together, and make for a graph that is hard to read. In the current example, we've also selected the optional "node repulsion" criterion that creates separation between objects that would otherwise be located very close to one another. We've also used the optional criterion of seeking to make the paths of "equal edge length" so that the distances between adjacent objects are similar.
The result is a graph that preserves many of the features of the dimensional scaling approach (distances are still somewhat interpretable; directions are often interpretable), but is usually easier to read -- particularly if it matters which specific nodes are where (rather than node types of clusters).
There is no one "right way" to use space in a graph. But one can usually do much better than a random configuration -- particularly if one has some prior hypotheses or research questions about the kinds of patterns that would be meaningful.


