5.S: Decimals (Summary)
- Page ID
- 6458
Key Terms
| circumference of a circle | The distance around a circle |
| diameter of a circle | A line segment that passes through a circle’s center connecting two points on the circle. |
| equivalent decimals | Two decimals are equivalent decimals if they convert to equivalent fractions. |
| mean | The mean of a set of n numbers is the arithmetic average of the numbers.$$mean = \dfrac{sum\; of\; values\; in\; data\; set}{n}$$ |
| median | The median of a set of data values is the middle value. Half the data values are less than or equal to the median. Half the data values are greater than or equal to the median. |
| mode | The mode of a set of numbers is the number with the highest frequency. |
| radius of a circle | A line segment from the center to any point on the circle. |
| rate | A comparison of two quantities with different units. A rate is usually written as a fraction. |
| ratio | A comparison of two numbers or two quantities that are measured with the same unit. The ratio of a to b is written a to b, \(\dfrac{a}{b}\), or a : b. |
| repeating decimal | A decimal in which the last digit or group of digits repeats endlessly. |
| unit price | A unit rate that gives the price of one item. |
| unit rate | A rate with denominator of 1 unit. |
Key Concepts
5.1 - Decimals
- Name a decimal number.
- Name the number to the left of the decimal point.
- Write “and” for the decimal point.
- Name the “number” part to the right of the decimal point as if it were a whole number.
- Name the decimal place of the last digit.
- Write a decimal number from its name.
- Look for the word “and”—it locates the decimal point. Place a decimal point under the word “and.” Translate the words before “and” into the whole number and place it to the left of the decimal point. If there is no “and,” write a “0” with a decimal point to its right.
- Mark the number of decimal places needed to the right of the decimal point by noting the place value indicated by the last word.
- Translate the words after “and” into the number to the right of the decimal point. Write the number in the spaces—putting the final digit in the last place.
- Fill in zeros for place holders as needed.
- Convert a decimal number to a fraction or mixed number.
- Look at the number to the left of the decimal. If it is zero, the decimal converts to a proper fraction. If it is not zero, the decimal converts to a mixed number. Write the whole number.
- Determine the place value of the final digit.
- Write the fraction. numerator—the ‘numbers’ to the right of the decimal point denominator—the place value corresponding to the final digit
- Simplify the fraction, if possible.
- Order decimals.
- Check to see if both numbers have the same number of decimal places. If not, write zeros at the end of the one with fewer digits to make them match.
- Compare the numbers to the right of the decimal point as if they were whole numbers.
- Order the numbers using the appropriate inequality sign.
- Round a decimal.
- Locate the given place value and mark it with an arrow.
- Underline the digit to the right of the given place value.
- Is this digit greater than or equal to 5? Yes - add 1 to the digit in the given place value. No - do not change the digit in the given place value
- Rewrite the number, removing all digits to the right of the given place value.
5.2 - Decimal Operations
- Add or subtract decimals.
- Write the numbers vertically so the decimal points line up.
- Use zeros as place holders, as needed.
- Add or subtract the numbers as if they were whole numbers. Then place the decimal in the answer under the decimal points in the given numbers.
- Multiply decimal numbers.
- Determine the sign of the product.
- Write the numbers in vertical format, lining up the numbers on the right.
- Multiply the numbers as if they were whole numbers, temporarily ignoring the decimal points.
- Place the decimal point. The number of decimal places in the product is the sum of the number of decimal places in the factors. If needed, use zeros as placeholders.
- Write the product with the appropriate sign.
- Multiply a decimal by a power of 10.
- Move the decimal point to the right the same number of places as the number of zeros in the power of 10.
- Write zeros at the end of the number as placeholders if needed.
- Divide a decimal by a whole number.
- Write as long division, placing the decimal point in the quotient above the decimal point in the dividend.
- Divide as usual.
- Divide decimal numbers.
- Determine the sign of the quotient.
- Make the divisor a whole number by moving the decimal point all the way to the right. Move the decimal point in the dividend the same number of places to the right, writing zeros as needed.
- Divide. Place the decimal point in the quotient above the decimal point in the dividend.
- Write the quotient with the appropriate sign.
- Strategy for Applications
- Identify what you are asked to find.
- Write a phrase that gives the information to find it.
- Translate the phrase to an expression.
- Simplify the expression.
- Answer the question with a complete sentence.
5.3 - Decimals and Fractions
- Convert a Fraction to a Decimal: To convert a fraction to a decimal, divide the numerator of the fraction by the denominator of the fraction.
- Properties of Circles
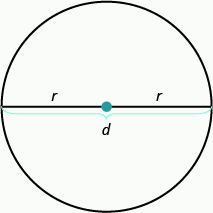
r is the length of the radius
d is the length of the diameter
The circumference is 2\(\pi\)r.\[C = 2 \pi r\]
The area is \(\pi\)r2.\[A= \pi r^{2}\]
5.4 - Solve Equations with Decimals
- Determine whether a number is a solution to an equation.
- Substitute the number for the variable in the equation.
- Simplify the expressions on both sides of the equation.
- Determine whether the resulting equation is true. If so, the number is a solution. If not, the number is not a solution.
- Properties of Equality
|
Subtraction Property of Equality For any numbers a, b, and c, if a = b then a − c = b − c. |
Addition Property of Equality For any numbers a, b, and c, if a = b then a + c = b + c. |
|
Division of Property of Equality For any numbers a, b, and c ≠ 0, if a = b then \(\dfrac{a}{c} = \dfrac{b}{c}). |
Multiplication Property of Equality For any numbers a, b, and c, if a = b then a • c = b • c. |
5.5 - Averages and Probability
- Calculate the mean of a set of numbers.
- Write the formula for the mean$$mean = \dfrac{sum\; of\; values\; in\; data\; set}{n}$$
- Find the sum of all the values in the set. Write the sum in the numerator.
- Count the number, n, of values in the set. Write this number in the denominator.
- Simplify the fraction.
- Check to see that the mean is reasonable. It should be greater than the least number and less than the greatest number in the set.
- Find the median of a set of numbers.
- List the numbers from least to greatest.
- Count how many numbers are in the set. Call this n.
- Is n odd or even? If n is an odd number, the median is the middle value. If n is an even number, the median is the mean of the two middle values.
- Identify the mode of a set of numbers.
- List the data values in numerical order.
- Count the number of times each value appears.
- The mode is the value with the highest frequency.
5.7 - Simplify and Use Square Roots
- Square Root Notation: \(\sqrt{m}\) is read ‘the square root of m ’
- If m = n2, then \(\sqrt{m}\) = n, for n ≥ 0 .
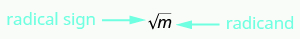
- Use a strategy for applications with square roots.
- Identify what you are asked to find.
- Write a phrase that gives the information to find it.
- Translate the phrase to an expression.
- Simplify the expression.
- Write a complete sentence that answers the question.
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."


