2.1: The Slope of a Function
- Page ID
- 462
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Suppose that \(y\) is a function of \(x\), say \(y = f(x)\). It is often necessary to know how sensitive the value of \(y\) is to small changes in \(x\).
Take, for example, \( y=f(x)=\sqrt{625-x^2}\) (the upper semicircle of radius 25 centered at the origin). When \(x=7\), we find that \( y=\sqrt{625-49}=24\). Suppose we want to know how much \(y\) changes when \(x\) increases a little, say to 7.1 or 7.01.
Solution
In the case of a straight line \(y=mx+b\), the slope \(m=\Delta y/\Delta x\) measures the change in \(y\) per unit change in \(x\). This can be interpreted as a measure of "sensitivity''; for example, if \(y=100x+5\), a small change in \(x\) corresponds to a change one hundred times as large in \(y\), so \(y\) is quite sensitive to changes in \(x\).
Let us look at the same ratio \(\Delta y/\Delta x\) for our function \( y=f(x)=\sqrt{625-x^2}\) when \(x\) changes from 7 to \(7.1\). Here \(\Delta x=7.1-7=0.1\) is the change in \(x\), and
\[ \eqalign{ \Delta y =f(x+\Delta x)-f(x)&=f(7.1)-f(7)\cr &=\sqrt{625-7.1^2}-\sqrt{625-7^2}\approx 23.9706-24=-0.0294.\cr } \nonumber \]
Thus, \(\Delta y/\Delta x\approx -0.0294/0.1=-0.294\).
This means that \(y\) changes by less than one third the change in \(x\), so apparently \(y\) is not very sensitive to changes in \(x\) at \(x=7\). We say "apparently'' here because we don't really know what happens between 7 and \(7.1\). Perhaps \(y\) changes dramatically as \(x\) runs through the values from 7 to \(7.1\), but at \(7.1\) \(y\) just happens to be close to its value at \(7\). This is not in fact the case for this particular function, but we don't yet know why.
One way to interpret the above calculation is by reference to a line. We have computed the slope of the line through \((7,24)\) and \((7.1,23.9706)\), called a chord of the circle. In general, if we draw the chord from the point \((7,24)\) to a nearby point on the semicircle \((7+\Delta x,\,f(7+\Delta x))\), the slope of this chord is the so-called difference quotient \( \hbox{slope of chord}={f(7+\Delta x)-f(7) \over \Delta x}= {\sqrt{625-(7+\Delta x)^2}-24\over \Delta x}. \) For example, if \(x\) changes only from 7 to 7.01, then the difference quotient (slope of the chord) is approximately equal to \((23.997081-24)/0.01=-0.2919\). This is slightly less steep than the chord from \((7,24)\) to \((7.1,23.9706)\).
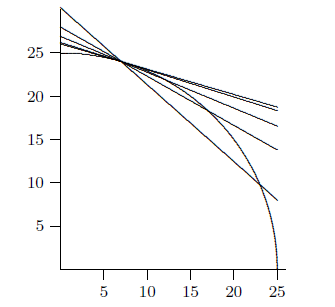
As the second value \(7+\Delta x\) moves in towards 7, the chord joining \((7,f(7))\) to \((7+\Delta x,f(7+\Delta x))\) shifts slightly. As indicated in figure 2.1.1, as \(\Delta x\) gets smaller and smaller, the chord joining \((7,24)\) to \((7+\Delta x,f(7+\Delta x))\) gets closer and closer to the tangent line to the circle at the point \((7,24)\). (Recall that the tangent line is the line that just grazes the circle at that point, i.e., it doesn't meet the circle at any second point.) Thus, as \(\Delta x\) gets smaller and smaller, the slope \(\Delta y/\Delta x\) of the chord gets closer and closer to the slope of the tangent line. This is actually quite difficult to see when \(\Delta x\) is small, because of the scale of the graph. The values of \(\Delta x\) used for the figure are \(1\), \(5\), \(10\) and \(15\), not really very small values. The tangent line is the one that is uppermost at the right hand endpoint.
So far we have found the slopes of two chords that should be close to the slope of the tangent line, but what is the slope of the tangent line exactly? Since the tangent line touches the circle at just one point, we will never be able to calculate its slope directly, using two "known'' points on the line. What we need is a way to capture what happens to the slopes of the chords as they get "closer and closer'' to the tangent line.
Instead of looking at more particular values of \(\Delta x\), let's see what happens if we do some algebra with the difference quotient using just \(\Delta x\). The slope of a chord from \((7,24)\) to a nearby point is given by
\[ \eqalign{ {\sqrt{625-(7+\Delta x)^2} - 24\over \Delta x}&= {\sqrt{625-(7+\Delta x)^2} - 24\over \Delta x}{\sqrt{625-(7+\Delta x)^2}+24\over \sqrt{625-(7+\Delta x)^2}+24}\cr& ={625-(7+\Delta x)^2-24^2\over \Delta x(\sqrt{625-(7+\Delta x)^2}+24)}\cr& ={49-49-14\Delta x-\Delta x^2\over \Delta x(\sqrt{625-(7+\Delta x)^2}+24)}\cr& ={\Delta x(-14-\Delta x)\over \Delta x(\sqrt{625-(7+\Delta x)^2}+24)}\cr& = {-14-\Delta x\over\sqrt{625-(7+\Delta x)^2}+24}\cr } \nonumber \]
Now, can we tell by looking at this last formula what happens when \(\Delta x\) gets very close to zero? The numerator clearly gets very close to \(-14\) while the denominator gets very close to \( \sqrt{625-7^2}+24=48\). Is the fraction therefore very close to \(-14/48 = -7/24 \cong -0.29167\)? It certainly seems reasonable, and in fact it is true: as \(\Delta x\) gets closer and closer to zero, the difference quotient does in fact get closer and closer to \(-7/24\), and so the slope of the tangent line is exactly \(-7/24\).
What about the slope of the tangent line at \(x=12\)? Well, 12 can't be all that different from 7; we just have to redo the calculation with 12 instead of 7. This won't be hard, but it will be a bit tedious. What if we try to do all the algebra without using a specific value for \(x\)? Let's copy from above, replacing 7 by \(x\). We'll have to do a bit more than that---for example, the "24'' in the calculation came from \( \sqrt{625-7^2}\), so we'll need to fix that too.
\[ \eqalign{& {\sqrt{625-(x+\Delta x)^2} - \sqrt{625-x^2}\over \Delta x}=\cr \qquad&={\sqrt{625-(x+\Delta x)^2} - \sqrt{625-x^2}\over \Delta x}{\sqrt{625-(x+\Delta x)^2}+\sqrt{625-x^2}\over \sqrt{625-(x+\Delta x)^2}+\sqrt{625-x^2}}\cr& ={625-(x+\Delta x)^2-625+x^2\over \Delta x(\sqrt{625-(x+\Delta x)^2}+\sqrt{625-x^2})}\cr& ={625-x^2-2x\Delta x-\Delta x^2-625+x^2\over \Delta x(\sqrt{625-(x+\Delta x)^2}+\sqrt{625-x^2})}\cr& ={\Delta x(-2x-\Delta x)\over \Delta x(\sqrt{625-(x+\Delta x)^2}+\sqrt{625-x^2})}\cr& = {-2x-\Delta x\over\sqrt{625-(x+\Delta x)^2}+\sqrt{625-x^2}}\cr } \nonumber \]
Now what happens when \(\Delta x\) is very close to zero? Again it seems apparent that the quotient will be very close to \({-2x\over \sqrt{625-x^2}+\sqrt{625-x^2}} ={-2x\over 2\sqrt{625-x^2}}={-x\over \sqrt{625-x^2}}. \) Replacing \(x\) by 7 gives \(-7/24\), as before, and now we can easily do the computation for 12 or any other value of \(x\) between \(-25\) and 25.
So now we have a single, simple formula, \( {-x/ \sqrt{625-x^2}}\), that tells us the slope of the tangent line for any value of \(x\). This slope, in turn, tells us how sensitive the value of \(y\) is to changes in the value of \(x\).
What do we call such a formula? That is, a formula with one variable, so that substituting an "input'' value for the variable produces a new "output'' value? This is a function. Starting with one function, \( \sqrt{625-x^2}\), we have derived, by means of some slightly nasty algebra, a new function, \( {-x/ \sqrt{625-x^2}}\), that gives us important information about the original function. This new function in fact is called the derivative of the original function. If the original is referred to as \(f\) or \(y\) then the derivative is often written \(f'\) or \(y'\) and pronounced "f prime'' or "y prime'', so in this case we might write \(f'(x)=-x/ \sqrt{625-x^2}\). At a particular point, say \(x=7\), we say that \(f'(7)=-7/24\) or "\(f\) prime of 7 is \(-7/24\)'' or "the derivative of \(f\) at 7 is \(-7/24\).''
To summarize, we compute the derivative of \(f(x)\) by forming the difference quotient
\[ \dfrac{f(x+\Delta x)-f(x)}{ \Delta x}, \nonumber \]
which is the slope of a line, then we figure out what happens when \(\Delta x\) gets very close to 0.
We should note that in the particular case of a circle, there's a simple way to find the derivative. Since the tangent to a circle at a point is perpendicular to the radius drawn to the point of contact, its slope is the negative reciprocal of the slope of the radius. The radius joining \((0,0)\) to \((7,24)\) has slope 24/7. Hence, the tangent line has slope \(-7/24\). In general, a radius to the point \( (x,\sqrt{625-x^2})\) has slope \( \sqrt{625-x^2}/x\), so the slope of the tangent line is \( {-x/ \sqrt{625-x^2}}\), as before. It is NOT always true that a tangent line is perpendicular to a line from the origin---don't use this shortcut in any other circumstance.
As above, and as you might expect, for different values of \(x\) we generally get different values of the derivative \(f'(x)\). Could it be that the derivative always has the same value? This would mean that the slope of \(f\), or the slope of its tangent line, is the same everywhere. One curve that always has the same slope is a line; it seems odd to talk about the tangent line to a line, but if it makes sense at all the tangent line must be the line itself. It is not hard to see that the derivative of \(f(x)=mx+b\) is \(f'(x)=m\); see exercise 6.
Contributors
Integrated by Justin Marshall.


