12.5: Tangential and Normal Components of Acceleration
- Page ID
- 5530
- Describe the velocity and acceleration vectors of a particle moving in space.
- Explain the tangential and normal components of acceleration.
- State Kepler’s laws of planetary motion.
We have now seen how to describe curves in the plane and in space, and how to determine their properties, such as arc length and curvature. All of this leads to the main goal of this chapter, which is the description of motion along plane curves and space curves. We now have all the tools we need; in this section, we put these ideas together and look at how to use them.
Motion Vectors in the Plane and in Space
Our starting point is using vector-valued functions to represent the position of an object as a function of time. All of the following material can be applied either to curves in the plane or to space curves. For example, when we look at the orbit of the planets, the curves defining these orbits all lie in a plane because they are elliptical. However, a particle traveling along a helix moves on a curve in three dimensions.
Let \(\vecs r(t)\) be a twice-differentiable vector-valued function of the parameter \(t\) that represents the position of an object as a function of time.
The velocity vector \(\vecs v(t)\) of the object is given by
\[\text{Velocity}\,=\vecs v(t)=\vecs r^{\,\prime}(t). \label{Eq1} \]
The acceleration vector \(\vecs a(t)\) is defined to be
\[\text{Acceleration}\,=\vecs a(t)=\vecs v^{\,\prime}(t)=\vecs r^{\,\prime\prime}(t). \label{Eq2} \]
The speed is defined to be
\[\mathrm{Speed}\,=v(t)=‖\vecs v(t)‖=‖\vecs r^{\,\prime}(t)‖=\dfrac{ds}{dt}. \label{Eq3} \]
Since \(\vecs{r}(t)\) can be in either two or three dimensions, these vector-valued functions can have either two or three components. In two dimensions, we define \(\vecs{r}(t)=x(t) \hat{\mathbf i}+y(t) \hat{\mathbf j}\) and in three dimensions \(\vecs r(t)=x(t) \hat{\mathbf i}+y(t) \hat{\mathbf j}+z(t) \hat{\mathbf k}\). Then the velocity, acceleration, and speed can be written as shown in the following table.
| Quantity | Two Dimensions | Three Dimensions |
|---|---|---|
| Position | \(\vecs{r}(t)=x(t) \hat{\mathbf i}+y(t) \hat{\mathbf j}\) | \(\vecs{r}(t)=x(t) \hat{\mathbf i}+y(t) \hat{\mathbf j}+z(t) \hat{\mathbf k}\) |
| Velocity | \(\vecs{v}(t)=x^{\,\prime}(t) \hat{\mathbf i}+y^{\,\prime}(t) \hat{\mathbf j}\) | \(\vecs{v}(t)=x^{\,\prime}(t) \hat{\mathbf i}+y^{\,\prime}(t) \hat{\mathbf j}+z^{\,\prime}(t) \hat{\mathbf k}\) |
| Acceleration | \(\vecs{a}(t)=x^{\,\prime\prime}(t) \hat{\mathbf i}+y^{\,\prime\prime}(t) \hat{\mathbf j}\) | \(\vecs{a}(t)=x^{\,\prime\prime}(t) \hat{\mathbf i}+y^{\,\prime\prime}(t) \hat{\mathbf j}+z^{\,\prime\prime}(t) \hat{\mathbf k}\) |
| Speed | \(\|\vecs{v}(t)\|= \sqrt{(x^{\,\prime}(t))^2+(y^{\,\prime}(t))^2}\) | \(\|\vecs{v}(t)\|=\sqrt{(x^{\,\prime}(t))^2+(y^{\,\prime}(t))^2+(z^{\,\prime}(t))^2}\) |
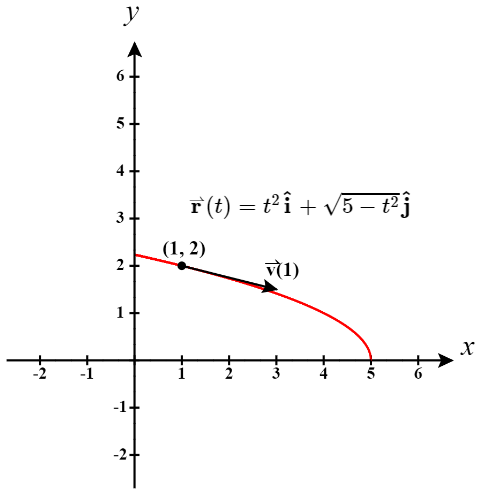
A particle moves in a parabolic path defined by the vector-valued function \(\vecs{r}(t)=t^2 \hat{\mathbf i}+ \sqrt{5−t^2} \hat{\mathbf j}\), where \(t\) measures time in seconds.
- Find the velocity, acceleration, and speed as functions of time.
- Sketch the curve along with the velocity vector at time \(t=1\).
Solution
- We use Equations \ref{Eq1}, \ref{Eq2}, and \ref{Eq3}:
\[ \begin{align*} \vecs{v}(t) &= \vecs{r}^{\,\prime}(t)=2t\hat{\mathbf i}−\dfrac{t}{\sqrt{5-t^2}}\hat{\mathbf j} \\[4pt] \vecs{a}(t) &=\vecs{v}^{\,\prime}(t)=2\hat{\mathbf i}−5(5−t^2)^{-\frac{3}{2}}\hat{\mathbf j} \\[4pt] ||\vecs{v}(t)|| &=||\vecs{r}^{\,\prime}(t)|| \\[4pt] &=\sqrt{(2t)^2+\left(-\dfrac{t}{\sqrt{5-t^2}}\right)^2} \\[4pt] &=\sqrt{4t^2+\dfrac{t^2}{5-t^2}} \\[4pt] &=\sqrt{\dfrac{21t^2-4t^4}{5-t^2}}. \end{align*}\]
- The graph of \(\vecs{r}(t)=t^2 \hat{\mathbf i}+ \sqrt{5−t^2} \hat{\mathbf j}\) is a portion of a parabola (Figure \(\PageIndex{1}\)).
When \(t=1\), \(\vecs r(1) = (1)^2 \mathbf{\hat i} + \sqrt{5-(1)^2} \mathbf{\hat j} \quad = \quad \mathbf{\hat i} + \sqrt{4} \mathbf{\hat j} \quad = \quad \mathbf{\hat i} + 2 \mathbf{\hat j}\).
Thus the particle would be located at the point \((1, 2)\) when \(t =1\).
The velocity vector at \(t=1\) is\[ \begin{align*} \vecs{v}(1) &=\vecs{r}^{\,\prime}(1)=2(1)\hat{\mathbf i}−\frac{1}{\sqrt{5-1^2}} \hat{\mathbf j}\quad \\[4pt] &= \quad 2\hat{\mathbf i}−\frac{1}{2}\hat{\mathbf j} \end{align*}\]
and the acceleration vector at \(t=1\) is\[\vecs{a}(1)=\vecs{v}^{\,\prime}(1)=2\hat{\mathbf i}−5(5 - 1^2)^{-3/2}\hat{\mathbf j}\quad = \quad 2\hat{\mathbf i}−\frac{5}{8}\hat{\mathbf j}. \nonumber \]
Notice that the velocity vector is tangent to the path, as is always the case.
A particle moves in a path defined by the vector-valued function \(\vecs r(t)=(t^2−3t)\,\hat{\mathbf i}+(2t−4)\,\hat{\mathbf j}+(t+2)\,\hat{\mathbf k}\), where \(t\) measures time in seconds and where distance is measured in feet. Find the velocity, acceleration, and speed as functions of time.
- Hint
-
Use Equations \ref{Eq1}, \ref{Eq2}, and \ref{Eq3}.
- Answer
-
\[\begin{align*}\vecs v(t) &=\vecs{r}^{\,\prime}(t) =(2t-3)\,\hat{\mathbf i}+2\,\hat{\mathbf j}+\,\hat{\mathbf k}\\[4pt] \vecs a(t) &=\vecs v^{\,\prime}(t) =2\,\hat{\mathbf i} \end{align*}\]
\[ ||\vecs{r}^{\,\prime}(t)||=\sqrt{(2t-3)^2+2^2+1^2} =\sqrt{4t^2-12t+14} \nonumber \]
The units for velocity and speed are feet per second, and the units for acceleration are feet per second squared.
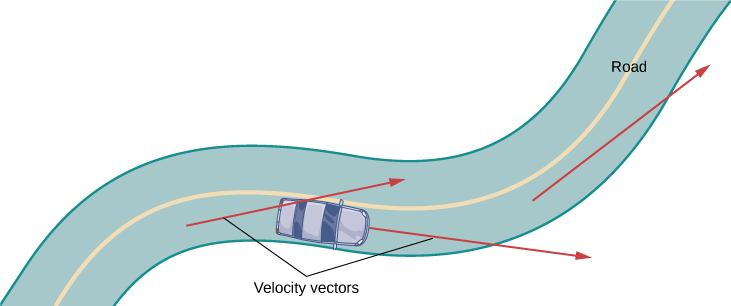
To gain a better understanding of the velocity and acceleration vectors, imagine you are driving along a curvy road. If you do not turn the steering wheel, you would continue in a straight line and run off the road. The speed at which you are traveling when you run off the road, coupled with the direction, gives a vector representing your velocity, as illustrated in Figure \(\PageIndex{2}\).
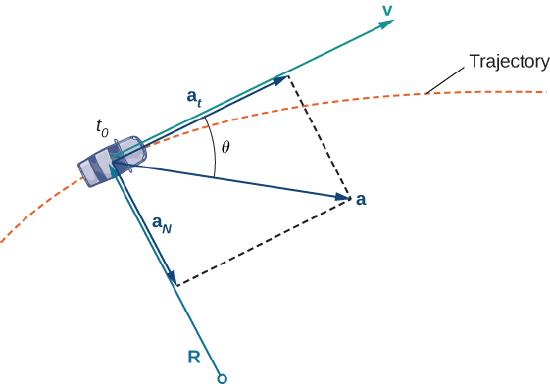
However, the fact that you must turn the steering wheel to stay on the road indicates that your velocity is always changing (even if your speed is not) because your direction is constantly changing to keep you on the road. As you turn to the right, your acceleration vector also points to the right. As you turn to the left, your acceleration vector points to the left. This indicates that your velocity and acceleration vectors are constantly changing, regardless of whether your actual speed varies (Figure \(\PageIndex{3}\)).
Components of the Acceleration Vector
We can combine some of the concepts discussed in Arc Length and Curvature with the acceleration vector to gain a deeper understanding of how this vector relates to motion in the plane and in space. Recall that the unit tangent vector \(\vecs T\) and the unit normal vector \(\vecs N\) form an osculating plane at any point \(P\) on the curve defined by a vector-valued function \(\vecs{r}(t)\). The following theorem shows that the acceleration vector \(\vecs{a}(t)\) lies in the osculating plane and can be written as a linear combination of the unit tangent and the unit normal vectors.
The acceleration vector \(\vecs{a}(t)\) of an object moving along a curve traced out by a twice-differentiable function \(\vecs{r}(t)\) lies in the plane formed by the unit tangent vector \(\vecs T(t)\) and the principal unit normal vector \(\vecs N(t)\) to \(C\). Furthermore,
\[\vecs{a}(t) = v^{\,\prime}(t)\vecs{T}(t) + [v(t)]^2 \kappa \vecs{N}(t) \nonumber \]
Here, \(v(t) = \|\vecs v(t)\|\) is the speed of the object and \(\kappa\) is the curvature of \(C\) traced out by \(\vecs{r}(t)\).
Because \(\vecs{v}(t)=\vecs{r}^{\,\prime}(t)\) and \(\vecs{T}(t)=\dfrac{\vecs{r}^{\,\prime}(t)}{||\vecs{r}^{\,\prime}(t)||}\), we have \(\vecs v(t)=||\vecs{r}^{\,\prime}(t)||\vecs{T}(t)=v(t)\vecs{T}(t)\).
Now we differentiate this equation:
\[\vecs{a}(t)=\vecs{v}^{\,\prime}(t)=\dfrac{d}{dt}\left(v(t)\vecs{T}(t)\right)=v^{\,\prime}(t)\vecs{T}(t)+v(t)\vecs{T}^{\,\prime}(t) \nonumber \]
Since \(\vecs{N}(t)=\dfrac{\vecs{T}^{\,\prime}(t)}{||\vecs{T}^{\,\prime}(t)||}\), we know \(\vecs{T}^{\,\prime}(t)=||\vecs{T}^{\,\prime}(t)||\vecs{N}(t)\), so
\[\vecs{a}(t)=v^{\,\prime}(t)\vecs{T}(t)+v(t)||\vecs{T}^{\,\prime}(t)||\vecs{N}(t). \nonumber \]
A formula for curvature is \(\kappa=\dfrac{||\vecs{T}^{\,\prime}(t)||}{||\vecs{r}^{\,\prime}(t)||}\), so \(\vecs{T}^{\,\prime}(t) = \kappa ||\vecs{r}^{\,\prime}(t) || = \kappa v(t) \).
This gives \(\vecs{a}(t)=v^{\,\prime}(t)\vecs{T}(t)+\kappa (v(t))^2 \vecs{N}(t).\)
\(\square\)
The coefficients of \(\vecs{T}(t)\) and \(\vecs{N}(t)\) are referred to as the tangential component of acceleration and the normal component of acceleration, respectively. We write \(a_\vecs{T}\) to denote the tangential component and \(a_\vecs{N}\) to denote the normal component.
Let \(\vecs{r}(t)\) be a vector-valued function that denotes the position of an object as a function of time. Then \(\vecs{a}(t)=\vecs{r}′^{\,\prime}(t)\) is the acceleration vector. The tangential and normal components of acceleration \(a_\vecs{T}\) and \(a_\vecs{N}\) are given by the formulas
\[a_{\vecs{T}}=\vecs a \cdot\vecs{T}=\dfrac{\vecs{v}\cdot\vecs{a}}{||\vecs{v}||} \label{Eq1B} \]
and
\[a_\vecs{N}=\vecs a\cdot \vecs N=\dfrac{||\vecs v \times \vecs a||}{||\vecs v||}=\sqrt{||\vecs a||^2−{\left(a_{\vecs{T}}\right)^2}}. \label{Eq2B} \]
These components are related by the formula
\[\vecs{a}(t)=a_\vecs{T} \vecs{T}(t)+a_\vecs{N}\vecs{N}(t). \label{Eq3B} \]
Here \(\vecs{T}(t)\) is the unit tangent vector to the curve defined by \(\vecs{r}(t)\), and \(\vecs{N}(t)\) is the unit normal vector to the curve defined by \(\vecs{r}(t)\).
The normal component of acceleration is also called the centripetal component of acceleration or sometimes the radial component of acceleration. To understand centripetal acceleration, suppose you are traveling in a car on a circular track at a constant speed. Then, as we saw earlier, the acceleration vector points toward the center of the track at all times. As a rider in the car, you feel a pull toward the outside of the track because you are constantly turning. This sensation acts in the opposite direction of centripetal acceleration. The same holds true for non-circular paths. The reason is that your body tends to travel in a straight line and resists the force resulting from acceleration that push it toward the side. Note that at point \(B\) in Figure \(\PageIndex{4}\) the acceleration vector is pointing backward. This is because the car is decelerating as it goes into the curve.
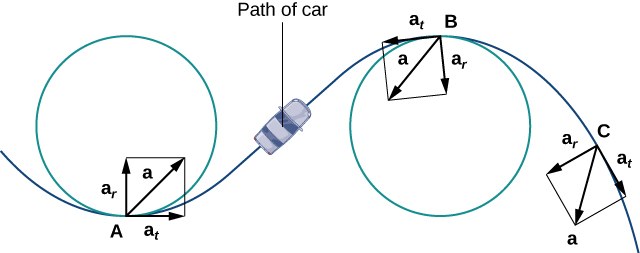
The tangential and normal unit vectors at any given point on the curve provide a frame of reference at that point. The tangential and normal components of acceleration are the projections of the acceleration vector onto \(\vecs T\) and \(\vecs N\), respectively.
A particle moves in a path defined by the vector-valued function \(\vecs{r}(t)=t^2\,\hat{\mathbf i}+(2t−3)\,\hat{\mathbf j}+(3t^2−3t)\,\hat{\mathbf k}\), where \(t\) measures time in seconds and distance is measured in feet.
- Find \(a_\vecs{T}\) and \(a_\vecs{N}\) as functions of \(t\).
- Find \(a_\vecs{T}\) and \(a_\vecs{N}\) at time \(t=2\).
Solution
- Let’s start deriving the velocityand acceleration functions:
\[\begin{align*} \vecs{v}(t) &= \vecs{r}^{\,\prime}(t) \\[4pt] &= 2t\,\hat{\mathbf i}+2\,\hat{\mathbf j}+(6t-3)\,\hat{\mathbf k} \\[4pt] \vecs{a}(t) &= \vecs{v}^{\,\prime}(t) \\[4pt] &=2\,\hat{\mathbf i}+6\,\hat{\mathbf k} \end{align*}\]Now we apply Equation \ref{Eq1B}: \[\begin{align*}a_{\vecs{T}} &=\dfrac{\vecs{v}\cdot \vecs{a}}{||\vecs{v} ||} \\[4pt] &= \dfrac{ (2t \,\hat{\mathbf i} +2\,\hat{\mathbf j} +(6t-3)\,\hat{\mathbf k})\cdot(2\,\hat{\mathbf i}+6\,\hat{\mathbf k}) }{|| 2t\,\hat{\mathbf i} + 2\,\hat{\mathbf j} + (6t-3)\,\hat{\mathbf k} ||} \\[4pt] &= \dfrac{4t + 6(6t-3)}{\sqrt{(2t)^2 +2^2 + (6t-3)^2}} \\[4pt] &= \dfrac{40t-18}{40t^2 - 36t+13} \end{align*}\] Now we can apply Equation \ref{Eq2B}:
\[\begin{align*} a_\vecs{N} &=\sqrt{||\vecs{a}||^2-\left(a_{\vecs{T}}\right)^2} \\[4pt] &= \sqrt{||2\,\hat{\mathbf i}+6\,\hat{\mathbf k}||^2 - \left( \dfrac{ 40t-18 }{\sqrt{40t^2-36t+13}} \right)^2} \\[4pt] &= \sqrt{ 4+36-\dfrac{(40t-18)^2}{40t^2-36t+13} } \\[4pt] &= \sqrt{\dfrac{ 40(40t^2-36t+13)-(1600t^2-1440t+324) }{40t^2-36t+13} } \\[4pt] &= \sqrt{ \dfrac{196}{ 40t^2-36t+13} } \\[4pt] &= \dfrac{14}{\sqrt{40t^2-36t+13}} \end{align*}\]
- We must evaluate each of the answers from part a at \(t=2\):
\[\begin{align*} a_{\vecs{T}}(2) &= \dfrac{ 40(2)-18 }{\sqrt{40(2)^2 - 36(2)+13 }} \\[4pt] &= \dfrac{80-18 }{\sqrt{160-72+13}} \\[4pt] &= \dfrac{62}{\sqrt{101}} \\[4pt] a_{\vecs{N}}(2) &= \dfrac{14}{\sqrt{40(2)^2 -36(2)+13 }} \\[4pt] &= \dfrac{14}{\sqrt{160-72+13}} = \dfrac{14}{\sqrt{101}}. \end{align*}\]
The units of acceleration are feet per second squared, as are the units of the normal and tangential components of acceleration.
An object moves in a path defined by the vector-valued function \(\vecs r(t)=4t\,\hat{\mathbf i}+t^2\,\hat{\mathbf j}\), where \(t\) measures time in seconds.
- Find \(a_\vecs{T}\) and \(a_\vecs{N}\) as functions of \(t\).
- Find \(a_\vecs{T}\) and \(a_\vecs{N}\) at time \(t=−3\).
- Hint
-
Use Equations \ref{Eq1B} and \ref{Eq2B}
- Answer
-
a. \[\begin{align*} a_\vecs{T} =\dfrac{\vecs v(t) \cdot \vecs a(t)}{||\vecs v(t)||}= \dfrac{\vecs r^{\,\prime}(t) \cdot \vecs r'^{\,\prime}(t) }{||\vecs r^{\,\prime}(t)||} \\ = \dfrac{ (4\,\hat{\mathbf i} + 2t \,\hat{\mathbf j}) \cdot (2\,\hat{\mathbf j}) }{||4\,\hat{\mathbf i} + 2t \,\hat{\mathbf j} ||} \\ = \dfrac{4t}{\sqrt{4^2 + (2t)^2}}\\ = \dfrac{2t}{\sqrt{2+t^2}} \end{align*}\]
\[\begin{align*} a_\vecs{N} = \sqrt{||\vecs a||^2-a_\vecs{T}^2}\\ =\sqrt{||2\,\hat{\mathbf j} ||^2 - \left(\dfrac{2t}{\sqrt{2+t^2}}\right)^2} \\ =\sqrt{ 4 - \dfrac{4t^2 }{2+t^2} } \end{align*}\]b. \[\begin{align*} a_\vecs{T}(−3) = \dfrac{2(-3)}{\sqrt{2+(-3)^2}} \\ = \dfrac{-6}{\sqrt{11}}\end{align*}\]
\[\begin{align*}a_\vecs{N}(−3) = \sqrt{ 4 - \dfrac{4(-3)^2 }{2+(-3)^2} } \\ = \sqrt{4- \dfrac{36}{11}} \\ = \sqrt{\dfrac{8}{11} }\\ =\dfrac{2\sqrt{2}}{\sqrt{11}} \end{align*}\]
Projectile Motion
Now let’s look at an application of vector functions. In particular, let’s consider the effect of gravity on the motion of an object as it travels through the air, and how it determines the resulting trajectory of that object. In the following, we ignore the effect of air resistance. This situation, with an object moving with an initial velocity but with no forces acting on it other than gravity, is known as projectile motion. It describes the motion of objects from golf balls to baseballs, and from arrows to cannonballs.
First we need to choose a coordinate system. If we are standing at the origin of this coordinate system, then we choose the positive \(y\)-axis to be up, the negative \(y\)-axis to be down, and the positive \(x\)-axis to be forward (i.e., away from the thrower of the object). The effect of gravity is in a downward direction, so Newton’s second law tells us that the force on the object resulting from gravity is equal to the mass of the object times the acceleration resulting from gravity, or \(\vecs F_g=m\vecs a\), where \(\vecs F_g\) represents the force from gravity and \(\vecs a = -g\,\hat{\mathbf j}\) represents the acceleration resulting from gravity at Earth’s surface. The value of \(g\) in the English system of measurement is approximately 32 ft/sec2 and it is approximately 9.8 m/sec2 in the metric system. This is the only force acting on the object. Since gravity acts in a downward direction, we can write the force resulting from gravity in the form \(\vecs F_g=−mg\,\hat{\mathbf j}\), as shown in Figure \(\PageIndex{5}\).
Newton’s second law also tells us that \(F=m\vecs{a}\), where \(\vecs a\) represents the acceleration vector of the object. This force must be equal to the force of gravity at all times, so we therefore know that
\[\begin{align*} \vecs F =\vecs F_g \\ m\vecs{a} = -mg \,\hat{\mathbf j} \\ \vecs{a} = -g\,\hat{\mathbf j}. \end{align*}\]
Now we use the fact that the acceleration vector is the first derivative of the velocity vector. Therefore, we can rewrite the last equation in the form
\[\vecs v^{\,\prime}(t) = -g\,\hat{\mathbf j} \nonumber \]
By taking the antiderivative of each side of this equation we obtain
\[ \vecs v(t) = \int -g \,\hat{\mathbf j}\; dt = -gt\,\hat{\mathbf j} + \vecs C_1 \nonumber \]
for some constant vector \(\vecs C_1\). To determine the value of this vector, we can use the velocity of the object at a fixed time, say at time \(t=0\). We call this velocity the initial velocity: \(\vecs v(0)=\vecs v_0\). Therefore, \(\vecs v(0)=−g(0)\,\hat{\mathbf j}+\vecs C_1=\vecs v_0\) and \(\vecs C_1= \vecs v_0\). This gives the velocity vector as \(\vecs v(t)=−gt\,\hat{\mathbf j}+\vecs v_0\).
Next we use the fact that velocity \(\vecs{v}(t)\) is the derivative of position \(\vecs{s}(t)\). This gives the equation
\[\vecs s^{\,\prime}(t)=-gt\,\hat{\mathbf j}+\vecs{v}_0. \nonumber \]
Taking the antiderivative of both sides of this equation leads to
\[\begin{align*} \vecs s(t) &= \int -gt\,\hat{\mathbf j} + \vecs{v}_0 \;dt \\[4pt] &= -\dfrac{1}{2}gt^2 \,\hat{\mathbf j} + \vecs{v}_0 t + \vecs{C}_2 \end{align*}\]
with another unknown constant vector \(\vecs{C}_2\). To determine the value of \(\vecs{C}_2\), we can use the position of the object at a given time, say at time \(t=0\). We call this position the initial position: \(\vecs{s}(0)=\vecs{s}_0\). Therefore, \(\vecs{s}(0)=−(1/2)g(0)^2\,\hat{\mathbf j}+\vecs{v}_0(0)+\vecs{C}_2=\vecs{s}_0\). This gives the position of the object at any time as
\[ \vecs{s}(t)=−\dfrac{1}{2}gt^2 \,\hat{\mathbf j}+\vecs{v}_0 t+\vecs{s}_0. \nonumber \]
Let’s take a closer look at the initial velocity and initial position. In particular, suppose the object is thrown upward from the origin at an angle \(\theta\) to the horizontal, with initial speed \(\vecs{v}_0\). How can we modify the previous result to reflect this scenario? First, we can assume it is thrown from the origin. If not, then we can move the origin to the point from where it is thrown. Therefore, \(\vecs{s}_0=\vecs{0}\), as shown in Figure \(\PageIndex{6}\).
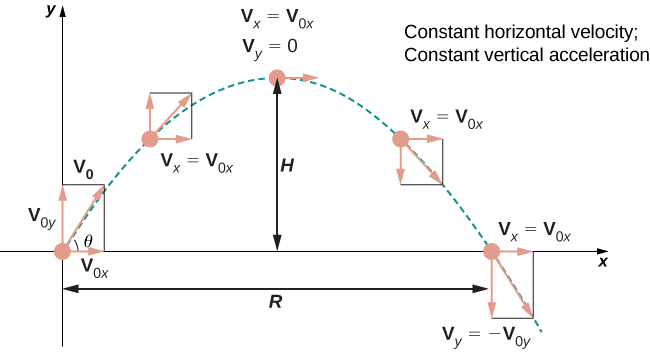
We can rewrite the initial velocity vector in the form \(\vecs{v}_0= v_0 \cos \theta \,\hat{\mathbf i} + v_0 \sin \theta \,\hat{\mathbf j}\). Then the equation for the position function \(\vecs{s}(t)\) becomes
\[\begin{align*} \vecs{s}(t) &=-\dfrac{1}{2} gt^2\,\hat{\mathbf j} + v_0 t \cos\theta \,\hat{\mathbf i} + v_0 t \sin\theta \,\hat{\mathbf j} \\[4pt] &= v_0 t \cos\theta\,\hat{\mathbf i} + v_0 t \sin\theta \,\hat{\mathbf j} - \dfrac{1}{2} gt^2\,\hat{\mathbf j} \\[4pt] &= v_0 t \cos\theta \,\hat{\mathbf i} + \left(v_0 t \sin\theta - \dfrac{1}{2} gt^2\right)\,\hat{\mathbf j}. \end{align*}\]
The coefficient of \(\hat{\mathbf i}\) represents the horizontal component of \(\vecs{s}(t)\) and is the horizontal distance of the object from the origin at time \(t\). The maximum value of the horizontal distance (measured at the same initial and final altitude) is called the range \(R\). The coefficient of \(\hat{\mathbf j}\) represents the vertical component of \(\vecs{s}(t)\) and is the altitude of the object at time \(t\). The maximum value of the vertical distance is the height \(H\).
During an Independence Day celebration, a cannonball is fired from a cannon on a cliff toward the water. The cannon is aimed at an angle of 30° above horizontal and the initial speed of the cannonball is 600 ft/sec. The cliff is 100 ft above the water (Figure \(\PageIndex{7}\)).
- Find the maximum height of the cannonball.
- How long will it take for the cannonball to splash into the sea?
- How far out to sea will the cannonball hit the water?
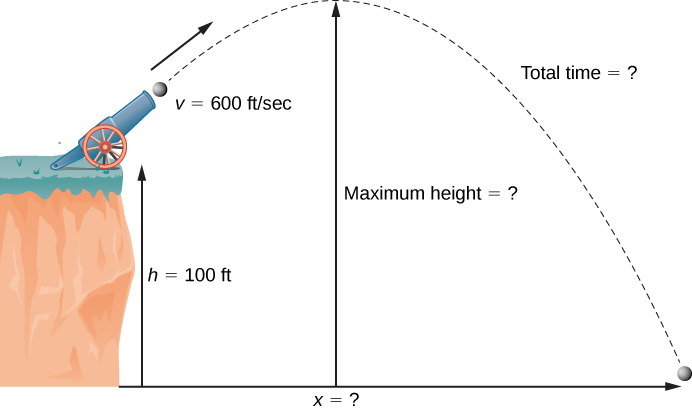
Solution
We use the equation
\[\vecs{s}(t) = v_0 t \cos\theta \,\hat{\mathbf i} + \left(v_0 t \sin\theta - \dfrac{1}{2}gt^2 \right)\,\hat{\mathbf j} \nonumber \]
with \(\theta=30^\circ \), \(g=32 \dfrac{\text{ft}}{\text{sec}^2}\), and \(v_0=600 \dfrac{\text{ft}}{\text{sec}}\). Then the position equation becomes
\[\begin{align*} \vecs{s}(t) &= 600 t ( \cos 30^\circ)\,\hat{\mathbf i} + \left(600t \sin30^\circ - \dfrac{1}{2}(32)t^2 \right)\,\hat{\mathbf j} \\[4pt] &= 300t\sqrt{3} \,\hat{\mathbf i} + \left( 300t - 16t^2 \right)\,\hat{\mathbf j} \end{align*}\]
- The cannonball reaches its maximum height when the vertical component of its velocity is zero, because the cannonball is neither rising nor falling at that point. The velocity vector is
\[\begin{align*} \vecs{v}(t) &=\vecs s^{\,\prime}(t)\\[4pt] &= 300 \sqrt{3} \,\hat{\mathbf i} + (300-32t)\,\hat{\mathbf j} \end{align*} \nonumber \]
Therefore, the vertical component of velocity is given by the expression \(300−32t\). Setting this expression equal to zero and solving for \(t\) gives \(t=9.375\) sec. The height of the cannonball at this time is given by the vertical component of the position vector, evaluated at \(t=9.375\).\[\begin{align*} \vecs{s}(9.375) &=300(9.375)\sqrt{3}\,\hat{\mathbf i}+(300(9.375)−16(9.375)^2)\,\hat{\mathbf j} \\[4pt] &=4871.39 \,\hat{\mathbf i}+1406.25\,\hat{\mathbf j} \end{align*}\]
Therefore, the maximum height of the cannonball is 1406.39 ft above the cannon, or 1506.39 ft above sea level. - When the cannonball lands in the water, it is 100 ft below the cannon. Therefore, the vertical component of the position vector is equal to \(−100.\) Setting the vertical component of \(\vecs s(t)\) equal to \(−100\) and solving, we obtain
\[\begin{align*} 300t-16t^2 &= -100 \\ 16t^2-300t-100 =0 \\4t^2-75-25 =0 \\[4pt] t &= \dfrac{75\pm \sqrt{(-75)^2}-4(4)(-25) }{2(4)} \\[4pt] &= \dfrac{75 \pm \sqrt{6025}}{8} \\[4pt] &= \dfrac{75 \pm 5\sqrt{241}}{8} \end{align*}\]
The positive value of \(t\) that solves this equation is approximately 19.08. Therefore, the cannonball hits the water after approximately 19.08 sec. - To find the distance out to sea, we simply substitute the answer from part (b) into \(\vecs{s}(t)\):
\[\begin{align*} \vecs s(19.08) &=300(19.08)\sqrt{3} \,\hat{\mathbf i}+\left(300(19.08)−16(19.08)^2\right)\,\hat{\mathbf j}\\[4pt] &=9914.26\,\hat{\mathbf i}−100.7424\,\hat{\mathbf j} \end{align*}\]
Therefore, the ball hits the water about 9914.26 ft away from the base of the cliff. Notice that the vertical component of the position vector is very close to −100, which tells us that the ball just hit the water. Note that 9914.26 feet is not the true range of the cannon since the cannonball lands in the ocean at a location below the cannon. The range of the cannon would be determined by finding how far out the cannonball is when its height is 100 ft above the water (the same as the altitude of the cannon).
An archer fires an arrow at an angle of 40° above the horizontal with an initial speed of 98 m/sec. The height of the archer is 171.5 cm. Find the horizontal distance the arrow travels before it hits the ground.
- Hint
-
The equation for the position vector needs to account for the height of the archer in meters.
- Answer
-
967.15 m
One final question remains: In general, what is the maximum distance a projectile can travel, given its initial speed? To determine this distance, we assume the projectile is fired from ground level and we wish it to return to ground level. In other words, we want to determine an equation for the range. In this case, the equation of projectile motion is
\[\vecs{s}=v_0 t \cos\theta \,\hat{\mathbf i} + \left(v_0t\sin\theta - \dfrac{1}{2}gt^2 \right)\,\hat{\mathbf j}. \nonumber \]
Setting the second component equal to zero and solving for \(t\) yields
\[\begin{align*} v_0 t \sin\theta - \dfrac{1}{2}gt^2 =0\\ t\left(v_0 \sin\theta - \dfrac{1}{2}gt\right) =0 \end{align*}\]
Therefore, either \(t=0\) or \(t=\dfrac{2v_0\sin\theta}{g}\). We are interested in the second value of \(t\), so we substitute this into \(\vecs{s}(t)\), which gives
\[\begin{align*} \vecs{s}\left(\dfrac{2v_0\sin\theta}{g} \right) = v_0 \left(\dfrac{2v_0\sin\theta}{g} \right) \cos\theta \,\hat{\mathbf i} + \left( v_0\left(\dfrac{2v_0\sin\theta}{g} \right)\sin\theta - \dfrac{1}{2}g\left(\dfrac{2v_0\sin\theta}{g} \right)^2 \right)\,\hat{\mathbf j} \\ = \left(\dfrac{2v_0^2\sin\theta\cos\theta}{g} \right)\,\hat{\mathbf i} \\ = \dfrac{v_0^2 \sin2\theta}{g}\,\hat{\mathbf i}. \end{align*}\]
Thus, the expression for the range of a projectile fired at an angle \(\theta\) is
\[R=\dfrac{v_0^2 \sin2\theta}{g}\,\hat{\mathbf i} . \nonumber \]
The only variable in this expression is \( \theta\). To maximize the distance traveled, take the derivative of the coefficient of \( \hat{\mathbf i} \) with respect to \(\theta\) and set it equal to zero:
\[\begin{align*} \dfrac{d}{d\theta} \left( \dfrac{v_0^2 \sin2\theta}{g} \right) =0\\ \dfrac{2v_0^2\cos2\theta}{g} =0\\ \theta=45^\circ \end{align*}\]
This value of \(\theta)\) is the smallest positive value that makes the derivative equal to zero. Therefore, in the absence of air resistance, the best angle to fire a projectile (to maximize the range) is at a 45° angle. The distance it travels is given by
\[\vecs{s}\left(\dfrac{2v_0 \sin 45^\circ}{g} \right)= \dfrac{v_0^2 \sin 90^\circ}{g} \,\hat{\mathbf i} = \dfrac{v_0^2}{g}\,\hat{\mathbf i} \nonumber \]
Therefore, the range for an angle of 45° is \(\dfrac{v_0^2}{g}\) units.
Kepler’s Laws
During the early 1600s, Johannes Kepler was able to use the amazingly accurate data from his mentor Tycho Brahe to formulate his three laws of planetary motion, now known as Kepler’s laws of planetary motion. These laws also apply to other objects in the solar system in orbit around the Sun, such as comets (e.g., Halley’s comet) and asteroids. Variations of these laws apply to satellites in orbit around Earth.
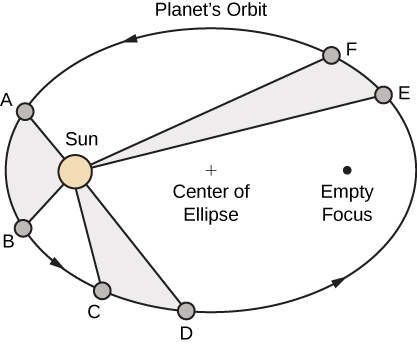
- The path of any planet about the Sun is elliptical in shape, with the center of the Sun located at one focus of the ellipse (the law of ellipses).
- A line drawn from the center of the Sun to the center of a planet sweeps out equal areas in equal time intervals (the law of equal areas) (Figure \(\PageIndex{8}\)).
- The ratio of the squares of the periods of any two planets is equal to the ratio of the cubes of the lengths of their semimajor orbital axes (the Law of Harmonies).
Kepler’s third law is especially useful when using appropriate units. In particular, 1 astronomical unit is defined to be the average distance from Earth to the Sun, and is now recognized to be 149,597,870,700 m or, approximately 93,000,000 mi. We therefore write 1 A.U. = 93,000,000 mi. Since the time it takes for Earth to orbit the Sun is 1 year, we use Earth years for units of time. Then, substituting 1 year for the period of Earth and 1 A.U. for the average distance to the Sun, Kepler’s third law can be written as
\[ T_p^2=D_p^3 \nonumber \]
for any planet in the solar system, where \(T_P\) is the period of that planet measured in Earth years and \(D_P\) is the average distance from that planet to the Sun measured in astronomical units. Therefore, if we know the average distance from a planet to the Sun (in astronomical units), we can then calculate the length of its year (in Earth years), and vice versa.
Kepler’s laws were formulated based on observations from Brahe; however, they were not proved formally until Sir Isaac Newton was able to apply calculus. Furthermore, Newton was able to generalize Kepler’s third law to other orbital systems, such as a moon orbiting around a planet. Kepler’s original third law only applies to objects orbiting the Sun.
Let’s now prove Kepler’s first law using the calculus of vector-valued functions. First we need a coordinate system. Let’s place the Sun at the origin of the coordinate system and let the vector-valued function \(\vecs{r}(t)\) represent the location of a planet as a function of time. Newton proved Kepler’s law using his second law of motion and his law of universal gravitation. Newton’s second law of motion can be written as \(\vecs{F}=m\vecs{a}\), where \(\vecs{F}\) represents the net force acting on the planet. His law of universal gravitation can be written in the form \(\vecs{F}=−\dfrac{GmM}{||\vecs{r}||^2}\cdot \dfrac{\vecs{r}}{||\vecs{r} ||}\), which indicates that the force resulting from the gravitational attraction of the Sun points back toward the Sun, and has magnitude \(\dfrac{GmM}{||\vecs{r}||^2} \) (Figure \(\PageIndex{9}\)).
Setting these two forces equal to each other, and using the fact that \(\vecs a(t)=\vecs v^{\,\prime}(t)\), we obtain
\[ m\vecs v^{\,\prime}(t)=−\frac{GmM}{‖\vecs r‖^2}⋅\frac{\vecs r}{‖\vecs r‖}, \nonumber \]
which can be rewritten as
\[ \dfrac{d\vecs v}{dt}=−\dfrac{GM}{||\vecs r||^3}\vecs{r}. \nonumber \]
This equation shows that the vectors \(d\vecs{v}/dt\) and \(\vecs r\) are parallel to each other, so \(d\vecs {v}/dt \times \vecs {r}=\vecs 0\). Next, let’s differentiate \(\vecs{r} \times \vecs{v}\) with respect to time:
\[\dfrac{d}{dt}(\vecs{r}\times \vecs{v})=\dfrac{d\vecs{r}}{dt}\times \vecs v+\vecs{r} \times \dfrac{d\vecs{v}}{dt}=\vecs{v}\times \vecs{v}+\vecs{0}=\vecs{0}. \label{Eq10} \]
This proves that \(\vecs{r}\times\vecs{v}\) is a constant vector, which we call \(\vecs C\). Since \(\vecs r\) and \(\vecs v\) are both perpendicular to \(\vecs C\) for all values of \(t\), they must lie in a plane perpendicular to \(\vecs C\). Therefore, the motion of the planet lies in a plane.
Next we calculate the expression \(d\vecs{v}/dt\times \vecs C\):
\[\dfrac{d\vecs{v}}{dt} \times \vecs{C}=−\dfrac{GM}{||\vecs{r}||^3}\vecs{r}\times (\vecs{r}\times\vecs{v})=−\dfrac{GM}{||\vecs r||^3}[(\vecs{r} \cdot \vecs{v})\vecs{r} - (\vecs{r} \cdot \vecs{r})\vecs{v}]. \label{Eq11} \]
The last equality in Equation \ref{Eq11} is from the triple cross product formula (see the cross product section in Introduction to Vectors in Space). We need an expression for \(\vecs{r}\cdot \vecs{v}\). To calculate this, we differentiate \(\vecs{r}\cdot \vecs{r}\) with respect to time:
\[ \dfrac{d}{dt}(\vecs{r}\cdot \vecs{r})=\dfrac{d\vecs{r}}{dt}\cdot \vecs{r}+\vecs{r}\cdot \dfrac{d\vecs{r}}{dt}=2\vecs{r}\cdot \dfrac{d\vecs{r}}{dt}=2\vecs{r}\cdot \vecs{v}. \label{Eq12} \]
Since \(\vecs{r}\cdot\vecs{r}=||\vecs r||^2\), we also have
\[\dfrac{d}{dt}(\vecs{r}\cdot \vecs{r})=\dfrac{d}{dt}||\vecs{r}||^2=2||\vecs{r}|| \dfrac{d}{dt}||\vecs{r}||. \label{Eq13} \]
Combining Equation \ref{Eq12} and Equation \ref{Eq13}, we get
\[\begin{align*} 2\vecs{r}\cdot \vecs{v} =2||\vecs{r}||\dfrac{d}{dt}||\vecs{r}|| \\ \vecs{r} \cdot \vecs{v} =||\vecs{r}‖\dfrac{d}{dt}||\vecs{r}||. \end{align*} \label{Eq14} \]
Substituting this into Equation \ref{Eq11} gives us
\[\begin{align} \dfrac{d\vecs{v}}{dt} \times \vecs{C} = - \dfrac{GM}{||\vecs{r}||^3} [(\vecs{r}\cdot \vecs{v})\vecs{r} - (\vecs{r}\cdot \vecs{r})\vecs{v}] \nonumber \\ = -\dfrac{GM}{||\vecs{r}||^3}\left[ ||\vecs{r} \left(\dfrac{d}{dt} ||\vecs{r}||\right)\vecs{r} - ||\vecs{r}||^2\vecs{v} \right] \nonumber \\ = -GM\left[ \dfrac{1}{||\vecs{r}||^2}\left( \dfrac{d}{dt} ||\vecs{r}|| \right)\vecs{r} - \dfrac{1}{||\vecs{r}||}\vecs{v} \right] \nonumber \\ = GM\left[ \dfrac{\vecs{v}}{||\vecs{r}||} -\dfrac{\vecs{r}}{||\vecs{r}||^2}\left( \dfrac{d}{dt} ||\vecs{r}|| \right) \right]. \label{Eq15} \end{align} \]
However,
\[ \begin{align*} \dfrac{d}{dt} \dfrac{\vecs{r}}{||\vecs{r}||} = \dfrac{ \frac{d}{dt}(\vecs{r})||\vecs{r}||- \vecs{r}\frac{d}{dt}||\vecs{r}|| }{||\vecs{r}||^2} \\ = \dfrac{ \frac{d\vecs{r}}{dt} }{||\vecs{r}||} - \dfrac{\vecs{r}}{||\vecs{r}||^2}\dfrac{d}{dt}||\vecs{r} || \\ = \dfrac{\vecs{v}}{||\vecs{r}||} - \dfrac{\vecs{r}}{||\vecs{r}||^2} \dfrac{d}{dt}||\vecs{r}||. \end{align*}\]
Therefore, Equation \ref{Eq15} becomes
\[\dfrac{d \vecs{v}}{dt}\times \vecs{C}=GM\left( \dfrac{d}{dt}\dfrac{ \vecs{r}}{ || \vecs{r} ||} \right).\nonumber \]
Since \(\vecs{C}\) is a constant vector, we can integrate both sides and obtain
\[ \vecs{v}\times\vecs{C} = GM \dfrac{ \vecs{r} }{|| \vecs{r} ||} + \vecs{D}, \nonumber \]
where \(\vecs D\) is a constant vector. Our goal is to solve for \(|| \vecs{r} ||\). Let’s start by calculating \( \vecs{r} \cdot ( \vecs{v}\times \vecs{C}\):
\[\vecs{r} \cdot ( \vecs{v}\times \vecs{C} =GM\dfrac{||\vecs{r}||^2}{||\vecs{r}||}+ \vecs{r}\cdot\vecs{D} =GM||\vecs{r}||+\vecs{r}\cdot \vecs{D}. \nonumber \]
However, \( \vecs{r} \cdot ( \vecs{v}\times \vecs{C})= ( \vecs{r} \times \vecs{v})\cdot \vecs{C} \), so
\[ ( \vecs{r} \times \vecs{v})\cdot \vecs{C} =GM||\vecs{r}|| + \vecs{r}\cdot \vecs{D}.\nonumber \]
Since \(\vecs{r}\times \vecs{v}=\vecs{C}\), we have
\[ ||\vecs{C}||^2 =GM||\vecs{r}|| +\vecs{r}\cdot \vecs{D}.\nonumber \]
Note that \( \vecs{r} \cdot \vecs{D}=||\vecs{r}|| ||\vecs{D}||\cos \theta \), where \(\theta\) is the angle between \(\vecs{r}\) and \(\vecs{D}\). Therefore,
\[ ||\vecs{C}||^2=GM||\vecs{r}||+||\vecs{r}|| ||\vecs{D}|| \cos\theta \nonumber \]
Solving for \(||\vecs{r}||\),
\[ ||\vecs{r}|| = \dfrac{||\vecs{C}||^2 }{GM+||\vecs{D}||\cos\theta} = \dfrac{||\vecs{C}||^2}{GM}\left( \dfrac{1}{1+e\cos\theta} \right). \nonumber \]
where \(e=||\vecs{D}||/GM\). This is the polar equation of a conic with a focus at the origin, which we set up to be the Sun. It is a hyperbola if \(e>1\), a parabola if \(e=1\), or an ellipse if \(e<1\). Since planets have closed orbits, the only possibility is an ellipse. However, at this point it should be mentioned that hyperbolic comets do exist. These are objects that are merely passing through the solar system at speeds too great to be trapped into orbit around the Sun. As they pass close enough to the Sun, the gravitational field of the Sun deflects the trajectory enough so the path becomes hyperbolic.
\(\square\)
Kepler’s third law of planetary motion can be modified to the case of one object in orbit around an object other than the Sun, such as the Moon around the Earth. In this case, Kepler’s third law becomes
\[P^2 = \dfrac{4\pi^2 a^3}{G(m+M)}, \label{Eq30} \]
where m is the mass of the Moon and M is the mass of Earth, a represents the length of the major axis of the elliptical orbit, and P represents the period.
Given that the mass of the Moon is \(7.35\times 10^{22}\) kg, the mass of Earth is \(5.97\times 10^{24}\) kg, \(G=6.67\times 10^{−11} \text{m} / \text{kg} \cdot \text{sec}^2\), and the period of the moon is 27.3 days, let’s find the length of the major axis of the orbit of the Moon around Earth.
Solution
It is important to be consistent with units. Since the universal gravitational constant contains seconds in the units, we need to use seconds for the period of the Moon as well:
\[27.3 \; \text{days} \times \dfrac{24 \; \text{hr}}{1 \; \text{day}} \times \dfrac{3600 \; \text{esc}}{1 \; \text{hour}} =2,358,720\; \text{sec}\nonumber \]
Substitute all the data into Equation \ref{Eq30} and solve for \(a\):
\[\begin{align*} (2,358,720sec)^2 = \dfrac{4\pi^2a^3}{\left( 6.67\times 10^{-11} \frac{m}{\text{kg}\times \text{sec}^2}\right) (7.35\times 10^{22}\text{kg} + 5.97 \times 10^{24}\text{kg})} \\ 5.563 \times 10^{12} = \dfrac{ 4\pi^2a^3}{(6.67 \times 10^{-11}\text{m}^3)(6.04 \times 10^{24})} \\ (5.563 \times 10^{12})(6.67 \times 10^{-11} \text{m}^3)(6.04 \times 10^{24}) = 4\pi^2 a^3 \\ a^3 = \dfrac{2.241 \times 10^{27}}{4\pi^2}\text{m}^3 \\ a = 3.84 \times 10^8 \text{m} \\ \approx 384,000 \,\text{km}. \end{align*}\]
Analysis
According to solarsystem.nasa.gov, the actual average distance from the Moon to Earth is 384,400 km. This is calculated using reflectors left on the Moon by Apollo astronauts back in the 1960s.
Titan is the largest moon of Saturn. The mass of Titan is approximately \(1.35 \times 10^{23} kg\). The mass of Saturn is approximately \( 5.68 \times 10^{26}\) kg. Titan takes approximately 16 days to orbit Saturn. Use this information, along with the universal gravitation constant \(G=6.67×10^{−11} \text{m}/\text{kg} \cdot \text{sec}^2\) to estimate the distance from Titan to Saturn.
- Hint
-
Make sure your units agree, then use Equation \ref{Eq30}.
- Answer
-
\[a\approx 1.224 \times 10^9 \text{m}= 1,224,000 \text{km} \nonumber \]
We now return to the chapter opener, which discusses the motion of Halley’s comet around the Sun. Kepler’s first law states that Halley’s comet follows an elliptical path around the Sun, with the Sun as one focus of the ellipse. The period of Halley’s comet is approximately 76.1 years, depending on how closely it passes by Jupiter and Saturn as it passes through the outer solar system. Let’s use \(T=76.1\) years. What is the average distance of Halley’s comet from the Sun?

Solution
Using the equation \(T^2=D^3\) with \(T=76.1\), we obtain \(D^3=5791.21\), so \(D\approx 17.96\) A.U. This comes out to approximately \(1.67\times 10^9\) mi.
A natural question to ask is: What are the maximum (aphelion) and minimum (perihelion) distances from Halley’s Comet to the Sun? The eccentricity of the orbit of Halley’s Comet is 0.967 (Source: http://nssdc.gsfc.nasa.gov/planetary...cometfact.html). Recall that the formula for the eccentricity of an ellipse is \(e=c/a\), where a is the length of the semimajor axis and c is the distance from the center to either focus. Therefore, \(0.967=c/17.96\) and \(c\approx 17.37\) A.U. Subtracting this from a gives the perihelion distance \(p=a−c=17.96−17.37=0.59\) A.U. According to the National Space Science Data Center (Source: http://nssdc.gsfc.nasa.gov/planetary...cometfact.html), the perihelion distance for Halley’s comet is 0.587 A.U. To calculate the aphelion distance, we add
\[ P=a+c=17.96+17.37=35.33 \; \text{A.U.} \nonumber \]
This is approximately \(3.3\times 10^9\) mi. The average distance from Pluto to the Sun is 39.5 A.U. (Source: http://www.oarval.org/furthest.htm), so it would appear that Halley’s Comet stays just within the orbit of Pluto.
How fast can a racecar travel through a circular turn without skidding and hitting the wall? The answer could depend on several factors:
- The weight of the car;
- The friction between the tires and the road;
- The radius of the circle;
- The “steepness” of the turn.
In this project we investigate this question for NASCAR racecars at the Bristol Motor Speedway in Tennessee. Before considering this track in particular, we use vector functions to develop the mathematics and physics necessary for answering questions such as this.
A car of mass \(m\) moves with constant angular speed \(\omega\) around a circular curve of radius \(R\) (Figure \(\PageIndex{9}\)). The curve is banked at an angle \(\theta\). If the height of the car off the ground is \(h\), then the position of the car at time \(t\) is given by the function \(\vecs r(t)=< R\cos(\omega t),R\sin(\omega t),h>\).

- Find the velocity function \(\vecs{v}(t)\) of the car. Show that \(\vecs{v}\) is tangent to the circular curve. This means that, without a force to keep the car on the curve, the car will shoot off of it.
- Show that the speed of the car is \(\omega R\). Use this to show that \((2\pi 4)/\|\vecs{v}\|=(2\pi)/\omega \).
- Find the acceleration \(\vecs{a}\). Show that this vector points toward the center of the circle and that \(\|\vecs{a}\|=R\omega ^2\).
- The force required to produce this circular motion is called the centripetal force, and it is denoted \( \vecs{F}_{cent} \). This force points toward the center of the circle (not toward the ground). Show that \(\|\vecs{F}_{cent}\|=\left(m|\vecs{v}|^2 \right)/R\).
As the car moves around the curve, three forces act on it: gravity, the force exerted by the road (this force is perpendicular to the ground), and the friction force (Figure \(\PageIndex{10}\)). Because describing the frictional force generated by the tires and the road is complex, we use a standard approximation for the frictional force. Assume that \(\vecs{f}=\mu \vecs{N}\) for some positive constant \(\mu \). The constant \(\mu\) is called the coefficient of friction.
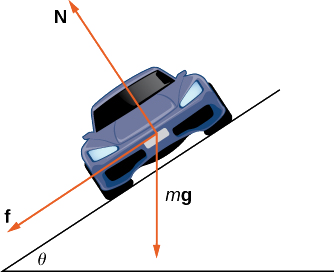
Let \(v_{max}\) denote the maximum speed the car can attain through the curve without skidding. In other words, \(v_{max}\) is the fastest speed at which the car can navigate the turn. When the car is traveling at this speed, the magnitude of the centripetal force is
\[\| \vecs{F}_{cent} \| = \dfrac{m(v_{max})^2}{R}. \nonumber \]
The next three questions deal with developing a formula that relates the speed \(v_{max}\) to the banking angle \(\theta\).
- Show that \(\vecs{N} \cos\theta=m\vecs g+\vecs{f} \sin\theta\). Conclude that \(\vecs{N}=(m\vecs g)/(\cos\theta−\mu \sin\theta)\).
- The centripetal force is the sum of the forces in the horizontal direction, since the centripetal force points toward the center of the circular curve. Show that
\[\vecs{F}_{cent}=\vecs{N} \sin\theta+\vecs{f}\cos\theta. \nonumber \]
Conclude that\[\vecs{F}_{cent}=\dfrac{\sin\theta+\mu \cos\theta}{cos\theta−\mu \sin\theta} m\vecs g. \nonumber \]
- Show that \((v_{\text{max}})^2=((\sin\theta+\mu\ cos\theta)/(\cos\theta−\mu \sin\theta))gR\). Conclude that the maximum speed does not actually depend on the mass of the car.
Now that we have a formula relating the maximum speed of the car and the banking angle, we are in a position to answer the questions like the one posed at the beginning of the project.
The Bristol Motor Speedway is a NASCAR short track in Bristol, Tennessee. The track has the approximate shape shown in Figure \(\PageIndex{11}\). Each end of the track is approximately semicircular, so when cars make turns they are traveling along an approximately circular curve. If a car takes the inside track and speeds along the bottom of turn 1, the car travels along a semicircle of radius approximately 211 ft with a banking angle of 24°. If the car decides to take the outside track and speeds along the top of turn 1, then the car travels along a semicircle with a banking angle of 28°. (The track has variable angle banking.)

The coefficient of friction for a normal tire in dry conditions is approximately 0.7. Therefore, we assume the coefficient for a NASCAR tire in dry conditions is approximately 0.98.
Before answering the following questions, note that it is easier to do computations in terms of feet and seconds, and then convert the answers to miles per hour as a final step.
- In dry conditions, how fast can the car travel through the bottom of the turn without skidding?
- In dry conditions, how fast can the car travel through the top of the turn without skidding?
- In wet conditions, the coefficient of friction can become as low as 0.1. If this is the case, how fast can the car travel through the bottom of the turn without skidding?
- Suppose the measured speed of a car going along the outside edge of the turn is 105 mph. Estimate the coefficient of friction for the car’s tires.
Key Concepts
- If \(\vecs{r}(t)\) represents the position of an object at time t, then \(\vecs{r}^{\,\prime}(t)\) represents the velocity and \(\vecs{r}′^{\,\prime}(t)\) represents the acceleration of the object at time t. The magnitude of the velocity vector is speed.
- The acceleration vector always points toward the concave side of the curve defined by \(\vecs{r}(t)\). The tangential and normal components of acceleration \(a_\vecs{T}\) and \(a_\vecs{N}\) are the projections of the acceleration vector onto the unit tangent and unit normal vectors to the curve.
- Kepler’s three laws of planetary motion describe the motion of objects in orbit around the Sun. His third law can be modified to describe motion of objects in orbit around other celestial objects as well.
- Newton was able to use his law of universal gravitation in conjunction with his second law of motion and calculus to prove Kepler’s three laws.
Key Equations
- Velocity \[\vecs{v}(t)=\vecs{r}^{\,\prime}(t) \nonumber \]
- Acceleration \[\vecs{a}(t)=\vecs{v}^{\,\prime}(t)=\vecs{r}′^{\,\prime}(t) \nonumber \]
- Speed \[v(t)=||\vecs{v}(t)||=||\vecs{r}^{\,\prime}(t)||=\dfrac{ds}{dt} \nonumber \]
- Tangential component of acceleration \[a_{\vecs{T}} =\vecs{a}\cdot \vecs{T}=\dfrac{\vecs{v}\cdot \vecs{a}}{||\vecs v||} \nonumber \]
- Normal component of acceleration \[a_{\vecs{N}}=\vecs{a}\cdot \vecs{N} = \dfrac{|| \vecs{v} \times \vecs{a} ||}{||\vecs{v}||} = \sqrt{||\vecs{a}||^2 - a_{\vecs{T}}} \nonumber \]
Glossary
- acceleration vector
- the second derivative of the position vector
- Kepler’s laws of planetary motion
- three laws governing the motion of planets, asteroids, and comets in orbit around the Sun
- normal component of acceleration
- the coefficient of the unit normal vector \(\vecs N\) when the acceleration vector is written as a linear combination of \(\vecs T\) and \(\vecs N\)
- projectile motion
- motion of an object with an initial velocity but no force acting on it other than gravity
- tangential component of acceleration
- the coefficient of the unit tangent vector \(\vecs T\) when the acceleration vector is written as a linear combination of \(\vecs T\) and \(\vecs N\)
- velocity vector
- the derivative of the position vector
Contributors and Attributions
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.
- Edited by Paul Seeburger
Paul Seeburger added finding point \((1, 2)\) when \(t=1\) in Example \(\PageIndex{1}\).
He also created Figure \(\PageIndex{1}\).

