4.9: Hyperbolic Functions
- Page ID
- 525
Definition of the Hyperbolic Functions
We define the hyperbolic functions as follows:
\[ \sinh x = \dfrac{e^x - e^{-x}}{2}, \]
\[ \cosh x = \dfrac{e^x + e^{-x}}{2},\]
\[ \tanh x = \dfrac{\sinh x}{\cosh x}.\]
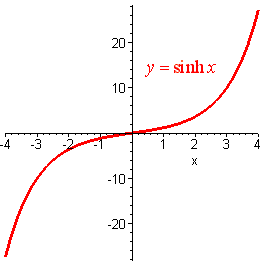
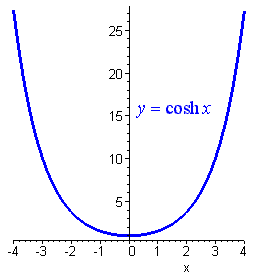
Properties of Hyperbolic Functions
- \( \cosh^2 x - \sinh^2 x = 1 \),
- \( \dfrac{d}{dx} \sinh x = \cosh x\),
- \(\dfrac{d}{dx} \cosh x = \sinh x\).
Proof of Property A
We find
\[\begin{align*} \cosh^2 x - \sinh^2 x &= \left( \dfrac{e^x+e^{-x}}{2} \right)^2 - \left( \dfrac{e^x-e^{-x}}{2} \right)^2 \\[4pt] &= \dfrac{e^{2x}+2+e^{-2x}}{4} - \dfrac{e^{2x}-2+e^{-2x}}{4} \\[4pt] &= \dfrac{4}{4} =1. \end{align*} \]
\(\square\)
The Derivative of the Inverse Hyperbolic Trig Functions
\[ \dfrac{d}{dx} \sinh^{-1} x = \dfrac{1}{\sqrt{1+x^2}},\]
\[ \dfrac{d}{dx} \cosh^{-1} x = \dfrac{1}{\sqrt{x^2-1}},\]
\[ \dfrac{d}{dx} \tanh^{-1} x = \dfrac{d}{dx} \coth^{-1} x = \dfrac{1}{1-x^2},\]
\[ \dfrac{d}{dx} \text{sech}^{-1} x = \dfrac{1}{x\sqrt{1-x^2}},\]
\[ \dfrac{d}{dx} \text{csch}^{-1} x = \dfrac{1}{x\sqrt{1+x^2}}.\]
Proof of the third identity
We have
\[ \tanh (\tanh^{-1} x) = x. \nonumber\]
Taking derivatives implicitly, we have
\[ \dfrac{d}{dx} \text{sech}^2 (\tanh^{-1} x = \tanh^{-1} x = 1. \nonumber\]
Dividing gives
\[ \dfrac{d}{dx} \tanh^{-1} x = \dfrac{1}{\text{sech}^2 (\tan^{-1} x)}. \nonumber\]
Since
\[ \cosh^2(x) - \sinh^2(x) = 1, \nonumber\]
dividing by \(\cosh^2(x)\), we get
\[1 - \tanh^2(x) = \text{sech}^2(x) \nonumber\]
so that
\[\begin{align*} \dfrac{d}{dx} \tan^{-1} x &= \dfrac{1}{1-\tanh^2 (\tanh^{-1} x)} \\[4pt] &= \dfrac{1}{1-x^2}. \end{align*}
\(\square\)
For the derivative of the \(\text{sech}^{-1} (x)\) click here.
Integration and Hyperbolic Functions
Now we are ready to use the arc hyperbolic functions for integration.
Example \(\PageIndex{1}\)
Evaluate
\[ \int \dfrac{dx}{4-x^2} \nonumber\]
Solution
\[ \int \dfrac{dx}{4-x^2} = \int \dfrac{1}{4} \int \dfrac{dx}{1-(2/3)^2}\nonumber\]
let \( u = \dfrac{x}{2}\), then \(du = \dfrac{1}{2}dx\)
\[ \dfrac{1}{2} \int \dfrac{du}{1-u^2}= \dfrac{1}{2}\tanh^{-1} u +C = \dfrac{1}{2} \tanh^{-1} \left(\dfrac{x}{2}\right) + C.\nonumber\]
Example \(\PageIndex{2}\)
Evaluate
\[ \int \dfrac{x}{1-x^4} dx. \nonumber\]
Solution
Although this is not directly a derivative of a hyperbolic trig function, we can use the substitution \( u = x^2 \) and \(du = 2x\, dx\).
To change the integral to
\[\begin{align*} \dfrac{1}{2} \int \dfrac{du}{1-u^2} &= \dfrac{1}{2} \tanh^{-1} u + C \\[4pt] &= \dfrac{1}{2} \tanh^{-1} (x^2) + C. \end{align*}\]
Contributors and Attributions
- Larry Green (Lake Tahoe Community College)
Integrated by Justin Marshall.


