4.3: Line Integrals
- Page ID
- 567
In this section we are going to cover the integration of a line over a 3-D scalar field. When you learned on dimensional integrals, we integrated functions of \(y\) with respect to \(x\) and assumed that \(z\), the third dimension, does not change. If, however, the third dimension does change, the line is not linear and there is there is no way to integrate with respect to one variable. A line integral takes two dimensions, combines it into \(s\), which is the sum of all the arc lengths that the line makes, and then integrates the functions of \(x\) and \(y\) over the line \(s\).
Definition of a Line Integral
By this time you should be used to the construction of an integral. We break a geometrical figure into tiny pieces, multiply the size of the piece by the function value on that piece and add up all the products. For one variable integration the geometrical figure is a line segment, for double integration the figure is a region, and for triple integration the figure is a solid.
The geometrical figure of the day will be a curve. If we have a function defined on a curve we can break up the curve into tiny line segments, multiply the length of the line segments by the function value on the segment and add up all the products. As always, we will take a limit as the length of the line segments approaches zero. This new quantity is called the line integral and can be defined in two, three, or higher dimensions.
Suppose that a wire has as density \(f(x,y,z)\) at the point \((x,y,z)\) on the wire. Then the line integral will equal the total mass of the wire. Below is the definition in symbols.
Definition: Line Integrals
Let \(f\) be a function defined on a curve \(C\) of finite length. Then the line integral of \(f\) along \(C\) is
\[\int_C \; f(x,y) ds= \lim_{n \rightarrow \infty} \sum_{i=1}^{n} f(x_i,y_i)\Delta s_i\nonumber \]
(for two dimensions)
\[\int_C \; f(x,y,z) ds= \lim_{n \rightarrow \infty} \sum_{i=1}^{n} f(x_i,y_i,z_i)\Delta s_i\nonumber \]
(for three dimensions)
A scalar field has a value associated to each point in space. Examples of scalar fields are height, temperature or pressure maps. In a two-dimensional field, the value at each point can be thought of as a height of a surface embedded in three dimensions. The line integral of a curve along this scalar field is equivalent to the area under a curve traced over the surface defined by the field.
| requirement | simple integrals | For line integrals |
|---|---|---|
| 1 | an equation of the function \(f(x)\) AKA \(y=\) | an equation of the function \(f(x,y)\) AKA \(z=\) |
| 2 | the equation of the path in parametric form \(( x(t),y(t) )\) | |
| 3 | bounds in terms of \(x=a\) and \(x=b\) | the bounds in terms of \(t=a\) and \(t=b\) |
The length of the line can be determined by the sum of its arclengths
\[\lim_{n \to \infty }\sum_{i=1}^{n}\Delta_i =\int _a^b d(s)=\int_a^b\sqrt {\left ( \dfrac{dx}{dt} \right )^2+\left ( \dfrac{dy}{dt} \right )^2}dt\nonumber \]
note that the arc length can also be determined using the vector components \( s(t)=x(t)i+y(t)j+z(t)k \)
\[ds= \left | \dfrac{ds}{dt} \right|=\sqrt {\left ( \dfrac{dx}{dt} \right )^2+\left ( \dfrac{dy}{dt} \right )^2+\left ( \dfrac{dz}{dt} \right )^2} dt =\left |\dfrac{dr}{dt}\right | dt\nonumber \]
so a line integral is sum of arclength multiplied by the value at that point
\[\lim_{n\rightarrow \infty}\sum_{i=1}^{n}f(c_i)\Delta s_i=\int_a^b f(x,y)ds=\int_a^b f(x(t),y(t))\sqrt {\left ( \dfrac{dx}{dt} \right )^2+\left ( \dfrac{dy}{dt} \right )^2}dt\nonumber \]
where \(c_i\) are partitions from \(a\) to \(b\) spaced by \(ds_i\). Here is a visual representation of a line integral over a scalar field.
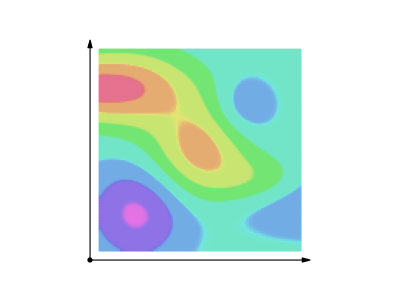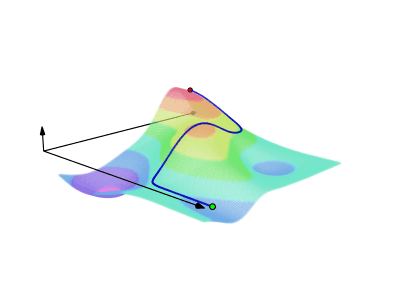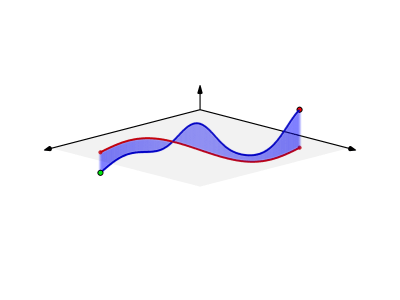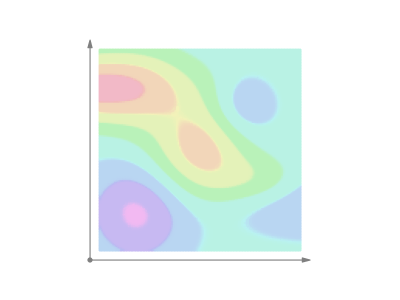
All these processes are represented step-by-step, directly linking the concept of the line integral over a scalar field to the representation of integrals, as the area under a simpler curve. A breakdown of the steps:
- The color-coded scalar field \(f\) and a curve \(C\) are shown. The curve \(C \) starts at \(a\) and ends at \(b\).
- The field is rotated in 3D to illustrate how the scalar field describes a surface. The curve \(C\), in blue, is now shown along this surface. This shows how at each point in the curve, a scalar value (the height) can be associated.
- The curve is projected onto the plane \(XY\) (in gray), giving us the red curve, which is exactly the curve \(C\) as seen from above in the beginning. This is red curve is the curve in which the line integral is performed. The distances from the projected curve (red) to the curve along the surface (blue) describes a "curtain" surface (in blue).
- The graph is rotated to face the curve from a better angle
- The projected curve is rectified (made straight), and the same transformation follows on the blue curve, along the surface. This shows how the line integral is applied to the arc length of the given curve.
- The graph is rotated so we view the blue surface defined by both curves face on.
- This final view illustrates the line integral as the familiar integral of a function, whose value is the "signed area" between the X axis (the red curve, now a straight line) and the blue curve (which gives the value of the scalar field at each point). Thus, we conclude that the two integrals are the same, illustrating the concept of a line integral on a scalar field in an intuitive way.
Evaluating Line Integrals
This definition is not very useful by itself for finding exact line integrals. If data is provided, then we can use it as a guide for an approximate answer. Fortunately, there is an easier way to find the line integral when the curve is given parametrically or as a vector valued function. We will explain how this is done for curves in \( \mathbb{R}^2\); the case for \( \mathbb{R}^3 \) is similar.
Let
\[ \textbf{r}(t) = x(t) \hat{\textbf{i}} + y(t) \hat{\textbf{j}} \nonumber \]
be a differentiable vector valued function. Then
\[ds = ||r'(t)||\; dt = \sqrt{(x'(t))^2+(y'(t))^2}. \nonumber \]
We are now ready to state the theorem that shows us how to compute a line integral.
Theorem: Line Integrals of Vector Valued Functions
Let
\[\textbf{r}(t) = x(t) \hat{\textbf{i}} + y(t) \hat{\textbf{j}} \; \; \; \; a \leq t \leq b \nonumber \]
be a differentiable vector valued function that defines a smooth curve \(C\). Then
\[\int_C \; f(x,y) \; ds= \int_a^b f(x(t),y(t)) \sqrt{(x'(t))^2+(y'(t))^2} \; dt \nonumber \]
and for three dimensions, if
\[\textbf{r}(t)= x(t) \hat{\textbf{i}} + y(t) \hat{\textbf{j}} + z(t) \hat{\textbf{k}} \;\;\;\; a \leq t \leq b\nonumber \]
then
\[\int_C \; f(x,y) \; ds= \int_a^b f(x(t),y(t),z(t))\ \sqrt{(x'(t))^2+(y'(t))^2+(z'(t)^2)} \; dt . \nonumber \]
Example \(\PageIndex{1}\)
Find the line integral
\[ \int_c (1+ x^2y) ds \nonumber \nonumber \]
where \(C\) is the ellipse
\[r(t) = (2\cos \,t) \hat{\textbf{i}} + (3\sin\, t) \hat{\textbf{j}} \nonumber \nonumber \]
for \( 0 \le t \le 2\pi\).
You may use a calculator or computer to evaluate the final integral.
Solution
We find
\[ds = \sqrt{(-2 \sin t) + (3 \cos t)^2} \; dt = \sqrt{4 \sin^2 t + 9 \cos^2 t}\; dt . \nonumber\nonumber \]
We have the integral
\[\int_0^{2\pi} (1+(2 \cos t)^2)(3 \sin t ))\sqrt{4\sin^2 t + 9 \cos^2 t} \; dt. \nonumber \nonumber \]
With the help of a machine, we get 15.87.
Work
The main application of line integrals is finding the work done on an object in a force field. If an object is moving along a curve through a force field \(F\), then we can calculate the total work done by the force field by cutting the curve up into tiny pieces. The work done \(W\) along each piece will be approximately equal to
\[dW = \vec{F} \cdot T\vec{ds}.\nonumber \]
Now recall that
\[T = \dfrac{ r'(t) }{ ||r'(t)|| }\nonumber \]
and that
\[\vec{ds} = ||\vec{r}'(t)||dt.\nonumber \]
Hence
\[dW = \vec{F} \cdot \vec{r}'(t) dt.\nonumber \]
As usual, we add up all the small pieces of work and take the limit as the pieces get small to end up with an integral.
Definition: Work
Let \(F\) be a vector field and \(C\) be a curve defined by the vector valued function \(\textbf{r}\). Then the work done by \(F\) on an object moving along \(C\) is given by
\[\text{Work} = \int_C F \cdot dr = \int_a^b F(x(t),y(t), z(t)) \cdot \textbf{r}'(t) \; dt. \nonumber \]
Example \(\PageIndex{2}\): Work
Find the work done by the vector field
\[\vec{F}(x,y,z) = x \hat{\textbf{i}} + 3xy \hat{\textbf{j}} - (x + z) \hat{\textbf{k}} \nonumber\nonumber \]
on a particle moving along the line segment that goes from \((1,4,2)\) to \((0,5,1)\)
Solution
We first have to parameterize the curve. We have
\[\textbf{r}(t) = \langle1,4,2\rangle + [\langle0,5,1\rangle - \langle1,4,2\rangle ]t = \langle1-t,4+t, 2-t\rangle \nonumber\nonumber \]
and
\[ \textbf{r}'(t) = -\hat{\textbf{i}} + \hat{\textbf{j}} - \hat{\textbf{k}}. \nonumber \nonumber \]
Taking the dot product, we get
\[ \begin{align*} F \cdot \textbf{r}'(t) &= -x + 3xy + x + z \\ &= 3xy + z \\ &= 3(1-t)(4+t) + (2-t) \\ &= -3t^2 - 10t +14. \end{align*} \nonumber \]
Now we just integrate
\[\int_0^1 (-3t^2 -10t +14)\; dt = \big[-t^3 - 5t^2 + 14t \big]_0^1 = 8. \nonumber \nonumber \]
Notice that work done by a force field on an object moving along a curve depends on the direction that the object goes. In fact the opposite direction will produce the negative of the work done in the original direction. This is clear from the fact that everything is the same except the order which we write a and b.
Line Integrals in Differential Form
We can rewrite \(\textbf{r}'(t) \; dt \) as
\[ \dfrac{d\textbf{r}}{dt} dt = \left(\dfrac{dx}{dt} \hat{\textbf{i}} +\dfrac{dy}{dt} \hat{\textbf{j}} +\dfrac{dz}{dt} \hat{\textbf{k}} \right) dt\nonumber \]
\[= dx \hat{\textbf{i}} + dy \hat{\textbf{j}} + dz \hat{\textbf{k}}. \nonumber \]
So that if
\[\vec{ F} = M \hat{\textbf{i}} + N \hat{\textbf{j}} + P \hat{\textbf{k}} \nonumber \]
then
\[F \cdot \textbf{r}'(t) \; dt = M \; dx + N \; dy + P \; dz. \nonumber \]
This is called the differential form of the line integral.
Example \(\PageIndex{3}\)
Find
\[ \int_c y\, dx + z\, dy \nonumber \nonumber \]
where \(C\) is the part of the helix
\[ \textbf{r}(t) = \sin t \, \hat{\textbf{i}} + \cos t\, \hat{\textbf{j}} + t \, \hat{\textbf{k}} \nonumber \nonumber \]
from \( 0 \leq t \leq 2\pi \).
Solution
We have
\[\textbf{r}'(t) = \cos t \hat{\textbf{i}} - \sin t \hat{\textbf{j}} + \hat{\textbf{k}} \nonumber \nonumber \]
so that
\[y \; dx + z \; dz = (\cos^2 t - t\sin t ) dt). \nonumber \nonumber \]
This leads us to the integral
\[ \int_0^{2\pi} \left( \cos^2 t - t\, \sin t\right) \, dt \nonumber\nonumber \]
with a little bit of effort (using integration by parts) we solve this integral to get \( 3\pi \)
Example \(\PageIndex{4}\)
Integrate \( f(x,y,z)= -\sqrt{x^2+y^2} \; \) over \(s(t)=(a\: \cos(t))j+(a\, \sin(t))k \: \) with \( 0\leq t \leq 2\pi \).
Solution
First we separate the equation for the line into two parametric equations
\[x=0\; \; \; y=a\: \cos (t)\; \; \; z=a\: \sin (t). \nonumber\nonumber \]
Next we find \(ds\) (Note: if dealing with 3 variables we can take the arc length the same way as with two variables)
\[\sqrt {\left ( \dfrac{dx}{dt} \right )^2+\left ( \dfrac{dy}{dt} \right )^2+\left ( \dfrac{dz}{dt} \right )^2}dt \nonumber \nonumber \]
\[\sqrt {\left ( 0 \right )^2+\left ( -a\: \sin(t) \right )^2+\left ( a\: \cos(t) \right )^2}dt \nonumber\nonumber \]
\[d(s)=a. \nonumber\nonumber \]
Then we substitute our parametric equations into \(f(x,y,z)\) to get the function into terms of \(t\)
\[f(x,y,z)=-\sqrt{x^2+y^2}\: \rightarrow\: -\sqrt{(0)^2+(a\: \sin (t))^2}\: \rightarrow \: \: -(\pm a\: \sin(t)) \nonumber \nonumber \]
note that from \( 0 \rightarrow \pi \;\) only \(\; -(a\: \sin(t)) \;\) exists. Likewise from \( \pi \rightarrow 2\pi \;\) only \( -(-a\: \sin(t)) \) exists.
Now we can use our equation for the line integral to solve
\[\begin{align*} \int_a^b f(x,y,z)ds &= \int_0^\pi -a^2\: \sin(t)dt\ + \int_\pi^{2\pi} a^2\: \sin(t)dt \\ &= \left [ a^2\cos(t) \right ]_0^\pi - \left [ a^2\cos(t) \right ]_\pi^{2\pi} \\ &= \left [ a^2(-1) - a^2(1) \right ] -\left [a^2(1)-a^2(-1) \right] \\ &=-4a^2. \end{align*}\nonumber \]
Example \(\PageIndex{5}\)
Integrate over the curve
\[f(x,y)=\dfrac{x^3}{y},\;\;\; \text{line:} \; y=\dfrac{x^2}{2}, \;\;\;0\leq x\leq 2. \nonumber\nonumber \]
Solution
Since all of the equations contain \(x\), there is no need to convert to parametric and solve for \(t\), rather we can just solve for \(x\).
both \(x\) and \(y\) is given so there is no need to convert. The next step would be to find \(d(s)\) in terms of \(x\).
\[x=x, \; y=\dfrac{x^2}{2} \nonumber\nonumber \]
\[d(x)=1 \; \; \; d(y)=x \nonumber\nonumber \]
\[d(s)=\sqrt {\left ( \dfrac{dx}{dx} \right )^2+\left ( \dfrac{dy}{dx} \right )^2}dx \nonumber\nonumber \]
\[d(s)=\sqrt{1^2+x^2}dx \nonumber\nonumber \]
Next we convert the function into a function of \(x\) by substituting in \(y\)
\[ f(x,y)=\dfrac{x^3}{y} \; \rightarrow \; f(x)=\dfrac{x^3}{\dfrac{x^2}{2}} \; \rightarrow \; f(x)= 2x. \nonumber\nonumber \]
Now that we have all the individual parts, the next step is to put it into the equation
\[\int_0^2 2x(\sqrt{1+x^2})dx \nonumber\nonumber \]
we can solve using u substitution
\[u=x^2+1 \: \: \: du=2x\;dx \nonumber\nonumber \]
\[\begin{align*} \int_{0^2+1}^{2^2+1} \sqrt{u} &= \left [\dfrac{2}{3} u^\dfrac {3}{2} \right ]_1^5 \\ &=\dfrac{2}{3} (5\sqrt{5} - 1). \end{align*}\nonumber \]
Example \(\PageIndex{6}\)
Find the area of one side of the "wall" standing orthogonally on the curve \(2x+3y =6\;,0\leq\;x\;\leq 6 \) and beneath the curve on the surface \(f(x,y) = 4+3x+2y.\)
Solution
First, convert \(2x+3y=6\) into parametric form:
\[\text{let}\; x=t \;\;\text{and}\;\; y=\dfrac{6-2x}{3} \:= 2-\dfrac{2t}{3}. \nonumber\nonumber \]
Next, take the rate of change of the arc length (\(ds\)):
\[\dfrac{dx}{dt}=1 \;\;\;\dfrac{dy}{dt}=\dfrac{2}{3} \nonumber\nonumber \]
\[ ds=\sqrt{\left (\dfrac{dx}{dt} \right )^2+\left (\dfrac{dy}{dt} \right )^2}dt=\sqrt{1^2+\left (\dfrac{2}{3} \right )^2}dt=\sqrt{13/9} \; dt=\dfrac{\sqrt{13}}{3}dt. \nonumber\nonumber \]
Solve \(f(x,y)\) in terms of \(t\):
\[f(x,y)=4+3x+2y\;\;\; f(x(t),y(t))=4+3t+2(\dfrac{6-2x}{3}).\nonumber\nonumber \]
Then plug all this information into the equation
\[\begin{align*} \int_a^b f(x(t),y(t))\sqrt {\left ( \dfrac{dx}{dt} \right )^2+ \left ( \dfrac{dy}{dt} \right )^2}dt &= \int_0^6 4+3t+2\left (\dfrac{6-2t}{3}\right )*\left ( \dfrac{\sqrt{13}}{3}\right) \\ &= \left ( \dfrac{\sqrt{13}}{3}\right)\int_0^6 4+3t+4-\dfrac{4}{3}t \; dt \\ &= \dfrac{\sqrt{13}}{3}\int_0^6 8+\dfrac{5}{3} dt \\ &= \dfrac{\sqrt{13}}{3}\left [8t+\dfrac{5}{6}t^2\right]_0^6 \\ & =\dfrac{78\sqrt{13}}{3} \\ \text {Area}&=26\sqrt{13} . \end{align*} \nonumber \]
Contributors
- Danny Nguyen (UCD), Michael Rea (UCD)
- Larry Green (Lake Tahoe Community College)
Integrated by Justin Marshall.

