6.6: Hyperbolic Functions
- Page ID
- 4190
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The hyperbolic functions are a set of functions that have many applications to mathematics, physics, and engineering. Among many other applications, they are used to describe the formation of satellite rings around planets, to describe the shape of a rope hanging from two points, and have application to the theory of special relativity. This section defines the hyperbolic functions and describes many of their properties, especially their usefulness to calculus.
These functions are sometimes referred to as the "hyperbolic trigonometric functions" as there are many, many connections between them and the standard trigonometric functions. Figure \(\PageIndex{1}\) demonstrates one such connection. Just as cosine and sine are used to define points on the circle defined by \(x^2+y^2=1\), the functions hyperbolic cosine and hyperbolic sine are used to define points on the hyperbola \(x^2-y^2=1\).
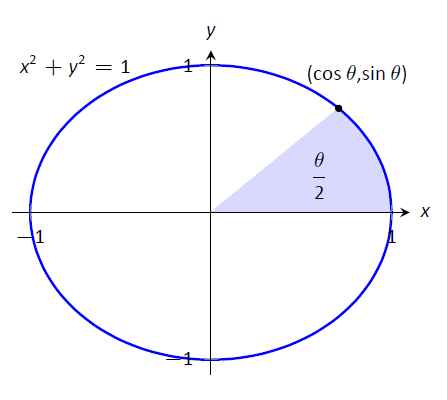
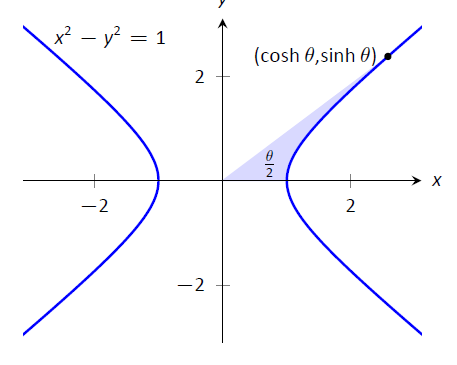
Figure \(\PageIndex{1}\): Using trigonometric functions to define points on a circle and hyperbolic functions to define points on a hyperbola. The area of the shaded regions are included in them.
We begin with their definition.
Definition \(\PageIndex{1}\): Hyperbolic Functions
- \( \cosh x = \frac{e^x+e^{-x}}2\)
- \( \sinh x = \frac{e^x-e^{-x}}2\)
- \(\tanh x = \frac{\sinh x}{\cosh x}\)
- \( \text{sech} x = \frac{1}{\cosh x}\)
- \( \text{csch} x = \frac{1}{\sinh x}\)
- \( \coth x = \frac{\cosh x}{\sinh x}\)
These hyperbolic functions are graphed in Figure \(\PageIndex{2}\). In the graphs of \(\cosh x\) and \(\sinh x\), graphs of \(e^x/2\) and \(e^{-x}/2\) are included with dashed lines. As \(x\) gets "large," \(\cosh x\) and \(\sinh x\) each act like \(e^x/2\); when \(x\) is a large negative number, \(\cosh x\) acts like \(e^{-x}/2\) whereas $\sinh x$ acts like \(-e^{-x}/2\).
Notice the domains of \(\tanh x\) and \(\text{sech} x\) are \((-\infty,\infty)\), whereas both \(\coth x\) and \(\text{csch} x\) have vertical asymptotes at \(x=0\). Also note the ranges of these functions, especially \(\tanh x\): as \(x\to\infty\), both \(\sinh x\) and \(\cosh x\) approach \(e^{-x}/2\), hence \(\tanh x\) approaches \(1\).
The following example explores some of the properties of these functions that bear remarkable resemblance to the properties of their trigonometric counterparts.
Pronunciation Note: "cosh" rhymes with "gosh," "sinh" rhymes with "pinch," and "tanh" rhymes with "ranch."
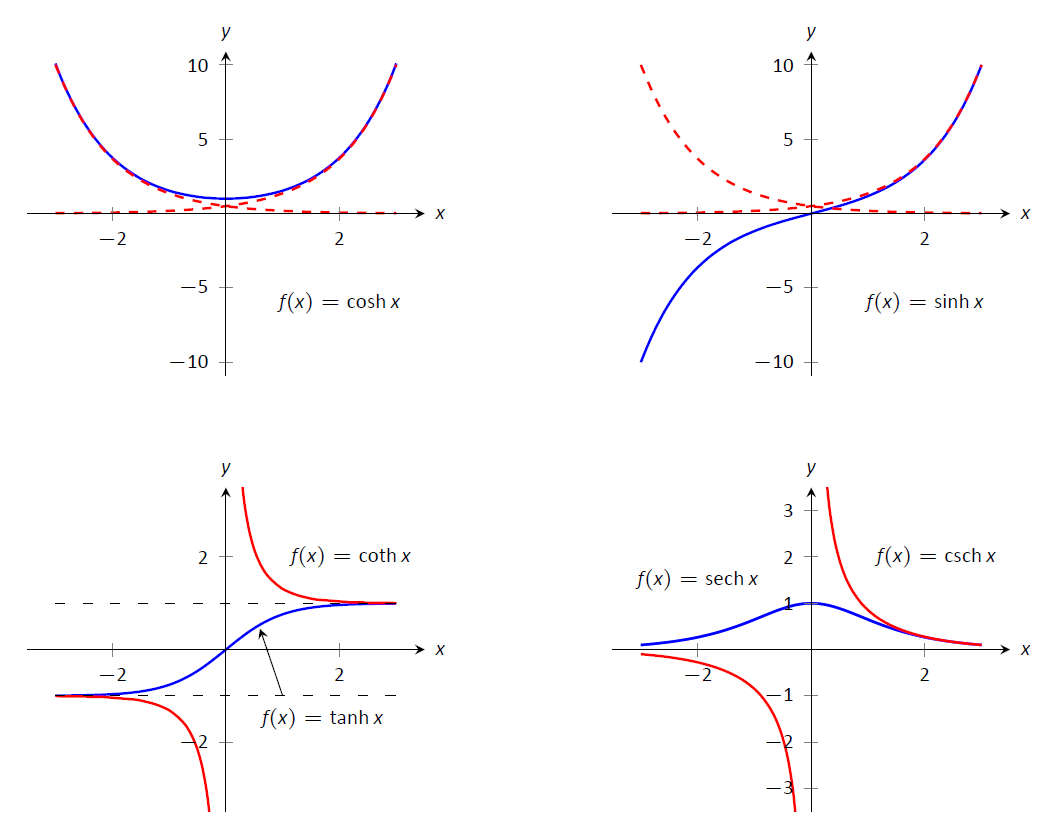
Figure \(\PageIndex{2}\): Graphs of the hyperbolic functions.
Example \(\PageIndex{1}\): Exploring properties of hyperbolic functions
Use Definition \(\PageIndex{1}\) to rewrite the following expressions.
- \(\cosh^2 x-\sinh^2x\)
- \(\tanh^2 x+\text{sech}^2 x\)
- \(2\cosh x\sinh x\)
- \(\frac{d}{dx}\big(\cosh x\big)\)
- \(\frac{d}{dx}\big(\sinh x\big)\)
- \(\frac{d}{dx}\big(\tanh x\big)\)
Solution
- \[\begin{align} \cosh^2x-\sinh^2x &= \left(\frac{e^x+e^{-x}}2\right)^2 -\left(\frac{e^x-e^{-x}}2\right)^2\\ &= \frac{e^{2x}+2e^xe^{-x} + e^{-2x}}4 - \frac{e^{2x}-2e^xe^{-x} + e^{-2x}}4\\ &= \frac44=1.\end{align}\]So \(\cosh^2 x-\sinh^2x=1\).
- \[\begin{align} \tanh^2 x+\text{sech}^2 x &=\frac{\sinh^2x}{\cosh^2 x} + \frac{1}{\cosh^2 x} \\ &= \frac{\sinh^2x+1}{\cosh^2 x}\qquad \text{Now use identity from #1.}\\ &= \frac{\cosh^2 x}{\cosh^2 x} = 1. \end{align}\]So \(\tanh^2 x+\text{sech}^2 x=1\).
- \[\begin{align} 2\cosh x\sinh x &= 2\left(\frac{e^x+e^{-x}}2\right)\left(\frac{e^x-e^{-x}}2\right) \\ &= 2 \cdot\frac{e^{2x} - e^{-2x}}4\\ &= \frac{e^{2x} - e^{-2x}}2 = \sinh (2x).\\ \end{align}\]Thus \(2\cosh x\sinh x = \sinh (2x)\).
- \[\begin{align} \frac{d}{dx}\big(\cosh x\big) &= \frac{d}{dx}\left(\frac{e^x+e^{-x}}2\right) \\ &= \frac{e^x-e^{-x}}2\\ &= \sinh x. \end{align}\]So \(\frac{d}{dx}\big(\cosh x\big) = \sinh x.\)
- \[\begin{align} \frac{d}{dx}\big(\sinh x\big) &= \frac{d}{dx}\left(\frac{e^x-e^{-x}}2\right) \\ &= \frac{e^x+e^{-x}}2\\ &= \cosh x. \end{align}\]So \(\frac{d}{dx}\big(\sinh x\big) = \cosh x.\)
- \[\begin{align} \frac{d}{dx}\big(\tanh x\big) &= \frac{d}{dx}\left(\frac{\sinh x}{\cosh x}\right) \\ &= \frac{\cosh x \cosh x - \sinh x \sinh x}{\cosh^2 x}\\ &= \frac{1}{\cosh^2 x}\\ &=\text{sech}^2 x. \end{align}\]So \(\frac{d}{dx}\big(\tanh x\big) = \text{sech}^2 x.\)
The following Key Idea summarizes many of the important identities relating to hyperbolic functions. Each can be verified by referring back to Definition \(\PageIndex{1}\).
Key Idea 16: Useful Hyperbolic Function Properties
Basic Identities
- \(\cosh^2x-\sinh^2x=1\)
- \(\tanh^2x+\text{sech}^2x=1\)
- \(\coth^2x-\text{csch}^2x = 1\)
- \(\cosh 2x=\cosh^2x+\sinh^2x\)
- \(\sinh 2x = 2\sinh x\cosh x\)
- \(\cosh^2x = \frac{\cosh 2x+1}{2}\)
- \(\sinh^2x=\frac{\cosh 2x-1}{2}\)
Derivatives
- \(\frac{d}{dx}\big(\cosh x\big) = \sinh x\)
- \(\frac{d}{dx}\big(\sinh x\big) = \cosh x\)
- \(\frac{d}{dx}\big(\tanh x\big) = \text{sech}^2 x\)
- \(\frac{d}{dx}\big(\text{sech} x\big) = -\text{sech} x\tanh x\)
- \(\frac{d}{dx}\big(\text{csch} x\big) = -\text{csch} x\coth x\)
- \(\frac{d}{dx}\big(\coth x\big) = -\text{csch}^2x\)
Integrals
- \(\int \cosh x\ dx = \sinh x+C\)
- \(\int \sinh x\ dx = \cosh x+C\)
- \(\int \tanh x\ dx = \ln(\cosh x) +C\)
- \(\int \coth x\ dx = \ln|\sinh x\,|+C\)
We practice using Key Idea 16
Example \(\PageIndex{2}\): Derivatives and integrals of hyperbolic functions
Evaluate the following derivatives and integrals.
- \(\frac{d}{dx}\big(\cosh 2x\big)\)
- \(\int \text{sech}^2(7t-3)\ dt\)
- \( \int_0^{\ln 2} \cosh x\ dx\)
Solution
- Using the Chain Rule directly, we have \(\frac{d}{dx} \big(\cosh 2x\big) = 2\sinh 2x\).
Just to demonstrate that it works, let's also use the Basic Identity found in Key Idea 16: \(\cosh 2x = \cosh^2x+\sinh^2x\).
\[\begin{align}\frac{d}{dx}\big(\cosh 2x\big) = \frac{d}{dx}\big(\cosh^2x+\sinh^2x\big) &= 2\cosh x\sinh x+ 2\sinh x\cosh x\\ &= 4\cosh x\sinh x.\end{align}\]Using another Basic Identity, we can see that \(4\cosh x\sinh x = 2\sinh 2x\). We get the same answer either way. - We employ substitution, with \(u = 7t-3\) and \(du = 7dt\). Applying Key Ideas 10 and 16 we have:
$$ \int\text{sech}^2 (7t-3)\ dt = \frac17\tanh (7t-3) + C.$$ - $$\int_0^{\ln 2} \cosh x\ dx = \sinh x\Big|_0^{\ln 2} = \sinh (\ln 2) - \sinh 0 = \sinh(\ln 2).$$
We can simplify this last expression as \(\sinh x\) is based on exponentials:
$$\sinh(\ln 2) = \frac{e^{\ln 2}-e^{-\ln 2}}2 = \frac{2-1/2}{2} = \frac34.$$
Inverse Hyperbolic Functions
Just as the inverse trigonometric functions are useful in certain integrations, the inverse hyperbolic functions are useful with others. Figure 16 shows the restrictions on the domains to make each function one-to-one and the resulting domains and ranges of their inverse functions. Their graphs are shown in Figure \(\PageIndex{3}\)
Because the hyperbolic functions are defined in terms of exponential functions, their inverses can be expressed in terms of logarithms as shown in Key Idea 17. It is often more convenient to refer to \(\sinh^{-1}x\) than to \(\ln\big(x+\sqrt{x^2+1}\big)\), especially when one is working on theory and does not need to compute actual values. On the other hand, when computations are needed, technology is often helpful but many hand-held calculators lack a \textit{convenient} \(\sinh^{-1}x\) button. (Often it can be accessed under a menu system, but not conveniently.) In such a situation, the logarithmic representation is useful. The reader is not encouraged to memorize these, but rather know they exist and know how to use them when needed.

Table \(\PageIndex{1}\): Graphs of \(\cosh x\), \(\sinh x\) and their inverses.
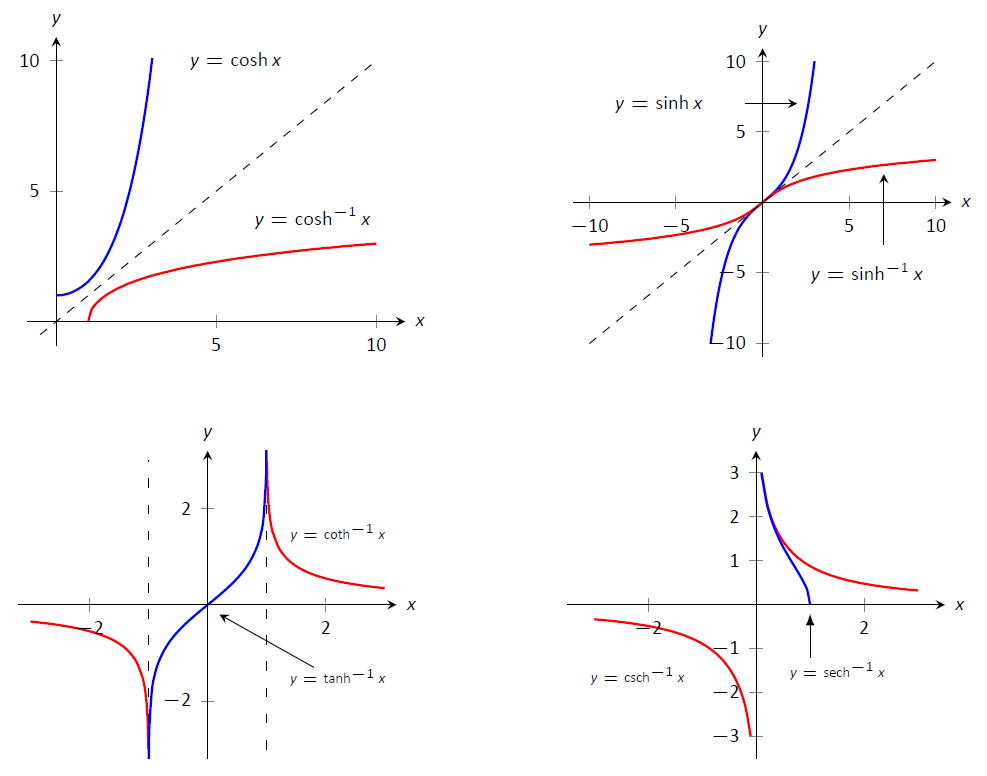
Figure \(\PageIndex{3}\): Graphs of the hyperbolic functions and their inverses.
The following Key Ideas give the derivatives and integrals relating to the inverse hyperbolic functions. In Key Idea 19, both the inverse hyperbolic and logarithmic function representations of the antiderivative are given, based on Key Idea 17. Again, these latter functions are often more useful than the former. Note how inverse hyperbolic functions can be used to solve integrals we used Trigonometric Substitution to solve in Section 6.4.
Key IDea 17: Logarithmic definitions of the inverse hyperbolic functions.
- \(\cosh^{-1}x=\ln\big(x+\sqrt{x^2-1}\big);\ x\geq1\)
- \(\tanh^{-1}x = \frac12\ln\left(\frac{1+x}{1-x}\right);\ |x|<1\)
- \(\text{sech}^{-1}x = \ln\left(\frac{1+\sqrt{1-x^2}}x\right);\ 0<x\leq1\)
- \(\sinh^{-1}x = \ln\big(x+\sqrt{x^2+1}\big)\)
- \(\coth^{-1}x = \frac12\ln\left(\frac{x+1}{x-1}\right);\ |x|>1\)
- \(\text{csch}^{-1}x = \ln\left(\frac1x+\frac{\sqrt{1+x^2}}{|x|}\right);\ x\neq0\)
Key Idea 18: Derivatives Involving Inverse Hyperbolic Functions
- \(\frac{d}{dx}\big(\cosh^{-1} x\big) = \frac{1}{\sqrt{x^2-1}};\ x>1\)
- \(\frac{d}{dx}\big(\sinh^{-1} x\big) = \frac{1}{\sqrt{x^2+1}}\)
- \(\frac{d}{dx}\big(\tanh^{-1} x\big) = \frac{1}{1-x^2};\ |x|<1\)
- \(\frac{d}{dx}\big(\text{sech}^{-1} x\big) = \frac{-1}{x\sqrt{1-x^2}}; 0<x<1\)
- \(\frac{d}{dx}\big(\text{csch}^{-1} x\big) = \frac{-1}{|x|\sqrt{1+x^2}};\ x\neq0\)
- \(\frac{d}{dx}\big(\coth^{-1} x\big) = \frac{1}{1-x^2};\ |x|>1\)
Key Idea 19: Integrals Involving Inverse Hyperbolic Functions
- \(\int \frac{1}{\sqrt{x^2-a^2}}\ dx\) \(=\qquad \cosh^{-1}\left(\frac xa\right)+C;\ 0<a<x\) \(\quad=\ln\Big|x+\sqrt{x^2-a^2}\Big|+C\)
- \(\int \frac{1}{\sqrt{x^2+a^2}}\ dx\) \(=\qquad \sinh^{-1}\left(\frac xa\right)+C;\ a>0\) \(\qquad=\ln\Big|x+\sqrt{x^2+a^2}\Big|+C\)
- \(\int \frac{1}{a^2-x^2}\ dx\) \(=\qquad \left\{\begin{array}{ccc} \frac1a\tanh^{-1}\left(\frac xa\right)+C & & x^2<a^2 \\ \\\frac1a\coth^{-1}\left(\frac xa\right)+C & & a^2<x^2 \end{array}\right.\) \(\quad=\frac1{2a}\ln\left|\frac{a+x}{a-x}\right|+C\)
- \(\int \frac{1}{x\sqrt{a^2-x^2}}\ dx \) \(=\qquad -\frac1a\text{sech}^{-1}\left(\frac xa\right)+C;\ 0<x<a\) \(\quad= \frac1a \ln\left(\frac{x}{a+\sqrt{a^2-x^2}}\right)+C \)
- \(\int \frac{1}{x\sqrt{x^2+a^2}}\ dx\) \(=\qquad -\frac1a\text{csch}^{-1}\left|\frac xa\right| + C;\ x\neq 0,\ a>0\) \(\quad= \frac1a \ln\left|\frac{x}{a+\sqrt{a^2+x^2}}\right|+C\)
We practice using the derivative and integral formulas in the following example.
Example \(\PageIndex{3}\): Derivatives and integrals involving inverse hyperbolic functions
Evaluate the following.
- \( \frac{d}{dx}\left[\cosh^{-1}\left(\frac{3x-2}{5}\right)\right]\)
- \( \int\frac{1}{x^2-1}\ dx\)
- \( \int \frac{1}{\sqrt{9x^2+10}}\ dx\)
Solution
- Applying Key Idea 18 with the Chain Rule gives:
$$\frac{d}{dx}\left[\cosh^{-1}\left(\frac{3x-2}5\right)\right] = \frac{1}{\sqrt{\left(\frac{3x-2}5\right)^2-1}}\cdot\frac35.$$ - Multiplying the numerator and denominator by \((-1)\) gives: \( \int \frac{1}{x^2-1}\ dx = \int \frac{-1}{1-x^2}\ dx\). The second integral can be solved with a direct application of item #3 from Key Idea 19, with \(a=1\). Thus \[ \begin{align} \int \frac{1}{x^2-1}\ dx &= -\int \frac{1}{1-x^2}\ dx \\ &= \left\{\begin{array}{ccc} -\tanh^{-1}\left(x\right)+C & & x^2<1 \\ \\-\coth^{-1}\left(x\right)+C & & 1<x^2 \end{array}\right. \\ &=-\frac12\ln\left|\frac{x+1}{x-1}\right|+C\\ &=\frac12\ln\left|\frac{x-1}{x+1}\right|+C. \end{align}\]
We should note that this exact problem was solved at the beginning of Section 6.5. In that example the answer was given as \(\frac12\ln|x-1|-\frac12\ln|x+1|+C.\) Note that this is equivalent to the answer given in Equation \(\PageIndex{29}\), as \(\ln(a/b) = \ln a - \ln b\).
- This requires a substitution, then item #2 of Key Idea 19 can be applied.
Let \(u = 3x\), hence \(du = 3dx\). We have
\[\int \frac{1}{\sqrt{9x^2+10}}\ dx = \frac13\int\frac{1}{\sqrt{u^2+10}}\ du. \]
Note \(a^2=10\), hence \(a = \sqrt{10}.\) Now apply the integral rule.
\[\begin{align} &= \frac13 \sinh^{-1}\left(\frac{3x}{\sqrt{10}}\right) + C \\&= \frac13 \ln \Big|3x+\sqrt{9x^2+10}\Big|+C. \end{align}\]
This section covers a lot of ground. New functions were introduced, along with some of their fundamental identities, their derivatives and antiderivatives, their inverses, and the derivatives and antiderivatives of these inverses. Four Key Ideas were presented, each including quite a bit of information.
Do not view this section as containing a source of information to be memorized, but rather as a reference for future problem solving. Key Idea 19 contains perhaps the most useful information. Know the integration forms it helps evaluate and understand how to use the inverse hyperbolic answer and the logarithmic answer.
The next section takes a brief break from demonstrating new integration techniques. It instead demonstrates a technique of evaluating limits that return indeterminate forms. This technique will be useful in Section 6.8, where limits will arise in the evaluation of certain definite integrals.
Contributors and Attributions
Gregory Hartman (Virginia Military Institute). Contributions were made by Troy Siemers and Dimplekumar Chalishajar of VMI and Brian Heinold of Mount Saint Mary's University. This content is copyrighted by a Creative Commons Attribution - Noncommercial (BY-NC) License. http://www.apexcalculus.com/
Integrated by Justin Marshall.


