1.7: Curvilinear Coordinates
- Page ID
- 2218
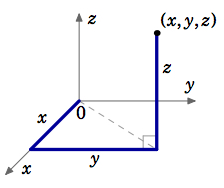
The Cartesian coordinates of a point \((x, y, z)\) are determined by following straight paths starting from the origin: first along the \(x\)-axis, then parallel to the \(y\)-axis, then parallel to the \(z\)-axis, as in Figure 1.7.1. In curvilinear coordinate systems, these paths can be curved. The two types of curvilinear coordinates which we will consider are cylindrical and spherical coordinates. Instead of referencing a point in terms of sides of a rectangular parallelepiped, as with Cartesian coordinates, we will think of the point as lying on a cylinder or sphere. Cylindrical coordinates are often used when there is symmetry around the \(z\)-axis; spherical coordinates are useful when there is symmetry about the origin.
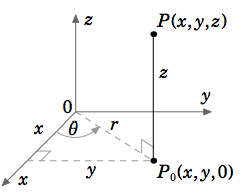
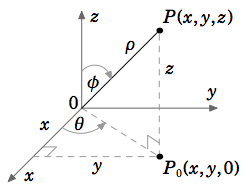
Let \(P = (x, y, z)\) be a point in Cartesian coordinates in \(\mathbb{R}^ 3\), and let \(P_0 = (x, y,0)\) be the projection of \(P\) upon the \(x y\)-plane. Treating \((x, y)\) as a point in \(\mathbb{R}^2\), let \((r,θ)\) be its polar coordinates (see Figure 1.7.2). Let \(ρ\) be the length of the line segment from the origin to \(P\), and let \(φ\) be the angle between that line segment and the positive \(z\)-axis (see Figure 1.7.3). \(φ\) is called the zenith angle. Then the cylindrical coordinates \((r,θ, z)\) and the spherical coordinates \((ρ,θ,φ)\) of \(P(x, y, z)\) are defined as follows:
Cylindrical Coordinates (r,θ, z)
\[\nonumber \begin{split} x &= r \cos θ \qquad r &= \sqrt{ x^ 2 + y^ 2} \\[4pt] \nonumber y &= r \sin θ \qquad θ &= \tan^{−1} \left ( \dfrac{ y}{ x}\right ) \\[4pt] \nonumber z &= z \qquad \qquad z &= z \\[4pt] \end{split}\]
where \(0 ≤ θ ≤ π \text{ if }y ≥ 0 \text{ and }π < θ < 2π \text{ if }y < 0\)
Spherical Coordinates (ρ,θ,φ)
\[\nonumber \begin{split} x &= ρ \sin φ \cos θ \qquad &ρ = \sqrt{ x^ 2 + y^ 2 + z^ 2} \\[4pt] \nonumber y &= ρ \sin φ \sin θ \qquad \qquad &θ = \tan^{−1}\left ( \dfrac{ y}{ x} \right ) \\[4pt] \nonumber z &= ρ \cos φ \qquad \qquad &φ = \cos^{−1} \left ( \dfrac{ z}{ x^ 2+y^ 2+z^ 2} \right ) \\[4pt] \end{split}\]
where \(0 ≤ θ ≤ π \text{ if }y ≥ 0 \text{ and }π < θ < 2π \text{ if }y < 0\)
Both \(θ\) and \(φ\) are measured in radians. Note that \(r ≥ 0, \, 0 ≤ θ < 2π,\, ρ ≥ 0 \text{ and }0 ≤ φ ≤ π\). Also, \(θ\) is undefined when \((x, y) = (0,0)\), and \(φ\) is undefined when \((x, y, z) = (0,0,0)\).
Example 1.31
Convert the point \((−2,−2,1)\) from Cartesian coordinates to (a) cylindrical and (b) spherical coordinates.
Solution
(a) \(r = \sqrt{ (−2)^2 +(−2)^2} = 2\sqrt{ 2},\, θ = \tan^{−1} \left ( \dfrac{−2}{ −2} \right ) = \tan^{−1} (1) = \dfrac{5π}{ 4} ,\text{ since }y = −2 < 0\)
\(∴ (r,θ, z) =\left ( 2 \sqrt{ 2}, \dfrac{5π}{ 4} ,1 \right ) \)
(b) \(ρ = \sqrt{ (−2)^2 +(−2)^2 +1^ 2} = \sqrt{ 9} = 3,\, φ = \cos^{−1} \left ( \dfrac{1}{ 3} \right ) ≈ 1.23 \text{ radians}\).
\(∴ (ρ,θ,φ) = \left ( 3, \dfrac{5π}{ 4} ,1.23 \right ) \)
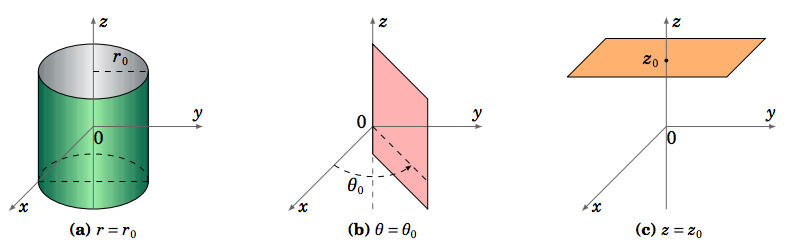
For cylindrical coordinates \((r,θ, z)\), and constants \(r_0 , θ_0 \text{ and }z_0\), we see from Figure 1.7.4 that the surface \(r = r_0\) is a cylinder of radius \(r_0\) centered along the \(z\)-axis, the surface \(θ = θ_0\) is a half-plane emanating from the \(z\)-axis, and the surface \(z = z_0\) is a plane parallel to the \(x y\)-plane.
For spherical coordinates \((ρ,θ,φ)\), and constants \(ρ_0 , θ_0 \text{ and }φ_0\), we see from Figure 1.7.5 that the surface \(ρ = ρ_0\) is a sphere of radius \(ρ_0\) centered at the origin, the surface \(θ = θ_0\) is a half-plane emanating from the \(z\)-axis, and the surface \(φ = φ_0\) is a circular cone whose vertex is at the origin.
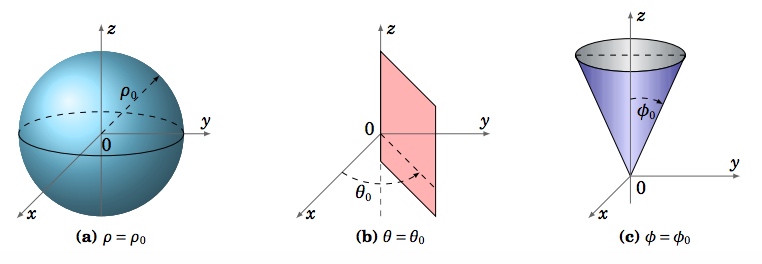
Figures 1.7.4(a) and 1.7.5(a) show how these coordinate systems got their names.
Sometimes the equation of a surface in Cartesian coordinates can be transformed into a simpler equation in some other coordinate system, as in the following example.
Example 1.32
Write the equation of the cylinder \(x^ 2 + y^ 2 = 4\) in cylindrical coordinates.
Since \(r = \sqrt{ x^ 2 + y^ 2}\), then the equation in cylindrical coordinates is \(r = 2\).
Using spherical coordinates to write the equation of a sphere does not necessarily make the equation simpler, if the sphere is not centered at the origin.
Example 1.33
Write the equation \((x−2)^2 +(y−1)^2 + z^ 2 = 9\) in spherical coordinates.
Solution
Multiplying the equation out gives
\[\begin{align}\nonumber x^ 2 + y^ 2 + z^ 2 −4x−2y+5 &= 9 , \text{ so we get} \\[4pt] \nonumber ρ^ 2 −4ρ \sin φ \cos θ −2ρ \sin φ \sin θ −4 &= 0 , \text{ or} \\[4pt] \nonumber ρ^ 2 −2\sin φ(2\cos θ −\sin θ )ρ −4 &= 0 \\[4pt] \end{align}\]
after combining terms. Note that this actually makes it more difficult to figure out what the surface is, as opposed to the Cartesian equation where you could immediately identify the surface as a sphere of radius 3 centered at \((2,1,0)\).
Example 1.34
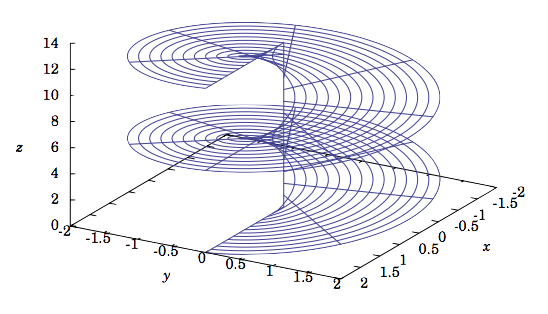
Describe the surface given by \(θ = z\) in cylindrical coordinates.
Solution
This surface is called a helicoid. As the (vertical) \(z\) coordinate increases, so does the angle \(θ\), while the radius \(r\) is unrestricted. So this sweeps out a (ruled!) surface shaped like a spiral staircase, where the spiral has an infinite radius. Figure 1.7.6 shows a section of this surface restricted to \(0 ≤ z ≤ 4π \text{ and }0 ≤ r ≤ 2\).