6.2: Groups of Symmetries
- Page ID
- 7174
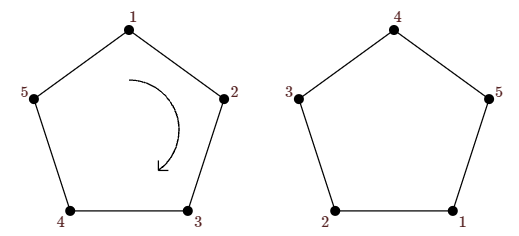
The motions we want to consider can be thought of as permutations, that is, as bijections. For example, the rotation in Figure \(\PageIndex{1}\) can be thought of as the function \(\phi\) given by
\[\eqalign{ \phi(1)&=3\cr \phi(2)&=4\cr \phi(3)&=5\cr \phi(4)&=1\cr \phi(5)&=2,\cr }\nonumber \]
or more compactly we can write this function as \(\pmatrix{ 1&2&3&4&5\cr 3&4&5&1&2\cr }\).
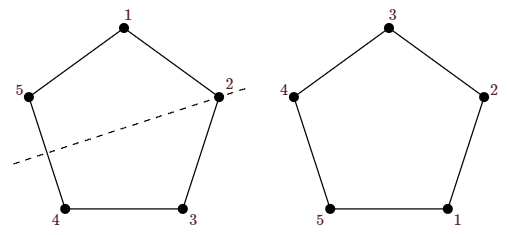
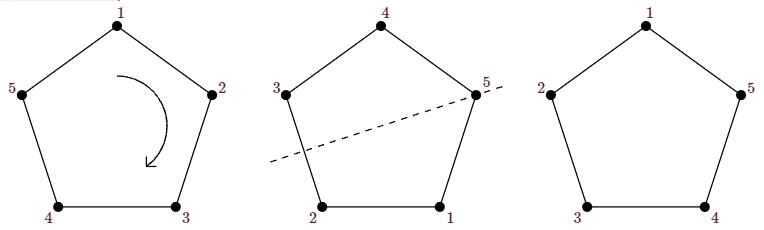
As we would hope, doing two motions in a row corresponds to the compostion of the associated functions. For example, the reflection \(\pmatrix{1&2&3&4&5\cr3&2&1&5&4\cr}\) is shown in Figure \(\PageIndex{2}\). Doing first the rotation of Figure \(\PageIndex{1}\) and then this reflection is shown in Figure \(\PageIndex{3}\), and this does indeed correspond to
\[\pmatrix{1&2&3&4&5\cr 3&2&1&5&4\cr}\circ\pmatrix{1&2&3&4&5\cr 3&4&5&1&2\cr}= \pmatrix{1&2&3&4&5\cr 1&5&4&3&2\cr}.\nonumber\]
With some restrictions, we may choose any permutations of the vertices as the allowable rearrangements giving colorings that are the same. We have discussed the restrictions in general terms; in terms of permuations we require the following: Suppose that \(G\) is a set of permutations that we wish to use to define the "same coloring'' relation. Then the following must be true:
- If \(\phi\) and \(\sigma\) are in \(G\), so is \(\phi\circ\sigma\).
- The identity permutation, \(\id\), is in \(G\).
- If \(\phi\in G\), \(\phi^{-1}\in G\).
If \(G\) has the three properties above it is called a group of permutations.
The group of all permutations of \(\{1,2,\ldots,n\}\) is denoted \(S_n\), the symmetric group on \(n\) items. It satisfies the three required conditions by simple properties of bijections.
In the case of the regular pentagon, there are a number of groups of permutations, but two are of primary interest. The five possible rotations (including the trivial rotation) form a group, the cyclic group of size 5. The total number of "rigid motions'', that is, any combination of rotations and reflections that leave the pentagon superimposed on itself, is 10: Once the position of vertex 1 is established, the other vertices can increase from 1 either clockwise or counterclockwise. The rotations provide all of the former, and it is easy to check that the five reflections provide the counterclockwise positions. This is called a dihedral group and denoted \(D_5\).
Suppose that \(G\) is some group of permutations of an object. If \(\phi\in G\), then \(\phi\) induces a function on the colorings of the object in a natural way, and we can use the same symbol \(\phi\) to represent this function without confusion. If \(c\) is a coloring of the object, then \(\phi(c)\) is the coloring that results by applying \(\phi\) to the colored object, moving the colors with the object. See Figure \(\PageIndex{4}\) for examples. We say that \(G\) acts on the set of colorings \(C\).
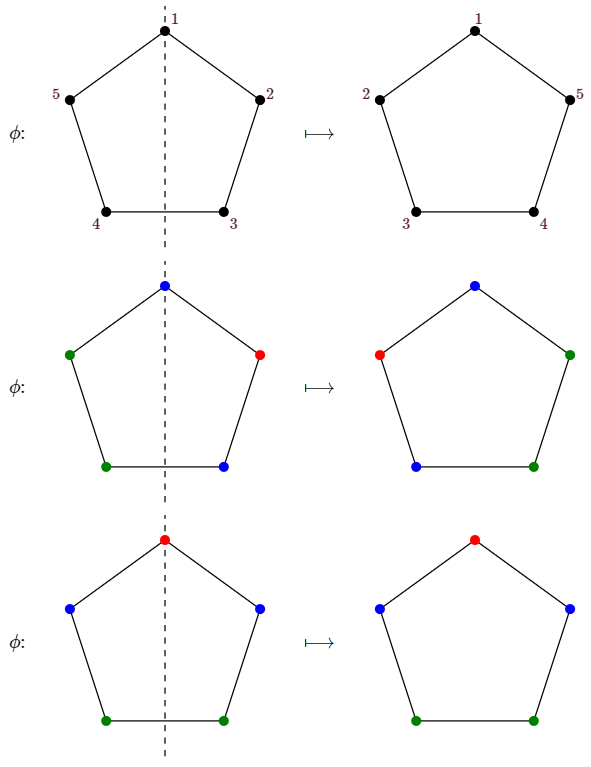
If we apply all permutations in \(G\) to a coloring \(c\), we get all the colorings that we consider to be the same as \(c\) modulo \(G\). More formally, define \(c_1\sim c_2\) if there is a \(\phi\in G\) such that \(\phi(c_1)=c_2\); \(\sim\) is an equivalence relation on the colorings. The equivalence classes, called orbits in this context, group colorings that are the same together. The number of truly different colorings that we want to count is then the number of orbits.
The total number of colorings of the pentagon with \(k\) colors is \(k^5\). If all orbits were the same size, say \(s\), then the number of orbits would be \(k^5/s\). Unfortunately, this is not true. In Figure \(\PageIndex{4}\) we see a coloring whose orbit has size at least 3, but the pentagon with all vertices colored red has orbit size 1.


