6.E: Pólya–Redfield Counting (Exercises)
- Page ID
- 7235
6.2: Groups of Symmetries
Find the 12 permutations of the vertices of the regular tetrahedron corresponding to the 12 rigid motions of the regular tetrahedron. Use the labeling below.
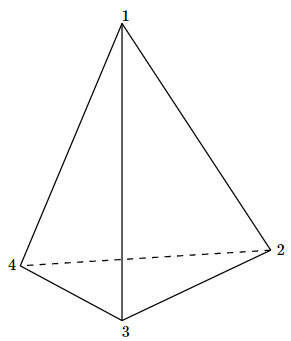
Find the 12 permutations of the edges of the regular tetrahedron corresponding to the 12 rigid motions of the regular tetrahedron. Use the labeling below.
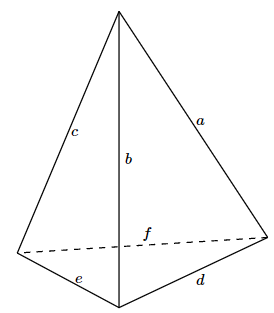
6.3: Burnside's Theorem
Write the 12 permutations of the vertices of the regular tetrahedron corresponding to the 12 rigid motions of the regular tetrahedron in cycle form. Use the labeling below.
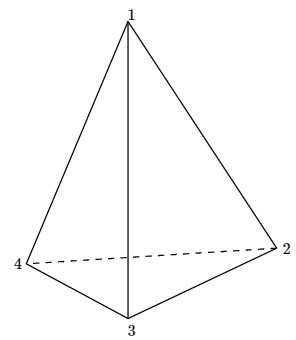
Find the number of different colorings of the vertices of a regular tetrahedron with \(k\) colors, modulo the rigid motions.
Write the 12 permutations of the edges of the regular tetrahedron corresponding to the 12 rigid motions of the regular tetrahedron in cycle form. Use the labeling below.
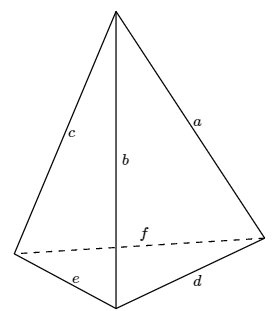
Find the number of different colorings of the edges of a regular tetrahedron with \(k\) colors, modulo the rigid motions.
Find the number of non-isomorphic graphs on 5 vertices "by hand'', that is, using the method of Example 6.3.2.
6.4: Pólya-Redfield Counting
Find the cycle index \(P_G\) for the group of permutations of the vertices of a regular tetrahedron induced by the rigid motions. (See Exercise 6.E.3.1 in Section 6.E.)
Using the previous exercise, write out a full inventory of colorings of the vertices of a regular tetrahedron induced by the rigid motions, with three colors, as in Example 6.4.3. You may use Sage or some other computer algebra system.
Find the cycle index \(P_G\) for the group of permutations of the edges of \(K_5\). (See Exercise 6.E.3.5 in Section 6.E. Don't use the general formula above.)
Using the previous exercise, write out a full inventory of the graphs on five vertices, as in Example 6.4.4. You may use Sage or some other computer algebra system.


