2.4: The Area of a Triangle
- Page ID
- 3257
In elementary geometry you learned that the area of a triangle is one-half the base times the height. We will now use that, combined with some trigonometry, to derive more formulas for the area when given various parts of the triangle.
Case 1: Two sides and the included angle.
Suppose that we have a triangle \(\triangle\,ABC \), in which \(A \) can be either acute, a right angle, or obtuse, as in Figure 2.4.1. Assume that \(A \), \(b \), and \(c \) are known.
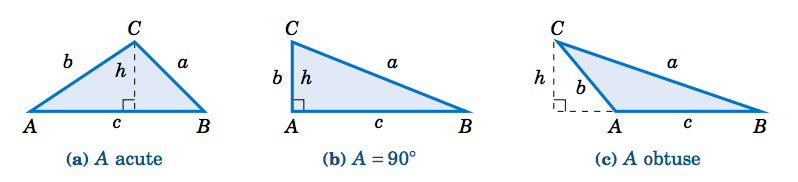
In each case we draw an altitude of height \(h \) from the vertex at \(C \) to \(\overline{AB} \), so that the area (which we will denote by the letter \(K\)) is given by \(K = \frac{1}{2}hc \). But we see that \(h = b\;\sin\;A \) in each of the triangles (since \(\;h=b \) and \(\sin\;A = \sin\;90^\circ = 1 \) in Figure 2.4.1(b), and \(\;h = b\;\sin\;(180^\circ - A) =b\;\sin\;A \) in Figure 2.4.1(c)). We thus get the following formula:
\[\fbox{\(\text{Area} ~=~ K ~=~ \tfrac{1}{2}\,bc\;\sin\;A\)}\label{2.23} \]
The above formula for the area of \(\triangle\,ABC \) is in terms of the known parts \(A \), \(b \), and \(c \). Similar arguments for the angles \(B \) and \(C \) give us:
\[ \begin{align}\text{Area} ~&=~ K =~ \tfrac{1}{2}\,ac\;\sin\;B \\
\text{Area} ~&=~ K =~ \tfrac{1}{2}\,ab\;\sin\;C\label{2.25} \end{align} \]
Notice that the height \(h \) does not appear explicitly in these formulas, although it is implicitly there. These formulas have the advantage of being in terms of parts of the triangle, without having to find \(h \) separately.
Find the area of the triangle \(\triangle\,ABC \) given \(A = 33^\circ \), \(b = 5 \), and \(c = 7 \).

Solution
Using Equation \ref{2.23}, the area \(K \) is given by:
\[ \nonumber \begin{align*}
K ~&=~ \tfrac{1}{2}\,bc\;\sin\;A\\ \nonumber
&=~ \tfrac{1}{2}\,(5)(7)\;\sin\;33^\circ\\ \nonumber
K ~&=~ 9.53
\end{align*} \]
Case 2: Three angles and any side.
Suppose that we have a triangle \(\triangle\,ABC \) in which one side, say, \(a \), and all three angles are known. By the Law of Sines we know that
\[\nonumber
c ~=~ \frac{a\;\sin\;C}{\sin\;A} ~,
\label{2.24}\]
so substituting this into Equation \ref{2.24} we get:
\[\fbox{\(\text{Area} ~=~ K ~=~ \frac{a^2 \;\sin\;B \;\sin\;C}{2\;\sin\;A}
\)}\label{2.26} \]
Similar arguments for the sides \(b \) and \(c \) give us:
\[\begin{align}
\text{Area} ~&=~ K =~ \frac{b^2 \;\sin\;A \;\sin\;C}{2\;\sin\;B}\label{2.27}\\
\text{Area} ~&=~ K =~ \frac{c^2 \;\sin\;A \;\sin\;B}{2\;\sin\;C}\label{2.28}
\end{align} \nonumber \]
Find the area of the triangle \(\triangle\,ABC \) given\ \(A = 115^\circ \), \(B=25^\circ \), \(C=40^\circ \), and \(a = 12 \).
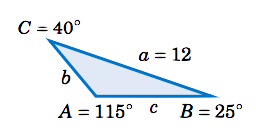
Solution
Using Equation \ref{2.26}, the area \(K \) is given by:
\[\begin{align*}
K ~&=~ \frac{a^2 \;\sin\;B \;\sin\;C}{2\;\sin\;A}\\
&=~ \frac{12^2 \;\sin\;25^\circ \;\sin\;40^\circ}{2\;\sin\;115^\circ}\\
K ~&=~ 21.58
\end{align*} \]
Case 3: Three sides.
Suppose that we have a triangle \(\triangle\,ABC \) in which all three sides are known. Then Heron's formula gives us the area:
For a triangle \(\triangle\,ABC \) with sides \(a \), \(b \), and \(c \), let \(s = \frac{1}{2}\,(a+b+c) \) (i.e. \(2s = a+b+c \) is the perimeter of the triangle). Then the area \(K \) of the triangle is
\[ \text{Area} ~=~ K ~=~ \sqrt{s\,(s-a)\,(s-b)\,(s-c)} ~~.\label{2.29} \]
To prove this, first remember that the area \(K \) is one-half the base times the height. Using \(c \) as the base and the altitude \(h \) as the height, as before in Figure 2.4.1, we have \(K = \frac{1}{2}hc \). Squaring both sides gives us
\[
K^2 = \tfrac{1}{4}\,h^2 c^2 ~.
\label{2.30}\]
In Figure 2.4.2, let \(D \) be the point where the altitude touches \(\overline{AB} \) (or its extension).
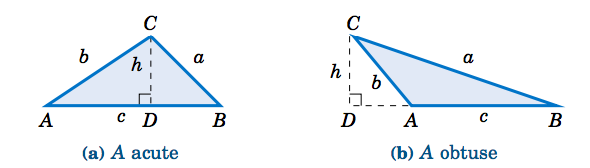
By the Pythagorean Theorem, we see that \(\;h^2 = b^2 - (AD)^2 \). In Figure 2.4.2(a), we see that \(\;AD = b\;\cos\;A \). And in Figure 2.4.2(b) we see that \(\;AD = b\;\cos (180^\circ - A) = -b\cos\;A \). Hence, in either case we have \(\;(AD)^2 = b^2 \;(\cos\;A)^2 \), and so
\[h^2 ~=~ b^2 - b^2 \;(\cos\;A)^2 ~=~ b^2 \,(1 - (\cos\;A)^2 ) ~=~ b^2 \,(1+ \cos\;A)\,(1- \cos\;A)~.\label{2.31} \]
(Note that the above equation also holds when \(A=90^\circ \) since \(\cos\;90^\circ =0 \) and \(h=b\)). Thus, substituting Equation \ref{2.31} into Equation \ref{2.30}, we have
\[
K^2 = \tfrac{1}{4}\,b^2 c^2 \,(1+ \cos\;A)\,(1- \cos\;A) ~.
\label{2.32}\]
By the Law of Cosines we know that
\[\nonumber \begin{align*}
1 + \cos\;A ~&=~ 1 + \frac{b^2 + c^2 - a^2}{2bc} ~=~ \frac{2bc + b^2 + c^2 - a^2}{2bc}
~=~ \frac{(b+c)^2 - a^2}{2bc} ~=~ \frac{((b+c) + a)\,((b+c) - a)}{2bc}\\ \nonumber
&=~ \frac{(a + b + c)\,(b + c - a)}{2bc} ~,
\end{align*} \]
and similarly
\[\nonumber \begin{align*}
1 - \cos\;A ~&=~ 1 - \frac{b^2 + c^2 - a^2}{2bc} ~=~ \frac{2bc - b^2 - c^2 + a^2}{2bc}
~=~ \frac{a^2 - (b-c)^2}{2bc} ~=~ \frac{(a - (b-c))\,(a + (b-c))}{2bc}\\ \nonumber
&=~ \frac{(a - b + c)\,(a + b - c)}{2bc} ~.
\end{align*} \]
Thus, substituting these expressions into Equation \ref{2.32}, we have
\[\nonumber \begin{align}
K^2 ~&=~ \tfrac{1}{4}\,b^2 c^2 \;\frac{(a + b + c)\,(b + c - a)}{2bc} \;\cdot\;
\frac{(a - b + c)\,(a + b - c)}{2bc}\\ \nonumber
&=~ \frac{a + b + c}{2} \;\cdot\; \frac{b + c - a}{2} \;\cdot\; \frac{a - b + c}{2} \;\cdot\;
\frac{a + b - c}{2} ~,\\ \end{align} \nonumber \]
and since we defined \(s = \frac{1}{2}\,(a+b+c) \), we see that
\[\nonumber K^2 ~=~ s\,(s-a)\,(s-b)\,(s-c) ~, \nonumber \]
so upon taking square roots we get
\[\nonumber K ~=~ \sqrt{s\,(s-a)\,(s-b)\,(s-c)} ~~.\quad \textbf{QED} \nonumber \]
Find the area of the triangle \(\triangle\,ABC \) given \(a=5 \), \(b=4 \), and \(c = 7 \).
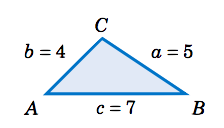
Solution
Using Heron's formula with \(s = \frac{1}{2}\,(a+b+c) = \frac{1}{2}\,(5+4+7) = 8 \), the area \(K \) is given by:
\[ \begin{align*}
K ~&=~ \sqrt{s\,(s-a)\,(s-b)\,(s-c)}\\
&=~ \sqrt{8\,(8-5)\,(8-4)\,(8-7)} ~=~ \sqrt{96} \quad\Rightarrow\quad \boxed{K ~=~ 4\,\sqrt{6}
~\approx~ 9.8} ~.
\end{align*} \]
Heron's formula is useful for theoretical purposes (e.g. in deriving other formulas). However, it is not well-suited for calculator use, exhibiting what is called numerical instability for "extreme'' triangles, as in the following example.
Find the area of the triangle \(\triangle\,ABC \) given \(a=1000000 \), \(b=999999.9999979 \), and \(c = 0.0000029 \).
Solution:
To use Heron's formula, we need to calculate \(s = \frac{1}{2}\,(a+b+c) \). Notice that the actual value of \(a+b+c \) is \(2000000.0000008 \), which has \(14 \) digits. Most calculators can store \(12\)-\(14 \) digits internally (even if they display less), and hence may round off that value of \(a+b+c \) to \(2000000 \). When we then divide that rounded value for \(a+b+c \) by \(2 \) to get \(s \), some calculators (e.g. the TI-83 Plus) will give a rounded down value of \(1000000 \).
This is a problem because \(a=1000000 \), and so we would get \(s-a=0 \), causing Heron's formula to give us an area of \(0 \) for the triangle! And this is indeed the incorrect answer that the TI-83 Plus returns. Other calculators may give some other inaccurate answer, depending on how they store values internally. The actual area - accurate to \(15\) decimal places - is \(K = 0.99999999999895 \), i.e. it is basically \(1 \).
The above example shows how problematic floating-point arithmetic can be. Luckily there is a better formula for the area of a triangle when the three sides are known:
For a triangle \(\triangle\,ABC \) with sides \(a \ge b \ge c \), the area is:
\[ \text{Area} ~=~ K ~=~ \tfrac{1}{4}\,\sqrt{(a + (b+c))\,(c - (a-b))\,(c + (a-b))\,(a + (b-c))}\label{2.33} \]
To use this formula, sort the names of the sides so that \(a \ge b \ge c \). Then perform the operations inside the square root in the exact order in which they appear in the formula, including the use of parentheses. Then take the square root and divide by \(4 \). For the triangle in Example 2.16, the above formula gives an answer of exactly \(K = 1 \) on the same TI-83 Plus calculator that failed with Heron's formula. What is amazing about this formula is that it is just Heron's formula rewritten! The use of parentheses is what forces the correct order of operations for numerical stability.
Another formula for the area of a triangle given its three sides is given below:
For a triangle \(\triangle\,ABC \) with sides \(a \ge b \ge c \), the area is:
\[\label{2.34} \text{Area} ~=~ K ~=~ \tfrac{1}{2}\,\sqrt{a^2 c^2 ~-~ \left( \tfrac{a^2 + c^2 - b^2}{2} \right)^2} \]


