2.5: Circumscribed and Inscribed Circles

Recall from the Law of Sines that any triangle \(\triangle\,ABC\) has a common ratio of sides to sines of opposite angles, namely
\[\nonumber
 \frac{a}{\sin\;A} ~=~ \frac{b}{\sin\;B} ~=~ \frac{c}{\sin\;C} ~.
\]
This common ratio has a geometric meaning: it is the diameter (i.e. twice the radius) of the unique circle in which \(\triangle\,ABC\) can be inscribed, called the circumscribed circle of the triangle. Before proving this, we need to review some elementary geometry.

A central angle of a circle is an angle whose vertex is the center \(O\) of the circle and whose sides (called radii are line segments from \(O\) to two points on the circle. In Figure 2.5.1(a), \(\angle\,O\) is a central angle and we say that it intercepts the arc \(\overparen{BC} \).

Figure 2.5.1 Types of angles in a circle

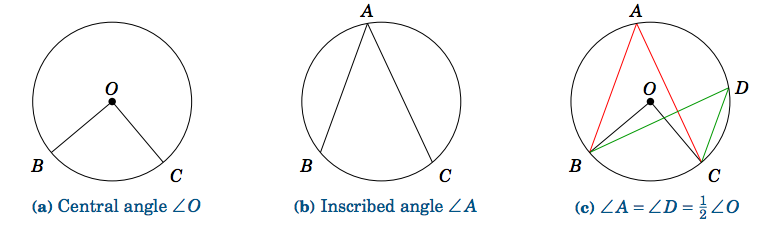
An inscribed angle of a circle is an angle whose vertex is a point \(A\) on the circle and whose sides are line segments (called chords) from \(A\) to two other points on the circle. In Figure 2.5.1(b), \(\angle\,A\) is an inscribed angle that intercepts the arc \(\overparen{BC} \). We state here without proof a useful relation between inscribed and central angles:

Theorem 2.4

If an inscribed angle \(\angle\,A\) and a central angle \(\angle\,O\) intercept the same arc, then \(\angle\,A = \frac{1}{2}\,\angle\,O\, \). Thus, inscribed angles which intercept the same arc are equal.

Figure 2.5.1(c) shows two inscribed angles, \(\angle\,A\) and \(\angle\,D \), which intercept the same arc \(\overparen{BC}\) as the central angle \(\angle\,O \), and hence \(\angle\,A = \angle\,D = \frac{1}{2}\,\angle\,O\) (so \(\;\angle\,O = 2\,\angle\,A = 2\,\angle\,D\,) \).

We will now prove our assertion about the common ratio in the Law of Sines:

Theorem 2.5

For any triangle \(\triangle\,ABC \), the radius \(R\) of its circumscribed circle is given by:

\[2\,R ~=~ \frac{a}{\sin\;A} ~=~ \frac{b}{\sin\;B} ~=~ \frac{c}{\sin\;C}\label{2.35}\]

 

Note: For a circle of diameter \(1 \), this means \(a=\sin\;A \), \(b=\sin\;B \), and \(c=\sin\;C \).)

To prove this, let \(O\) be the center of the circumscribed circle for a triangle \(\triangle\,ABC \). Then \(O\) can be either inside, outside, or on the triangle, as in Figure 2.5.2 below. In the first two cases, draw a perpendicular line segment from \(O\) to \(\overline{AB}\) at the point \(D \).

Figure 2.5.2 Circumscribed circle for \(△ ABC\)

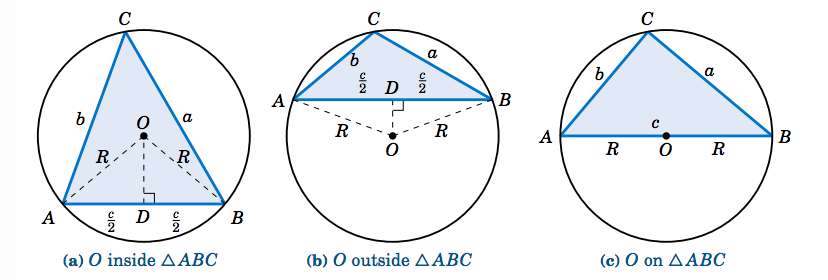
The radii \(\overline{OA}\) and \(\overline{OB}\) have the same length \(R \), so \(\triangle\,AOB\) is an isosceles triangle. Thus, from elementary geometry we know that \(\overline{OD}\) bisects both the angle \(\angle\,AOB\) and the side \(\overline{AB} \). So \(\angle\,AOD = \frac{1}{2}\,\angle\,AOB\) and \(AD = \frac{c}{2} \). But since the inscribed angle \(\angle\,ACB\) and the central angle \(\angle\,AOB\) intercept the same arc \(\overparen{AB} \), we know from Theorem 2.4 that \(\angle\,ACB = \frac{1}{2}\,\angle\,AOB \). Hence, \(\angle\,ACB = \angle\,AOD \). So since \(C =\angle\,ACB \), we have
\[\nonumber
 \sin\;C ~=~ \sin\;\angle\,AOD ~=~ \frac{AD}{OA} ~=~ \frac{\frac{c}{2}}{R} ~=~ \frac{c}{2R}
 \quad\Rightarrow\quad 2\,R ~=~ \frac{c}{\sin\;C} ~,
\]
so by the Law of Sines the result follows if \(O\) is inside or outside \(\triangle\,ABC \).

Now suppose that \(O\) is on \(\triangle\,ABC \), say, on the side \(\overline{AB} \), as in Figure 2.5.2(c). Then \(\overline{AB}\) is a diameter of the circle, so \(C = 90^\circ\) by Thales' Theorem. Hence, \(\sin\;C = 1 \), and so \(2\,R = AB = c = \frac{c}{1} = \frac{c}{\sin\;C}\; \), and the result again follows by the Law of Sines. QED

Example 2.17

Find the radius \(R\) of the circumscribed circle for the triangle \(\triangle\,ABC\) whose sides are \(a=3 \), \(b=4 \), and \(c=5 \).

Figure 2.5.3

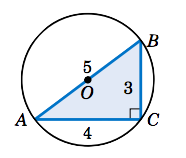
Solution:

We know that \(\triangle\,ABC\) is a right triangle. So as we see from Figure 2.5.3, \(\sin\;A = 3/5 \). Thus,

\[ 2\,R ~=~ \frac{a}{\sin\;A} ~=~ \frac{3}{\frac{3}{5}} ~=~ 5 \quad\Rightarrow\quad
   \boxed{R ~=~ 2.5} ~.\nonumber \]

Note that since \(R =2.5 \), the diameter of the circle is \(5 \), which is the same as \(AB \). Thus, \(\overline{AB}\) must be a diameter of the circle, and so the center \(O\) of the circle is the midpoint of \(\overline{AB} \).

Corollary 2.6

For any right triangle, the hypotenuse is a diameter of the circumscribed circle, i.e. the center of the circle is the midpoint of the hypotenuse.

For the right triangle in the above example, the circumscribed circle is simple to draw; its center can be found by measuring a distance of \(2.5\) units from \(A\) along \(\overline{AB} \).

We need a different procedure for acute and obtuse triangles, since for an acute triangle the center of the circumscribed circle will be inside the triangle, and it will be outside for an obtuse triangle. Notice from the proof of Theorem 2.5 that the center \(O\) was on the perpendicular bisector of one of the sides (\(\overline{AB}\)). Similar arguments for the other sides would show that \(O\) is on the perpendicular bisectors for those sides:

Corollary 2.7

For any triangle, the center of its circumscribed circle is the intersection of the perpendicular bisectors of the sides.

 

Recall from geometry how to create the perpendicular bisector of a line segment: at each endpoint use a compass to draw an arc with the same radius. Pick the radius large enough so that the arcs intersect at two points, as in Figure 2.5.4. The line through those two points is the perpendicular bisector of the line segment. For the circumscribed circle of a triangle, you need the perpendicular bisectors of only two of the sides; their intersection will be the center of the circle.

Figure 2.5.4

Example 2.18

Find the radius \(R\) of the circumscribed circle for the triangle \(\triangle\,ABC\) from Example 2.6 in Section 2.2: \(a = 2 \), \(b = 3 \), and \(c = 4 \). Then draw the triangle and the circle.

Solution:

In Example 2.6 we found \(A=28.9^\circ \), so \(2\,R = \frac{a}{\sin\;A} = \frac{2}{\sin\;28.9^\circ} = 4.14 \), so \(\boxed{R = 2.07}\; \).
In Figure 2.5.5(a) we show how to draw \(\triangle\,ABC\): use a ruler to draw the longest side \(\overline{AB}\) of length \(c=4 \), then use a compass to draw arcs of radius \(3\) and \(2\) centered at \(A\) and \(B \), respectively. The intersection of the arcs is the vertex \(C \).

Figure 2.5.5

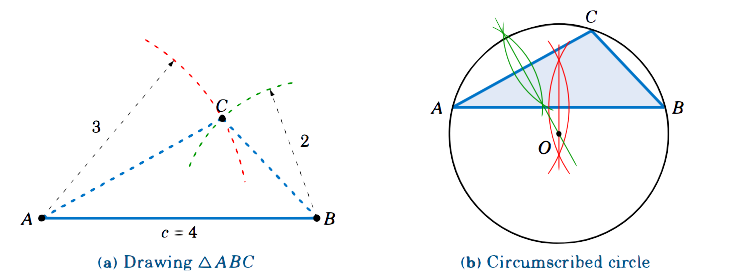
In Figure 2.5.5(b) we show how to draw the circumscribed circle: draw the perpendicular bisectors of \(\overline{AB}\) and \(\overline{AC}\); their intersection is the center \(O\) of the circle. Use a compass to draw the circle centered at \(O\) which passes through \(A \).

Theorem 2.5 can be used to derive another formula for the area of a triangle:

Theorem 2.8

For a triangle \(\triangle\,ABC \), let \(K\) be its area and let \(R\) be the radius of its circumscribed circle. Then

\[K ~=~ \frac{abc}{4\,R} \quad ( \text{and hence }\; R ~=~ \frac{abc}{4\,K} ~) ~. \label{2.36}\]

To prove this, note that by Theorem 2.5 we have
\[\nonumber
 2\,R ~=~ \frac{a}{\sin\;A} ~=~ \frac{b}{\sin\;B} ~=~ \frac{c}{\sin\;C} \quad\Rightarrow\quad
  \sin\;A ~=~ \frac{a}{2\,R} ~,~~ \sin\;B ~=~ \frac{b}{2\,R} ~,~~ \sin\;C ~=~ \frac{c}{2\,R} ~.
\]
Substitute those expressions into Equation 2.26 from Section 2.4 for the area \(K\):
\[\nonumber
 K ~=~ \frac{a^2 \;\sin\;B \;\sin\;C}{2\;\sin\;A} ~=~
  \frac{a^2 \;\cdot\; \frac{b}{2\,R} \;\cdot\; \frac{c}{2\,R}}{2\;\cdot\; \frac{a}{2\,R}}
  ~=~ \frac{abc}{4\,R}  \qquad \textbf{QED}
\]

Combining Theorem 2.8 with Heron's formula for the area of a triangle, we get:

Corollary 2.9

For a triangle \(\triangle\,ABC \), let \(s = \frac{1}{2}(a+b+c) \). Then the radius \(R\) of its circumscribed circle is

\[R ~=~ \frac{abc}{4\,\sqrt{s\,(s-a)\,(s-b)\,(s-c)}} ~~.\label{2.37}\]

In addition to a circumscribed circle, every triangle has an inscribed circle, i.e. a circle to which the sides of the triangle are tangent, as in Figure 2.5.6.

Figure 2.5.6 Inscribed circle for \(△ ABC\)

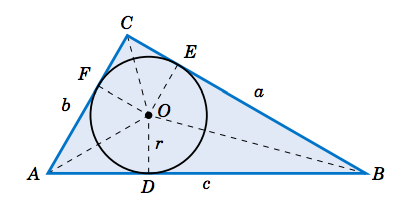
Let \(r\) be the radius of the inscribed circle, and let \(D \), \(E \), and \(F\) be the points on \(\overline{AB} \), \(\overline{BC} \), and \(\overline{AC} \), respectively, at which the circle is tangent. Then \(\overline{OD} \perp \overline{AB} \), \(\overline{OE} \perp \overline{BC} \), and \(\overline{OF} \perp \overline{AC} \). Thus, \(\triangle\,OAD\) and \(\triangle\,OAF\) are equivalent triangles, since they are right triangles with the same hypotenuse \(\overline{OA}\) and with corresponding legs \(\overline{OD}\) and \(\overline{OF}\) of the same length \(r \). Hence, \(\angle\,OAD =\angle\,OAF \), which means that \(\overline{OA}\) bisects the angle \(A \). Similarly, \(\overline{OB}\) bisects \(B\) and \(\overline{OC}\) bisects \(C \). We have thus shown:

For any triangle, the center of its inscribed circle is the intersection of the bisectors of the angles.

We will use Figure 2.5.6 to find the radius \(r\) of the inscribed circle. Since \(\overline{OA}\) bisects \(A \), we see that \(\tan\;\frac{1}{2}A = \frac{r}{AD} \), and so \(r = AD \,\cdot\, \tan\;\frac{1}{2}A \). Now, \(\triangle\,OAD\) and \(\triangle\,OAF\) are equivalent triangles, so \(AD =AF \). Similarly, \(DB = EB\) and \(FC = CE \). Thus, if we let \(s=\frac{1}{2}(a+b+c) \), we see that
\[\nonumber\begin{align*}
 2\,s ~&=~ a ~+~ b ~+~ c ~=~ (AD + DB ) ~+~ (CE + EB) ~+~ (AF + FC)\\ \nonumber
 &=~ AD ~+~ EB ~+~ CE ~+~ EB ~+~ AD ~+~ CE ~=~ 2\,(AD + EB + CE)\\ \nonumber
 s ~&=~ AD ~+~ EB ~+~ CE ~=~ AD ~+~ a\\ \nonumber 
 AD ~&=~ s - a ~.
\end{align*}\]
Hence, \(r = (s-a)\,\tan\;\frac{1}{2}A \). Similar arguments for the angles \(B\) and \(C\) give us:

Theorem 2.10

For any triangle \(\triangle\,ABC \), let \(s = \frac{1}{2}(a+b+c) \). Then the radius \(r\) of its inscribed circle is

\[ r ~=~ (s-a)\,\tan\;\tfrac{1}{2}A ~=~ (s-b)\,\tan\;\tfrac{1}{2}B ~=~
  (s-c)\,\tan\;\tfrac{1}{2}C ~.\label{2.38}\]

We also see from Figure 2.5.6 that the area of the triangle \(\triangle\,AOB\) is
\[\nonumber 
 \text{Area}(\triangle\,AOB) ~=~ \tfrac{1}{2}\,\text{base} \times \text{height} ~=~
  \tfrac{1}{2}\,c\,r ~.
\]
Similarly, \(\text{Area}(\triangle\,BOC) = \frac{1}{2}\,a\,r\) and \(\text{Area}(\triangle\,AOC) = \frac{1}{2}\,b\,r \). Thus, the area \(K\) of \(\triangle\,ABC\) is
\[\nonumber \begin{align*}
 K ~&=~ \text{Area}(\triangle\,AOB) ~+~\text{Area}(\triangle\,BOC) ~+~ \text{Area}(\triangle\,AOC)
  ~=~ \tfrac{1}{2}\,c\,r ~+~ \tfrac{1}{2}\,a\,r ~+~ \tfrac{1}{2}\,b\,r\\ \nonumber
 &=~ \tfrac{1}{2}\,(a+b+c)\,r ~=~ sr ~,~\text{so by Heron's formula we get}\\ \nonumber
 r ~&=~ \frac{K}{s} ~=~ \frac{\sqrt{s\,(s-a)\,(s-b)\,(s-c)}}{s} ~=~
  \sqrt{\frac{s\,(s-a)\,(s-b)\,(s-c)}{s^2}} ~=~ \sqrt{\frac{(s-a)\,(s-b)\,(s-c)}{s}} ~~.
\end{align*}\]
We have thus proved the following theorem:

Theorem 2.11

For any triangle \(\triangle\,ABC \), let \(s = \frac{1}{2}(a+b+c) \). Then the radius \(r\) of its inscribed circle is

\[\label{2.39}r ~=~ \frac{K}{s} ~=~ \sqrt{\frac{(s-a)\,(s-b)\,(s-c)}{s}} ~~.\]

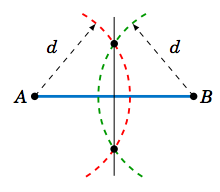
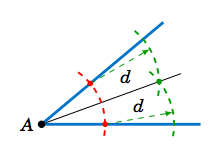
Recall from geometry how to bisect an angle: use a compass centered at the vertex to draw an arc that intersects the sides of the angle at two points. At those two points use a compass to draw an arc with the same radius, large enough so that the two arcs intersect at a point, as in Figure 2.5.7. The line through that point and the vertex is the bisector of the angle. For the inscribed circle of a triangle, you need only two angle bisectors; their intersection will be the center of the circle.

Figure 2.5.7

Example 2.19

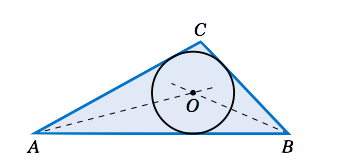
Find the radius \(r\) of the inscribed circle for the triangle \(\triangle\,ABC\) from Example 2.6 in Section 2.2: \(a = 2 \), \(b = 3 \), and \(c = 4 \). Draw the circle.

Figure 2.5.8

Solution:

Using Theorem 2.11 with \(s = \frac{1}{2}(a+b+c) =\frac{1}{2}(2+3+4) = \frac{9}{2} \), we have

\[ r ~=~ \sqrt{\frac{(s-a)\,(s-b)\,(s-c)}{s}} ~=~
   \sqrt{\frac{\left(\frac{9}{2}-2\right)\,\left(\frac{9}{2}-3\right)\,\left(\frac{9}{2}-
   4\right)}{\frac{9}{2}}} ~=~ \sqrt{\frac{5}{12}}~.\nonumber \]

Figure 2.5.8 shows how to draw the inscribed circle: draw the bisectors of \(A\) and \(B \), then at their intersection use a compass to draw a circle of radius \(r = \sqrt{5/12} \approx 0.645 \).

 

Contributors

• Michael Corral (Schoolcraft College). The content of this page is distributed under the terms of the GNU Free Documentation License, Version 1.2.