5.E: Trigonometric Functions (Exercises)
- Page ID
- 5972
5.1: Angles
In this section, we will examine properties of angles.
Verbal
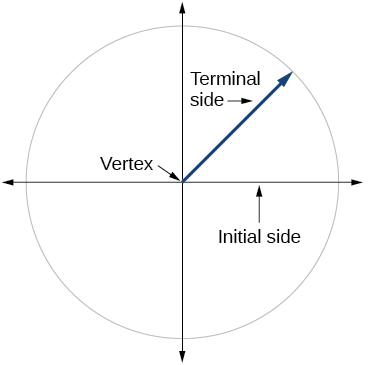
1) Draw an angle in standard position. Label the vertex, initial side, and terminal side.
- Answer
-
2) Explain why there are an infinite number of angles that are coterminal to a certain angle.
3) State what a positive or negative angle signifies, and explain how to draw each.
- Answer
-
Whether the angle is positive or negative determines the direction. A positive angle is drawn in the counterclockwise direction, and a negative angle is drawn in the clockwise direction.
4) How does radian measure of an angle compare to the degree measure? Include an explanation of \(1\) radian in your paragraph.
5) Explain the differences between linear speed and angular speed when describing motion along a circular path.
- Answer
-
Linear speed is a measurement found by calculating distance of an arc compared to time. Angular speed is a measurement found by calculating the angle of an arc compared to time.
Graphical
For the exercises 6-21, draw an angle in standard position with the given measure.
6) \(30^{\circ}\)
7) \(300^{\circ}\)
- Answer
-
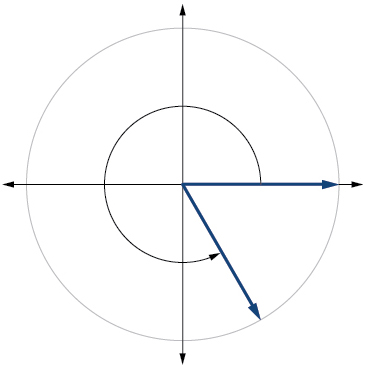
8) \(-80^{\circ}\)
9) \(135^{\circ}\)
- Answer
-
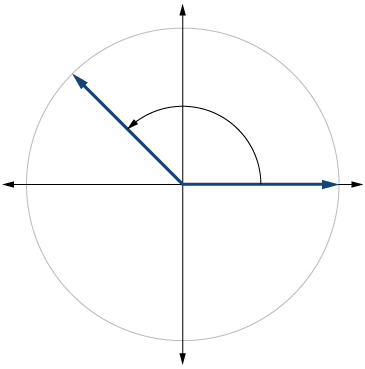
10) \(-150^{\circ}\)
11) \(\dfrac{2π}{3}\)
- Answer
-
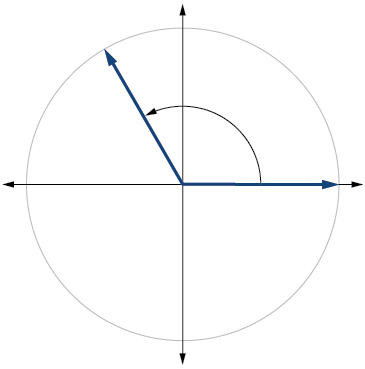
12) \(\dfrac{7π}{4}\)
13) \(\dfrac{5π}{6}\)
- Answer
-
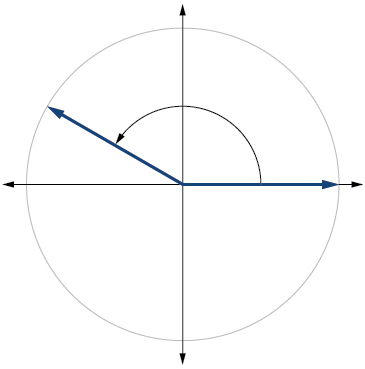
14) \(\dfrac{π}{2}\)
15) \(−\dfrac{π}{10}\)
- Answer
-
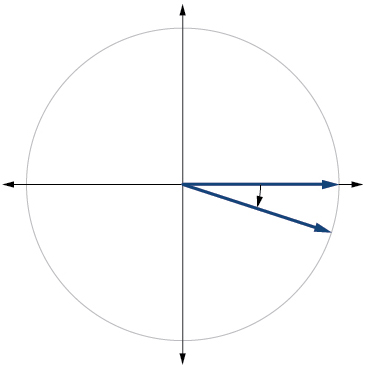
16) \(415^{\circ}\)
17) \(-120^{\circ}\)
- Answer
-
\(240^{\circ}\)
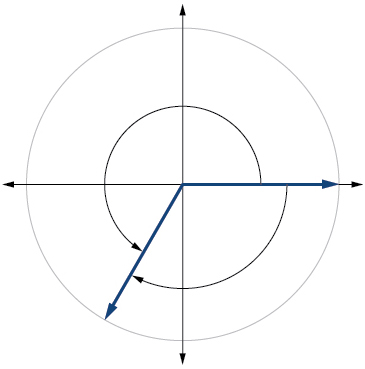
18) \(-315^{\circ}\)
19)\(\dfrac{22π}{3}\)
- Answer
-
\(\dfrac{4π}{3}\)
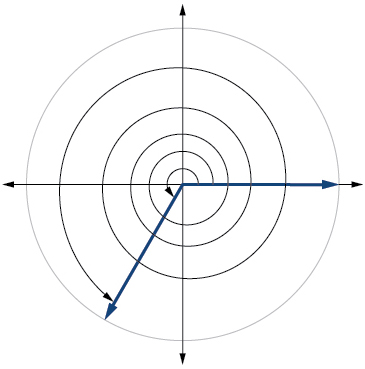
20) \(−\dfrac{π}{6}\)
21) \(−\dfrac{4π}{3}\)
- Answer
-
\(\dfrac{2π}{3}\)
For the exercises 22-23, refer to Figure below. Round to two decimal places.
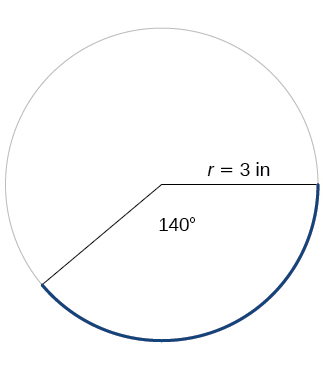
22) Find the arc length.
23) Find the area of the sector.
- Answer
-
\(\dfrac{27π}{2}≈11.00 \text{ in}^2\)
For the exercises 24-25, refer to Figure below. Round to two decimal places.
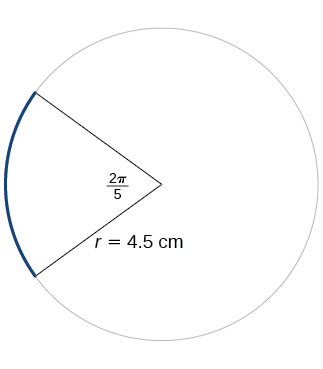
24) Find the arc length.
25) Find the area of the sector.
- Answer
-
\(\dfrac{81π}{20}≈12.72\text{ cm}^2\)
Algebraic
For the exercises 26-32, convert angles in radians to degrees.
26) \(\dfrac{3π}{4}\) radians
27) \(\dfrac{π}{9}\) radians
- Answer
-
\(20^{\circ}\)
28) \(−\dfrac{5π}{4}\) radians
29) \(\dfrac{π}{3}\) radians
- Answer
-
\(60^{\circ}\)
30) \(−\dfrac{7π}{3}\) radians
31) \(−\dfrac{5π}{12}\) radians
- Answer
-
\(-75^{\circ}\)
32) \(\dfrac{11π}{6}\) radians
For the exercises 33-39, convert angles in degrees to radians.
33) \(90^{\circ}\)
- Answer
-
\(\dfrac{π}{2}\) radians
34) \(100^{\circ}\)
35) \(-540^{\circ}\)
- Answer
-
\(−3π\) radians
36) \(-120^{\circ}\)
37) \(180^{\circ}\)
- Answer
-
\(π\) radians
38) \(-315^{\circ}\)
39) \(150^{\circ}\)
- Answer
-
\(\dfrac{5π}{6}\) radians
For the exercises 40-45, use to given information to find the length of a circular arc. Round to two decimal places.
40) Find the length of the arc of a circle of radius \(12\) inches subtended by a central angle of \(\dfrac{π}{4}\) radians.
41) Find the length of the arc of a circle of radius \(5.02\) miles subtended by the central angle of \(\dfrac{π}{3}\).
- Answer
-
\(\dfrac{5.02π}{3}≈5.26\) miles
42) Find the length of the arc of a circle of diameter \(14\) meters subtended by the central angle of \(\dfrac{5\pi }{6}\).
43) Find the length of the arc of a circle of radius \(10\) centimeters subtended by the central angle of \(50^{\circ}\).
- Answer
-
\(\dfrac{25π}{9}≈8.73\) centimeters
44) Find the length of the arc of a circle of radius \(5\) inches subtended by the central angle of \(220^{circ}\).
45) Find the length of the arc of a circle of diameter \(12\) meters subtended by the central angle is \(63^{circ}\).
- Answer
-
\(\dfrac{21π}{10}≈6.60\) meters
For the exercises 46-49, use the given information to find the area of the sector. Round to four decimal places.
46) A sector of a circle has a central angle of \(45^{\circ}\) and a radius \(6\) cm.
47) A sector of a circle has a central angle of \(30^{\circ}\) and a radius of \(20\) cm.
- Answer
-
\(104.7198\; cm^2\)
48) A sector of a circle with diameter \(10\) feet and an angle of \(\dfrac{π}{2}\) radians.
49) A sector of a circle with radius of \(0.7\) inches and an angle of \(π\) radians.
- Answer
-
\(0.7697\; in^2\)
For the exercises 50-53, find the angle between \(0^{\circ}\) and \(360^{\circ}\) that is coterminal to the given angle.
50) \(-40^{\circ}\)
51) \(-110^{\circ}\)
- Answer
-
\(250^{\circ}\)
52) \(700^{\circ}\)
53) \(1400^{\circ}\)
- Answer
-
\(320^{\circ}\)
For the exercises 54-57, find the angle between \(0\) and \(2\pi \) in radians that is coterminal to the given angle.
54) \(−\dfrac{π}{9}\)
55) \(\dfrac{10π}{3}\)
- Answer
-
\(\dfrac{4π}{3}\)
56) \(\dfrac{13π}{6}\)
57) \(\dfrac{44π}{9}\)
- Answer
-
\(\dfrac{8π}{9}\)
Real-World Applications
58) A truck with \(32\)-inch diameter wheels is traveling at \(60\) mi/h. Find the angular speed of the wheels in rad/min. How many revolutions per minute do the wheels make?
59) A bicycle with \(24\)-inch diameter wheels is traveling at \(15\) mi/h. Find the angular speed of the wheels in rad/min. How many revolutions per minute do the wheels make?
- Answer
-
\(1320\) rad \(210.085\) RPM
60) A wheel of radius \(8\) inches is rotating \(15^{\circ}/s\). What is the linear speed \(v\), the angular speed in RPM, and the angular speed in rad/s?
61) A wheel of radius \(14\) inches is rotating \(0.5 \text{rad/s}\). What is the linear speed \(v\), the angular speed in RPM, and the angular speed in deg/s?
- Answer
-
\(7\) in./s, \(4.77\) RPM, \(28.65\) deg/s
62) A CD has diameter of \(120\) millimeters. When playing audio, the angular speed varies to keep the linear speed constant where the disc is being read. When reading along the outer edge of the disc, the angular speed is about \(200\) RPM (revolutions per minute). Find the linear speed.
63) When being burned in a writable CD-R drive, the angular speed of a CD is often much faster than when playing audio, but the angular speed still varies to keep the linear speed constant where the disc is being written. When writing along the outer edge of the disc, the angular speed of one drive is about \(4800\) RPM (revolutions per minute). Find the linear speed if the CD has diameter of \(120\) millimeters.
- Answer
-
\(1,809,557.37 \text{ mm/min}=30.16 \text{ m/s}\)
64) A person is standing on the equator of Earth (radius \(3960\) miles). What are his linear and angular speeds?
65) Find the distance along an arc on the surface of Earth that subtends a central angle of \(5\) minutes \((1 \text{ minute}=\dfrac{1}{60} \text{ degree})\). The radius of Earth is \(3960\) miles.
- Answer
-
\(5.76\) miles
66) Find the distance along an arc on the surface of Earth that subtends a central angle of \(7\) minutes \((1 \text{ minute}=\dfrac{1}{60} \text{ degree})\). The radius of Earth is \(3960\) miles.
67) Consider a clock with an hour hand and minute hand. What is the measure of the angle the minute hand traces in \(20\) minutes?
- Answer
-
\(120°\)
Extensions
68) Two cities have the same longitude. The latitude of city A is \(9.00\) degrees north and the latitude of city B is \(30.00\) degree north. Assume the radius of the earth is \(3960\) miles. Find the distance between the two cities.
69) A city is located at \(40\) degrees north latitude. Assume the radius of the earth is \(3960\) miles and the earth rotates once every \(24\) hours. Find the linear speed of a person who resides in this city.
- Answer
-
\(794\) miles per hour
70) A city is located at \(75\) degrees north latitude. Assume the radius of the earth is \(3960\) miles and the earth rotates once every \(24\) hours. Find the linear speed of a person who resides in this city.
71) Find the linear speed of the moon if the average distance between the earth and moon is \(239,000\) miles, assuming the orbit of the moon is circular and requires about \(28\) days. Express answer in miles per hour.
- Answer
-
\(2,234\) miles per hour
72) A bicycle has wheels \(28\) inches in diameter. A tachometer determines that the wheels are rotating at \(180\) RPM (revolutions per minute). Find the speed the bicycle is traveling down the road.
73) A car travels \(3\) miles. Its tires make \(2640\) revolutions. What is the radius of a tire in inches?
- Answer
-
\(11.5\) inches
74) A wheel on a tractor has a \(24\)-inch diameter. How many revolutions does the wheel make if the tractor travels \(4\) miles?
5.2: Unit Circle - Sine and Cosine Functions
Verbal
1) Describe the unit circle.
- Answer
-
The unit circle is a circle of radius \(1\) centered at the origin.
2) What do the \(x\)- and \(y\)-coordinates of the points on the unit circle represent?
3) Discuss the difference between a coterminal angle and a reference angle.
- Answer
-
Coterminal angles are angles that share the same terminal side. A reference angle is the size of the smallest acute angle, \(t\), formed by the terminal side of the angle \(t\) and the horizontal axis.
4) Explain how the cosine of an angle in the second quadrant differs from the cosine of its reference angle in the unit circle.
5) Explain how the sine of an angle in the second quadrant differs from the sine of its reference angle in the unit circle.
- Answer
-
The sine values are equal.
Algebraic
For the exercises 6-9, use the given sign of the sine and cosine functions to find the quadrant in which the terminal point determined by \(t\) lies.
6) \( \sin (t)<0\) and \( \cos (t)<0\)
7) \( \sin (t)>0\) and \( \cos (t)>0\)
- Answer
-
\(\textrm{I}\)
8) \( \sin (t)>0 \) and \( \cos (t)<0\)
9) \( \sin (t)<0 \) and \( \cos (t)>0\)
- Answer
-
\(\textrm{IV}\)
For the exercises 10-22, find the exact value of each trigonometric function.
10) \(\sin \dfrac{π}{2}\)
11) \(\sin \dfrac{π}{3}\)
- Answer
-
\(\dfrac{\sqrt{3}}{2}\)
12) \( \cos \dfrac{π}{2}\)
13) \( \cos \dfrac{π}{3}\)
- Answer
-
\(\dfrac{1}{2}\)
14) \( \sin \dfrac{π}{4}\)
15) \( \cos \dfrac{π}{4}\)
- Answer
-
\(\dfrac{\sqrt{2}}{2}\)
16) \( \sin \dfrac{π}{6}\)
17) \( \sin π\)
- Answer
-
\(0\)
18) \( \sin \dfrac{3π}{2}\)
19) \( \cos π\)
- Answer
-
\(−1\)
20) \( \cos 0\)
21) \(cos \dfrac{π}{6}\)
- Answer
-
\(\dfrac{\sqrt{3}}{2}\)
22) \( \sin 0\)
Numeric
For the exercises 23-33, state the reference angle for the given angle.
23) \(240°\)
- Answer
-
\(60°\)
24) \(−170°\)
25) \(100°\)
- Answer
-
\(80°\)
26) \(−315°\)
27) \(135°\)
- Answer
-
\(45°\)
28) \(\dfrac{5π}{4}\)
29) \(\dfrac{2π}{3}\)
- Answer
-
\(\dfrac{π}{3}\)
30) \(\dfrac{5π}{6}\)
31) \(−\dfrac{11π}{3}\)
- Answer
-
\(\dfrac{π}{3}\)
32) \(\dfrac{−7π}{4}\)
33) \(\dfrac{−π}{8}\)
- Answer
-
\(\dfrac{π}{8}\)
For the exercises 34-49, find the reference angle, the quadrant of the terminal side, and the sine and cosine of each angle. If the angle is not one of the angles on the unit circle, use a calculator and round to three decimal places.
34) \(225°\)
35) \(300°\)
- Answer
-
\(60°\), Quadrant IV, \( \sin (300°)=−\dfrac{\sqrt{3}}{2}, \cos (300°)=\dfrac{1}{2}\)
36) \(320°\)
37) \(135°\)
- Answer
-
\(45°\), Quadrant II, \( \sin (135°)=\dfrac{\sqrt{2}}{2}, \cos (135°)=−\dfrac{\sqrt{2}}{2}\)
38) \(210°\)
39) \(120°\)
- Answer
-
\(60°\), Quadrant II, \(\sin (120°)=\dfrac{\sqrt{3}}{2}\), \(\cos (120°)=−\dfrac{1}{2}\)
40) \(250°\)
41) \(150°\)
- Answer
-
\(30°\), Quadrant II, \( \sin (150°)=\frac{1}{2}\), \(\cos(150°)=−\dfrac{\sqrt{3}}{2}\)
42) \(\dfrac{5π}{4}\)
43) \(\dfrac{7π}{6}\)
- Answer
-
\(\dfrac{π}{6}\), Quadrant III, \(\sin \left( \dfrac{7π}{6}\right )=−\dfrac{1}{2}\), \(\cos \left (\dfrac{7π}{6} \right)=−\dfrac{\sqrt{3}}{2}\)
44) \(\dfrac{5π}{3}\)
45) \(\dfrac{3π}{4}\)
- Answer
-
\(\dfrac{π}{4}\), Quadrant II, \(\sin \left(\dfrac{3π}{4}\right)=\dfrac{\sqrt{2}}{2}\), \(\cos\left(\dfrac{4π}{3}\right)=−\dfrac{\sqrt{2}}{2}\)
46) \(\dfrac{4π}{3}\)
47) \(\dfrac{2π}{3}\)
- Answer
-
\(\dfrac{π}{3}\), Quadrant II, \( \sin \left(\dfrac{2π}{3}\right)=\dfrac{\sqrt{3}}{2}\), \( \cos \left(\dfrac{2π}{3}\right)=−\dfrac{1}{2}\)
48) \(\dfrac{5π}{6}\)
49) \(\dfrac{7π}{4}\)
- Answer
-
\(\dfrac{π}{4}\), Quadrant IV, \( \sin \left(\dfrac{7π}{4}\right)=−\dfrac{\sqrt{2}}{2}\), \( \cos \left(\dfrac{7π}{4}\right)=\dfrac{\sqrt{2}}{2}\)
For the exercises 50-59, find the requested value.
50) If \(\cos (t)=\dfrac{1}{7}\) and \(t\) is in the \(4^{th}\) quadrant, find \( \sin (t)\).
51) If \( \cos (t)=\dfrac{2}{9}\) and \(t\) is in the \(1^{st}\) quadrant, find \(\sin (t)\).
- Answer
-
\(\dfrac{\sqrt{77}}{9}\)
52) If \(\sin (t)=\dfrac{3}{8}\) and \(t\) is in the \(2^{nd}\) quadrant, find \( \cos (t)\).
53) If \( \sin (t)=−\dfrac{1}{4}\) and \(t\) is in the \(3^{rd}\) quadrant, find \(\cos (t)\).
- Answer
-
\(−\dfrac{\sqrt{15}}{4}\)
54) Find the coordinates of the point on a circle with radius \(15\) corresponding to an angle of \(220°\).
55) Find the coordinates of the point on a circle with radius \(20\) corresponding to an angle of \(120°\).
- Answer
-
\((−10,10\sqrt{3})\)
56) Find the coordinates of the point on a circle with radius \(8\) corresponding to an angle of \(\dfrac{7π}{4}\).
57) Find the coordinates of the point on a circle with radius \(16\) corresponding to an angle of \(\dfrac{5π}{9}\).
- Answer
-
\((–2.778,15.757)\)
58) State the domain of the sine and cosine functions.
59) State the range of the sine and cosine functions.
- Answer
-
\([–1,1]\)
Graphical
For the exercises 60-79, use the given point on the unit circle to find the value of the sine and cosine of \(t\).
60)
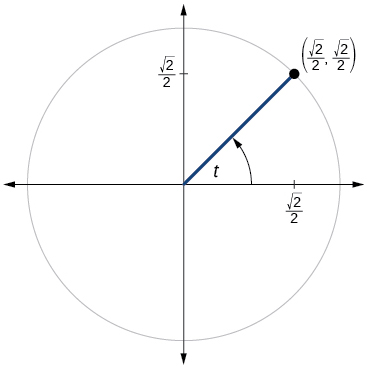
61)
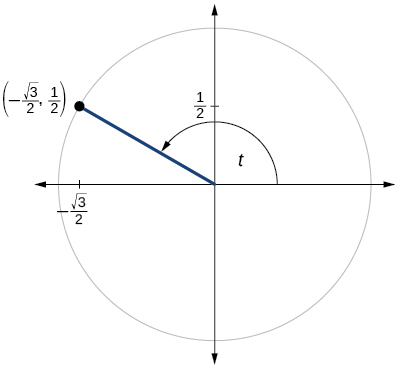
- Answer
-
\( \sin t=\dfrac{1}{2}, \cos t=−\dfrac{\sqrt{3}}{2}\)
62)
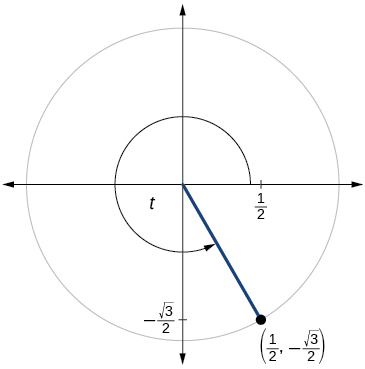
63)
- Answer
-
\( \sin t=− \dfrac{\sqrt{2}}{2}, \cos t=−\dfrac{\sqrt{2}}{2}\)
64)
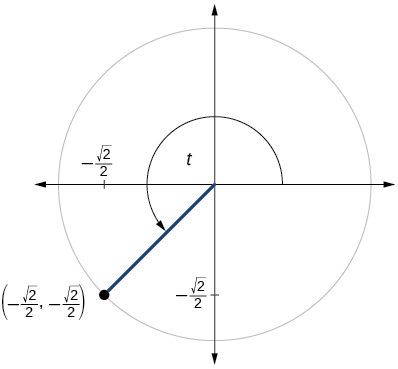
65)
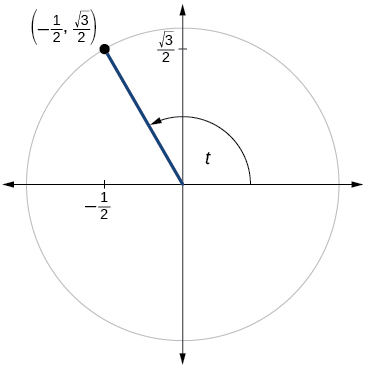
- Answer
-
\( \sin t=\dfrac{\sqrt{3}}{2},\cos t=−\dfrac{1}{2}\)
66)
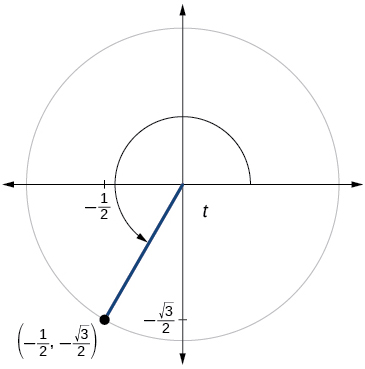
67)
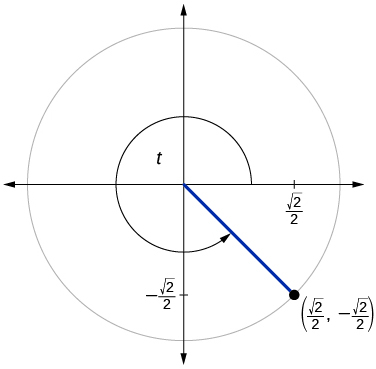
- Answer
-
\( \sin t=− \dfrac{\sqrt{2}}{2}, \cos t=\dfrac{\sqrt{2}}{2}\)
68)
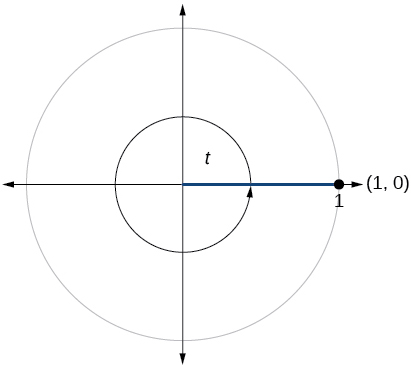
69)
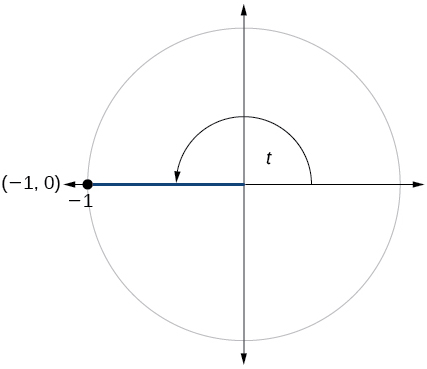
- Answer
-
\( \sin t=0, \cos t=−1\)
70)
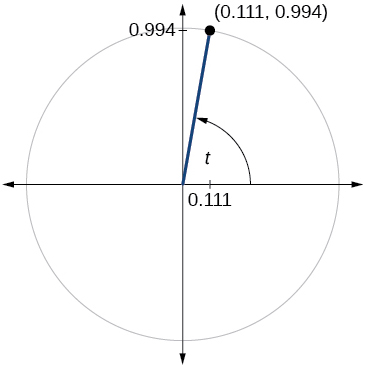
71)
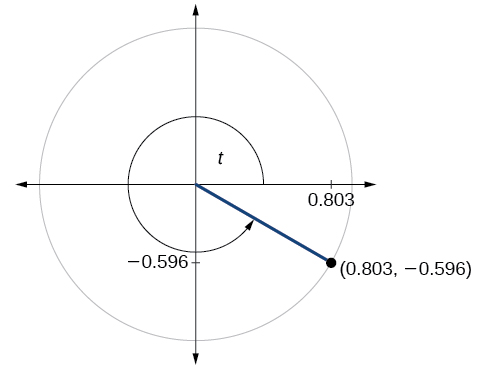
- Answer
-
\( \sin t=−0.596, \cos t=0.803\)
72)
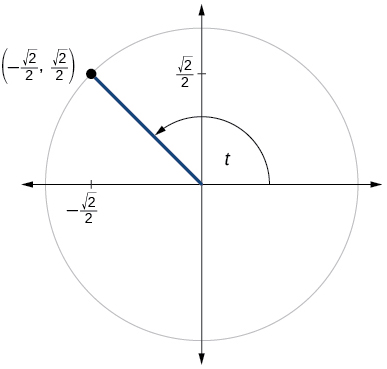
73)
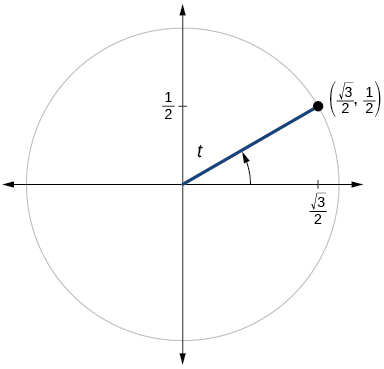
- Answer
-
\(\sin t=\dfrac{1}{2}, \cos t= \dfrac{\sqrt{3}}{2}\)
74)
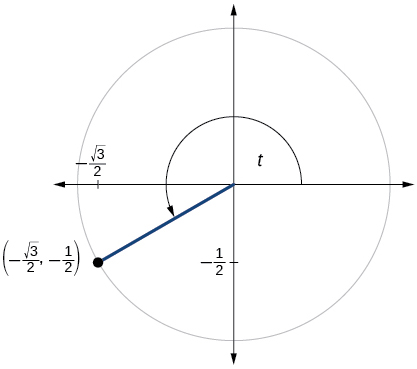
75)
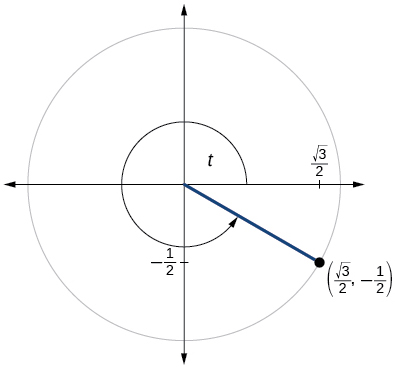
- Answer
-
\( \sin t=−\dfrac{1}{2}, \cos t= \dfrac{\sqrt{3}}{2} \)
76)
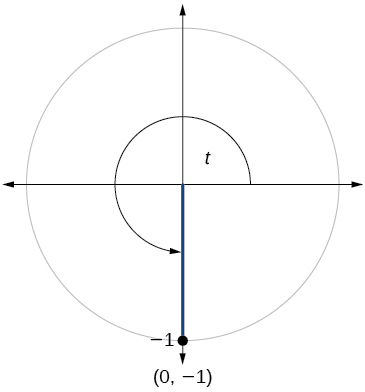
77)
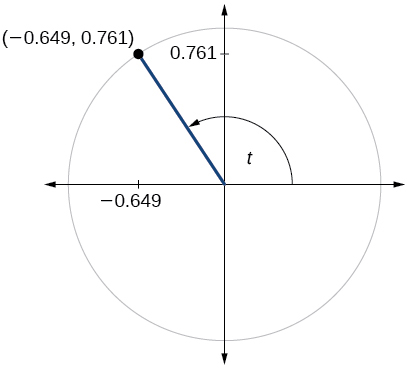
- Answer
-
\( \sin t=0.761, \cos t=−0.649 \)
78)
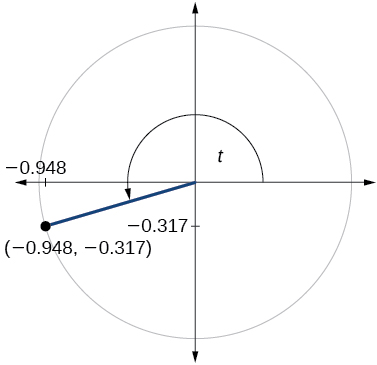
79)
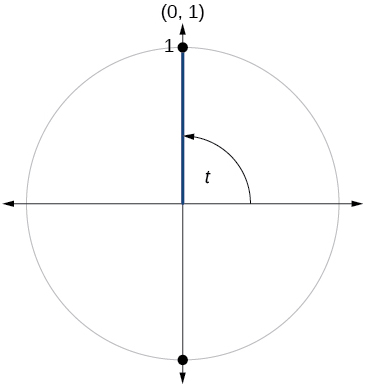
- Answer
-
\( \sin t=1, \cos t=0\)
Technology
For the exercises 80-89, use a graphing calculator to evaluate.
80) \( \sin \dfrac{5π}{9}\)
81) \(cos \dfrac{5π}{9}\)
- Answer
-
\(−0.1736\)
82) \( \sin \dfrac{π}{10}\)
83) \( \cos \dfrac{π}{10}\)
- Answer
-
\(0.9511\)
84) \( \sin \dfrac{3π}{4}\)
85) \(\cos \dfrac{3π}{4}\)
- Answer
-
\(−0.7071\)
86) \( \sin 98° \)
87) \( \cos 98° \)
- Answer
-
\(−0.1392\)
88) \( \cos 310° \)
89) \( \sin 310° \)
- Answer
-
\(−0.7660\)
Extensions
For the exercises 90-99, evaluate.
90) \( \sin \left(\dfrac{11π}{3}\right) \cos \left(\dfrac{−5π}{6}\right)\)
91) \( \sin \left(\dfrac{3π}{4}\right) \cos \left(\dfrac{5π}{3}\right) \)
- Answer
-
\(\dfrac{\sqrt{2}}{4}\)
92) \( \sin \left(− \dfrac{4π}{3}\right) \cos \left(\dfrac{π}{2}\right)\)
93) \( \sin \left(\dfrac{−9π}{4}\right) \cos \left(\dfrac{−π}{6}\right)\)
- Answer
-
\(−\dfrac{\sqrt{6}}{4}\)
94) \( \sin \left(\dfrac{π}{6}\right) \cos \left(\dfrac{−π}{3}\right) \)
95) \( \sin \left(\dfrac{7π}{4}\right) \cos \left(\dfrac{−2π}{3}\right) \)
- Answer
-
\(\dfrac{\sqrt{2}}{4}\)
96) \( \cos \left(\dfrac{5π}{6}\right) \cos \left(\dfrac{2π}{3}\right)\)
97) \( \cos \left(\dfrac{−π}{3}\right) \cos \left(\dfrac{π}{4}\right) \)
- Answer
-
\(\dfrac{\sqrt{2}}{4}\)
98) \( \sin \left(\dfrac{−5π}{4}\right) \sin \left(\dfrac{11π}{6}\right)\)
99) \( \sin (π) \sin \left(\dfrac{π}{6}\right) \)
- Answer
-
\(0\)
Real-World Applications
For the exercises 100-104, use this scenario: A child enters a carousel that takes one minute to revolve once around. The child enters at the point \((0,1)\), that is, on the due north position. Assume the carousel revolves counter clockwise.
100) What are the coordinates of the child after \(45\) seconds?
101) What are the coordinates of the child after \(90\) seconds?
- Answer
-
\((0,–1)\)
102) What is the coordinates of the child after \(125\) seconds?
103) When will the child have coordinates \((0.707,–0.707)\) if the ride lasts \(6\) minutes? (There are multiple answers.)
- Answer
-
\(37.5\) seconds, \(97.5\) seconds, \(157.5\) seconds, \(217.5\) seconds, \(277.5\) seconds, \(337.5\) seconds
104) When will the child have coordinates \((−0.866,−0.5)\) if the ride last \(6\) minutes?
5.3: The Other Trigonometric Functions
Verbal
1) On an interval of \([ 0,2π )\), can the sine and cosine values of a radian measure ever be equal? If so, where?
- Answer
-
Yes, when the reference angle is \(\dfrac{π}{4}\) and the terminal side of the angle is in quadrants I and III. Thus, at \(x=\dfrac{π}{4},\dfrac{5π}{4}\), the sine and cosine values are equal.
2) What would you estimate the cosine of \(\pi \) degrees to be? Explain your reasoning.
3) For any angle in quadrant II, if you knew the sine of the angle, how could you determine the cosine of the angle?
- Answer
-
Substitute the sine of the angle in for \(y\) in the Pythagorean Theorem \(x^2+y^2=1\). Solve for \(x\) and take the negative solution.
4) Describe the secant function.
5) Tangent and cotangent have a period of \(π\). What does this tell us about the output of these functions?
- Answer
-
The outputs of tangent and cotangent will repeat every \(π\) units.
Algebraic
For the exercises 6-17, find the exact value of each expression.
6) \( \tan \dfrac{π}{6}\)
7) \(\sec \dfrac{π}{6}\)
- Answer
-
\(\dfrac{2\sqrt{3}}{3}\)
8) \( \csc \dfrac{π}{6}\)
9) \( \cot \dfrac{π}{6}\)
- Answer
-
\(\sqrt{3}\)
10) \( \tan \dfrac{π}{4}\)
11) \( \sec \dfrac{π}{4}\)
- Answer
-
\(\sqrt{2}\)
12) \( \csc \dfrac{π}{4}\)
13) \( \cot \dfrac{π}{4}\)
- Answer
-
\(1\)
14) \( \tan \dfrac{π}{3}\)
15) \( \sec \dfrac{π}{3}\)
- Answer
-
\(2\)
16) \( \csc \dfrac{π}{3}\)
17) \( \cot \dfrac{π}{3}\)
- Answer
-
\(\dfrac{\sqrt{3}}{3}\)
For the exercises 18-48, use reference angles to evaluate the expression.
18) \( \tan \dfrac{5π}{6}\)
19) \( \sec \dfrac{7π}{6}\)
- Answer
-
\(−\dfrac{2\sqrt{3}}{3}\)
20) \( \csc \dfrac{11π}{6}\)
21) \( \cot \dfrac{13π}{6}\)
- Answer
-
\(\sqrt{3}\)
22) \( \tan \dfrac{7π}{4}\)
23) \( \sec \dfrac{3π}{4}\)
- Answer
-
\(−\sqrt{2}\)
24) \( \csc \dfrac{5π}{4}\)
25) \( \cot \dfrac{11π}{4}\)
- Answer
-
\(−1\)
26) \( \tan \dfrac{8π}{3}\)
27) \( \sec \dfrac{4π}{3}\)
- Answer
-
\(−2\)
28) \( \csc \dfrac{2π}{3}\)
29) \( \cot \dfrac{5π}{3}\)
- Answer
-
\(−\dfrac{\sqrt{3}}{3}\)
30) \( \tan 225°\)
31) \( \sec 300°\)
- Answer
-
\(2\)
32) \( \csc 150°\)
33) \( \cot 240°\)
- Answer
-
\(\dfrac{\sqrt{3}}{3}\)
34) \( \tan 330°\)
35) \( \sec 120°\)
- Answer
-
\(−2\)
36) \( \csc 210°\)
37) \( \cot 315°\)
- Answer
-
\(−1\)
38) If \( \sin t= \dfrac{3}{4}\), and \(t\) is in quadrant II, find \( \cos t, \sec t, \csc t, \tan t, \cot t \).
39) If \( \cos t=−\dfrac{1}{3},\) and \(t\) is in quadrant III, find \( \sin t, \sec t, \csc t, \tan t, \cot t\).
- Answer
-
If \(\sin t=−\dfrac{2\sqrt{2}}{3}, \sec t=−3, \csc t=−\csc t=−\dfrac{3\sqrt{2}}{4},\tan t=2\sqrt{2}, \cot t= \dfrac{\sqrt{2}}{4}\)
40) If \(\tan t=\dfrac{12}{5},\) and \(0≤t< \dfrac{π}{2}\), find \( \sin t, \cos t, \sec t, \csc t,\) and \(\cot t\).
41) If \( \sin t= \dfrac{\sqrt{3}}{2}\) and \( \cos t=\dfrac{1}{2},\) find \( \sec t, \csc t, \tan t,\) and \( \cot t\).
- Answer
-
\( \sec t=2, \csc t=\csc t=\dfrac{2\sqrt{3}}{3}, \tan t= \sqrt{3}, \cot t= \dfrac{\sqrt{3}}{3}\)
42) If \( \sin 40°≈0.643 \; \cos 40°≈0.766 \; \sec 40°,\csc 40°,\tan 40°, \text{ and } \cot 40°\).
43) If \( \sin t= \dfrac{\sqrt{2}}{2},\) what is the \( \sin (−t)\)?
- Answer
-
\(−\dfrac{\sqrt{2}}{2}\)
44) If \( \cos t= \dfrac{1}{2},\) what is the \( \cos (−t)\)?
45) If \( \sec t=3.1,\) what is the \( \sec (−t)\)?
- Answer
-
\(3.1\)
46) If \( \csc t=0.34,\) what is the \( \csc (−t)\)?
47) If \( \tan t=−1.4,\) what is the \( \tan (−t)\)?
- Answer
-
\(1.4\)
48) If \( \cot t=9.23,\) what is the \( \cot (−t)\)?
Graphical
For the exercises 49-51, use the angle in the unit circle to find the value of the each of the six trigonometric functions.
49)
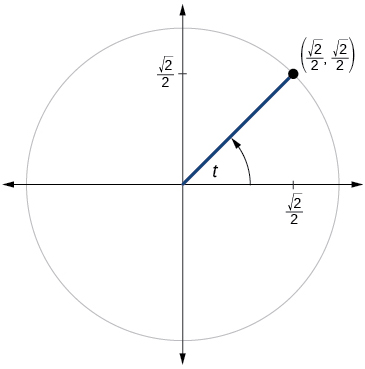
- Answer
-
\( \sin t= \dfrac{\sqrt{2}}{2}, \cos t= \dfrac{\sqrt{2}}{2}, \tan t=1,\cot t=1,\sec t= \sqrt{2}, \csc t= \csc t= \sqrt{2} \)
50)
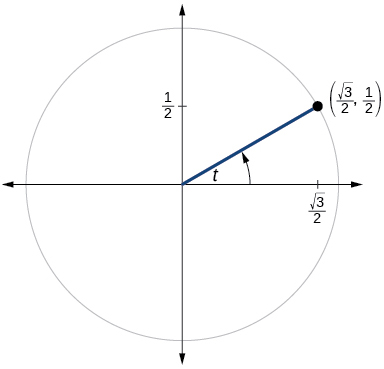
51)
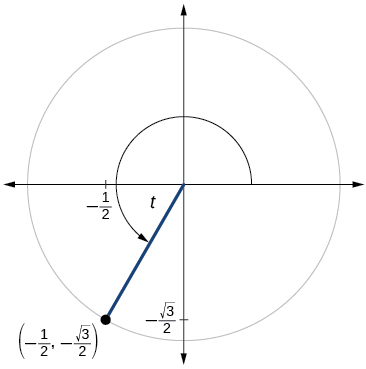
- Answer
-
\( \sin t=−\dfrac{\sqrt{3}}{2}, \cos t=−\dfrac{1}{2}, \tan t=\sqrt{3}, \cot t= \dfrac{\sqrt{3}}{3}, \sec t=−2, \csc t=−\csc t=−\dfrac{2\sqrt{3}}{3} \)
Technology
For the exercises 52-61, use a graphing calculator to evaluate.
52) \( \csc \dfrac{5π}{9}\)
53) \( \cot \dfrac{4π}{7}\)
- Answer
-
\(–0.228\)
54) \( \sec \dfrac{π}{10}\)
55) \( \tan \dfrac{5π}{8}\)
- Answer
-
\(–2.414\)
56) \( \sec \dfrac{3π}{4}\)
57) \( \csc \dfrac{π}{4}\)
- Answer
-
\(1.414\)
58) \( \tan 98°\)
59) \( \cot 33°\)
- Answer
-
\(1.540\)
60) \( \cot 140°\)
61) \( \sec 310° \)
- Answer
-
\(1.556\)
Extensions
For the exercises 62-69, use identities to evaluate the expression.
62) If \(\tan (t)≈2.7,\) and \( \sin (t)≈0.94,\) find \( \cos (t)\).
63) If \( \tan (t)≈1.3,\) and \( \cos (t)≈0.61\), find \( \sin (t)\).
- Answer
-
\( \sin (t)≈0.79 \)
64) If \( \csc (t)≈3.2,\) and \( \csc (t)≈3.2,\) and \( \cos (t)≈0.95,\) find \( \tan (t)\).
65) If \( \cot (t)≈0.58,\) and \( \cos (t)≈0.5,\) find \( \csc (t)\).
- Answer
-
\( \csc (t)≈1.16\)
66) Determine whether the function \(f(x)=2 \sin x \cos x\) is even, odd, or neither.
67) Determine whether the function \(f(x)=3 \sin ^2 x \cos x + \sec x\) is even, odd, or neither.
- Answer
-
even
68) Determine whether the function \(f(x)= \sin x −2 \cos ^2 x \) is even, odd, or neither.
69) Determine whether the function \(f(x)= \csc ^2 x+ \sec x\) is even, odd, or neither.
- Answer
-
even
For the exercises 70-71, use identities to simplify the expression.
70) \( \csc t \tan t\)
71) \( \dfrac{\sec t}{ \csc t}\)
- Answer
-
\( \dfrac{ \sin t}{ \cos t}= \tan t\)
Real-World Applications
72) The amount of sunlight in a certain city can be modeled by the function \(h=15 \cos \left(\dfrac{1}{600}d\right),\) where \(h\) represents the hours of sunlight, and \(d\) is the day of the year. Use the equation to find how many hours of sunlight there are on February 10, the \(42^{nd}\) day of the year. State the period of the function.
73) The amount of sunlight in a certain city can be modeled by the function \(h=16 \cos \left(\dfrac{1}{500}d\right)\), where \(h\) represents the hours of sunlight, and \(d\) is the day of the year. Use the equation to find how many hours of sunlight there are on September 24, the \(267^{th}\) day of the year. State the period of the function.
- Answer
-
\(13.77\) hours, period: \(1000π\)
74) The equation \(P=20 \sin (2πt)+100\) models the blood pressure, \(P\), where \(t\) represents time in seconds.
- Find the blood pressure after \(15\) seconds.
- What are the maximum and minimum blood pressures?
75) The height of a piston, \(h\), in inches, can be modeled by the equation \(y=2 \cos x+6,\) where \(x\) represents the crank angle. Find the height of the piston when the crank angle is \(55°\).
- Answer
-
\(7.73\) inches
76) The height of a piston, \(h\),in inches, can be modeled by the equation \(y=2 \cos x+5,\) where \(x\) represents the crank angle. Find the height of the piston when the crank angle is \(55°\).
5.4: Right Triangle Trigonometry
Verbal
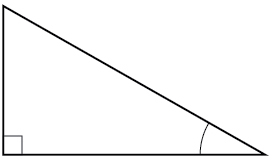
1) For the given right triangle, label the adjacent side, opposite side, and hypotenuse for the indicated angle.
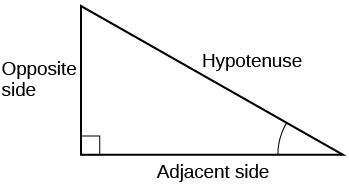
- Answer
-
2) When a right triangle with a hypotenuse of \(1\) is placed in the unit circle, which sides of the triangle correspond to the \(x\)- and \(y\)-coordinates?
3) The tangent of an angle compares which sides of the right triangle?
- Answer
-
The tangent of an angle is the ratio of the opposite side to the adjacent side.
4) What is the relationship between the two acute angles in a right triangle?
5) Explain the cofunction identity.
- Answer
-
For example, the sine of an angle is equal to the cosine of its complement; the cosine of an angle is equal to the sine of its complement.
Algebraic
For the exercises 6-9, use cofunctions of complementary angles.
6) \( \cos (34°)= \sin (\_\_°)\)
7) \( \cos (\dfrac{π}{3})= \sin (\_\_\_) \)
- Answer
-
\(\dfrac{π}{6}\)
8) \( \csc (21°) = \sec (\_\_\_°)\)
9) \( \tan (\dfrac{π}{4})= \cot (\_\_)\)
- Answer
-
\(\dfrac{π}{4}\)
For the exercises 10-16, find the lengths of the missing sides if side \(a\) is opposite angle \(A\), side \(b\) is opposite angle \(B\), and side \(c\) is the hypotenuse.
10) \( \cos B= \dfrac{4}{5},a=10\)
11) \( \sin B= \dfrac{1}{2}, a=20\)
- Answer
-
\(b= \dfrac{20\sqrt{3}}{3},c= \dfrac{40\sqrt{3}}{3}\)
12) \( \tan A= \dfrac{5}{12},b=6\)
13) \( \tan A=100,b=100\)
- Answer
-
\(a=10,000,c=10,000.5\)
14) \(\sin B=\dfrac{1}{\sqrt{3}}, a=2 \)
15) \(a=5, ∡ A=60^∘\)
- Answer
-
\(b=\dfrac{5\sqrt{3}}{3},c=\dfrac{10\sqrt{3}}{3}\)
16) \(c=12, ∡ A=45^∘\)
Graphical
For the exercises 17-22, use Figure below to evaluate each trigonometric function of angle \(A\).
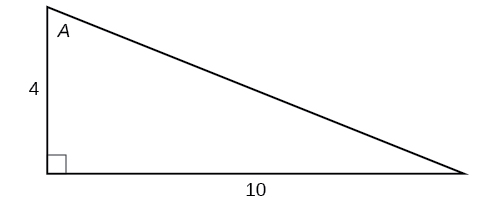
17) \(\sin A\)
- Answer
-
\(\dfrac{5\sqrt{29}}{29}\)
18) \( \cos A \)
19) \( \tan A \)
- Answer
-
\(\dfrac{5}{2}\)
20) \(\csc A \)
21) \( \sec A \)
- Answer
-
\(\dfrac{\sqrt{29}}{2}\)
22) \( \cot A \)
For the exercises 23-,28 use Figure below to evaluate each trigonometric function of angle \(A\).
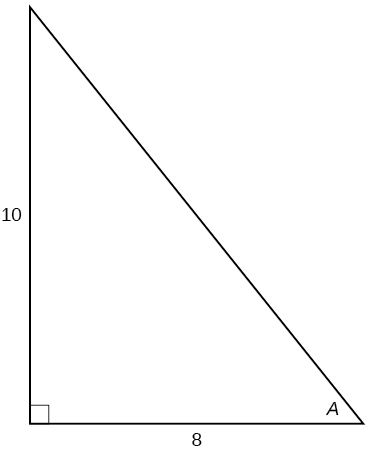
23) \( \sin A\)
- Answer
-
\(\dfrac{5\sqrt{41}}{41}\)
24) \( \cos A\)
25) \( \tan A \)
- Answer
-
\(\dfrac{5}{4}\)
26) \( \csc A\)
27) \( \sec A\)
- Answer
-
\(\dfrac{\sqrt{41}}{4}\)
28) \(\cot A\)
For the exercises 29-31, solve for the unknown sides of the given triangle.
29)
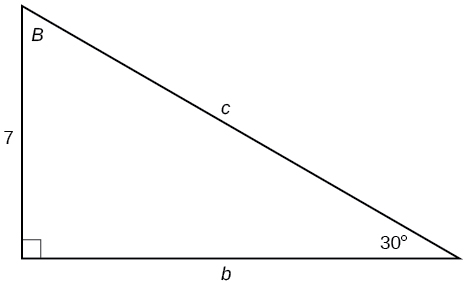
- Answer
-
\(c=14, b=7\sqrt{3}\)
30)
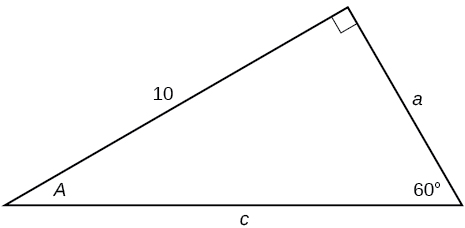
31)
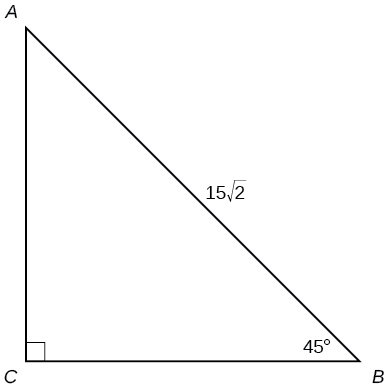
- Answer
-
\(a=15, b=15 \)
Technology
For the exercises 32-41, use a calculator to find the length of each side to four decimal places.
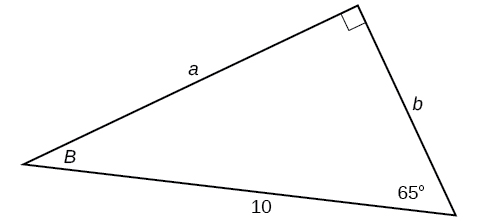
32)
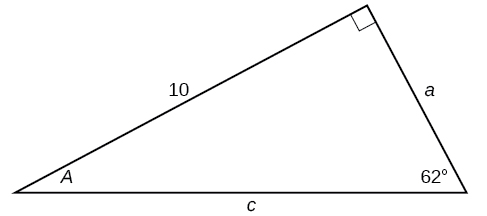
33)
- Answer
-
\(b=9.9970, c=12.2041\)
34)
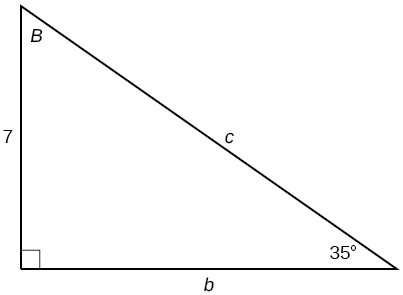
35)
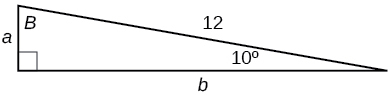
- Answer
-
\(a=2.0838, b=11.8177\)
36)
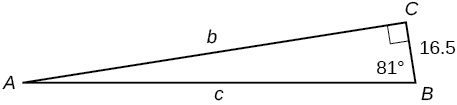
37) \(b=15, ∡B=15^∘\)
- Answer
-
\(a=55.9808,c=57.9555\)
38) \(c=200, ∡B=5^∘\)
39) \(c=50, ∡B=21^∘\)
- Answer
-
\(a=46.6790,b=17.9184\)
40) \(a=30, ∡A=27^∘\)
41) \(b=3.5, ∡A=78^∘\)
- Answer
-
\(a=16.4662,c=16.8341\)
Extensions
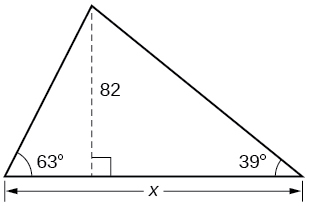
42) Find \(x\).
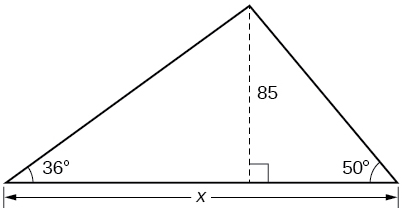
43) Find \(x\).
- Answer
-
\(188.3159\)
44) Find \(x\).
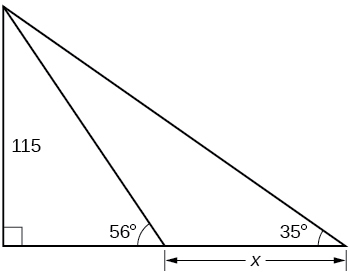
45) Find \(x\).
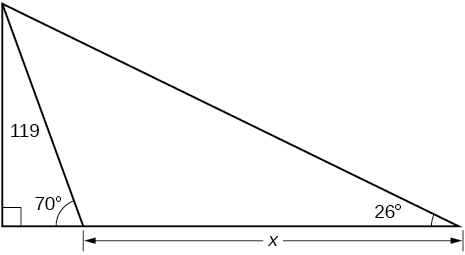
- Answer
-
\(200.6737\)
46) A radio tower is located \(400\) feet from a building. From a window in the building, a person determines that the angle of elevation to the top of the tower is \(36°\), and that the angle of depression to the bottom of the tower is \(23°\). How tall is the tower?
47) A radio tower is located \(325\) feet from a building. From a window in the building, a person determines that the angle of elevation to the top of the tower is \(43°\), and that the angle of depression to the bottom of the tower is \(31°\). How tall is the tower?
- Answer
-
\(498.3471\) ft
48) A \(200\)-foot tall monument is located in the distance. From a window in a building, a person determines that the angle of elevation to the top of the monument is \(15°\), and that the angle of depression to the bottom of the tower is \(2°\). How far is the person from the monument?
49) A \(400\)-foot tall monument is located in the distance. From a window in a building, a person determines that the angle of elevation to the top of the monument is \(18°\), and that the angle of depression to the bottom of the monument is \(3°\). How far is the person from the monument?
- Answer
-
\(1060.09\) ft
50) There is an antenna on the top of a building. From a location \(300\) feet from the base of the building, the angle of elevation to the top of the building is measured to be \(40°\). From the same location, the angle of elevation to the top of the antenna is measured to be \(43°\). Find the height of the antenna.
51) There is lightning rod on the top of a building. From a location \(500\) feet from the base of the building, the angle of elevation to the top of the building is measured to be \(36°\). From the same location, the angle of elevation to the top of the lightning rod is measured to be \(38°\). Find the height of the lightning rod.
- Answer
-
\(27.372\) ft
Real-World Applications
52) A \(33\)-ft ladder leans against a building so that the angle between the ground and the ladder is \(80°\). How high does the ladder reach up the side of the building?
53) A \(23\)-ft ladder leans against a building so that the angle between the ground and the ladder is \(80°\). How high does the ladder reach up the side of the building?
- Answer
-
\(22.6506\) ft
54) The angle of elevation to the top of a building in New York is found to be \(9\) degrees from the ground at a distance of \(1\) mile from the base of the building. Using this information, find the height of the building.
55) The angle of elevation to the top of a building in Seattle is found to be \(2\) degrees from the ground at a distance of \(2\) miles from the base of the building. Using this information, find the height of the building.
- Answer
-
\(368.7633\) ft
56) Assuming that a \(370\)-foot tall giant redwood grows vertically, if I walk a certain distance from the tree and measure the angle of elevation to the top of the tree to be \(60°\), how far from the base of the tree am I?


