10.5: Conic Sections in Polar Coordinates
- Last updated
- Save as PDF
- Page ID
- 1395
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Learning Objectives
- Identify a conic in polar form.
- Graph the polar equations of conics.
- Define conics in terms of a focus and a directrix.
Most of us are familiar with orbital motion, such as the motion of a planet around the sun or an electron around an atomic nucleus. Within the planetary system, orbits of planets, asteroids, and comets around a larger celestial body are often elliptical. Comets, however, may take on a parabolic or hyperbolic orbit instead. And, in reality, the characteristics of the planets’ orbits may vary over time. Each orbit is tied to the location of the celestial body being orbited and the distance and direction of the planet or other object from that body. As a result, we tend to use polar coordinates to represent these orbits.
In an elliptical orbit, the periapsis is the point at which the two objects are closest, and the apoapsis is the point at which they are farthest apart. Generally, the velocity of the orbiting body tends to increase as it approaches the periapsis and decrease as it approaches the apoapsis. Some objects reach an escape velocity, which results in an infinite orbit. These bodies exhibit either a parabolic or a hyperbolic orbit about a body; the orbiting body breaks free of the celestial body’s gravitational pull and fires off into space. Each of these orbits can be modeled by a conic section in the polar coordinate system.
Identifying a Conic in Polar Form
Any conic may be determined by three characteristics: a single focus, a fixed line called the directrix, and the ratio of the distances of each to a point on the graph. Consider the parabola \(x=2+y^2\) shown in Figure \(\PageIndex{2}\).
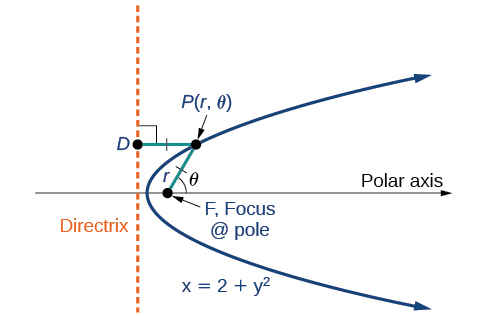
We previously learned how a parabola is defined by the focus (a fixed point) and the directrix (a fixed line). In this section, we will learn how to define any conic in the polar coordinate system in terms of a fixed point, the focus \(P(r,\theta)\) at the pole, and a line, the directrix, which is perpendicular to the polar axis.
If \(F\) is a fixed point, the focus, and \(D\) is a fixed line, the directrix, then we can let \(e\) be a fixed positive number, called the eccentricity, which we can define as the ratio of the distances from a point on the graph to the focus and the point on the graph to the directrix. Then the set of all points \(P\) such that \(e=\dfrac{PF}{PD}\) is a conic. In other words, we can define a conic as the set of all points \(P\) with the property that the ratio of the distance from \(P\) to \(F\) to the distance from \(P\) to \(D\) is equal to the constant \(e\).
For a conic with eccentricity \(e\),
- if \(0≤e<1\), the conic is an ellipse
- if \(e=1\), the conic is a parabola
- if \(e>1\), the conic is an hyperbola
With this definition, we may now define a conic in terms of the directrix, \(x=\pm p\), the eccentricity \(e\), and the angle \(\theta\). Thus, each conic may be written as a polar equation, an equation written in terms of \(r\) and \(\theta\).
THE POLAR EQUATION FOR A CONIC
For a conic with a focus at the origin, if the directrix is \(x=\pm p\), where \(p\) is a positive real number, and the eccentricity is a positive real number \(e\), the conic has a polar equation
\[r=\dfrac{ep}{1\pm e \cos \theta}\]
For a conic with a focus at the origin, if the directrix is \(y=\pm p\), where \(p\) is a positive real number, and the eccentricity is a positive real number \(e\), the conic has a polar equation
\[r=\dfrac{ep}{1\pm e \sin \theta}\]
How to: Given the polar equation for a conic, identify the type of conic, the directrix, and the eccentricity.
- Multiply the numerator and denominator by the reciprocal of the constant in the denominator to rewrite the equation in standard form.
- Identify the eccentricity \(e\) as the coefficient of the trigonometric function in the denominator.
- Compare \(e\) with \(1\) to determine the shape of the conic.
- Determine the directrix as \(x=p\) if cosine is in the denominator and \(y=p\) if sine is in the denominator. Set \(ep\) equal to the numerator in standard form to solve for \(x\) or \(y\).
Example \(\PageIndex{1}\): Identifying a Conic Given the Polar Form
For each of the following equations, identify the conic with focus at the origin, the directrix, and the eccentricity.
- \(r=\dfrac{6}{3+2 \sin \theta}\)
- \(r=\dfrac{12}{4+5 \cos \theta}\)
- \(r=\dfrac{7}{2−2 \sin \theta}\)
Solution
For each of the three conics, we will rewrite the equation in standard form. Standard form has a \(1\) as the constant in the denominator. Therefore, in all three parts, the first step will be to multiply the numerator and denominator by the reciprocal of the constant of the original equation, \(\dfrac{1}{c}\), where \(c\) is that constant.
- Multiply the numerator and denominator by \(\dfrac{1}{3}\).
\(r=\dfrac{6}{3+2\sin \theta}⋅\dfrac{\left(\dfrac{1}{3}\right)}{\left(\dfrac{1}{3}\right)}=\dfrac{6\left(\dfrac{1}{3}\right)}{3\left(\dfrac{1}{3}\right)+2\left(\dfrac{1}{3}\right)\sin \theta}=\dfrac{2}{1+\dfrac{2}{3} \sin \theta}\)
Because \(\sin \theta\) is in the denominator, the directrix is \(y=p\). Comparing to standard form, note that \(e=\dfrac{2}{3}\).Therefore, from the numerator,
\[\begin{align*} 2&=ep\\ 2&=\dfrac{2}{3}p\\ \left(\dfrac{3}{2}\right)2&=\left(\dfrac{3}{2}\right)\dfrac{2}{3}p\\ 3&=p \end{align*}\]
Since \(e<1\), the conic is an ellipse. The eccentricity is \(e=\dfrac{2}{3}\) and the directrix is \(y=3\).
- Multiply the numerator and denominator by \(\dfrac{1}{4}\).
\[\begin{align*} r&=\dfrac{12}{4+5 \cos \theta}\cdot \dfrac{\left(\dfrac{1}{4}\right)}{\left(\dfrac{1}{4}\right)}\\ r&=\dfrac{12\left(\dfrac{1}{4}\right)}{4\left(\dfrac{1}{4}\right)+5\left(\dfrac{1}{4}\right)\cos \theta}\\ r&=\dfrac{3}{1+\dfrac{5}{4} \cos \theta} \end{align*}\]
Because \(\cos \theta\) is in the denominator, the directrix is \(x=p\). Comparing to standard form, \(e=\dfrac{5}{4}\). Therefore, from the numerator,
\[\begin{align*} 3&=ep\\ 3&=\dfrac{5}{4}p\\ \left(\dfrac{4}{5}\right)3&=\left(\dfrac{4}{5}\right)\dfrac{5}{4}p\\ \dfrac{12}{5}&=p \end{align*}\]
Since \(e>1\), the conic is a hyperbola. The eccentricity is \(e=\dfrac{5}{4}\) and the directrix is \(x=\dfrac{12}{5}=2.4\).
- Multiply the numerator and denominator by \(\dfrac{1}{2}\).
\[\begin{align*} r&=\dfrac{7}{2-2 \sin \theta}\cdot \dfrac{\left(\dfrac{1}{2}\right)}{\left(\dfrac{1}{2}\right)}\\ r&=\dfrac{7\left(\dfrac{1}{2}\right)}{2\left(\dfrac{1}{2}\right)-2\left(\dfrac{1}{2}\right) \sin \theta}\\ r&=\dfrac{\dfrac{7}{2}}{1-\sin \theta} \end{align*}\]
Because sine is in the denominator, the directrix is \(y=−p\). Comparing to standard form, \(e=1\). Therefore, from the numerator,
\[\begin{align*} \dfrac{7}{2}&=ep\\ \dfrac{7}{2}&=(1)p\\ \dfrac{7}{2}&=p \end{align*}\]
Because \(e=1\), the conic is a parabola. The eccentricity is \(e=1\) and the directrix is \(y=−\dfrac{7}{2}=−3.5\).
Exercise \(\PageIndex{1}\)
Identify the conic with focus at the origin, the directrix, and the eccentricity for \(r=\dfrac{2}{3−\cos \theta}\).
- Answer
-
ellipse; \(e=\dfrac{1}{3}\); \(x=−2\)
Graphing the Polar Equations of Conics
When graphing in Cartesian coordinates, each conic section has a unique equation. This is not the case when graphing in polar coordinates. We must use the eccentricity of a conic section to determine which type of curve to graph, and then determine its specific characteristics. The first step is to rewrite the conic in standard form as we have done in the previous example. In other words, we need to rewrite the equation so that the denominator begins with \(1\). This enables us to determine \(e\) and, therefore, the shape of the curve. The next step is to substitute values for \(\theta\) and solve for \(r\) to plot a few key points. Setting \(\theta\) equal to \(0\), \(\dfrac{\pi}{2}\), \(\pi\), and \(\dfrac{3\pi}{2}\) provides the vertices so we can create a rough sketch of the graph.
Example \(\PageIndex{2A}\): Graphing a Parabola in Polar Form
Graph \(r=\dfrac{5}{3+3 \cos \theta}\).
Solution
First, we rewrite the conic in standard form by multiplying the numerator and denominator by the reciprocal of \(3\), which is \(\dfrac{1}{3}\).
\[\begin{align*} r &= \dfrac{5}{3+3 \cos \theta}=\dfrac{5\left(\dfrac{1}{3}\right)}{3\left(\dfrac{1}{3}\right)+3\left(\dfrac{1}{3}\right)\cos \theta} \\ r &= \dfrac{\dfrac{5}{3}}{1+\cos \theta} \end{align*}\]
Because \(e=1\),we will graph a parabola with a focus at the origin. The function has a \(\cos \theta\), and there is an addition sign in the denominator, so the directrix is \(x=p\).
\[\begin{align*} \dfrac{5}{3}&=ep\\ \dfrac{5}{3}&=(1)p\\ \dfrac{5}{3}&=p \end{align*}\]
The directrix is \(x=\dfrac{5}{3}\).
Plotting a few key points as in Table \(\PageIndex{1}\) will enable us to see the vertices. See Figure \(\PageIndex{3}\).
| A | B | C | D | |
|---|---|---|---|---|
| \(\theta\) | \(0\) | \(\dfrac{\pi}{2}\) | \(\pi\) | \(\dfrac{3\pi}{2}\) |
| \(r=\dfrac{5}{3+3 \cos \theta}\) | \(\dfrac{5}{6}≈0.83\) | \(\dfrac{5}{3}≈1.67\) | undefined | \(\dfrac{5}{3}≈1.67\) |
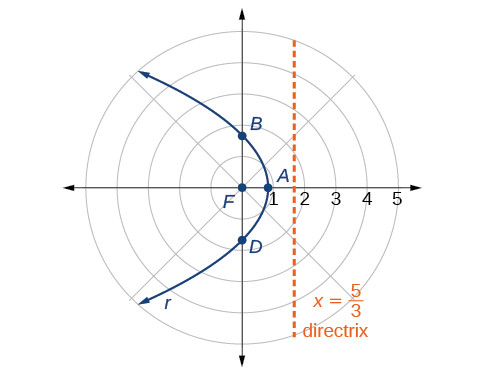
We can check our result with a graphing utility. See Figure \(\PageIndex{4}\).

Example \(\PageIndex{2B}\): Graphing a Hyperbola in Polar Form
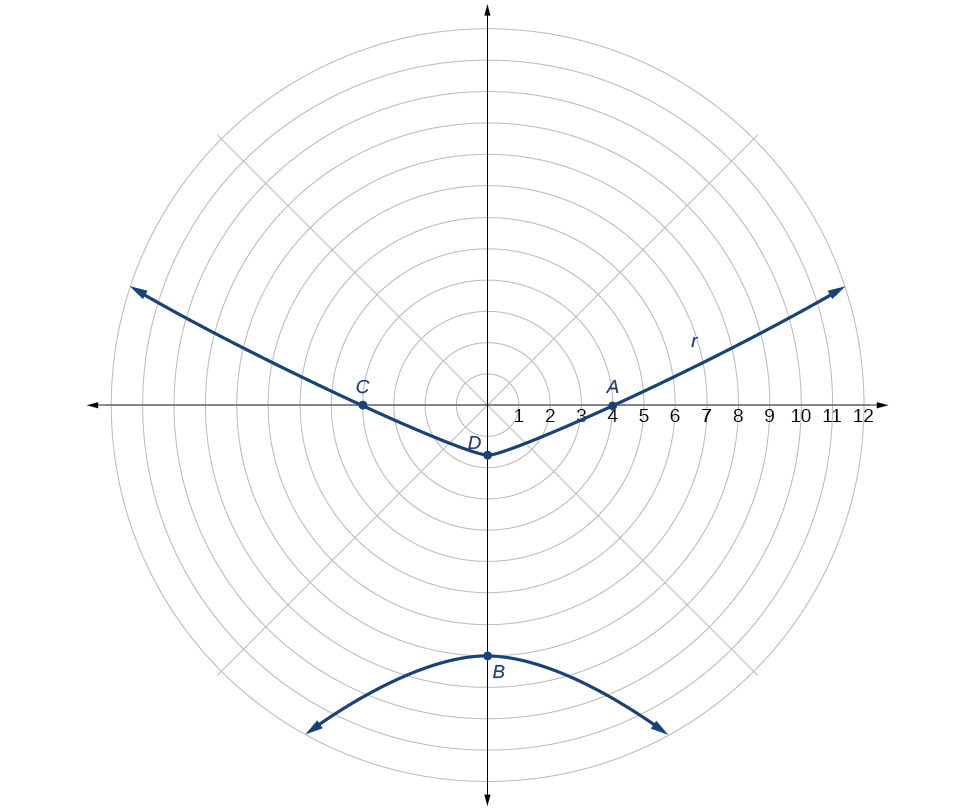
Graph \(r=\dfrac{8}{2−3 \sin \theta}\).
Solution
First, we rewrite the conic in standard form by multiplying the numerator and denominator by the reciprocal of \(2\), which is \(\dfrac{1}{2}\).
\[\begin{align*} r &=\dfrac{8}{2−3\sin \theta}=\dfrac{8\left(\dfrac{1}{2}\right)}{2\left(\dfrac{1}{2}\right)−3\left(\dfrac{1}{2}\right)\sin \theta} \\ r &= \dfrac{4}{1−\dfrac{3}{2} \sin \theta} \end{align*}\]
Because \(e=\dfrac{3}{2}\), \(e>1\), so we will graph a hyperbola with a focus at the origin. The function has a \(\sin \theta\) term and there is a subtraction sign in the denominator, so the directrix is \(y=−p\).
\[\begin{align*} 4&=ep\\ 4&=\left(\dfrac{3}{2}\right)p\\ 4\left(\dfrac{2}{3}\right)&=p\\ \dfrac{8}{3}&=p \end{align*}\]
The directrix is \(y=−\dfrac{8}{3}\).
Plotting a few key points as in Table \(\PageIndex{2}\) will enable us to see the vertices. See Figure \(\PageIndex{5}\).
| A | B | C | D | |
|---|---|---|---|---|
| \(\theta\) | \(0\) | \(\dfrac{\pi}{2}\) | \(\pi\) | \(\dfrac{3\pi}{2}\) |
| \(r=\dfrac{8}{2−3\sin \theta}\) | \(4\) | \(−8\) | \(4\) | \(\dfrac{8}{5}=1.6\) |
Example \(\PageIndex{2C}\): Graphing an Ellipse in Polar Form
Graph \(r=\dfrac{10}{5−4 \cos \theta}\).
Solution
First, we rewrite the conic in standard form by multiplying the numerator and denominator by the reciprocal of 5, which is \(\dfrac{1}{5}\).
\[\begin{align*} r &= \dfrac{10}{5−4\cos \theta}=\dfrac{10\left(\dfrac{1}{5}\right)}{5\left(\dfrac{1}{5}\right)−4\left(\dfrac{1}{5}\right)\cos \theta} \\ r &= \dfrac{2}{1−\dfrac{4}{5} \cos \theta} \end{align*}\]
Because \(e=\dfrac{4}{5}\), \(e<1\), so we will graph an ellipse with a focus at the origin. The function has a \(\cos \theta\), and there is a subtraction sign in the denominator, so the directrix is \(x=−p\).
\[\begin{align*} 2&=ep\\ 2&=\left(\dfrac{4}{5}\right)p\\ 2\left(\dfrac{5}{4}\right)&=p\\ \dfrac{5}{2}&=p \end{align*}\]
The directrix is \(x=−\dfrac{5}{2}\).
Plotting a few key points as in Table \(\PageIndex{3}\) will enable us to see the vertices. See Figure \(\PageIndex{6}\).
| A | B | C | D | |
|---|---|---|---|---|
| \(\theta\) | \(0\) | \(\dfrac{\pi}{2}\) | \(\pi\) | \(\dfrac{3\pi}{2}\) |
| \(r=\dfrac{10}{5−4 \cos \theta}\) | \(10\) | \(2\) | \(\dfrac{10}{9}≈1.1\) | \(2\) |
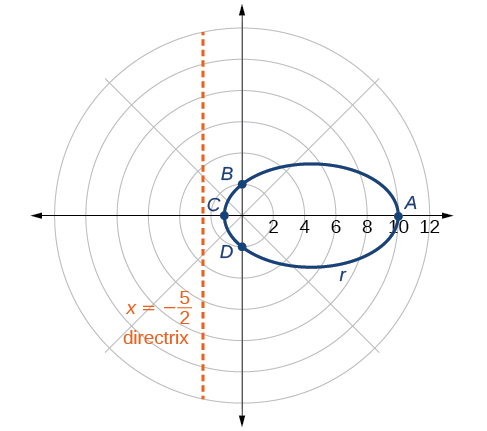
Analysis
We can check our result using a graphing utility. See Figure \(\PageIndex{7}\).
Exercise \(\PageIndex{2}\)
Graph \(r=\dfrac{2}{4−\cos \theta}\).
- Answer
-
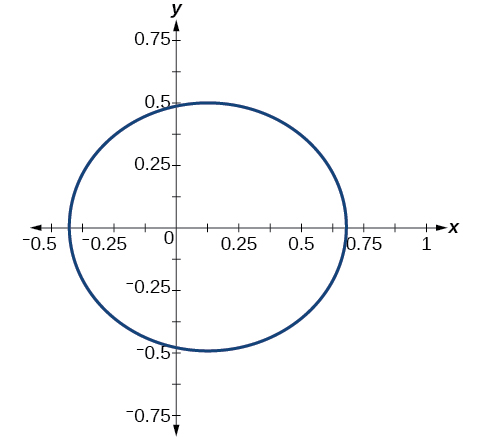
Figure \(\PageIndex{7}\)
Defining Conics in Terms of a Focus and a Directrix
So far we have been using polar equations of conics to describe and graph the curve. Now we will work in reverse; we will use information about the origin, eccentricity, and directrix to determine the polar equation.
How to: Given the focus, eccentricity, and directrix of a conic, determine the polar equation
- Determine whether the directrix is horizontal or vertical. If the directrix is given in terms of \(y\), we use the general polar form in terms of sine. If the directrix is given in terms of \(x\), we use the general polar form in terms of cosine.
- Determine the sign in the denominator. If \(p<0\), use subtraction. If \(p>0\), use addition.
- Write the coefficient of the trigonometric function as the given eccentricity.
- Write the absolute value of \(p\) in the numerator, and simplify the equation.
Example \(\PageIndex{3A}\): Finding the Polar Form of a Vertical Conic Given a Focus at the Origin and the Eccentricity and Directrix
Find the polar form of the conic given a focus at the origin, \(e=3\) and directrix \(y=−2\).
Solution
The directrix is \(y=−p\), so we know the trigonometric function in the denominator is sine.
Because \(y=−2\), \(–2<0\), so we know there is a subtraction sign in the denominator. We use the standard form of
\(r=\dfrac{ep}{1−e \sin \theta}\)
and \(e=3\) and \(|−2|=2=p\).
Therefore,
\[\begin{align*} r&=\dfrac{(3)(2)}{1-3 \sin \theta}\\ r&=\dfrac{6}{1-3 \sin \theta} \end{align*}\]
Example \(\PageIndex{3B}\): Finding the Polar Form of a Horizontal Conic Given a Focus at the Origin and the Eccentricity and Directrix
Find the polar form of a conic given a focus at the origin, \(e=\dfrac{3}{5}\), and directrix \(x=4\).
Solution
Because the directrix is \(x=p\), we know the function in the denominator is cosine. Because \(x=4\), \(4>0\), so we know there is an addition sign in the denominator. We use the standard form of
\(r=\dfrac{ep}{1+e \cos \theta}\)
and \(e=\dfrac{3}{5}\) and \(|4|=4=p\).
Therefore,
\[\begin{align*} r &= \dfrac{\left(\dfrac{3}{5}\right)(4)}{1+\dfrac{3}{5}\cos\theta} \\ r &= \dfrac{\dfrac{12}{5}}{1+\dfrac{3}{5}\cos\theta} \\ r &=\dfrac{\dfrac{12}{5}}{1\left(\dfrac{5}{5}\right)+\dfrac{3}{5}\cos\theta} \\ r &=\dfrac{\dfrac{12}{5}}{\dfrac{5}{5}+\dfrac{3}{5}\cos\theta} \\ r &= \dfrac{12}{5}⋅\dfrac{5}{5+3\cos\theta} \\ r &=\dfrac{12}{5+3\cos\theta} \end{align*}\]
Exercise \(\PageIndex{3}\)
Find the polar form of the conic given a focus at the origin, \(e=1\), and directrix \(x=−1\).
- Answer
-
\(r=\dfrac{1}{1−\cos\theta}\)
Example \(\PageIndex{4}\): Converting a Conic in Polar Form to Rectangular Form
Convert the conic \(r=\dfrac{1}{5−5\sin \theta}\) to rectangular form.
Solution
We will rearrange the formula to use the identities \(r=\sqrt{x^2+y^2}\), \(x=r \cos \theta\),and \(y=r \sin \theta\).
\[\begin{align*} r&=\dfrac{1}{5-5 \sin \theta} \\ r\cdot (5-5 \sin \theta)&=\dfrac{1}{5-5 \sin \theta}\cdot (5-5 \sin \theta)\qquad \text{Eliminate the fraction.} \\ 5r-5r \sin \theta&=1 \qquad \text{Distribute.} \\ 5r&=1+5r \sin \theta \qquad \text{Isolate }5r. \\ 25r^2&={(1+5r \sin \theta)}^2 \qquad \text{Square both sides. } \\ 25(x^2+y^2)&={(1+5y)}^2 \qquad \text{Substitute } r=\sqrt{x^2+y^2} \text{ and }y=r \sin \theta. \\ 25x^2+25y^2&=1+10y+25y^2 \qquad \text{Distribute and use FOIL. } \\ 25x^2-10y&=1 \qquad \text{Rearrange terms and set equal to 1.} \end{align*}\]
Exercise \(\PageIndex{4}\)
Convert the conic \(r=\dfrac{2}{1+2 \cos \theta}\) to rectangular form.
- Answer
-
\(4−8x+3x^2−y^2=0\)
Media
Access these online resources for additional instruction and practice with conics in polar coordinates.
- Polar Equations of Conic Sections
- Graphing Polar Equations of Conics - 1
- Graphing Polar Equations of Conics - 2
Visit this website for additional practice questions from Learningpod.
Key Concepts
- Any conic may be determined by a single focus, the corresponding eccentricity, and the directrix. We can also define a conic in terms of a fixed point, the focus \(P(r,\theta)\) at the pole, and a line, the directrix, which is perpendicular to the polar axis.
- A conic is the set of all points \(e=\dfrac{PF}{PD}\), where eccentricity \(e\) is a positive real number. Each conic may be written in terms of its polar equation. See Example \(\PageIndex{1}\).
- The polar equations of conics can be graphed. See Example \(\PageIndex{2}\), Example \(\PageIndex{3}\), and Example \(\PageIndex{4}\).
- Conics can be defined in terms of a focus, a directrix, and eccentricity. See Example \(\PageIndex{5}\) and Example \(\PageIndex{6}\).
- We can use the identities \(r=\sqrt{x^2+y^2}\), \(x=r \cos \theta\),and \(y=r \sin \theta\) to convert the equation for a conic from polar to rectangular form. See Example \(\PageIndex{7}\).


