10.2: The Hyperbola
- Last updated
- Save as PDF
- Page ID
- 1392
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Locate a hyperbola’s vertices and foci.
- Write equations of hyperbolas in standard form.
- Graph hyperbolas centered at the origin.
- Graph hyperbolas not centered at the origin.
- Solve applied problems involving hyperbolas.
What do paths of comets, supersonic booms, ancient Grecian pillars, and natural draft cooling towers have in common? They can all be modeled by the same type of conic. For instance, when something moves faster than the speed of sound, a shock wave in the form of a cone is created. A portion of a conic is formed when the wave intersects the ground, resulting in a sonic boom (Figure \(\PageIndex{1}\)).
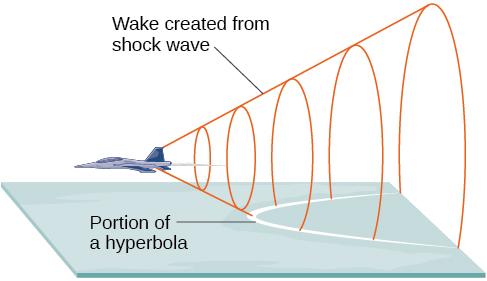
Most people are familiar with the sonic boom created by supersonic aircraft, but humans were breaking the sound barrier long before the first supersonic flight. The crack of a whip occurs because the tip is exceeding the speed of sound. The bullets shot from many firearms also break the sound barrier, although the bang of the gun usually supersedes the sound of the sonic boom.
Locating the Vertices and Foci of a Hyperbola
In analytic geometry, a hyperbola is a conic section formed by intersecting a right circular cone with a plane at an angle such that both halves of the cone are intersected. This intersection produces two separate unbounded curves that are mirror images of each other (Figure \(\PageIndex{2}\)).
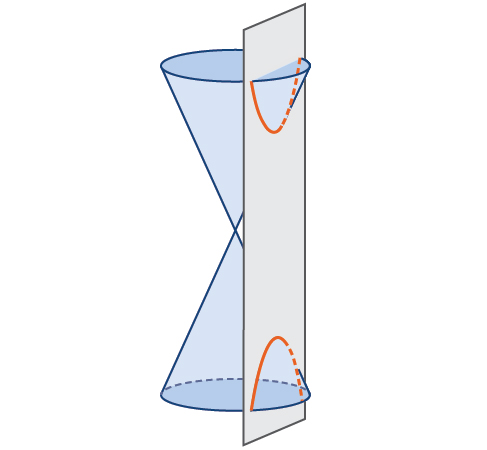
Like the ellipse, the hyperbola can also be defined as a set of points in the coordinate plane. A hyperbola is the set of all points \((x,y)\) in a plane such that the difference of the distances between \((x,y)\) and the foci is a positive constant.
Notice that the definition of a hyperbola is very similar to that of an ellipse. The distinction is that the hyperbola is defined in terms of the difference of two distances, whereas the ellipse is defined in terms of the sum of two distances.
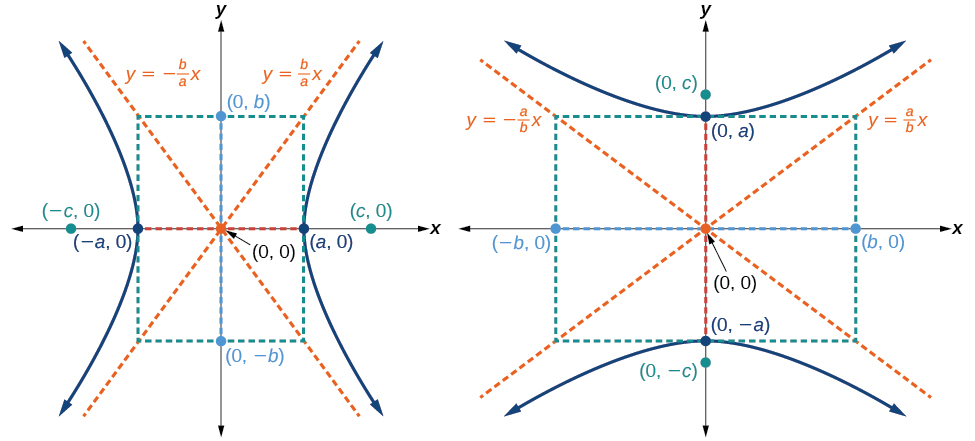
As with the ellipse, every hyperbola has two axes of symmetry. The transverse axis is a line segment that passes through the center of the hyperbola and has vertices as its endpoints. The foci lie on the line that contains the transverse axis. The conjugate axis is perpendicular to the transverse axis and has the co-vertices as its endpoints. The center of a hyperbola is the midpoint of both the transverse and conjugate axes, where they intersect. Every hyperbola also has two asymptotes that pass through its center. As a hyperbola recedes from the center, its branches approach these asymptotes. The central rectangle of the hyperbola is centered at the origin with sides that pass through each vertex and co-vertex; it is a useful tool for graphing the hyperbola and its asymptotes. To sketch the asymptotes of the hyperbola, simply sketch and extend the diagonals of the central rectangle (Figure \(\PageIndex{3}\)).
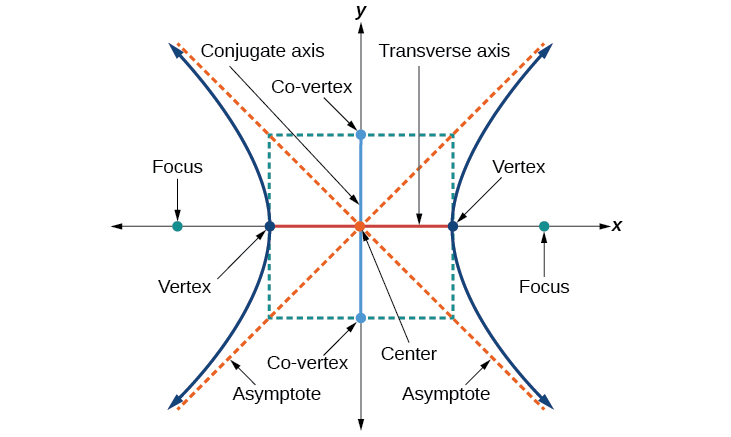
In this section, we will limit our discussion to hyperbolas that are positioned vertically or horizontally in the coordinate plane; the axes will either lie on or be parallel to the \(x\)- and \(y\)-axes. We will consider two cases: those that are centered at the origin, and those that are centered at a point other than the origin.
Deriving the Equation of an Ellipse Centered at the Origin
Let \((−c,0)\) and \((c,0)\) be the foci of a hyperbola centered at the origin. The hyperbola is the set of all points \((x,y)\) such that the difference of the distances from \((x,y)\) to the foci is constant. See Figure \(\PageIndex{4}\).
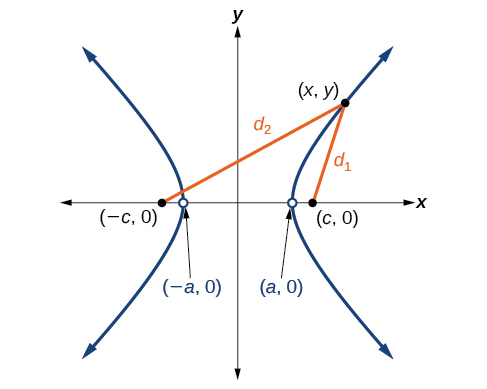
If \((a,0)\) is a vertex of the hyperbola, the distance from \((−c,0)\) to \((a,0)\) is \(a−(−c)=a+c\). The distance from \((c,0)\) to \((a,0)\) is \(c−a\). The sum of the distances from the foci to the vertex is
\((a+c)−(c−a)=2a\)
If \((x,y)\) is a point on the hyperbola, we can define the following variables:
\(d_2=\) the distance from \((−c,0)\) to \((x,y)\)
\(d_1=\) the distance from \((c,0)\) to \((x,y)\)
By definition of a hyperbola, \(d_2−d_1\) is constant for any point \((x,y)\) on the hyperbola. We know that the difference of these distances is \(2a\) for the vertex \((a,0)\). It follows that \(d_2−d_1=2a\) for any point on the hyperbola. As with the derivation of the equation of an ellipse, we will begin by applying the distance formula. The rest of the derivation is algebraic. Compare this derivation with the one from the previous section for ellipses.
\[\begin{align*} d_2-d_1&=2a\\ \sqrt{{(x-(-c))}^2+{(y-0)}^2}-\sqrt{{(x-c)}^2+{(y-0)}^2}&=2a\qquad \text{Distance Formula}\\ \sqrt{{(x+c)}^2+y^2}-\sqrt{{(x-c)}^2+y^2}&=2a\qquad \text{Simplify expressions.}\\ \sqrt{{(x+c)}^2+y^2}&=2a+\sqrt{{(x-c)}^2+y^2}\qquad \text{Move radical to opposite side.}\\ {(x+c)}^2+y^2&={(2a+\sqrt{{(x-c)}^2+y^2})}^2\qquad \text{Square both sides.}\\ x^2+2cx+c^2+y^2&=4a^2+4a\sqrt{{(x-c)}^2+y^2}+{(x-c)}^2+y^2\qquad \text{Expand the squares.}\\ x^2+2cx+c^2+y^2&=4a^2+4a\sqrt{{(x-c)}^2+y^2}+x^2-2cx+c^2+y^2\qquad \text{Expand remaining square.}\\ 2cx&=4a^2+4a\sqrt{{(x-c)}^2+y^2}-2cx\qquad \text{Combine like terms.}\\ 4cx-4a^2&=4a\sqrt{{(x-c)}^2+y^2}\qquad \text{Isolate the radical.}\\ cx-a^2&=a\sqrt{{(x-c)}^2+y^2}\qquad \text{Divide by 4.}\\ {(cx-a^2)}^2&=a^2{\left[\sqrt{{(x-c)}^2+y^2}\right]}^2\qquad \text{Square both sides.}\\ c^2x^2-2a^2cx+a^4&=a^2(x^2-2cx+c^2+y^2)\qquad \text{Expand the squares.}\\ c^2x^2-2a^2cx+a^4&=a^2x^2-2a^2cx+a^2c^2+a^2y^2\qquad \text{Distribute } a^2\\ a^4+c^2x^2&=a^2x^2+a^2c^2+a^2y^2\qquad \text{Combine like terms.}\\ c^2x^2-a^2x^2-a^2y^2&=a^2c^2-a^4\qquad \text{Rearrange terms.}\\ x^2(c^2-a^2)-a^2y^2&=a^2(c^2-a^2)\qquad \text{Factor common terms.}\\ x^2b^2-a^2y^2&=a^2b^2\qquad \text{Set } b^2=c^2−a^2\\. \dfrac{x^2b^2}{a^2b^2}-\dfrac{a^2y^2}{a^2b^2}&=\dfrac{a^2b^2}{a^2b^2}\qquad \text{Divide both sides by } a^2b^2\\ \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}&=1\\ \end{align*}\]
This equation defines a hyperbola centered at the origin with vertices \((\pm a,0)\) and co-vertices \((0,\pm b)\).
STANDARD FORMS OF THE EQUATION OF A HYPERBOLA WITH CENTER \((0,0)\)
The standard form of the equation of a hyperbola with center \((0,0)\) and transverse axis on the \(x\)-axis is
\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\)
where
- the length of the transverse axis is \(2a\)
- the coordinates of the vertices are \((\pm a,0)\)
- the length of the conjugate axis is \(2b\)
- the coordinates of the co-vertices are \((0,\pm b)\)
- the distance between the foci is \(2c\), where \(c^2=a^2+b^2\)
- the coordinates of the foci are \((\pm c,0)\)
- the equations of the asymptotes are \(y=\pm \dfrac{b}{a}x\)
See Figure \(\PageIndex{5a}\).
The standard form of the equation of a hyperbola with center \((0,0)\) and transverse axis on the \(y\)-axis is
\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\)
where
- the length of the transverse axis is \(2a\)
- the coordinates of the vertices are \((0,\pm a)\)
- the length of the conjugate axis is \(2b\)
- the coordinates of the co-vertices are \((\pm b,0)\)
- the distance between the foci is \(2c\), where \(c^2=a^2+b^2\)
- the coordinates of the foci are \((0,\pm c)\)
- the equations of the asymptotes are \(y=\pm \dfrac{a}{b}x\)
See Figure \(\PageIndex{5b}\).
Note that the vertices, co-vertices, and foci are related by the equation \(c^2=a^2+b^2\). When we are given the equation of a hyperbola, we can use this relationship to identify its vertices and foci.
How to: Given the equation of a hyperbola in standard form, locate its vertices and foci
- Determine whether the transverse axis lies on the \(x\)- or \(y\)-axis. Notice that \(a^2\) is always under the variable with the positive coefficient. So, if you set the other variable equal to zero, you can easily find the intercepts. In the case where the hyperbola is centered at the origin, the intercepts coincide with the vertices.
- If the equation has the form \(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\), then the transverse axis lies on the \(x\)-axis. The vertices are located at \((\pm a,0)\), and the foci are located at \((\pm c,0)\).
- If the equation has the form \(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\), then the transverse axis lies on the \(y\)-axis. The vertices are located at \((0,\pm a)\), and the foci are located at \((0,\pm c)\).
- Solve for \(a\) using the equation \(a=\sqrt{a^2}\).
- Solve for \(c\) using the equation \(c=\sqrt{a^2+b^2}\).
Example \(\PageIndex{1}\): Locating a Hyperbola’s Vertices and Foci
Identify the vertices and foci of the hyperbola with equation \(\dfrac{y^2}{49}−\dfrac{x^2}{32}=1\).
Solution
The equation has the form \(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\), so the transverse axis lies on the \(y\)-axis. The hyperbola is centered at the origin, so the vertices serve as the y-intercepts of the graph. To find the vertices, set \(x=0\), and solve for \(y\).
\[\begin{align*} 1&=\dfrac{y^2}{49}-\dfrac{x^2}{32}\\ 1&=\dfrac{y^2}{49}-\dfrac{0^2}{32}\\ 1&=\dfrac{y^2}{49}\\ y^2&=49\\ y&=\pm \sqrt{49}\\ &=\pm 7 \end{align*}\]
The foci are located at \((0,\pm c)\). Solving for \(c\),
\[\begin{align*} c&=\sqrt{a^2+b^2}\\ &=\sqrt{49+32}\\ &=\sqrt{81}\\ &=9 \end{align*}\]
Therefore, the vertices are located at \((0,\pm 7)\), and the foci are located at \((0,9)\).
Exercise \(\PageIndex{1}\)
Identify the vertices and foci of the hyperbola with equation \(\dfrac{x^2}{9}−\dfrac{y^2}{25}=1\).
- Answer
-
Vertices: \((\pm 3,0)\); Foci: \((\pm \sqrt{34},0)\)
Writing Equations of Hyperbolas in Standard Form
Just as with ellipses, writing the equation for a hyperbola in standard form allows us to calculate the key features: its center, vertices, co-vertices, foci, asymptotes, and the lengths and positions of the transverse and conjugate axes. Conversely, an equation for a hyperbola can be found given its key features. We begin by finding standard equations for hyperbolas centered at the origin. Then we will turn our attention to finding standard equations for hyperbolas centered at some point other than the origin.
Hyperbolas Centered at the Origin
Reviewing the standard forms given for hyperbolas centered at \((0,0)\),we see that the vertices, co-vertices, and foci are related by the equation \(c^2=a^2+b^2\). Note that this equation can also be rewritten as \(b^2=c^2−a^2\). This relationship is used to write the equation for a hyperbola when given the coordinates of its foci and vertices.
How to: Given the vertices and foci of a hyperbola centered at \((0,0)\), write its equation in standard form
- Determine whether the transverse axis lies on the \(x\)- or \(y\)-axis.
- If the given coordinates of the vertices and foci have the form \((\pm a,0)\) and \((\pm c,0)\), respectively, then the transverse axis is the \(x\)-axis. Use the standard form \(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\).
- If the given coordinates of the vertices and foci have the form \((0,\pm a)\) and \((0,\pm c)\), respectively, then the transverse axis is the \(y\)-axis. Use the standard form \(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\).
- Find \(b^2\) using the equation \(b^2=c^2−a^2\).
- Substitute the values for \(a^2\) and \(b^2\) into the standard form of the equation determined in Step 1.
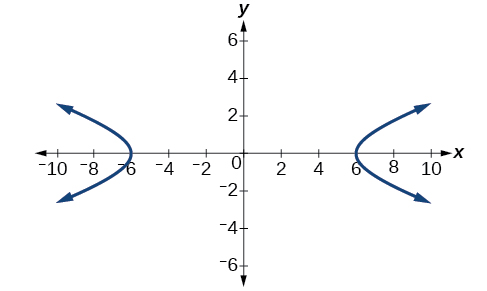
Example \(\PageIndex{2}\): Finding the Equation of a Hyperbola Centered at \((0,0)\) Given its Foci and Vertices
What is the standard form equation of the hyperbola that has vertices \((\pm 6,0)\) and foci \((\pm 2\sqrt{10},0)\)?
Solution
The vertices and foci are on the \(x\)-axis. Thus, the equation for the hyperbola will have the form \(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\).
The vertices are \((\pm 6,0)\), so \(a=6\) and \(a^2=36\).
The foci are \((\pm 2\sqrt{10},0)\), so \(c=2\sqrt{10}\) and \(c^2=40\).
Solving for \(b^2\), we have
\[\begin{align*} b^2&=c^2-a^2\\ b^2&=40-36\qquad \text{Substitute for } c^2 \text{ and } a^2\\ b^2&=4\qquad \text{Subtract.} \end{align*}\]
Finally, we substitute \(a^2=36\) and \(b^2=4\) into the standard form of the equation, \(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\). The equation of the hyperbola is \(\dfrac{x^2}{36}−\dfrac{y^2}{4}=1\), as shown in Figure \(\PageIndex{6}\).
Exercise \(\PageIndex{2}\)
What is the standard form equation of the hyperbola that has vertices \((0,\pm 2)\) and foci \((0,\pm 2\sqrt{5})\)?
- Answer
-
\(\dfrac{y^2}{4}−\dfrac{x^2}{16}=1\)
Hyperbolas Not Centered at the Origin
Like the graphs for other equations, the graph of a hyperbola can be translated. If a hyperbola is translated \(h\) units horizontally and \(k\) units vertically, the center of the hyperbola will be \((h,k)\). This translation results in the standard form of the equation we saw previously, with \(x\) replaced by \((x−h)\) and \(y\) replaced by \((y−k)\).
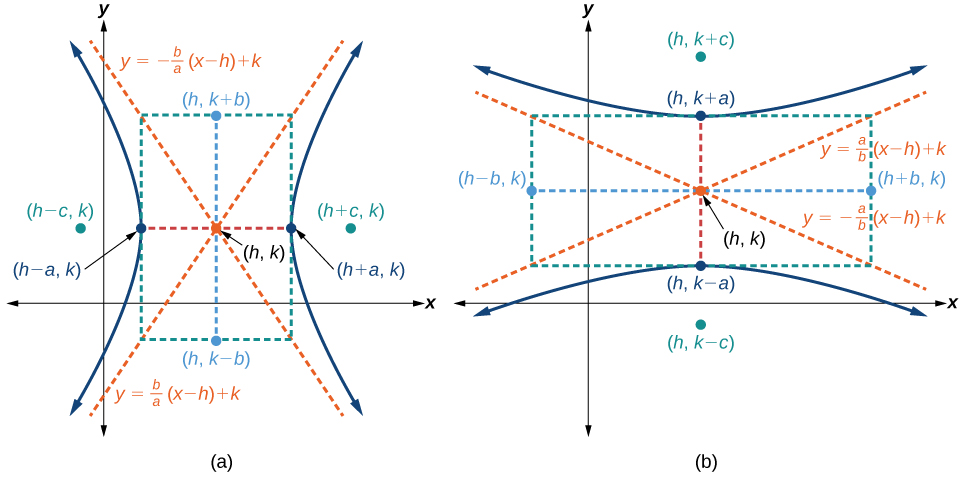
STANDARD FORMS OF THE EQUATION OF A HYPERBOLA WITH CENTER \((H, K)\)
The standard form of the equation of a hyperbola with center \((h,k)\) and transverse axis parallel to the \(x\)-axis is
\[\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\]
where
- the length of the transverse axis is \(2a\)
- the coordinates of the vertices are \((h\pm a,k)\)
- the length of the conjugate axis is \(2b\)
- the coordinates of the co-vertices are \((h,k\pm b)\)
- the distance between the foci is \(2c\), where \(c^2=a^2+b^2\)
- the coordinates of the foci are \((h\pm c,k)\)
The asymptotes of the hyperbola coincide with the diagonals of the central rectangle. The length of the rectangle is \(2a\) and its width is \(2b\). The slopes of the diagonals are \(\pm \dfrac{b}{a}\),and each diagonal passes through the center \((h,k)\). Using the point-slope formula, it is simple to show that the equations of the asymptotes are \(y=\pm \dfrac{b}{a}(x−h)+k\). See Figure \(\PageIndex{7a}\).
The standard form of the equation of a hyperbola with center \((h,k)\) and transverse axis parallel to the \(y\)-axis is
\[\dfrac{{(y−k)}^2}{a^2}−\dfrac{{(x−h)}^2}{b^2}=1\]
where
- the length of the transverse axis is \(2a\)
- the coordinates of the vertices are \((h,k\pm a)\)
- the length of the conjugate axis is \(2b\)
- the coordinates of the co-vertices are \((h\pm b,k)\)
- the distance between the foci is \(2c\), where \(c^2=a^2+b^2\)
- the coordinates of the foci are \((h,k\pm c)\)
Using the reasoning above, the equations of the asymptotes are \(y=\pm \dfrac{a}{b}(x−h)+k\). See Figure \(\PageIndex{7b}\).
Like hyperbolas centered at the origin, hyperbolas centered at a point \((h,k)\) have vertices, co-vertices, and foci that are related by the equation \(c^2=a^2+b^2\). We can use this relationship along with the midpoint and distance formulas to find the standard equation of a hyperbola when the vertices and foci are given.
How to: Given the vertices and foci of a hyperbola centered at \((h,k)\),write its equation in standard form
- Determine whether the transverse axis is parallel to the \(x\)- or \(y\)-axis.
- If the \(y\)-coordinates of the given vertices and foci are the same, then the transverse axis is parallel to the \(x\)-axis. Use the standard form \(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\).
- If the \(x\)-coordinates of the given vertices and foci are the same, then the transverse axis is parallel to the \(y\)-axis. Use the standard form \(\dfrac{{(y−k)}^2}{a^2}−\dfrac{{(x−h)}^2}{b^2}=1\).
- Identify the center of the hyperbola, \((h,k)\),using the midpoint formula and the given coordinates for the vertices.
- Find \(a^2\) by solving for the length of the transverse axis, \(2a\), which is the distance between the given vertices.
- Find \(c^2\) using \(h\) and \(k\) found in Step 2 along with the given coordinates for the foci.
- Solve for \(b^2\) using the equation \(b^2=c^2−a^2\).
- Substitute the values for \(h\), \(k\), \(a^2\), and \(b^2\) into the standard form of the equation determined in Step 1.
Example \(\PageIndex{3}\): Finding the Equation of a Hyperbola Centered at \((h, k)\) Given its Foci and Vertices
What is the standard form equation of the hyperbola that has vertices at \((0,−2)\) and \((6,−2)\) and foci at \((−2,−2)\) and \((8,−2)\)?
Solution
The \(y\)-coordinates of the vertices and foci are the same, so the transverse axis is parallel to the \(x\)-axis. Thus, the equation of the hyperbola will have the form
\(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\)
First, we identify the center, \((h,k)\). The center is halfway between the vertices \((0,−2)\) and \((6,−2)\). Applying the midpoint formula, we have
\((h,k)=(\dfrac{0+6}{2},\dfrac{−2+(−2)}{2})=(3,−2)\)
Next, we find \(a^2\). The length of the transverse axis, \(2a\),is bounded by the vertices. So, we can find \(a^2\) by finding the distance between the \(x\)-coordinates of the vertices.
\[\begin{align*} 2a&=| 0-6 |\\ 2a&=6\\ a&=3\\ a^2&=9 \end{align*}\]
Now we need to find \(c^2\). The coordinates of the foci are \((h\pm c,k)\). So \((h−c,k)=(−2,−2)\) and \((h+c,k)=(8,−2)\). We can use the \(x\)-coordinate from either of these points to solve for \(c\). Using the point \((8,−2)\), and substituting \(h=3\),
\[\begin{align*} h+c&=8\\ 3+c&=8\\ c&=5\\ c^2&=25 \end{align*}\]
Next, solve for \(b^2\) using the equation \(b^2=c^2−a^2\):
\[\begin{align*} b^2&=c^2-a^2\\ &=25-9\\ &=16 \end{align*}\]
Finally, substitute the values found for \(h\), \(k\), \(a^2\),and \(b^2\) into the standard form of the equation.
\(\dfrac{{(x−3)}^2}{9}−\dfrac{{(y+2)}^2}{16}=1\)
Exercise \(\PageIndex{3}\)
What is the standard form equation of the hyperbola that has vertices \((1,−2)\) and \((1,8)\) and foci \((1,−10)\) and \((1,16)\)?
- Answer
-
\(\dfrac{{(y−3)}^2}{25}+\dfrac{{(x−1)}^2}{144}=1\)
Graphing Hyperbolas Centered at the Origin
When we have an equation in standard form for a hyperbola centered at the origin, we can interpret its parts to identify the key features of its graph: the center, vertices, co-vertices, asymptotes, foci, and lengths and positions of the transverse and conjugate axes. To graph hyperbolas centered at the origin, we use the standard form \(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\) for horizontal hyperbolas and the standard form \(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\) for vertical hyperbolas.
How to: Given a standard form equation for a hyperbola centered at \((0,0)\), sketch the graph
- Determine which of the standard forms applies to the given equation.
- Use the standard form identified in Step 1 to determine the position of the transverse axis; coordinates for the vertices, co-vertices, and foci; and the equations for the asymptotes.
- If the equation is in the form \(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\), then
- the transverse axis is on the \(x\)-axis
- the coordinates of the vertices are \((\pm a,0)\0
- the coordinates of the co-vertices are \((0,\pm b)\)
- the coordinates of the foci are \((\pm c,0)\)
- the equations of the asymptotes are \(y=\pm \dfrac{b}{a}x\)
- If the equation is in the form \(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\), then
- the transverse axis is on the \(y\)-axis
- the coordinates of the vertices are \((0,\pm a)\)
- the coordinates of the co-vertices are \((\pm b,0)\)
- the coordinates of the foci are \((0,\pm c)\)
- the equations of the asymptotes are \(y=\pm \dfrac{a}{b}x\)
- If the equation is in the form \(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\), then
- Solve for the coordinates of the foci using the equation \(c=\pm \sqrt{a^2+b^2}\).
- Plot the vertices, co-vertices, foci, and asymptotes in the coordinate plane, and draw a smooth curve to form the hyperbola.
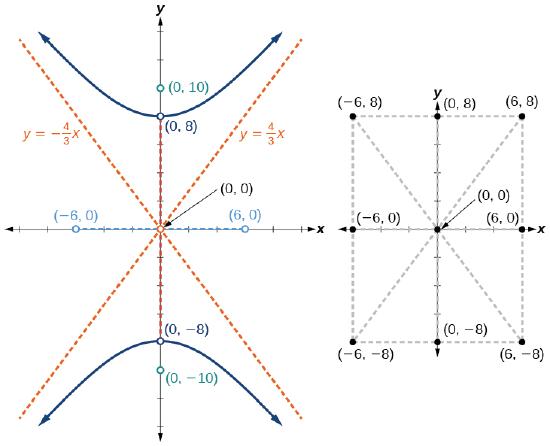
Example \(\PageIndex{4}\): Graphing a Hyperbola Centered at \((0,0)\) Given an Equation in Standard Form
Graph the hyperbola given by the equation \(\dfrac{y^2}{64}−\dfrac{x^2}{36}=1\). Identify and label the vertices, co-vertices, foci, and asymptotes.
Solution
The standard form that applies to the given equation is \(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\). Thus, the transverse axis is on the \(y\)-axis
The coordinates of the vertices are \((0,\pm a)=(0,\pm \sqrt{64})=(0,\pm 8)\)
The coordinates of the co-vertices are \((\pm b,0)=(\pm \sqrt{36}, 0)=(\pm 6,0)\)
The coordinates of the foci are \((0,\pm c)\), where \(c=\pm \sqrt{a^2+b^2}\). Solving for \(c\), we have
\(c=\pm \sqrt{a^2+b^2}=\pm \sqrt{64+36}=\pm \sqrt{100}=\pm 10\)
Therefore, the coordinates of the foci are \((0,\pm 10)\)
The equations of the asymptotes are \(y=\pm \dfrac{a}{b}x=\pm \dfrac{8}{6}x=\pm \dfrac{4}{3}x\)
Plot and label the vertices and co-vertices, and then sketch the central rectangle. Sides of the rectangle are parallel to the axes and pass through the vertices and co-vertices. Sketch and extend the diagonals of the central rectangle to show the asymptotes. The central rectangle and asymptotes provide the framework needed to sketch an accurate graph of the hyperbola. Label the foci and asymptotes, and draw a smooth curve to form the hyperbola, as shown in Figure \(\PageIndex{8}\).
Exercise \(\PageIndex{4}\)
Graph the hyperbola given by the equation \(\dfrac{x^2}{144}−\dfrac{y^2}{81}=1\). Identify and label the vertices, co-vertices, foci, and asymptotes.
- Answer
-
vertices: \((\pm 12,0)\); co-vertices: \((0,\pm 9)\); foci: \((\pm 15,0)\); asymptotes: \(y=\pm \dfrac{3}{4}x\);
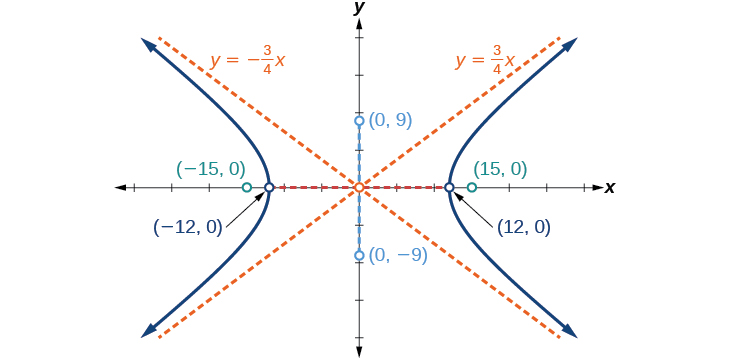
Figure \(\PageIndex{9}\)
Graphing Hyperbolas Not Centered at the Origin
Graphing hyperbolas centered at a point \((h,k)\) other than the origin is similar to graphing ellipses centered at a point other than the origin. We use the standard forms \(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\) for horizontal hyperbolas, and \(\dfrac{{(y−k)}^2}{a^2}−\dfrac{{(x−h)}^2}{b^2}=1\) for vertical hyperbolas. From these standard form equations we can easily calculate and plot key features of the graph: the coordinates of its center, vertices, co-vertices, and foci; the equations of its asymptotes; and the positions of the transverse and conjugate axes.
How to: Given a general form for a hyperbola centered at \((h, k)\), sketch the graph
- Convert the general form to that standard form. Determine which of the standard forms applies to the given equation.
- Use the standard form identified in Step 1 to determine the position of the transverse axis; coordinates for the center, vertices, co-vertices, foci; and equations for the asymptotes.
- If the equation is in the form \(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\), then
- the transverse axis is parallel to the \(x\)-axis
- the center is \((h,k)\)
- the coordinates of the vertices are \((h\pm a,k)\)
- the coordinates of the co-vertices are \((h,k\pm b)\)
- the coordinates of the foci are \((h\pm c,k)\)
- the equations of the asymptotes are \(y=\pm \dfrac{b}{a}(x−h)+k\)
- If the equation is in the form \(\dfrac{{(y−k)}^2}{a^2}−\dfrac{{(x−h)}^2}{b^2}=1\), then
- the transverse axis is parallel to the \(y\)-axis
- the center is \((h,k)\)
- the coordinates of the vertices are \((h,k\pm a)\)
- the coordinates of the co-vertices are \((h\pm b,k)\)
- the coordinates of the foci are \((h,k\pm c)\)
- the equations of the asymptotes are \(y=\pm \dfrac{a}{b}(x−h)+k\)
- If the equation is in the form \(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\), then
- Solve for the coordinates of the foci using the equation \(c=\pm \sqrt{a^2+b^2}\).
- Plot the center, vertices, co-vertices, foci, and asymptotes in the coordinate plane and draw a smooth curve to form the hyperbola.
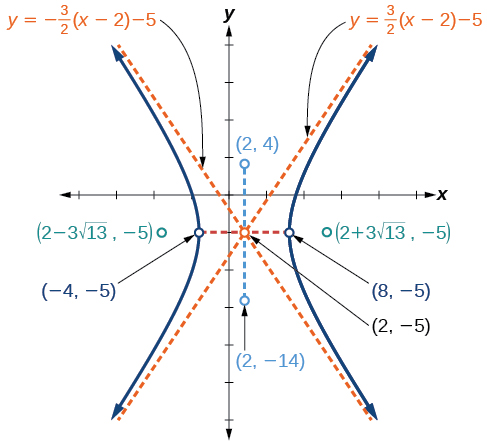
Example \(\PageIndex{5}\): Graphing a Hyperbola Centered at \((h, k)\) Given an Equation in General Form
Graph the hyperbola given by the equation \(9x^2−4y^2−36x−40y−388=0\). Identify and label the center, vertices, co-vertices, foci, and asymptotes.
Solution
Start by expressing the equation in standard form. Group terms that contain the same variable, and move the constant to the opposite side of the equation.
\((9x^2−36x)−(4y^2+40y)=388\)
Factor the leading coefficient of each expression.
\(9(x^2−4x)−4(y^2+10y)=388\)
Complete the square twice. Remember to balance the equation by adding the same constants to each side.
\(9(x^2−4x+4)−4(y^2+10y+25)=388+36−100\)
Rewrite as perfect squares.
\(9{(x−2)}^2−4{(y+5)}^2=324\)
Divide both sides by the constant term to place the equation in standard form.
\(\dfrac{{(x−2)}^2}{36}−\dfrac{{(y+5)}^2}{81}=1\)
The standard form that applies to the given equation is \(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\), where \(a^2=36\) and \(b^2=81\),or \(a=6\) and \(b=9\). Thus, the transverse axis is parallel to the \(x\)-axis. It follows that:
the center of the ellipse is \((h,k)=(2,−5)\)
the coordinates of the vertices are \((h\pm a,k)=(2\pm 6,−5)\), or \((−4,−5)\) and \((8,−5)\)
the coordinates of the co-vertices are \((h,k\pm b)=(2,−5\pm 9)\), or \((2,−14)\) and \((2,4)\)
the coordinates of the foci are \((h\pm c,k)\), where \(c=\pm \sqrt{a^2+b^2}\). Solving for \(c\),we have
\(c=\pm \sqrt{36+81}=\pm \sqrt{117}=\pm 3\sqrt{13}\)
Therefore, the coordinates of the foci are \((2−3\sqrt{13},−5)\) and \((2+3\sqrt{13},−5)\).
The equations of the asymptotes are \(y=\pm \dfrac{b}{a}(x−h)+k=\pm \dfrac{3}{2}(x−2)−5\).
Next, we plot and label the center, vertices, co-vertices, foci, and asymptotes and draw smooth curves to form the hyperbola, as shown in Figure \(\PageIndex{10}\).
Exercise \(\PageIndex{5}\)
Graph the hyperbola given by the standard form of an equation \(\dfrac{{(y+4)}^2}{100}−\dfrac{{(x−3)}^2}{64}=1\). Identify and label the center, vertices, co-vertices, foci, and asymptotes.
- Answer
-
center: \((3,−4)\); vertices: \((3,−14)\) and \((3,6)\); co-vertices: \((−5,−4)\); and \((11,−4)\); foci: \((3,−4−2\sqrt{41})\) and \((3,−4+2\sqrt{41})\); asymptotes: \(y=\pm \dfrac{5}{4}(x−3)−4\)
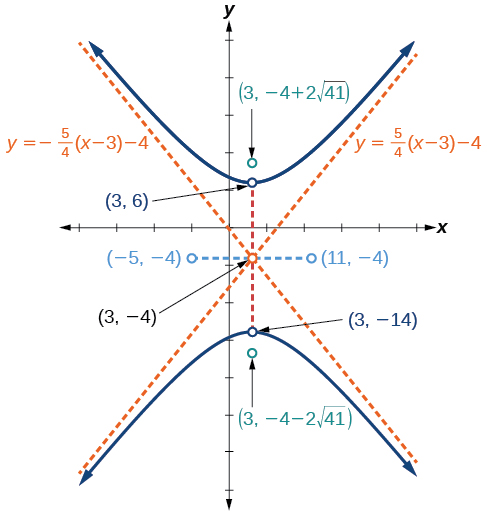
Figure \(\PageIndex{11}\)
Solving Applied Problems Involving Hyperbolas
As we discussed at the beginning of this section, hyperbolas have real-world applications in many fields, such as astronomy, physics, engineering, and architecture. The design efficiency of hyperbolic cooling towers is particularly interesting. Cooling towers are used to transfer waste heat to the atmosphere and are often touted for their ability to generate power efficiently. Because of their hyperbolic form, these structures are able to withstand extreme winds while requiring less material than any other forms of their size and strength (Figure \(\PageIndex{12}\)). For example, a \(500\)-foot tower can be made of a reinforced concrete shell only \(6\) or \(8\) inches wide!

The first hyperbolic towers were designed in 1914 and were \(35\) meters high. Today, the tallest cooling towers are in France, standing a remarkable \(170\) meters tall. In Example \(\PageIndex{6}\) we will use the design layout of a cooling tower to find a hyperbolic equation that models its sides.
Example \(\PageIndex{6}\): Solving Applied Problems Involving Hyperbolas
The design layout of a cooling tower is shown in Figure \(\PageIndex{13}\). The tower stands \(179.6\) meters tall. The diameter of the top is \(72\) meters. At their closest, the sides of the tower are \(60\) meters apart.
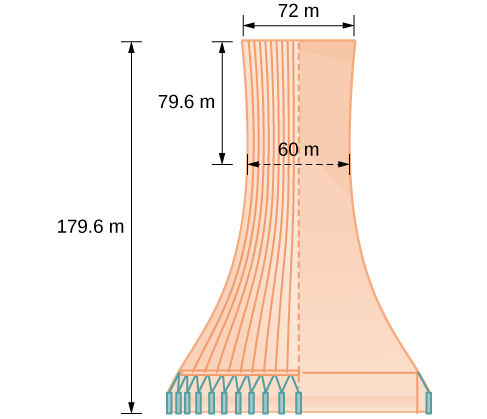
Find the equation of the hyperbola that models the sides of the cooling tower. Assume that the center of the hyperbola—indicated by the intersection of dashed perpendicular lines in the figure—is the origin of the coordinate plane. Round final values to four decimal places.
Solution
We are assuming the center of the tower is at the origin, so we can use the standard form of a horizontal hyperbola centered at the origin: \(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\), where the branches of the hyperbola form the sides of the cooling tower. We must find the values of \(a^2\) and \(b^2\) to complete the model.
First, we find \(a^2\). Recall that the length of the transverse axis of a hyperbola is \(2a\). This length is represented by the distance where the sides are closest, which is given as \(65.3\) meters. So, \(2a=60\). Therefore, \(a=30\) and \(a^2=900\).
To solve for \(b^2\),we need to substitute for \(x\) and \(y\) in our equation using a known point. To do this, we can use the dimensions of the tower to find some point \((x,y)\) that lies on the hyperbola. We will use the top right corner of the tower to represent that point. Since the \(y\)-axis bisects the tower, our \(x\)-value can be represented by the radius of the top, or \(36\) meters. The y-value is represented by the distance from the origin to the top, which is given as \(79.6\) meters. Therefore,
\[\begin{align*} \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}&=1\qquad \text{Standard form of horizontal hyperbola.}\\ b^2&=\dfrac{y^2}{\dfrac{x^2}{a^2}-1}\qquad \text{Isolate } b^2\\ &=\dfrac{{(79.6)}^2}{\dfrac{{(36)}^2}{900}-1}\qquad \text{Substitute for } a^2,\: x, \text{ and } y\\ &\approx 14400.3636\qquad \text{Round to four decimal places} \end{align*}\]
The sides of the tower can be modeled by the hyperbolic equation
\(\dfrac{x^2}{900}−\dfrac{y^2}{14400.3636}=1\),or \(\dfrac{x^2}{{30}^2}−\dfrac{y^2}{{120.0015}^2}=1\)
Exercise \(\PageIndex{6}\)
A design for a cooling tower project is shown in Figure \(\PageIndex{14}\). Find the equation of the hyperbola that models the sides of the cooling tower. Assume that the center of the hyperbola—indicated by the intersection of dashed perpendicular lines in the figure—is the origin of the coordinate plane. Round final values to four decimal places.
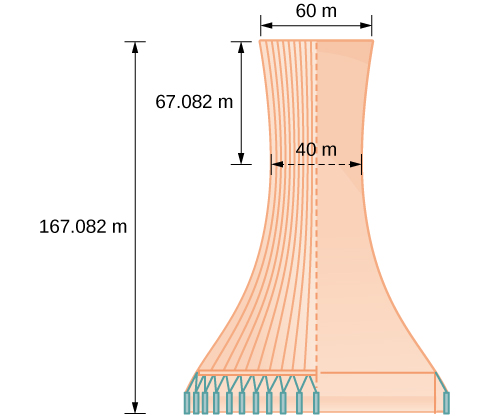
- Answer
-
The sides of the tower can be modeled by the hyperbolic equation. \(\dfrac{x^2}{400}−\dfrac{y^2}{3600}=1\) or \(\dfrac{x^2}{{20}^2}−\dfrac{y^2}{{60}^2}=1\).
Media
Access these online resources for additional instruction and practice with hyperbolas.
- Conic Sections: The Hyperbola Part 1 of 2
- Conic Sections: The Hyperbola Part 2 of 2
- Graph a Hyperbola with Center at Origin
- Graph a Hyperbola with Center not at Origin
Key Equations
| Hyperbola, center at origin, transverse axis on x-axis | \(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\) |
| Hyperbola, center at origin, transverse axis on y-axis | \(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\) |
| Hyperbola, center at \((h,k)\),transverse axis parallel to x-axis | \(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\) |
| Hyperbola, center at \((h,k)\),transverse axis parallel to y-axis | \(\dfrac{{(y−k)}^2}{a^2}−\dfrac{{(x−h)}^2}{b^2}=1\) |
Key Concepts
- A hyperbola is the set of all points \((x,y)\) in a plane such that the difference of the distances between \((x,y)\) and the foci is a positive constant.
- The standard form of a hyperbola can be used to locate its vertices and foci. See Example \(\PageIndex{1}\).
- When given the coordinates of the foci and vertices of a hyperbola, we can write the equation of the hyperbola in standard form. See Example \(\PageIndex{2}\) and Example \(\PageIndex{3}\).
- When given an equation for a hyperbola, we can identify its vertices, co-vertices, foci, asymptotes, and lengths and positions of the transverse and conjugate axes in order to graph the hyperbola. See Example \(\PageIndex{4}\) and Example \(\PageIndex{5}\).
- Real-world situations can be modeled using the standard equations of hyperbolas. For instance, given the dimensions of a natural draft cooling tower, we can find a hyperbolic equation that models its sides. See Example \(\PageIndex{6}\).


