1.05: Floating-Point Binary Representation of Numbers
- Page ID
- 126384
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lesson 1: Floating-Point Representation Background
Learning Objectives
After successful completion of this lesson, you should be able to:
1) revisit floating-point (scientific) representation for base-10 numbers
2) define mantissa, exponent, and base of a base-10 floating-point number
3) find the range of numbers that can be represented in fixed-point and floating-point format
4) identify that absolute true errors in representing numbers are bounded for the fixed format, while absolute relative true errors in representing numbers are bounded for floating-point format.
Introduction
To understand the floating-point representation advantages over fixed-point format in binary representation, we will discuss the base-\(10\) format first.
Fixed point representation
Fixed-point representation has a fixed number of places for the integer part and a fixed number of places for the fractional part. Take this as an example of fixed-point representation. Consider an old-time cash register that has three places for dollars (integer part) and two places for the cents (fractional part). One could ring purchases between \(0\) and \(999.99\) units of money. To keep it simple, we are not choosing negative numbers. Note that there are five (not six) working spaces in the cash register (the decimal number is shown just for clarification).
How will the smallest number 0 be represented?
The number \(0\) will be represented as \(000.00\)
How will the largest number 999.99 be represented?
The number \(999.99\) will be represented as \(999.99\)
Now, look at any typical number between 0 and 999.99, say, 256.78. How would it be represented?
The number \(256.78\) will be represented as \(256.78\)
What is the smallest difference between two exactly represented consecutive numbers?
The difference is always \(0.01\). For example, the difference between the consecutive numbers that can be represented exactly, say \(256.78\) and \(256.79\), is \(0.01\). This difference is the same for every two consecutive numbers.
What amount would one pay for an item if it costs 256.789?
Depending on what method you use for rounding, the amount one would pay would be \(256.79\) if the number is rounded or \(256.78\) if the number is chopped.
What true errors would occur in a transaction?
No matter what transaction is completed on the above cash register, the maximum magnitude of the true error in the payment would be less than \(0.01\) if chopping is used and less than \(0.05\) if rounding is used.
What relative errors would occur in a transaction?
The magnitude of relative true errors for representing small numbers is going to be high, while for large numbers, the magnitude of the relative true error is going to be small. Let’s illustrate that by choosing several different numbers. We will assume that we are using chopping.
For example, for \(256.786\), chopping would make it \(256.78\) and account for a round-off error of \(256.786 - 256.78 = 0.006\). The relative true error in this case is
\[\begin{split} \varepsilon_{t} &= \frac{0.006}{256.786} \\ &= 0.000023366. \end{split} \nonumber\]
For another number, \(3.546\), chopping would make it \(3.54\) and account for the round-off error of \(3.546 - 3.54 = 0.006\). However, the relative true error in this case is
\[\begin{split} \varepsilon_{t} &= \frac{0.006}{3.546}\\ &= 0.0016920 \end{split} \nonumber\]
For another number \(0.016\), chopping would make it \(0.01\) and account for the round-off error of \(0.016 - 0.01 = 0.006\). However, the relative true error in this case is
\[\begin{split} \varepsilon_{t} &= \frac{0.006}{0.016} \\ &= 0.375. \end{split} \nonumber\]
From the above examples, we see that when we used fixed point (also called decimal for base-\(10\)) format like in the cash register, we have control over the magnitude of the true error but not the magnitude of the relative true error.
The magnitude of the true error for any number that can be represented in the above configuration of three places for the integer part and two for the fractional part with chopping would be \(0.01\), that is, \(10^{- p}\) where \(p\) is the number of places used for the fractional part.
What would be the upper bound on the absolute true error be if, instead of chopping, rounding is used? It would be \(0.005\), that is, \(0.5 \times 10^{- p}\), where \(p\) is the number of places used for the fractional part.
Check this upper bound on the absolute true error out for yourself for a different configuration and different rounding-off choices. That is, choose a certain number of places for the integer and fractional parts, and use rounding or chopping.
A base-10 non-negative number is represented using the fixed format with 8 places, where 3 places are used for the integer part, and 5 places are used for the fractional part. Chopping is used.
a) What is the upper bound on the absolute true error in representing a number?
b) What is the smallest value that can be represented?
c) What is the largest number that can be represented?
Solution
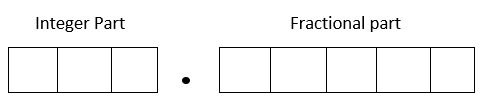
a) The fixed-point format for base-10 numbers is the same as the decimal format. In the example, 3 places are used for the integer part, and 5 places are used for the fractional part. Also, only non-negative numbers (greater than or equal to zero) are represented.
To find the upper bound on the absolute true error in representing a number, take any two consecutive numbers that can be represented exactly. For example,


There are infinite numbers between the two. The number (recall that the line over 9 as \(\bar{9}\) stands for 9 being a recurring number)
\[259.73284\bar{9} \nonumber\]
would create the largest true error as it would get represented as \[259.73284 \nonumber\]
because chopping is used to represent the numbers. The absolute true error is
\[\begin{split} |E_t| &= |259.73284\bar{9} - 259.73284|\\ &=|0.00000\bar{9}|\\ &= 0.00000\bar{9} \end{split} \nonumber\]
making
\[|E_t|<0.00001=10^{-5} \nonumber\]
You can try any other two consecutive numbers, and you would find that \(|E_t|<10^{-5}\). Did you recognize that \(5\) is the number of places used for the fractional part?
Can you repeat the problem when rounding is used?
b) The smallest number that can be represented would have zeros in all the places, that is, \(000.00000\) and that would be simply zero.

c) The largest that can be represented would have 9’s in all places, that is, \(999.99999\).

Floating-point representation
If I am interested in keeping relative true errors similar in magnitude for the range of numbers, what alternatives do I have?
To keep the relative true error in the representation of numbers to be of a similar order for all numbers, one uses the floating-point representation of the number. You may know it better as the scientific format, but that terminology is only used for base-\(10\) numbers, and that is the case here.
For example, in floating-point representation, a number
\[256.78 \text{ is written as } + 2.5678 \times 10^{2}, \nonumber\]
\[0.003678 \text{ is written as } + 3.678 \times 10^{- 3},\ \text{and} \nonumber\]
\[- 256.789 \text{ is written as } - 2.56789 \times 10^{2}. \nonumber\]
The general representation of a number in base-\(10\) format is given as
\[\text{sign}\ \times \ \text{mantissa}\ \times \ 10^{\text{sign of exponent } \times \text{ magnitude of exponent}} \nonumber\]
or for a number \(y\),
\[y = \sigma \times m \times 10^{ \ p \times e} \nonumber\]
where
\[\sigma = \text{sign of the number, } + { 1 \text{ or} -1}, \nonumber\]
\[m\ = \text{ mantissa, }1 \leq \ m < {10} \nonumber\]
\[p = \text{sign of the exponent, } + { 1 \ \text{or} -1} \nonumber\]
\[e\ = \text{integer exponent magnitude (also called ficand)} \nonumber\]
Let us go back to the example where we had five spaces available for representing a number as in the cash register. Let us limit ourselves to positive numbers as we did previously but now also to positive exponents. Using the same number of five spaces, let us use the first four spaces for the mantissa and the last one for the exponent. The smallest number that can be represented is \(1.000 \times 10^{0}\), and the largest number that can be represented is \(9.999 \times 10^{9}\). The smallest number is not zero as the floating-point representation requires us to put a non-zero number before the decimal point, and the smallest non-zero number is 1. By using the floating-point representation, what we lose in accuracy, we gain in the range of numbers that can be represented. For our example, the range of numbers represented in the five spaces is [\(0\),\(\ 999.99\)] for the fixed format and [\(1\), \(\ 9.999 \times 10^{9}\)] for the floating-point (scientific) format.
How would one represent a number in the floating-point format?
Take the previous example of \(256.78\). It would be represented as \(2.567 \times 10^{2}\) if chopping is used and \(2.568 \times 10^{2}\) if rounding is used.
Another example, the number \(576329.78\), would be represented as \(5.763 \times 10^{5}\) if chopping is used and \(5.763 \times 10^{5}\) if rounding is used.
So, how much error is caused by the floating-point format representation using chopping?
In representing, say \(256.78\), it would be represented as \(2.567\times10^2\). The round-off error created is
\[E_t=256.78 - 2.567 \times 10^{2} = 0.08, \nonumber\]
and the relative true error is
\[\varepsilon_{t} = \frac{0.08}{256.78} = 0.00031155, \nonumber\]
In representing another number, \(576329.78\), it would be represented as \(5.763\times10^5\). The round-off error created is
\[E_t=576329.78 - 5.763 \times 10^{5} = 29.78, \nonumber\]
and the relative true error is
\[\varepsilon_{t} = \frac{29.78}{576329.78} = 0.000051672. \nonumber\]
In representing, \(576399.99\), it would be represented as \(5.763\times10^5\). The round-off error created is
\[E_t=576399.99 - 5.763 \times 10^{5} = 99.99, \nonumber\]
and the relative true error is
\[\varepsilon_{t} = \frac{99.99}{576399.99} = 0.00017347. \nonumber\]
In representing, \(1.0009999\), it would be represented as \(1.000\times10^0\). The round-off error created is
\[E_t=1.0009999 - 1.000 \times 10^{0} = 0.0009999, \nonumber\]
and the relative true error is
\[\varepsilon_{t} = \frac{0.0009999}{1.0009999}= 0.00099890. \nonumber\]
What you see through these examples about the floating-point format is that although the true errors are large for large numbers and small for small numbers, it is the relative true errors that stay in the similar order for large as well as small numbers. In fact, the magnitude of the relative true error for any number that can be represented in the above configuration of four places for the mantissa and one for the exponent with chopping would be \(0.001\), that is, \(10^{1-p}\), where \(p\) is the number of places used for the mantissa.
What would the upper bound on the absolute relative true error be if, instead of chopping, rounding is used. It would be \(0.0005\), that is, \(0.5 \times 10^{1-p}\) , where \(p\) is the number of places used for the mantissa.
Check this upper bound on the absolute relative true error out for yourself for a different configuration and different rounding-off choices. That is, choose a certain number of places for the mantissa and exponential parts, and use rounding or chopping.
A base-10 non-negative number is represented using floating-point format with only non-negative exponents and 8 places, where 5 places are used for the mantissa and 2 places are used for the exponent part. Chopping is used.
a) What is the upper bound on the absolute relative true error in representing a number?
b) What is the smallest value that can be represented?
c) What is the largest number that can be represented?
Solution
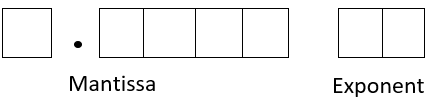
a) The floating point format for base-10 numbers is the same as the scientific format. 5 places are used for the mantissa and 2 places are used for the exponent. The numbers are non-negative (greater than or equal to zero) and the exponents are non-negative (greater than or equal to zero).
To find the upper bound on the absolute relative true error in representing a number, take two consecutive numbers


There are infinite numbers between the two. The number
\[1.0000\bar{9} \times 10^0 \nonumber\]
would create the largest true error as it would be represented as
\[1.0000 \times 10^0 \nonumber\]
as chopping is used.
The absolute true error is
\[\begin{split} |E_t| &= |1.0000\bar{9} \times 10^0 - 1.0000 \times 10^0|\\ &=0.0000\bar{9}\end{split} \nonumber\]
The absolute relative true error is
\[\begin{split} |\epsilon_t| &= \left| \frac{1.0000\bar{9} \times 10^0 - 1.0000 \times 10^0}{1.0000\bar{9} \times 10^0}\right|\\ &= 0.000099998\\ &<0.0001\\ &=10^{-4} \end{split} \nonumber\]
Any other number other than the one shown above would also yield an absolute relative true error which is less than \(10^{-4}\), and hence \(10^{-4}\) is an upper limit on the absolute relative true error in representing a number. Did you recognize that \(|\epsilon_t|<10^{-4}\) for all numbers where \(-4=1-5\), and \(5\) is the number of places used for the magnitude of the mantissa?
b) The smallest number that can be represented is

which is simply
\[\begin{split} &1.0000 \times 10^0 \\ &=1 \end{split} \nonumber\]
The scientific notation requires us to put a non-zero number before the decimal point, and the smallest non-zero number is 1.
c) The largest number that can be represented is

which is \[9.9999\times 10^{99} \nonumber\]
Can you repeat the problem when rounding is used?
Audiovisual Lecture
Title: Floating Point Representation of Numbers
Summary: This video shows that before delving into floating point representation in binary format, we would be better off by revisiting fixed (decimal) format and floating point (scientific) format for base-10 numbers. The limits on the range of numbers representable, true errors, and relative true errors is looked at. This will ease the student into the floating point representation of binary numbers.
Lesson 2: Introduction to Binary Floating-Point Representation of Numbers
Learning Objectives
After successful completion of this lesson, you should be able to:
1) convert a base-10 number to a binary floating-point representation
2) convert a binary floating-point number to its equivalent base-10 number
How does the floating-point format work for binary representation?
A number \({y }\) would be written as
\[y=\sigma\times m\times 2^{p\times e} \nonumber\]
where
\[\sigma = \text{sign of number (negative or positive),} \nonumber\]
\[m = \text{magnitude of mantissa, } \left( 1 \right)_{2} \leq m < \left( 10 \right)_{2} ,\ \text{that is, } \left( 1 \right)_{10} \leq m < \left( 2 \right)_{10}, \nonumber\]
\[p = \text{sign of the exponent (negative or positive)} \nonumber\]
\[e = \text{magnitude of the exponent (an integer).} \nonumber\]
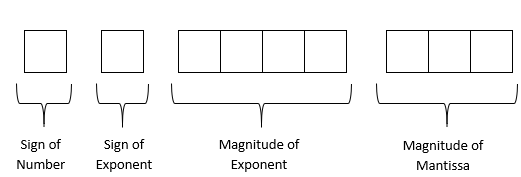
So, how will the number be stored in a binary floating-point format? Let us suppose a real number is represented in an \(8\)-bit format (this is hypothetical and is chosen to keep the explanation simple) in a computer, and the architecture used by it is as follows – first bit is used for the sign of the number, second bit for the sign of the exponent, next four bits for the magnitude of the mantissa and the last two bits for the exponent.
In the first bit, you will put a \(0\) in it if the number is positive and \(1\) if it is negative.
In the second bit, you will put a \(0\) if the exponent is positive and \(1\) if it is negative.
In the next four bits, you will put the magnitude of the mantissa less one. Why? Since the magnitude of the mantissa is always greater than or equal to one and strictly less than \(2\), the leading \(1\) is not stored in the four bits of the mantissa, and only the digits after the radix point are stored.
In the next two bits, you will put the magnitude of the exponent.
Looking at the example will make it clear how a number is represented in floating-point binary format.
Represent \(\left( 54.75 \right)_{10}\) in floating-point binary format. Assume that the number is written to a hypothetical format that is \(9\) bits long where the first bit is used for the sign of the number, the second bit for the sign of the exponent, the next four bits for the magnitude of the mantissa, and the next three bits for the magnitude of the exponent.
Solution
The format for the use of the 9-bits is as follows
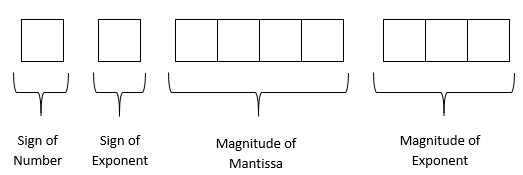
Following the procedure in Chapter 01.04, the fixed-point binary format of the given base-\(10\) number is
\[\left( 54.75 \right)_{10} = (110110.11)_{2} \nonumber\]
Writing the number in floating-point format, we get
\[\left( 54.75 \right)_{10} = \left( 1.1011011 \right)_{2} \times 2^{(5)_{10}} \nonumber\]
The exponent \(5\) is equivalent in binary format as
\[\left( 5 \right)_{10} = \left( 101 \right)_{2} \nonumber\]
Hence
\[\left( 54.75 \right)_{10} = \left( 1.1011011 \right)_{2} \times 2^{(101)_{2}} \nonumber\]
The sign of the number is positive, so the bit for the sign of the number will have zero in it.
The sign of the exponent is positive. So, the bit for the sign of the exponent will have zero in it.
The magnitude of mantissa will be
\[m = 1011 \nonumber\]
(There are only \(4\) places for the mantissa, and the leading \(1\) is not stored as it is always 1 by default).
The magnitude of the exponent is
\[e = 101 \nonumber\]
We now have the representation as

What number does the below given floating point format represent in base-\(10\) format?

Assume a hypothetical 9-bit word, where the first bit is used for the sign of the number, the second bit for the sign of the exponent, the next four bits for the magnitude of mantissa and the next three for the magnitude of the exponent.
Solution
The format for the use of the 9-bits is as follows

Given
| Bit Representation | Part of Floating-point number |
|---|---|
| \(0\) | Sign of number |
| \(1\) | Sign of exponent |
| \(1011\) | Magnitude of mantissa |
| \(110\) | Magnitude of exponent |
The first bit is \(0\), so the number is positive.
The second bit is \(1\), so the exponent is negative.
The next four bits, \(1011\), represent the magnitude of the mantissa.
The next three bits, \(110\), represent the magnitude of the exponent.
The number in binary format hence is
\[\displaystyle \left( 1.1011 \right)_{2} \times 2^{- \left( 110 \right)_{2}} \nonumber\]
The magnitude of the mantissa is
\[\begin{split} m &= \left( 1.1011 \right)_{2}\\ &= \left( 1 \times 2^{0} + 1 \times 2^{- 1} + 0 \times 2^{- 2} + 1 \times 2^{- 3} + 1 \times 2^{- 4} \right)_{10}\\ &= \left( 1.6875 \right)_{10}\end{split} \nonumber\]
The magnitude of the exponent is
\[\begin{split} e &= \left( 110 \right)_{2}\\ &= \left( 1 \times 2^{2} + 1 \times 2^{1} + 0 \times 2^{0} \right)_{10}\\ &= \left( 6 \right)_{10}\end{split} \nonumber\]
Hence, the number \(\left( 1.1011 \right)_{2} \times 2^{- \left( 110 \right)_{2}}\) in base-10 format is
\[\begin{split} &= \left( 1.6875 \times 2^{- 6} \right)_{10}\\ &=(0.026367)_{10}\end{split} \nonumber\]
A machine stores floating-point numbers in a hypothetical \(10\)-bit binary word. It employs the first bit for the sign of the number, the second one for the sign of the exponent, the next four bits for the magnitude of the exponent, and the last four for the magnitude of the mantissa.
a) Find how \(0.02832\) will be represented in the floating-point 10-bit word.
b) What is the decimal equivalent of the 10-bit word representation of part (a)?
Solution
The format for the use of the 10-bits is as follows
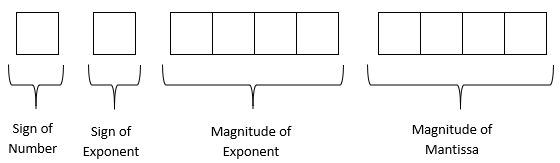
a) For the number, we have the integer part as \(0\), and the fractional part as \(0.02832.\)
Let us first find the binary equivalent of the integer part
Integer part \[\left( 0 \right)_{10} = \left( 0 \right)_{2} \nonumber\]
Now we find the binary equivalent of the fractional part
| Number | Number after decimal | Number before decimal | |
|---|---|---|---|
| \(0.02832 \times 2\) | \(0.05664\) | \(0.05664\) | \(0 = a_{-1}\) |
| \(0.05664 \times 2\) | \(0.11328\) | \(0.11328\) | \(0=a_{-2}\) |
| \(0.11328\times 2\) | \(0.22656\) | \(0.22656\) | \(0=a_{-3}\) |
| \(0.22656\times 2\) | \(0.45312\) | \(0.45312\) | \(0=a_{-4}\) |
| \(0.45312\times 2\) | \(0.90624\) | \(0.90624\) | \(0=a_{-5}\) |
| \(0.90624 \times 2\) | \(1.81248\) | \(0.81248\) | \(1=a_{-6}\) |
| \(0.81248 \times 2\) | \(1.62496\) | \(0.62496\) | \(1=a_{-7}\) |
| \(0.62496 \times 2\) | \(1.24992\) | \(0.24992\) | \(1=a_{-8}\) |
| \(0.24992\times 2\) | \(0.49984\) | \(0.49984\) | \(0=a_{-9}\) |
| \(0.49984\times 2\) | \(0.99968\) | \(0.99968\) | \(0=a_{-10}\) |
| \(0.99968\times 2\) | \(1.99936\) | \(0.99936\) | \(1=a_{-11}\) |
Hence
\[\begin{split} \left( 0.02832 \right)_{10} &\cong \left( 0.00000111001 \right)_{2}\\ &= \left( 1.11001 \right)_{2} \times 2^{- 6}\\ &\cong \left( 1.1100 \right)_{2} \times 2^{- 6} \end{split} \nonumber\]
The binary equivalent of the magnitude of the exponent \(6\) is found as follows
| Quotient | Remainder | |
|---|---|---|
| \(6/2\) | \(3\) | \(0 = a_{0}\) |
| \(3/2\) | \(1\) | \(1 = a_{1}\) |
| \(1/2\) | \(0\) | \(1 = a_{2}\) |
So
\[\left( 6 \right)_{10} = \left( 110 \right)_{2} \nonumber\]
Hence
\[\begin{split} \left( 0.02832 \right)_{10} &= \left( 1.1100 \right)_{2} \times 2^{- \left( 110 \right)_{2}}\\ &= \left( 1.1100 \right)_{2} \times 2^{- \left( 0110 \right)_{2}}\end{split} \nonumber\]
| Part of Floating-point number | Bit Representation |
|---|---|
| Sign of number is positive | \(0\) |
| Sign of exponent is negative | \(1\) |
| Magnitude of the exponent | \(0110\) |
| Magnitude of mantissa | \(1100\) |
The ten-bit representation bit by bit is

b) Converting the above floating-point representation from part (a) to base \(10\) by following Example \(\PageIndex{2.2}\) gives
\[\begin{split} &\left( 1.1100 \right)_{2} \times 2^{- \left( 0110 \right)_{2}}\\ &= \left( 1 \times 2^{0} + 1 \times 2^{- 1} + 1 \times 2^{- 2} + 0 \times 2^{- 3} + 0 \times 2^{- 4} \right) \times 2^{- \left( 0 \times 2^{3} + 1 \times 2^{2} + 1 \times 2^{1} + 0 \times 2^{0} \right)}\\ &= \left( 1.75 \right)_{10} \times 2^{- \left( 6 \right)_{10}}\\ &= 0.02734375\end{split} \nonumber\] which is different from the original number which was \(0.02832\).
A machine stores a floating-point number in a hypothetical 9-bit word. It uses the first bit for the sign of the number, the second bit for the sign of the exponent, the next four bits for the magnitude of the exponent, and the last 3 bits for the magnitude of the mantissa.
a) What is the smallest base-10 positive number that can be represented in the given format?
b) What is the largest base-10 positive number that can be represented in the given format?
Solution
a) The format for the use of the 9-bits is as follows:
Since we are looking for the smallest positive number, the first bit for the sign of the number would be 0 as the number is positive. The second bit for the sign of the exponent would be 1 as that would give a negative exponent of 2, and hence result in a smaller number.
The next four bits would be filled with 1’s because that will give us the largest exponent by the magnitude, and with the second bit being 1, it would make the exponent negative.
The next three bits of the magnitude of mantissa would be filled with 0’s for the smallest number.
So the 9 bits would be

giving us
\[\begin{split} &+ (1.000)_2 \times 2^{-(1111)_2} \\ &= (1\times 2^0) \times 2^{-(1\times2^3 + 1\times2^2 + 1\times2^1 + 1\times2^0)} \\ &= 1 \times 2^{-(8+4+2+1)} \\ &= 2^{-15} \\ & = 0.0000305176 \end{split} \nonumber\]
b) The format is as follows

Since we are looking for the largest positive number, the first bit for the sign of the number would be 0 as the number is positive. The second bit for the sign of the exponent would be 0 as that would give a positive exponent of 2, and result in a larger number.
The next four bits would be filled with 1’s because that will give us the largest exponent by the magnitude, and with the second bit being 0, it would be a positive exponent.
The next three bits for the magnitude of the mantissa would be filled with 1’s for the largest number.
So the 9 bits would be

giving us
\[\begin{split} &+ (1.111)_2 \times 2^{+(1111)_2} \\ &= (1\times 2^0 + 1\times 2^{-1} + 1\times 2^{-2} + 1\times 2^{-3}) \times 2^{(1\times2^3 + 1\times2^2 + 1\times2^1 + 1\times2^0)} \\ &= 1.875 \times 2^{(15)} \\ & = 28672.0 \end{split} \nonumber\]
Audiovisual Lectures
Title: Floating Point Representation - Example
Summary: In a previous lesson, we learned how to convert a base-10 number to a base-2 fixed point format. In this example, we convert it to a base-2 floating point format.
Lesson 3: Binary Floating-Point Representation of Numbers with Biased Exponent
Learning Objectives
After successful completion of this lesson, you should be able to:
1) convert a base-10 number to a binary floating-point representation with a biased exponent
2) convert a binary floating-point number with a biased exponent to its equivalent base-10 number
What is the floating-point format with a biased exponent for binary format? How is it different from the floating-point format with an unbiased exponent?
A number \(y\) would be written as
\[\displaystyle y = \sigma \times m \times 2^{e} \nonumber\]
where
\[\sigma = \text{sign of the number (negative or positive - use 0 for positive and 1 for negative),} \nonumber\]
\[m = \text{magnitude of mantissa, } \left( 1 \right)_{2} \leq m < \left( 10 \right)_{2} ,\text{ that is, } \left( 1 \right)_{10} \leq m < \left( 2 \right)_{10},\text{ and} \nonumber\]
\[e = \text{integer } biased \text{ exponent.} \nonumber\]
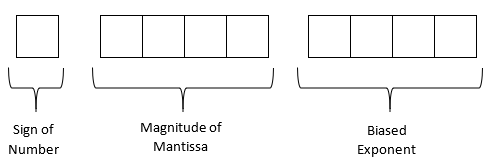
The only difference between the previous lesson of the binary floating-point format is that the exponent was unbiased in the previous lesson. In the unbiased exponent format, one bit was used for the sign of the exponent, and several bits were used for the magnitude of the exponent. In the biased exponent format, no bit is used for the sign of the exponent, and that bit is added to be used for the magnitude of the biased exponent. The reasons for using biased exponent are varied, but it is sufficient to say that it reduces computational effort and increases the range of representable numbers.
Let us suppose we are using \(3\) bits for the magnitude of the unbiased exponent and \(1\) bit for the sign of the exponent. For the unbiased exponent, we would then use \(4\) bits. But if there is no bit used for the sign of the number, how would we represent negative exponents. The following is how it is done.
The biased exponent is equally divided between negative and positive exponents. For example, we have four bits now for the biased exponent, and hence the minimum base-\(10\) possible number that can be represented is
\[{(0000)}_{2}={(0)}_{10} \nonumber\]
and the maximum base-\(10\) possible number is
\[(1111)_{2}=(15)_{10}. \nonumber\]
Half of the maximum value is \(7.5\), and the integer part of it is \(7\). Hence, we will bias the unbiased exponent by \(7\) (add \(7\)) and then store that value. When we have to unpack the exponent to its actual value, we will unbias it by \(7\) (subtract \(7\)) from it. For example, if the following binary number
\[y = {(1.011)}_{2} \times 2^{- {(110)}_{2}} \nonumber\]
is represented with 4 bits for the biased exponent, we would proceed as follows. The exponent \(- {(110)}_{2}\) is equivalent to \(- {(6)}_{10}\). So, the biased exponent becomes
\[- 6 + 7 = 1. \nonumber\]
Then
\[{(1)}_{10} = {(0001)}_{2}. \nonumber\]
Hence we would store the biased exponent in binary as \(0001\). If we had to unpack it, the biased exponent would be
\[{(0001)}_{2} = {(1)}_{10} \nonumber\]
and the unbiased exponent in base-\(10\) would be
\[1 - 7 = - 6. \nonumber\]
Represent \(\left( 54.75 \right)_{10}\) in floating point binary format. Assume that the number is written to a hypothetical word that is \(9\) bits long where the first bit is used for the sign of the number, the next four bits for the magnitude of the mantissa, and the next four bits for the magnitude of the biased exponent.
Solution
The format for the use of 9 bits is as follows
Following procedures in Chapter 01.04, we get the fixed-point binary equivalent as
\[\left( 54.75 \right)_{10} = (110110.11)_{2} \nonumber\]
Writing the number in floating-point format, we get
\[\left( 54.75 \right)_{10} = \left( 1.1011011 \right)_{2} \times 2^{(5)_{10}} \nonumber\]
Since the number of bits used for the biased exponent is \(4\), the bias would be by integer part of half of (\(1111)_{2}\) to give \(int(15/2) = \left( 7 \right)_{10}\). The biased exponent hence in base-10 is \(5 + 7 = 12\)
The biased exponent \(12\) is equivalent in binary format as
\[\left( 12 \right)_{10} = \left( 1100 \right)_{2} \nonumber\]
Hence
\[\left( 54.75 \right)_{10} = \left( 1.1011011 \right)_{2} \times 2^{(1100)_{2}} \text{ (with biased exponent)} \nonumber\]
The sign of the number is positive, so the bit for the sign of the number will have zero in it.
\[\sigma = 0 \nonumber\]
There are only \(4\) places for the mantissa, and the leading \(1\) is not stored as it is always expected to be there. The magnitude of mantissa will be represented as
\[m = 1011 \nonumber\]
(There are only \(4\) places for the mantissa, and the leading \(1\) is not stored as it is always 1 by default).
The magnitude of the biased exponent is
\[e = 1100, \nonumber\]
and we have the representation as

What number does the below-given floating-point format with a biased exponent represent in base-\(10\) format?

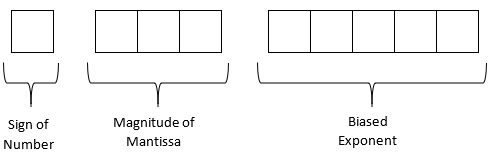
Assume a hypothetical \(9\)-bit word, where the first bit is used for the sign of the number, the next three bits for the magnitude of mantissa, and the next five for the magnitude of the biased exponent.
Solution
The format for the use of 9 bits is as follows.
Given
| Bit Representation | Part of Floating point number |
|---|---|
| \(1\) | The sign of the number |
| \(110\) | The magnitude of the mantissa |
| \(11010\) | The magnitude of the biased exponent |
The first bit is \(1\), so the number is negative.
The next three bits, \(110\), are the magnitude of the mantissa.
The next five bits, \(11010\), are for the biased exponent
Because there are five bits for the biased exponent, the bias would be by integer part of half of \((11111)_{2}\) to give
\[int(31/2) = \left( 15 \right)_{10}. \nonumber\]
The biased exponent is
\[\left( 11010 \right)_{2} = \left( 26 \right)_{10}, \nonumber\]
and hence the unbiased (actual) exponent is
\[26-15=11 \text{ in base-10.} \nonumber\]
Now
\[\left( 11 \right)_{10} = \left( 1011 \right)_{2} \nonumber\]
The number in binary format hence is
\[{- \left( 1.110 \right)}_{2} \times 2^{\left( 1011 \right)_{2}} \nonumber\]
The magnitude of the mantissa is
\[\begin{split} m &= \left( 1.110 \right)_{2}\\ &= (1 \times 2^0 + 1 \times 2^{-1}+1 \times 2^{-2}+0 \times 2^{-3})_{10}\\ &= (1.75)_{10} \end{split} \nonumber\]
The magnitude of the exponent is
\[\begin{split} e &= \left( 1011 \right)_{2}\\ &= 11\end{split} \nonumber\]
The number in the base-\(10\) format hence is
\[\begin{split} &= - 1.75 \times 2^{11}\\ &= - 3584\end{split} \nonumber\]
Appendix
How are numbers represented in floating-point in a real computer?
In an actual typical computer, a real number is stored as per the IEEE-754 (Institute of Electrical and Electronics Engineers) floating-point arithmetic format. To keep the discussion short and simple, let us point out the salient features of the single-precision format.
- A single-precision number uses \(32\) bits.
- A number \(y\) is represented as (note the \(1\) before the radix point):
\[y = \sigma \times \left( 1.a_{1}a_{2}\ldots a_{23} \right) \cdot 2^{e} \nonumber\]
where
\[\sigma = \text{sign of the number (positive or negative)} \nonumber\]
\[a_{i} = \text{entries of the mantissa can be only } 0 \text{ or } 1 \text{ for } i = 1,...,23 \nonumber\]
\[e = \text{the exponent} \nonumber\]
- The first bit represents the sign of the number (\(0\) for a positive number and \(1\) for a negative number).
- The next eight bits represent the biased exponent. Note that there is no separate bit for the sign of the exponent. The sign of the exponent is taken care of by normalizing by adding \(127\) to the actual exponent. For example, in the previous example, the exponent was \(6\). It would be stored as the binary equivalent of \(127 + 6 = 133\). Why is \(127\) and not some other number added to the actual exponent? Because in eight bits, the largest integer that can be represented is \(\left( 11111111 \right)_{2} = 255\), and halfway of \(255\) is \(127\) (integer part of \(255/2\)). This allows negative and positive exponents to be represented equally. The normalized (also called biased) exponent has the range from \(0\) to \(255\), and hence the exponent \(\text{e }\)has the range of \(- 127 \leq e \leq 128\).
- If instead of using the biased exponent, let us suppose we still used eight bits for the exponent but used one bit for the sign of the exponent and seven bits for the exponent magnitude. In seven bits, the largest integer that can be represented is \(\left( 1111111 \right)_{2} = 127,\) in which case the exponent \(e\) range would have been smaller, that is,\(- 127 \leq e \leq 127\). By biasing the exponent, the unnecessary representation of a negative zero and positive zero exponents (which are the same) is also avoided.
- Actually, the biased exponent range used in the IEEE-754 format is not \(0\) to \(255\), but \(1\) to \(254\). Hence, exponent \(e\) has a range of \(- 126 \leq e \leq 127\). So what are \(e = - 127\) and \(e = 128\) used for? If \(e = 128\) and all the mantissa entries are zeros, the number is \(\pm \infty\) (the sign of infinity is governed by the sign bit), if \(e = 128\) and the mantissa entries are not zero, the number being represented is Not a Number (NaN). Because of the leading \(1\) in the floating-point representation, the number zero cannot be represented exactly. That is why the number zero (\(0\)) is represented by \(e = - 127\) and all the mantissa entries being zero.
- The next twenty-three bits are used for the magnitude of the mantissa.
- The largest number by magnitude that is represented by this format is
\[\left( 1 \times 2^{0} + 1 \times 2^{- 1} + 1 \times 2^{- 2} + \ldots + 1 \times 2^{- 22} + 1 \times 2^{- 23} \right) \times 2^{127} = 3.40 \times 10^{38} \nonumber\]
The smallest number by magnitude that is represented, other than zero, is
\[\left( 1 \times 2^{0} + 0 \times 2^{- 1} + 0 \times 2^{- 2} + \ldots + 0 \times 2^{- 22} + 0 \times 2^{- 23} \right) \times 2^{- 126} = 1.18 \times 10^{- 38} \nonumber\]
Since 23 bits are used for the mantissa, the machine epsilon is
\[\begin{split} \epsilon_{mach} &= 2^{- 23}\\ &= 1.19 \times 10^{- 7}. \end{split} \nonumber\]
How are numbers represented in floating-point in double precision in a computer?
In double-precision of IEEE-754 format, a real number is stored in \(64\) bits.
- The first bit is used for the sign,
- the next \(11\) bits are used for the exponent, and
- the rest of the bits that are \(52\) are used for the mantissa.
So here are some questions that you may want to ask yourself. For double-precision format, can you find the following?
- the range of the biased exponent,
- the range of the corresponding unbiased exponent
- the smallest number that can be represented,
- the largest number that can be represented, and
- machine epsilon
Lesson 4: Accuracy of Binary Floating-Point Representation of Numbers
Learning Objectives
After successful completion of this lesson, you should be able to:
1) define machine epsilon
2) relate the round-off error in representing numbers to machine epsilon
How do you determine the accuracy of a floating-point binary format number?
The machine epsilon, \(\epsilon_{mach}\) is a measure of the accuracy of a floating-point representation and is found by calculating the difference between \(1\) and the next number that can be represented as a machine number. That is machine epsilon, \(\epsilon_{mach}\) is defined as the smallest number such that
\[ 1+\epsilon_{mach}> 1 \nonumber\]
For example, assume a \(10\)-bit hypothetical computer where the first bit is used for the sign of the number, the second bit for the sign of the exponent, the next four bits for the magnitude of the exponent and the next four for the magnitude of the mantissa.
We represent \(\left( 1 \right)_{10}\) as \(\left( 1.0000 \right)_{2} \times 2^{(0000)_{2}}\) and hence in the \(10\)-bits is represented as

The next higher number would be \(\left( 1.0001 \right)_{2} \times 2^{(0000)_{2}}\)and that will be represented in the \(10\)-bits as

The difference between the two numbers is
\[\begin{split} &\left( 1.0001 \right)_{2} \times 2^{(0000)_{2}} - \left( 1.0000 \right)_{2} \times 2^{(0000)_{2}}\\ &=\left( 0.0001 \right)_{2} \times 2^{(0000)_{2}}\\ &= (0 \times 2^{- 1} + 0 \times 2^{- 2} + 0 \times 2^{- 3} + 1 \times 2^{- 4})_{10} \times 2^{(0)_{10}}\\ &= (0.0625)_{10} \times (1)_{10}\\ &= (0.0625)_{10}.\end{split} \nonumber\]
The machine epsilon is
\[\epsilon_{mach} = 0.0625. \nonumber\]
The machine epsilon, \(\epsilon_{mach}\), can also simply be calculated as two to the negative power of the number of bits used for the mantissa.
\[\begin{split} \epsilon_{mach}\ &=\ 2^{-{bits\ used\ for\ magnitude\ of\ mantissa}}\\ &= 2^{- 4}\\ &= 0.0625\end{split} \nonumber\]
What is the significance of machine epsilon for a student in an introductory course in numerical methods?
The machine epsilon is an upper bound on the absolute relative true error in representing a number. Let \(y\) be the machine number representation of a number\(\ x;\) then we can show that the absolute relative true error in the representation is
\[\left| \frac{x - y}{x} \right| \leq \epsilon_{mach} \nonumber\]
An example to illustrate follows.
A machine stores floating-point numbers in a hypothetical \(10\)-bit binary word. It employs the first bit for the sign of the number, the second one for the sign of the exponent, the next four bits for the magnitude of the exponent, and the last four bits for the magnitude of the mantissa. Confirm that the magnitude of the relative true error that results from the approximate representation of \(0.02832\) in the \(10\)-bit format is less than the machine epsilon.
Solution
From an example in an earlier lesson, the ten-bit representation of \(0.02832\) bit-by-bit for the above architecture is

Again from the same example, converting the above floating-point representation to base-10 gives
\[\begin{split} &\left( 1.1100 \right)_{2} \times 2^{- \left( 0110 \right)_{2}}\\ &= \left( 1.75 \right)_{10} \times 2^{- \left( 6 \right)_{10}}\\ &= \left( 0.02734375 \right)_{10}\end{split} \nonumber\]
The absolute relative true error between the base-10 numbers 0.02832 and its approximate representation 0.02734375 is
\[\begin{split} \left| \varepsilon_{t} \right| &= \left| \frac{0.02832 - 0.02734375}{0.02832} \right|\\ &= 0.034472 \end{split} \nonumber\]
which is less than the machine epsilon for a computer that uses 4 bits for the magnitude of mantissa, that is,
\[\begin{split} \varepsilon_{mach} &= 2^{- 4}\\ &= 0.0625\end{split} \nonumber\]
Take any other number that can be represented in the above format, and you will find that the absolute relative true error will always follow this bound, \(0 \leq \left| \varepsilon_{t} \right| < \varepsilon_{mach}\) .
Appendix
What is the proof that the absolute relative true error in representing a number on a machine is always less than the machine epsilon?
That is, prove that if \(y\) is the machine number representation of a number \(x\), then show that the absolute relative true error in the representation is
\[\displaystyle \left| \frac{x - y}{x} \right| \leq \varepsilon_{mach} \nonumber\]
Proof:
Let’s limit the proof here to positive numbers and the use of chopping for machine representation.
If \(x\) is a positive number we want to represent, it will be between a machine number \(x_{b}\) below \(x\) and a machine number \(x_{u}\) above \(x\).
If
\[x_{b} = \left( 1.b_{1}b_{2} \ldots b_{m} \right)_{2} \times 2^{k} \nonumber\]
where
\[m = \text{number of bits used for the magnitude of the mantissa, then} \nonumber\]
\[\begin{split} x_{u} &= \left\lbrack (1.b_{1}b_{2}\ldots b_{m})_{2} + (0.00 \ldots 1)_{2} \right\rbrack \times 2^{k}\\ &= \left\lbrack (1.b_{1}b_{2} \ldots b_{m})_{2} + 2^{- m} \right\rbrack \times 2^{k}\\ &= (1.b_{1}b_{2} \ldots b_{m})_{2} \times 2^{k} + 2^{- m} \times 2^{k}\\ &= (1.b_{1}b_{2} \ldots b_{m})_{2} \times 2^{k} + 2^{- m + k} \end{split} \nonumber\]
Since \(x\) is getting represented either as \(x_{b}\) or \(x_{u}\),
\[\begin{split} \left| x - y \right| &\leq \left| x_{b} - x_{u} \right|\\ &= 2^{- m + k}\end{split} \nonumber\]
\[\begin{split} \left| \frac{x - y}{x} \right| &\leq \frac{2^{- m + k}}{x}\\ &\leq \frac{2^{- m + k}}{x_{b}}\\ &= \frac{2^{- m + k}}{(1 \cdot b_{1}b_{2} \ldots b_{m})_{2}2^{k}}\\ &= \frac{2^{- m}}{(1 \cdot b_{1}b_{2} \ldots b_{m})_{2}}\\ &\leq 2^{- m} = \varepsilon_{mach}\end{split} \nonumber\]
The above proof is for positive numbers that use chopping for machine representation. We can prove the same for negative numbers or when rounding is used for machine representation.
Multiple Choice Test
(1). A hypothetical computer stores real numbers in binary floating-point format in \(8\)-bit words. The first bit is used for the sign of the number, the second bit for the sign of the exponent, the next two bits for the magnitude of the exponent, and the next four bits for the magnitude of the mantissa. Represent \(e \approx 2.718\) in the \(8\)-bit format.
(A) \(00010101\)
(B) \(00011010\)
(C) \(00010011\)
(D) \(00101010\)
(2). A hypothetical computer stores real numbers in binary floating-point format in \(8\)-bit words. The first bit is used for the sign of the number, the second bit for the sign of the exponent, the next two bits for the magnitude of the exponent, and the next four bits for the magnitude of the mantissa. What is the base-\(10\) number represented by \((10100111)_{2}\)?
(A) \(-5.75\)
(B) \(-2.875\)
(C) \(-1.75\)
(D) \(-0.359375\)
(3). A hypothetical computer stores floating-point numbers in \(8\)-bit binary words. The first bit is used for the sign of the number, the second bit for the sign of the exponent, the next two bits for the magnitude of the exponent, and the next four bits for the magnitude of the mantissa. The machine epsilon is most nearly
(A) \(2^{- 8}\)
(B) \(2^{- 4}\)
(C) \(2^{- 3}\)
(D) \(2^{- 2}\)
(4). A machine stores floating-point numbers in \(7\)-bit binary word. The first bit is used for the sign of the number, the next three for the biased exponent, and the next three for the magnitude of the mantissa. The number \((0010110)_{2}\) represented in base-\(10\) is
(A) \(0.375\)
(B) \(0.875\)
(C) \(1.5\)
(D) \(3.5\)
(5). A machine stores floating-point numbers in \(7\)-bit binary word. The first bit is stored for the sign of the number, the next three for the biased exponent, and the next three for the magnitude of the mantissa. You are asked to represent \(33.35\) in the above word. The error you will get in this case would be
(A) underflow
(B) overflow
(C) NaN
(D) No error will be registered
(6). A hypothetical computer stores floating-point numbers in \(9\)-bit binary words. The first bit is used for the sign of the number, the second bit for the sign of the exponent, the next three bits for the magnitude of the exponent, and the next four bits for the magnitude of the mantissa. Every second, the error between \(0.1\) and its binary representation in the \(9\)-bit word is accumulated. The accumulated error in after one day most nearly is
(A) \(0.002344\)
(B) \(20.25\)
(C) \(202.5\)
(D) \(8640\)
For complete solution, go to
http://nm.mathforcollege.com/mcquizzes/01aae/quiz_01aae_floatingpoint_answers.pdf
Problem Set
(1). A hypothetical computer stores real numbers in floating-point format in \(8\)-bit binary words. The first bit is used for the sign of the number, the second bit for the sign of the exponent, the next two bits for the magnitude of the exponent, and the next four bits for the magnitude of the mantissa. Represent \(3.1415\) in the \(8\)-bit format.
- Answer
-
\(0\ 0\ 0\ 1\ 1\ 0\ 0\ 1\)
(2). A hypothetical computer stores real numbers in floating-point format in \(8\)-bit binary words. The first bit is used for the sign of the number, the second bit for the sign of the exponent, the next two bits for the magnitude of the exponent, and the next four bits for the magnitude of the mantissa. What number does \(10101111\) represent in the above given \(8\)-bit format?
- Answer
-
\(-7.75\)
(3). A hypothetical computer stores real numbers in floating-point format in \(10\)-bit binary words. The first bit is used for the sign of the number, the second bit for the sign of the exponent, the next three bits for the magnitude of the exponent, and the next five bits for the magnitude of the mantissa. Represent \(-0.0456\) in the \(10\)-bit format.
- Answer
-
\(1\ 1\ 1\ 0\ 1\ 0\ 1\ 1\ 1\ 0\)
(4). A hypothetical computer stores real numbers in floating-point format in \(10\)-bit binary words. The first bit is used for the sign of the number, the second bit for the sign of the exponent, the next three bits for the magnitude of the exponent, and the next five bits for the magnitude of the mantissa. What number does \(1011010011\) represent in the above given \(10\)-bit format?
- Answer
-
\(-102\)
(5). A machine stores floating-point numbers in \(7\)-bit binary words. Employ first bit for the sign of the number, second bit for the sign of the exponent, next two bits for the magnitude of the exponent, and the last three bits for the magnitude of the mantissa.
a) By magnitude, what are the smallest negative and positive numbers in the system?
b) By magnitude, what are the largest negative and positive numbers in the system?
c) What is the machine epsilon?
d) Represent \(e^{1}\) in the \(7\)-bit format.
e) Represent \(3.623\) in the \(7\)-bit format.
f) What is the next higher number, \(x_{2}\) after \(x_{1}\)= \(0 1 1 0 1 1 0\) in the 7-bit format.
g) Find \(\displaystyle \left| \frac{x_{2} - x_{1}}{x_{1}} \right|\) from part (f) and compare with the machine epsilon.
- Answer
-
\(a)\ -0.125,\ 0.125\ \ b)\ -15,\ 15\ \ c)\ 0.125\ \ d)\ 0\ 0\ 0\ 1\ 0\ 1\ 0\ \ e)\ 0\ 0\ 0\ 1\ 1\ 1\ 0\ \ f)\ 0.46875\)
\(g)\ 0.07142.\) This value is less than the machine epsilon of \(0.125.\) The absolute relative difference between consecutive numbers is always going to be less than the machine epsilon.

