Practice Makes Perfect
Recognize the Relation Between the Graph and the Slope–Intercept Form of an Equation of a Line
In the following exercises, use the graph to find the slope and \(y\)-intercept of each line. Compare the values to the equation \(y=mx+b\).
Exercise \(\PageIndex{1}\)
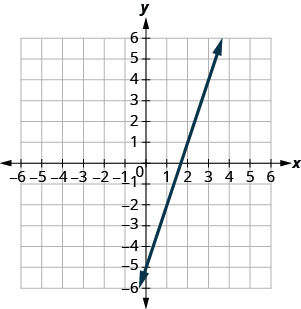
\(y=3x−5\)
Exercise \(\PageIndex{2}\)
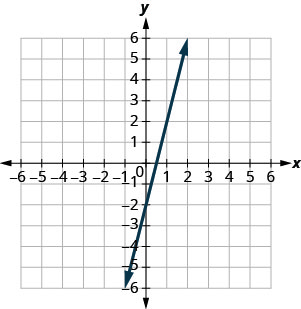
\(y=4x−2\)
- Answer
-
slope \(m=4\) and \(y\)-intercept \((0,−2)\)
Exercise \(\PageIndex{3}\)
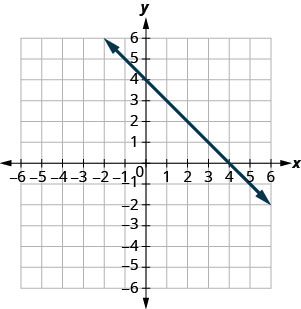
\(y=−x+4\)
Exercise \(\PageIndex{4}\)
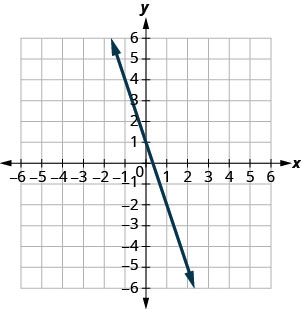
\(y=−3x+1\)
- Answer
-
slope \(m=−3\) and \(y\)-intercept \((0,1)\)
Exercise \(\PageIndex{5}\)
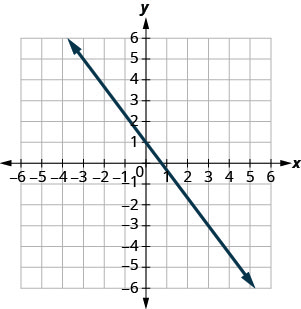
\(y=-\frac{4}{3} x+1\)
Exercise \(\PageIndex{6}\)
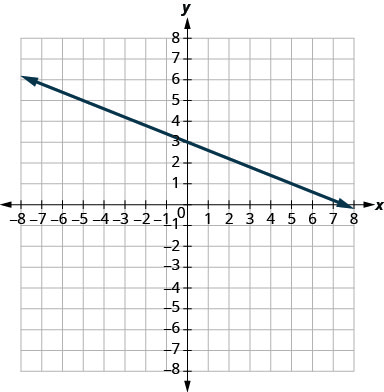
\(y=-\frac{2}{5} x+3\)
- Answer
-
slope \(m=-\frac{2}{5}\) and \(y\) -intercept \((0,3)\)
Identify the Slope and \(y\)-Intercept From an Equation of a Line
In the following exercises, identify the slope and \(y\)-intercept of each line.
Exercise \(\PageIndex{7}\)
\(y=−7x+3\)
Exercise \(\PageIndex{8}\)
\(y=−9x+7\)
- Answer
-
\(m = −9\); \(y\)-intercept: \((0,7)\)
Exercise \(\PageIndex{9}\)
\(y=6x−8\)
Exercise \(\PageIndex{10}\)
\(y=4x−10\)
- Answer
-
\(m = 4\); \(y\)-intercept: \((0,−10)\)
Exercise \(\PageIndex{11}\)
\(3x+y=5\)
Exercise \(\PageIndex{12}\)
\(4x+y=8\)
- Answer
-
\(m = −4\0; \(y\)-intercept: \((0,8)\)
Exercise \(\PageIndex{13}\)
\(6x+4y=12\)
Exercise \(\PageIndex{14}\)
\(8x+3y=12\)
- Answer
-
\(m = -\frac{8}{3}\); \(y\)-intercept: \((0,4)\)
Exercise \(\PageIndex{15}\)
\(5x−2y=6\)
Exercise \(\PageIndex{16}\)
\(7x−3y=9\)
- Answer
-
\(m = \frac{7}{3}\); \(y\)-intercept: \((0,-3)\)
Graph a Line Using Its Slope and Intercept
In the following exercises, graph the line of each equation using its slope and \(y\)-intercept.
Exercise \(\PageIndex{17}\)
\(y=x+3\)
Exercise \(\PageIndex{18}\)
\(y=x+4\)
- Answer
-
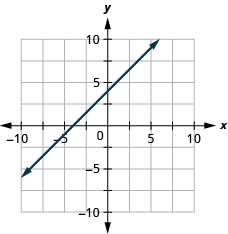
Exercise \(\PageIndex{19}\)
\(y=3x−1\)
Exercise \(\PageIndex{20}\)
\(y=2x−3\)
- Answer
-
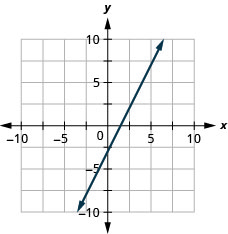
Exercise \(\PageIndex{21}\)
\(y=−x+2\)
Exercise \(\PageIndex{22}\)
\(y=−x+3\)
- Answer
-
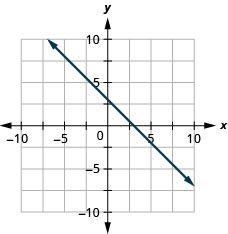
Exercise \(\PageIndex{23}\)
\(y=−x−4\)
Exercise \(\PageIndex{24}\)
\(y=−x−2\)
- Answer
-
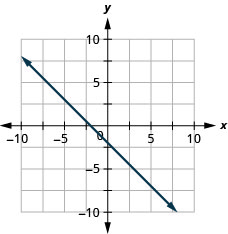
Exercise \(\PageIndex{25}\)
\(y=-\frac{3}{4}x-1\)
Exercise \(\PageIndex{26}\)
\(y=-\frac{2}{5}x-3\)
- Answer
-
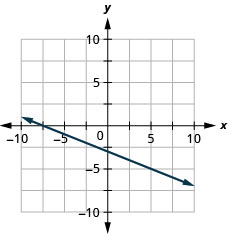
Exercise \(\PageIndex{27}\)
\(y=-\frac{3}{5}x+2\)
Exercise \(\PageIndex{28}\)
\(y=-\frac{2}{3}x+1\)
- Answer
-
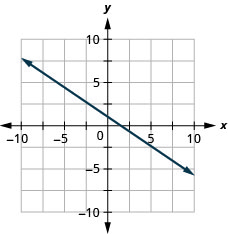
Exercise \(\PageIndex{29}\)
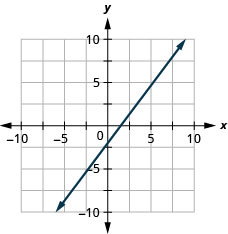
\(3x−4y=8\)
Exercise \(\PageIndex{30}\)
\(4x−3y=6\)
- Answer
-
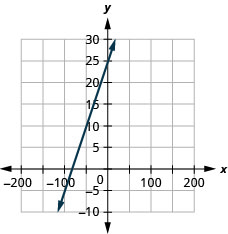
Exercise \(\PageIndex{31}\)
\(y=0.1x+15\)
Exercise \(\PageIndex{32}\)
\(y=0.3x+25\)
- Answer
-
Choose the Most Convenient Method to Graph a Line
In the following exercises, determine the most convenient method to graph each line.
Exercise \(\PageIndex{33}\)
\(x=2\)
Exercise \(\PageIndex{34}\)
\(y=4\)
- Answer
-
horizontal line
Exercise \(\PageIndex{35}\)
\(y=5\)
Exercise \(\PageIndex{36}\)
\(x=−3\)
- Answer
-
vertical line
Exercise \(\PageIndex{37}\)
\(y=−3x+4\)
Exercise \(\PageIndex{38}\)
\(y=−5x+2\)
- Answer
-
slope–intercept
Exercise \(\PageIndex{39}\)
\(x−y=5\)
Exercise \(\PageIndex{40}\)
\(x−y=1\)
- Answer
-
intercepts
Exercise \(\PageIndex{41}\)
\(y=\frac{2}{3} x-1\)
Exercise \(\PageIndex{42}\)
\(y=\frac{4}{5} x-3\)
- Answer
-
slope–intercept
Exercise \(\PageIndex{43}\)
\(y=−3\)
Exercise \(\PageIndex{44}\)
\(y=−1\)
- Answer
-
horizontal line
Exercise \(\PageIndex{45}\)
\(3x−2y=−12\)
Exercise \(\PageIndex{46}\)
\(2x−5y=−10\)
- Answer
-
intercepts
Exercise \(\PageIndex{47}\)
\(y=-\frac{1}{4}x+3\)
Exercise \(\PageIndex{48}\)
\(y=-\frac{1}{3} x+5\)
- Answer
-
slope–intercept
Graph and Interpret Applications of Slope–Intercept
Exercise \(\PageIndex{49}\)
The equation \(P=31+1.75w\) models the relation between the amount of Tuyet’s monthly water bill payment, \(P\), in dollars, and the number of units of water, \(w\), used.
- Find Tuyet’s payment for a month when \(0\) units of water are used.
- Find Tuyet’s payment for a month when \(12\) units of water are used.
- Interpret the slope and \(P\)-intercept of the equation.
- Graph the equation.
Exercise \(\PageIndex{50}\)
The equation \(P=28+2.54w\) models the relation between the amount of Randy’s monthly water bill payment, \(P\), in dollars, and the number of units of water, \(w\), used.
- Find the payment for a month when Randy used \(0\) units of water.
- Find the payment for a month when Randy used \(15\) units of water.
- Interpret the slope and \(P\)-intercept of the equation.
- Graph the equation.
- Answer
-
- \($28\)
- \($66.10\)
- The slope, \(2.54\), means that Randy’s payment, \(P\), increases by \($2.54\) when the number of units of water he used, \(w\), ncreases by \(1\). The \(P\)-intercept means that if the number units of water Randy used was \(0\), the payment would be \($28\).
-
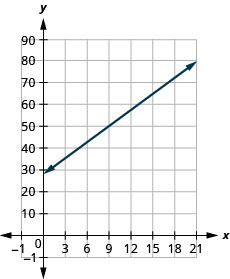
Exercise \(\PageIndex{51}\)
Bruce drives his car for his job. The equation \(R=0.575m+42\) models the relation between the amount in dollars, \(R\), that he is reimbursed and the number of miles, \(m\), he drives in one day.
- Find the amount Bruce is reimbursed on a day when he drives \(0\) miles.
- Find the amount Bruce is reimbursed on a day when he drives \(220\) miles.
- Interpret the slope and \(R\)-intercept of the equation.
- Graph the equation.
Exercise \(\PageIndex{52}\)
Janelle is planning to rent a car while on vacation. The equation \(C=0.32m+15\) models the relation between the cost in dollars, \(C\), per day and the number of miles, \(m\), she drives in one day.
- Find the cost if Janelle drives the car \(0\) miles one day.
- Find the cost on a day when Janelle drives the car \(400\) miles.
- Interpret the slope and \(C\)-intercept of the equation.
- Graph the equation.
- Answer
-
- \($15\)
- \($143\)
- The slope, \(0.32\), means that the cost, \(C\), increases by \($0.32\) when the number of miles driven, \(m\), increases by \(1\). The \(C\)-intercept means that if Janelle drives \(0\) miles one day, the cost would be \($15\).
-
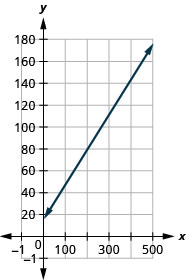
Exercise \(\PageIndex{53}\)
Cherie works in retail and her weekly salary includes commission for the amount she sells. The equation \(S=400+0.15c\) models the relation between her weekly salary, \(S\), in dollars and the amount of her sales, \(c\), in dollars.
- Find Cherie’s salary for a week when her sales were \(0\).
- Find Cherie’s salary for a week when her sales were \(3600\).
- Interpret the slope and \(S\)-intercept of the equation.
- Graph the equation.
Exercise \(\PageIndex{54}\)
Patel’s weekly salary includes a base pay plus commission on his sales. The equation \(S=750+0.09c\) models the relation between his weekly salary, \(S\), in dollars and the amount of his sales, \(c\), in dollars.
- Find Patel’s salary for a week when his sales were \(0\).
- Find Patel’s salary for a week when his sales were \(18,540\).
- Interpret the slope and \(S\)-intercept of the equation.
- Graph the equation.
- Answer
-
- \($750\)
- \($2418.60\)
- The slope, \(0.09\), means that Patel’s salary, \(S\), increases by \($0.09\) for every \($1\) increase in his sales. The \(S\)-intercept means that when his sales are \($0\), his salary is \($750\).
-
Exercise \(\PageIndex{55}\)
Costa is planning a lunch banquet. The equation \(C=450+28g\) models the relation between the cost in dollars, \(C\), of the banquet and the number of guests, \(g\).
- Find the cost if the number of guests is \(40\).
- Find the cost if the number of guests is \(80\).
- Interpret the slope and \(C\)-intercept of the equation.
- Graph the equation.
Exercise \(\PageIndex{56}\)
Margie is planning a dinner banquet. The equation \(C=750+42g\) models the relation between the cost in dollars, \(C\), of the banquet and the number of guests, \(g\).
- Find the cost if the number of guests is \(50\).
- Find the cost if the number of guests is \(100\).
- Interpret the slope and \(C\)-intercept of the equation.
- Graph the equation.
- Answer
-
- \($2850\)
- \($4950\)
- The slope, \(42\), means that the cost, \(C\), increases by \($42\) for when the number of guests increases by \(1\). The \(C\)-intercept means that when the number of guests is \(0\), the cost would be \($750\).
-
Use Slopes to Identify Parallel Lines
In the following exercises, use slopes and \(y\)-intercepts to determine if the lines are parallel.
Exercise \(\PageIndex{57}\)
\(y=\frac{3}{4} x-3 ; \quad 3x-4y=-2\)
Exercise \(\PageIndex{58}\)
\(y=\frac{2}{3} x-1 ; \quad 2x-3y=-2\)
- Answer
-
parallel
Exercise \(\PageIndex{59}\)
\(2x-5y=-3; \quad y=\frac{2}{5} x+1\)
Exercise \(\PageIndex{60}\)
\(3x-4y=-2; \quad y=\frac{3}{4} x-3\)
- Answer
-
parallel
Exercise \(\PageIndex{61}\)
\(2x-4y=6 ; \quad x-2y=3\)
Exercise \(\PageIndex{62}\)
\(6x−3y=9; \quad 2x−y=3\)
- Answer
-
not parallel
Exercise \(\PageIndex{63}\)
\(4x+2y=6 ; \quad 6x+3y=3\)
Exercise \(\PageIndex{64}\)
\(8x+6y=6; \quad 12x+9y=12\)
- Answer
-
parallel
Exercise \(\PageIndex{65}\)
\(x=5 ; \quad x=-6\)
Exercise \(\PageIndex{66}\)
\(x=7 ; \quad x=-8\)
- Answer
-
parallel
Exercise \(\PageIndex{67}\)
\(x=-4 ; \quad x=-1\)
Exercise \(\PageIndex{68}\)
\(x=-3 ; \quad x=-2\)
- Answer
-
parallel
Exercise \(\PageIndex{69}\)
\(y=2; \quad y=6\)
Exercise \(\PageIndex{70}\)
\(y=5; \quad y=1\)
- Answer
-
parallel
Exercise \(\PageIndex{71}\)
\(y=−4; \quad y=3\)
Exercise \(\PageIndex{72}\)
\(y=−1; \quad y=2\)
- Answer
-
parallel
Exercise \(\PageIndex{73}\)
\(x-y=2 ; \quad 2x-2y=4\)
Exercise \(\PageIndex{74}\)
\(4x+4y=8 ; \quad x+y=2\)
- Answer
-
not parallel
Exercise \(\PageIndex{75}\)
\(x-3y=6 ; \quad 2x-6y=12\)
Exercise \(\PageIndex{76}\)
\(5x-2y=11 ; \quad 5x-y=7\)
- Answer
-
not parallel
Exercise \(\PageIndex{77}\)
\(3x-6y=12; \quad 6x-3y=3\)
Exercise \(\PageIndex{78}\)
\(4x-8y=16; \quad x-2y=4\)
- Answer
-
not parallel
Exercise \(\PageIndex{79}\)
\(9x-3y=6; \quad 3x-y=2\)
Exercise \(\PageIndex{80}\)
\(x-5y=10; \quad 5x-y=-10\)
- Answer
-
not parallel
Exercise \(\PageIndex{81}\)
\(7x-4y=8; \quad 4x+7y=14\)
Exercise \(\PageIndex{82}\)
\(9x-5y=4; \quad 5x+9y=-1\)
- Answer
-
not parallel
Use Slopes to Identify Perpendicular Lines
In the following exercises, use slopes and \(y\)-intercepts to determine if the lines are perpendicular.
Exercise \(\PageIndex{83}\)
\(3x-2y=8; \quad 2x+3y=6\)
Exercise \(\PageIndex{84}\)
\(x-4y=8; \quad 4x+y=2\)
- Answer
-
perpendicular
Exercise \(\PageIndex{85}\)
\(2x+5y=3; \quad 5x-2y=6\)
Exercise \(\PageIndex{86}\)
\(2x+3y=5; \quad 3x-2y=7\)
- Answer
-
perpendicular
Exercise \(\PageIndex{87}\)
\(3x-2y=1; \quad 2x-3y=2\)
Exercise \(\PageIndex{88}\)
\(3x-4y=8; \quad 4x-3y=6\)
- Answer
-
not perpendicular
Exercise \(\PageIndex{89}\)
\(5x+2y=6; \quad 2x+5y=8\)
Exercise \(\PageIndex{90}\)
\(2x+4y=3; \quad 6x+3y=2\)
- Answer
-
not perpendicular
Exercise \(\PageIndex{91}\)
\(4x-2y=5; \quad 3x+6y=8\)
Exercise \(\PageIndex{92}\)
\(2x-6y=4; \quad 12x+4y=9\)
- Answer
-
perpendicular
Exercise \(\PageIndex{93}\)
\(6x-4y=5; \quad 8x+12y=3\)
Exercise \(\PageIndex{94}\)
\(8x-2y=7; \quad 3x+12y=9\)
- Answer
-
perpendicular
Self Check
a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
b. After looking at the checklist, do you think you are well-prepared for the next section? Why or why not?




















