1.3: Trigonometric Functions

Learning Objectives

• Convert angle measures between degrees and radians.
• Recognize the triangular and circular definitions of the basic trigonometric functions.
• Write the basic trigonometric identities.
• Identify the graphs and periods of the trigonometric functions.
• Describe the shift of a sine or cosine graph from the equation of the function.

Trigonometric functions are used to model many phenomena, including sound waves, vibrations of strings, alternating electrical current, and the motion of pendulums. In fact, almost any repetitive, or cyclical, motion can be modeled by some combination of trigonometric functions. In this section, we define the six basic trigonometric functions and look at some of the main identities involving these functions.

Radian Measure

To use trigonometric functions, we first must understand how to measure the angles. Although we can use both radians and degrees, radians are a more natural measurement because they are related directly to the unit circle, a circle with radius 1. The radian measure of an angle is defined as follows. Given an angle \(θ\), let \(s\) be the length of the corresponding arc on the unit circle (Figure \(\PageIndex{1}\)). We say the angle corresponding to the arc of length 1 has radian measure 1.

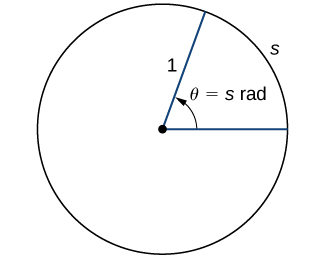
Figure \(\PageIndex{1}\): The radian measure of an angle \(θ\) is the arc length \(s\) of the associated arc on the unit circle. From the center of the unit circle (radius 1), a line segment extends horizontally to the right a point on the edge of the circle and another that extends to another point on the edge of the circle. The curved segment on the edge of the circle that connects the two points at the end of the line segments is labeled \(s\), the arc length. The angle at the center of the circle formed by the two line segments is shown as an arrow pointing counterclockwise, and labeled “\(\theta = s\) radians”.

Since an angle of \(360°\) corresponds to the circumference of a circle, or an arc of length \(2π\), we conclude that an angle with a degree measure of \(360°\) has a radian measure of \(2π\). Similarly, we see that \(180°\) is equivalent to \(\pi\) radians. Table \(\PageIndex{1}\) shows the relationship between common degree and radian values.

Table \(\PageIndex{1}\): Common Angles Expressed in Degrees and Radians

Degrees	Radians	Degrees	Radians
0	0	120	\(2π/3\)
30	\(π/6\)	135	\(3π/4\)
45	\(π/4\)	150	\(5π/6\)
60	\(π/3\)	180	\(π\)
90	\(π/2\)

Converting between Radians and Degrees

1. Express \(225°\) using radians.
2. Express \(5π/3\) rad using degrees.

Solution

Use the fact that \(180\)° is equivalent to \(\pi\) radians as a conversion factor (Table \(\PageIndex{1}\)):

\[1=\dfrac{π \,\mathrm{rad}}{180°}=\dfrac{180°}{π \,\mathrm{rad}}. \nonumber \]

1. \(225°=225°⋅\left(\dfrac{π}{180°}\right)=\left(\dfrac{5π}{4}\right)\) rad
2. \(\dfrac{5π}{3}\) rad = \(\dfrac{5π}{3}\)⋅\(\dfrac{180°}{π}\)=\(300\)°

Exercise \(\PageIndex{1}\)

1. Express \(210°\) using radians.
2. Express \(11π/6\) rad using degrees.

Hint

\(π\) radians is equal to 180°

Answer

1. \(7π/6\)
2. 330°

The Six Basic Trigonometric Functions

Trigonometric functions allow us to use angle measures, in radians or degrees, to find the coordinates of a point on any circle—not only on a unit circle—or to find an angle given a point on a circle. They also define the relationship between the sides and angles of a triangle.

To define the trigonometric functions, first consider the unit circle centered at the origin and a point \(P=(x,y)\) on the unit circle. Let \(θ\) be an angle with an initial side that lies along the positive \(x\)-axis and with a terminal side that is the line segment \(OP\). An angle in this position is said to be in standard position (Figure \(\PageIndex{2}\)). We can then define the values of the six trigonometric functions for \(θ\) in terms of the coordinates \(x\) and \(y\).

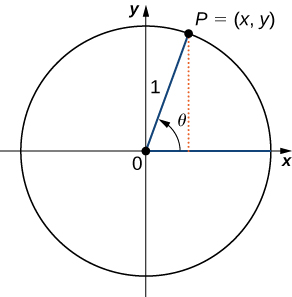
Figure \(\PageIndex{2}\): An angle \(\theta\) is marked on a unit circle in standard position. The point on the edge of the circle corresponding to the angle \(\theta\) is labeled "\(P = (x, y)\)".

Definition: Trigonometric functions

Let \(P=(x,y)\) be a point on the unit circle centered at the origin \(O\). Let \(θ\) be an angle with an initial side along the positive \(x\)-axis and a terminal side given by the line segment \(OP\). The trigonometric functions are then defined as

Table \(\PageIndex{1}\): Definitions of the six trigonometric functions

Trigonometric Function	Reciprocal Trigonometric Function
\(\sin θ=y\)	\(\csc θ=\dfrac{1}{y}\)
\(\cos θ=x\)	\(\sec θ=\dfrac{1}{x}\)
\(\tan θ=\dfrac{y}{x}\)	\(\cot θ=\dfrac{x}{y}\)

If \(x=0, \sec θ\) and \(\tan θ\) are undefined. If \(y=0\), then \(\cot θ\) and \(\csc θ\) are undefined.

We can see that for a point \(P=(x,y)\) on a circle of radius \(r\) with a corresponding angle \(θ\), the coordinates \(x\) and \(y\) satisfy

\[\begin{align} \cos θ &=\dfrac{x}{r} \\ x &=r\cos θ \end{align} \nonumber \]

and

\[\begin{align} \sin θ &=\dfrac{y}{r} \\ y &=r\sin θ. \end{align} \nonumber \]

The values of the other trigonometric functions can be expressed in terms of \(x,y\), and \(r\) (Figure \(\PageIndex{3}\)).

Figure \(\PageIndex{3}\): For a point \(P=(x,y)\) on a circle of radius \(1\) corresponding to the angle \(\theta\) in standard position, the coordinates \(x\) and \(y\) satisfy \(x=r\cos θ\) and \(y=r\sin θ\).

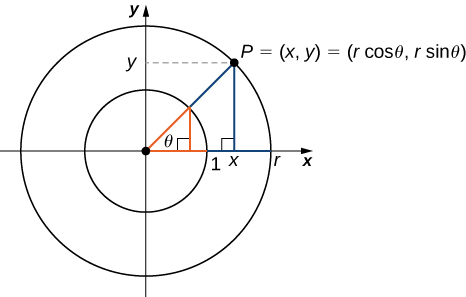
Table \(\PageIndex{2}\) shows the values of sine and cosine at the major angles in the first quadrant. From this table, we can determine the values of sine and cosine at the corresponding angles in the other quadrants. The values of the other trigonometric functions are calculated easily from the values of \(\sin θ\) and \(\cos θ.\)

Table \(\PageIndex{2}\): Values of \(\sin θ\) and \(\cos θ\) at Major Angles \(θ\) in the First Quadrant

\(θ\)θ	\(\sin θ\)	\(\cos θ\)
0	0	1
\(\dfrac{π}{6}\)	\(\dfrac{1}{2}\)	\(\dfrac{\sqrt{3}}{2}\)
\(\dfrac{π}{4}\)	\(\dfrac{\sqrt{2}}{2}\)	\(\dfrac{\sqrt{2}}{2}\)
\(\dfrac{π}{3}\)	\(\dfrac{\sqrt{3}}{2}\)	\(\dfrac{1}{2}\)
\(\dfrac{π}{2}\)	1	0

Example \(\PageIndex{2}\): Evaluating Trigonometric Functions

Evaluate each of the following expressions.

1. \(\sin \left(\dfrac{2π}{3} \right)\)
2. \(\cos \left(−\dfrac{5π}{6} \right)\)
3. \(\tan \left(\dfrac{15π}{4}\right)\)

Solution:

a) On the unit circle, the angle \(θ=\dfrac{2π}{3}\) corresponds to the point \(\left(−\dfrac{1}{2},\dfrac{\sqrt{3}}{2}\right)\). Therefore,

\[ \sin \left(\dfrac{2π}{3}\right)=y=\left(\dfrac{\sqrt{3}}{2}\right). \nonumber \]

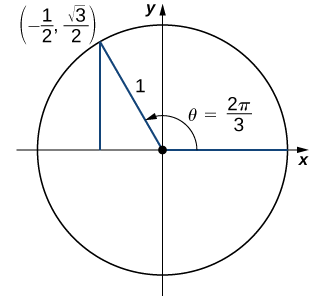
Figure \(\PageIndex{4}\): The angle \(\theta=\frac{2\pi}{3}\) is marked in standard position on the unit circle. The coordinates of the corresponding point on the unit circle are \( (-\frac{1}{2}, \frac{\sqrt{3}}{2}) \).

b) An angle \(θ=−\dfrac{5π}{6}\) corresponds to a revolution in the negative direction, as shown. Therefore,

\[\cos \left(−\dfrac{5π}{6}\right)=x=−\dfrac{\sqrt{3}}{2}. \nonumber \]

Figure \(\PageIndex{5}\): The angle \(\theta=-\frac{5\pi}{6}\) is marked in standard position on the unit circle. The coordinates of the corresponding point on the unit circle are \( (-\frac{\sqrt{3}}{2}, -\frac{1}{2}) \).

c) An angle \(θ\)=\(\dfrac{15π}{4}\)=\(2π\)+\(\dfrac{7π}{4}\). Therefore, this angle corresponds to more than one revolution, as shown. Knowing the fact that an angle of \(\dfrac{7π}{4}\) corresponds to the point \((\dfrac{\sqrt{2}}{2},-\dfrac{\sqrt{2}}{2})\), we can conclude that

\[\tan \left(\dfrac{15π}{4}\right)=\dfrac{y}{x}=−1. \nonumber \]

Figure \(\PageIndex{6}\): The angle \(\theta=\frac{15\pi}{4}\) is marked in standard position on the unit circle. The coordinates of the corresponding point on the unit circle are \( (\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}) \).

Exercise \(\PageIndex{2}\)

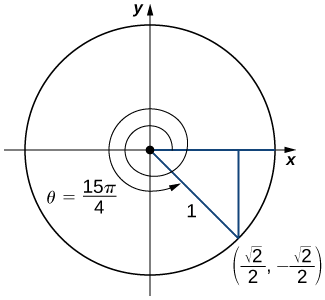
Evaluate \(\cos(3π/4)\) and \(\sin(−π/6)\).

Hint

Look at angles on the unit circle.

Answer

\[\cos(3π/4) = −\sqrt{2}/2\nonumber \]

\[ \sin(−π/6) =−1/2 \nonumber \]

As mentioned earlier, the ratios of the side lengths of a right triangle can be expressed in terms of the trigonometric functions evaluated at either of the acute angles of the triangle. Let \(θ\) be one of the acute angles. Let \(A\) be the length of the adjacent leg, \(O\) be the length of the opposite leg, and \(H\) be the length of the hypotenuse. By inscribing the triangle into a circle of radius \(H\), as shown in Figure \(\PageIndex{4}\), we see that \(A,H\), and \(O\) satisfy the following relationships with \(θ\):

Table \(\PageIndex{2}\): Definitions of the six trigonometric functions as ratios of sides of a triangle

Trigonometric Function	Reciprocal Trigonometric Function
\(\sin θ=\dfrac{O}{H}\)	\(\csc θ=\dfrac{H}{O}\)
\(\cos θ=\dfrac{A}{H}\)	\(\sec θ=\dfrac{H}{A}\)
\(\tan θ=\dfrac{O}{A}\)	\(\cot θ=\dfrac{A}{O}\)

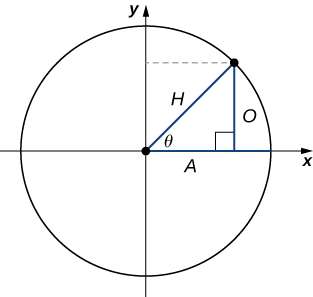
Figure \(\PageIndex{7}\): By inscribing a right triangle in a circle, we can express the ratios of the side lengths in terms of the trigonometric functions evaluated at \(θ\). The angle \(θ\) is marked in standard position and a point corresponding to this angle is marked on the circle. The distance from the origin to this point is marked as "\(H\)" (for hypotenuse), the base of the triangle is marked as "\(A\)" (for adjacent), and the height of the triangle is marked as "\(O\)" (for opposite).

Example \(\PageIndex{3}\): Constructing a Wooden Ramp

A wooden ramp is to be built with one end on the ground and the other end at the top of a short staircase. If the top of the staircase is \(4\) ft from the ground and the angle between the ground and the ramp is to be \(10\)°, how long does the ramp need to be?

Solution

Let \(x\) denote the length of the ramp. In the following image, we see that \(x\) needs to satisfy the equation \(\sin(10°)=4/x\). Solving this equation for \(x\), we see that \(x=4/\sin(10°)\)≈\(23.035\) ft.

Figure \(\PageIndex{8}\): An image of a ramp and a staircase. The ramp starts at a point and increases diagonally upwards and to the right at an angle of \(10°\) for \(x\) feet. At the end of the ramp, which is \(4\) feet off the ground, a staircase descends downwards and to the right.

Exercise \(\PageIndex{3}\)

A house painter wants to lean a \(20\)-ft ladder against a house. If the angle between the base of the ladder and the ground is to be \(60\)°, how far from the house should she place the base of the ladder?

Hint

Draw a right triangle with hypotenuse 20.

Answer

10 ft

Trigonometric Identities

A trigonometric identity is an equation involving trigonometric functions that is true for all angles \(θ\) for which the functions are defined. We can use the identities to help us solve or simplify equations. The main trigonometric identities are listed next.

Trigonometric Identities

Reciprocal identities

\[\tan θ=\dfrac{\sin θ}{\cos θ} \nonumber \]

\[\cot θ=\dfrac{\cos θ}{\sin θ} \nonumber \]

\[\csc θ=\dfrac{1}{\sin θ} \nonumber \]

\[\sec θ=\dfrac{1}{\cos θ} \nonumber \]

Pythagorean identities

\[\begin{align} \sin^2θ+\cos^2θ &=1 \label{py1} \\[4pt] 1+\tan^2θ &=\sec^2θ \\[4pt] 1+\cot^2θ &=\csc^2θ \end{align} \]

Addition and subtraction formulas

\[\sin(α±β)=\sin α\cos β±\cos α \sin β \nonumber \]

\[\cos(α±β)=\cos α\cos β∓\sin α \sin β \nonumber \]

Double-angle formulas

\[\sin(2θ)=2\sin θ\cos θ \label{double1} \]

\[\begin{align} \cos(2θ) &=2\cos^2θ−1 \\[4pt] &=1−2\sin^2θ \\[4pt] &=\cos^2θ−\sin^2θ \end{align} \nonumber \]

Example \(\PageIndex{4}\): Solving Trigonometric Equations

For each of the following equations, use a trigonometric identity to find all solutions.

1. \(1+\cos(2θ)=\cos θ\)
2. \(\sin(2θ)=\tan θ\)

Solution

a) Using the double-angle formula for \(\cos(2θ)\), we see that \(θ\) is a solution of

\[1+\cos(2θ)=\cos θ \nonumber \]

if and only if

\[1+2\cos^2θ−1=\cos θ, \nonumber \]

which is true if and only if

\[2\cos^2θ−\cos θ=0. \nonumber \]

To solve this equation, it is important to note that we need to factor the left-hand side and not divide both sides of the equation by \(\cos θ\). The problem with dividing by \(\cos θ\) is that it is possible that \(\cos θ\) is zero. In fact, if we did divide both sides of the equation by \(\cos θ\), we would miss some of the solutions of the original equation. Factoring the left-hand side of the equation, we see that \(θ\) is a solution of this equation if and only if

\[\cos θ(2\cos θ−1)=0. \nonumber \]

Since \(\cos θ=0\) when

\[θ=\dfrac{π}{2},\dfrac{π}{2}±π,\dfrac{π}{2}±2π,…, \nonumber \]

and \(\cos θ=1/2\) when

\[θ=\dfrac{π}{3},\dfrac{π}{3}±2π,…\mathrm{or}\ θ=−\dfrac{π}{3},−\dfrac{π}{3}±2π,…, \nonumber \]

we conclude that the set of solutions to this equation is

\[θ=\dfrac{π}{2}+nπ,\;θ=\dfrac{π}{3}+2nπ \nonumber \]

and

\[θ=−\dfrac{π}{3}+2nπ,\;n=0,±1,±2,….\nonumber \]

b) Using the double-angle formula for \(\sin(2θ)\) and the reciprocal identity for \(\tan(θ)\), the equation can be written as

\[2\sin θ\cos θ=\dfrac{\sin θ}{\cos θ}.\nonumber \]

To solve this equation, we multiply both sides by \(\cos θ\) to eliminate the denominator, and say that if \(θ\) satisfies this equation, then \(θ\) satisfies the equation

\[2\sin θ \cos^2θ−\sin θ=0. \nonumber \]

However, we need to be a little careful here. Even if \(θ\) satisfies this new equation, it may not satisfy the original equation because, to satisfy the original equation, we would need to be able to divide both sides of the equation by \(\cos θ\). However, if \(\cos θ=0\), we cannot divide both sides of the equation by \(\cos θ\). Therefore, it is possible that we may arrive at extraneous solutions. So, at the end, it is important to check for extraneous solutions. Returning to the equation, it is important that we factor \(\sin θ\) out of both terms on the left-hand side instead of dividing both sides of the equation by \(\sin θ\). Factoring the left-hand side of the equation, we can rewrite this equation as

\[\sin θ(2\cos^2θ−1)=0. \nonumber \]

Therefore, the solutions are given by the angles \(θ\) such that \(\sin θ=0\) or \(\cos^2θ=1/2\). The solutions of the first equation are \(θ=0,±π,±2π,….\) The solutions of the second equation are \(θ=π/4,(π/4)±(π/2),(π/4)±π,….\) After checking for extraneous solutions, the set of solutions to the equation is

\[θ=nπ \nonumber \]

and

\[θ=\dfrac{π}{4}+\dfrac{nπ}{2} \nonumber \]

with \(n=0,±1,±2,….\)

Exercise \(\PageIndex{4}\)

Find all solutions to the equation \(\cos(2θ)=\sin θ.\)

Hint

Use the double-angle formula for cosine (Equation \ref{double1}).

Answer

\(θ=\dfrac{3π}{2}+2nπ,\dfrac{π}{6}+2nπ,\dfrac{5π}{6}+2nπ\)

for \(n=0,±1,±2,…\).

Example \(\PageIndex{5}\): Proving a Trigonometric Identity

Prove the trigonometric identity \(1+\tan^2θ=\sec^2θ.\)

Solution:

We start with the Pythagorean identity (Equation \ref{py1})

\[\sin^2θ+\cos^2θ=1. \nonumber \]

Dividing both sides of this equation by \(\cos^2θ,\) we obtain

\[\dfrac{\sin^2θ}{\cos^2θ}+1=\dfrac{1}{\cos^2θ}. \nonumber \]

Since \(\sin θ/\cos θ=\tan θ\) and \(1/\cos θ=\sec θ\), we conclude that

\[\tan^2θ+1=\sec^2θ. \nonumber \]

Exercise \(\PageIndex{5}\)

Prove the trigonometric identity \(1+\cot^2θ=\csc^2θ.\)

Answer

Divide both sides of the identity \(\sin^2θ+\cos^2θ=1\) by \(\sin^2θ\).

Graphs and Periods of the Trigonometric Functions

We have seen that as we travel around the unit circle, the values of the trigonometric functions repeat. We can see this pattern in the graphs of the functions. Let \(P=(x,y)\) be a point on the unit circle and let \(θ\) be the corresponding angle . Since the angle \(θ\) and \(θ+2π\) correspond to the same point \(P\), the values of the trigonometric functions at \(θ\) and at \(θ+2π\) are the same. Consequently, the trigonometric functions are periodic functions. The period of a function \(f\) is defined to be the smallest positive value \(p\) such that \(f(x+p)=f(x)\) for all values \(x\) in the domain of \(f\). The sine, cosine, secant, and cosecant functions have a period of \(2π\). Since the tangent and cotangent functions repeat on an interval of length \(π\), their period is \(π\) (Figure \(\PageIndex{9}\)).

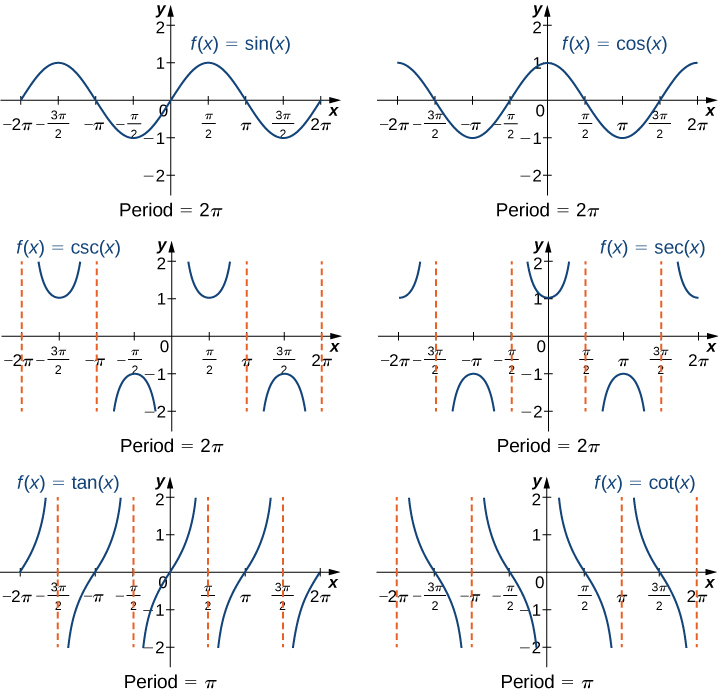
Figure \(\PageIndex{9}\): The six trigonometric functions are periodic. Each graph has an \(x\)-axis that runs from \(-2\pi\) to \(2\pi\) and a \(y\)-axis that runs from \(-2\) to \(2\). (a) The graph of \(f(x) = \sin(x)\) has a sinusoidal shape. It starts at the point \((-2\pi, 0)\) and increases until the point \((-(3\pi)/2, 1)\). After this point, the function decreases until the point \((-(\pi/2), -1)\). After this point, the function increases until the point \((\pi/2, 1)\). After this point, the function decreases until the point \((3\pi/2), -1)\). After this point, the function begins to increase again. The \(x\) intercepts shown on the graph are at the points \((-2\pi, 0), (-\pi, 0), (0, 0), (\pi, 0), (2\pi, 0)\). The \(y\)-intercept is at the origin. (b) The graph of \(f(x) = \cos(x)\) is also a sinusoidal function. The graph of \(f(x) = \cos(x)\) can be obtained from the graph of \(f(x) = \sin(x)\) by shifting the graph \(\pi/2\) units to the left. The \(x\) intercepts shown on the graph are at the points \((-(3\pi/2), 0), (-\pi/2, 0), (\pi/2, 0), ((3\pi/2), 0)\). The \(y\)-intercept is at the point \((0, 1)\). (c) The graph of \(f(x) = \csc(x)\) has vertical asymptotes at \(x=0\), \(x=\pm\pi\), \(x=\pm2\pi\), ... Between the \(x = -2\pi\) and \(x = -\pi\) asymptotes, the function looks like an upward facing “U”, with a minimum at the point \((-(3\pi/2), 1)\). Between the \(x = -\pi\) and \(x = 0\) asymptotes, the function looks like a downward facing “U”, with a maximum at the point \((-\pi/2, -1)\). Due to the periodic nature of the graph, it continues like this with period \(2\pi\). (d) The graph of \(f(x) = \sec(x)”\) has vertical asymptotes at \(x=\pm\pi/2\), \(x=\pm 3\pi/2\), ... The graph of \(f(x) = \sec(x)\) can be obtained from the graph of \(f(x) = \csc(x)\) by shifting the graph \(\pi/2\) units to the left. (e) The graph of \(f(x) = \tan(x)”\) has vertical asymptotes at \(x=\pm\pi/2\), \(x=\pm 3\pi/2\), ... In between all of the vertical asymptotes, the function is always increasing but it never touches the asymptotes. The x intercepts on this graph occur at the points \((-2\pi, 0), (-\pi, 0), (0, 0), (\pi, 0), (2 \pi, 0)\). The \(y\)-intercept is at the origin. (f) The graph of \(f(x) = \cot(x)\) has vertical asymptotes at \(x=0\), \(x=\pm\pi\), \(x=\pm2\pi\), ... In between all of the vertical asymptotes, the function is always decreasing but it never touches the asymptotes. The \(x\)-intercepts on this graph occur at the points \((-3\pi/2, 0), (-\pi/2, 0), (\pi/2, 0), and (3 \pi/2), 0)\) and there is no \(y\)-intercept.

Just as with algebraic functions, we can apply transformations to trigonometric functions. In particular, consider the following function:

\[f(x)=A\sin(B(x−α))+C. \nonumber \]

In Figure \(\PageIndex{6}\), the constant \(α\) causes a horizontal or phase shift. The factor \(B\) changes the period. This transformed sine function will have a period \(2π/|B|\). The factor \(A\) results in a vertical stretch by a factor of \(|A|\). We say \(|A|\) is the “amplitude of \(f\).” The constant \(C\) causes a vertical shift.

Figure \(\PageIndex{6}\): A graph of a general sine function of the form \(f(x) = A\sin(B(x - \alpha)) + C\). Along the \(y\)-axis, there are 3 values are marked - starting from the bottom and moving up - “\(C - A, C, C + A\)”. The graph's range is \([C-A, C+A]\)The distance from the origin to “\(C\)” is labeled “vertical shift”. The distance from “\(C - A\)” to “\(C\)” and the distance from “\(C\)” to “\(C + A\)” is “\(A\)”, which is labeled “amplitude”. On the \(x\)-axis, the value “\(\alpha\)” is marked, and the distance between the origin and “\(\alpha\)” is labeled “horizontal shift”. The distance between two successive minimum values of the function is “\( \frac{2\pi}{|B|}\)” is labeled the period.

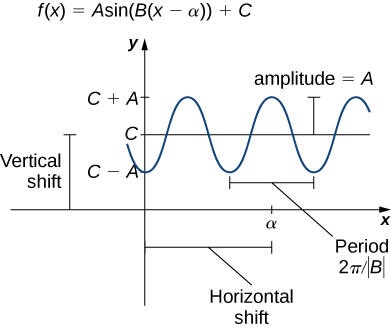
Notice in Figure \(\PageIndex{6}\) that the graph of \(y=\cos x\) is the graph of \(y=\sin x\) shifted to the left \(π/2\) units. Therefore, we can write

\[\cos x=\sin(x+π/2). \nonumber \]

Similarly, we can view the graph of \(y=\sin x\) as the graph of \(y=\cos x\) shifted right \(π/2\) units, and state that \(\sin x=\cos(x−π/2).\)

A shifted sine curve arises naturally when graphing the number of hours of daylight in a given location as a function of the day of the year. For example, suppose a city reports that June 21 is the longest day of the year with 15.7 hours and December 21 is the shortest day of the year with 8.3 hours. It can be shown that the function

\[h(t)=3.7\sin \left(\dfrac{2π}{365}(x−80.5)\right)+12 \nonumber \]

is a model for the number of hours of daylight \(h\) as a function of day of the year \(t\) (Figure \(\PageIndex{7}\)).

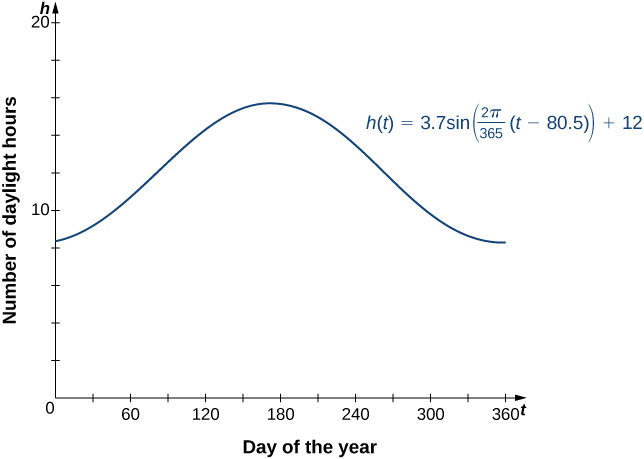
Figure \(\PageIndex{7}\): The hours of daylight as a function of day of the year can be modeled by a shifted sine curve. The horizontal axis runs from \(0\) to \(365\) and is labeled “\(t\)|, representing "Day of the year”. The vertical axis runs from \(0\) to \(20\) and is labeled “\(h\)", representing "Number of daylight hours”. The graph is of the function \(h(t) = 3.7\sin(\frac{2\pi}{365})(t - 80.5)) + 12”, which is a wave function. The function starts at the approximate point \((0, 8.4)\) and begins increasing until the approximate point \((182.5, 15.6)\). After this point, the function decreases until the approximate point \((365, 8.4)\). After this point, the function begins increasing again.

Example \(\PageIndex{6}\): Sketching the Graph of a Transformed Sine Curve

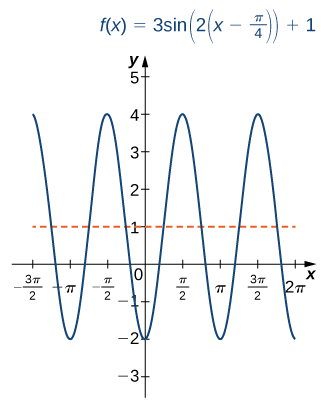
Sketch a graph of \(f(x)=3\sin(2(x−\frac{π}{4}))+1.\)

Solution

This graph is a phase shift of \(y=\sin (x)\) to the right by \(π/4\) units, followed by a horizontal compression by a factor of 2, a vertical stretch by a factor of 3, and then a vertical shift by 1 unit. The period of \(f\) is \(π\).

Figure \(\PageIndex{8}\): The graph of \(f(x)=3\sin(2(x-\frac{\pi}{4}))+1\). The \(x\)-axis runs from \(-\frac{3\pi}{2} to \(2\pi\) and the \(y\)-axis runs from \(-3\) to \(5\). The graph is a wave function that starts decreasing from the point \((\(-\frac{3\pi}{2},4)\) until it hits the point \((-\pi, -2)\). At this point, the function begins increasing until it hits the point \((-\frac{\pi}{2}, 4). After this point, the function begins decreasing until it hits the point \((0, -2)\). After this point, the function increases until it hits the point \((\frac{\pi}{2}, 4)\). After this point, the function decreases until it hits the point \((\pi, -2)\). After this point, the function increases until it hits the point \((\frac{3\pi}{2}), 4)\). After this point, the function decreases again.

Exercise \(\PageIndex{6}\)

Describe the relationship between the graph of \(f(x)=3\sin(4x)−5\) and the graph of \(y=\sin(x)\).

Hint

The graph of \(f\) can be sketched using the graph of \(y=\sin(x)\) and a sequence of three transformations.

Answer

To graph \(f(x)=3\sin(4x)−5\), the graph of \(y=\sin(x)\) needs to be compressed horizontally by a factor of 4, then stretched vertically by a factor of 3, then shifted down 5 units. The function \(f\) will have a period of \(π/2\) and an amplitude of 3.

Key Concepts

• Radian measure is defined such that the angle associated with the arc of length 1 on the unit circle has radian measure 1. An angle with a degree measure of \(180\)° has a radian measure of \(\pi\) rad.
• For acute angles \(θ\),the values of the trigonometric functions are defined as ratios of two sides of a right triangle in which one of the acute angles is \(θ\).
• For a general angle \(θ\), let \((x,y)\) be a point on a circle of radius \(r\) corresponding to this angle \(θ\). The trigonometric functions can be written as ratios involving \(x\), \(y\), and \(r\).
• The trigonometric functions are periodic. The sine, cosine, secant, and cosecant functions have period \(2π\). The tangent and cotangent functions have period \(π\).

Key Equations

• Generalized sine function

\(f(x)=A \sin(B(x−α))+C\)

Glossary

Periodic function

A function is periodic if it has a repeating pattern as the values of \(x\) move from left to right

Radians

For a circular arc of length \(s\) on a circle of radius 1, the radian measure of the associated angle \(θ\) is \(s\)

Trigonometric functions

Functions of an angle defined as ratios of the lengths of the sides of a right triangle

Trigonometric identity

An equation involving trigonometric functions that is true for all angles \(θ\) for which the functions in the equation are defined