7.3: Inverse Trigonometric Functions

Last updated
Save as PDF

Page ID: 212065

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\dsum}{\displaystyle\sum\limits} $

$ \newcommand{\dint}{\displaystyle\int\limits} $

$ \newcommand{\dlim}{\displaystyle\lim\limits} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

We now turn our attention to the inverse trigonometric functions, their properties and their graphs, focusing on properties and techniques needed to investigate derivatives and integrals of these functions. We will concentrate on the inverse sine and inverse tangent functions, the two inverse trigonometric functions that arise most often in calculus.

Inverse Sine: Solving $k = \sin(x)$ for $x$

It is straightforward to solve the equation $3 = e^x$:

$A blue graph of y=e^x in the first quadrant, A horizontal dashed-black line segment extends from (0,3) over to the blue curve, and a vertical dashed-black line segment extends down from that point to a place on the x-axis marked '?.'.png$

Simply apply the natural logarithm function, the inverse of the exponential function $e^x$, to each side of the equation to get $\ln( 3 ) = \ln\left(e^x\right) = x$. Because the function $f(x) = e^x$ is one-to-one, the equation $3 = e^x$ has only the one solution $x = \ln(3) \approx 1.1$.

The solution of the equation $0.5 = \sin(x)$ presents more difficulties. As the figure below illustrates:

$A blue graph of y=sin(x) from x=-pi to x=pi. A dashed-black horizontal line segment extends rightward from (0,0.5), intersecting the blue curve in four places marked by red dots.$

the function $f(x) = \sin(x)$ is not one-to-one: its graph reflected about the line $y=x$:

$A blue graph of the curve x=sin(y) for y between =pi and 3pi, with the section with between -pi/2 and pi/2 shaded red.$

is not the graph of a function. Sometimes, however, it is necessary to “undo” the sine function, and we can do so by restricting its domain to the interval $\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$. For $-\frac{\pi}{2} \leq x \leq \frac{\pi}{2}$, the function $f(x) = \sin(x)$ is one-to-one and has an inverse function — and the graph of the inverse function

$A red graph of y=arcsin(x).$

is the reflection about the line $y = x$ of the (restricted) graph of $y = \sin(x)$.

Caution

Many textbooks — and most calculators — use the notation $\sin^{-1}(x)$ for $\arcsin(x)$. You must be very careful to never interpret $\sin^{-1}(x)$ to mean:\[\left(\sin(x)\right)^{-1} = \frac{1}{\sin(x)} =\csc(x)\]We avoid the $\sin^{-1}(x)$ notation for this reason and suggest that you do as well.

We call this inverse of the (restricted) sine function the arcsine and denote it $\arcsin(x)$. The name “arcsine” comes from the unit-circle definition of the sine function. On the unit circle:

$A blue graph of the unit circle x^2+y^2=1, with a black dot on the circle in the first quadrant labeled '(cos(theta),sin(theta)). A dahed-black vertical line segment extends fomr the dot down to a point on the horizontal axis marked 'x.' The portion of the circle from (1,0) to the black dot in the first quadrant is shaded red and labeled 'theta.'$

if $\theta$ is the length of the arc whose sine is $x$, then $\sin(\theta) = x$ and $\theta = \arcsin(x)$. Using the right-triangle definition of sine:

$A right triangle with hypotenuse 1 and height x. A caption reads: sin(theta)=x, theta=arcsin(x).$

$\theta$ represents an angle whose sine is $x$.

Definition: Inverse Sine

For $-1 \leq x \leq 1$ and $-\frac{\pi}{2} \leq y \leq \frac{\pi}{2}$:\[y = \arcsin(x) \iff x = \sin(y)\]The domain of $\arcsin(x)$ is $\left[-1, 1\right]$ and its range is $\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$.

The (restricted) sine function and the arcsine are inverses of each other:
\begin{align*}
-1 \leq x \leq 1 \ &\Rightarrow \ \sin\left(\arcsin(x)\right) = x\\
-\frac{\pi}{2} \leq y \leq \frac{\pi}{2} \ &\Rightarrow \ \arcsin\left(\sin(y)\right) = y\end{align*}

Right Triangles and Arcsine

For the right triangle shown below:

$On the left is a right triangle with base 4, height 3 and hypotenuse 5; the angle opposite the side of length 3 has measure theta. On the right: sin(theta) = 3/5, theta=(arcsin(3/5), theta approximately equal to 0.6435.$

$\sin(\theta) = \frac{\mbox{opposite}}{\mbox{hypotenuse}} = \frac35$ so $\theta = \arcsin\left(\frac35\right)$. It is possible to evaluate other trigonometric functions (such as cosine and tangent) of an angle expressed as an arcsine without explicitly solving for the value of the angle. For example:
\begin{align*}\cos\left(\arcsin\left(\frac35\right)\right) &= \cos(\theta) = \frac{\mbox{adjacent}}{\mbox{hypotenuse}} = \frac45 \\
\tan\left(\arcsin\left(\frac35\right)\right) &= \tan(\theta) = \frac{\mbox{opposite}}{\mbox{adjacent}} = \frac34\end{align*}
Once you know the sides of the right triangle, you can compute the values of the other trigonometric functions using their standard right-triangle definitions:

\begin{align*}
\sin(\theta) &= \frac{\mbox{opposite}}{\mbox{hypotenuse}}\\
\csc(\theta) &= \frac{1}{\sin(\theta)} = \frac{\mbox{hypotenuse}}{\mbox{opposite}}
\end{align*}

\begin{align*}
\cos(\theta) &= \frac{\mbox{adjacent}}{\mbox{hypotenuse}}\\
\sec(\theta) &= \frac{1}{\cos(\theta)} = \frac{\mbox{hypotenuse}}{\mbox{adjacent}}
\end{align*}

\begin{align*}
\tan(\theta) &= \frac{\mbox{opposite}}{\mbox{adjacent}}\\
\cot(\theta) &= \frac{1}{\tan(\theta)} = \frac{\mbox{adjacent}}{\mbox{opposite}}
\end{align*}

If you are given an angle $\theta$ as the arcsine of a number, but not given the sides of a right triangle, you can construct your own triangle with the given angle: select values for the opposite side and hypotenuse so the ratio $\frac{\mbox{opposite}}{\mbox{hypotenuse}}$ is the value whose arcsine we want: $\displaystyle \arcsin\left(\frac{\mbox{opposite}}{\mbox{hypotenuse}}\right)$. You can calculate the length of the third (“adjacent”) side using the Pythagorean Theorem.

Example $\PageIndex{1}$

Determine the lengths of the sides of a right triangle so one angle is $\theta = \arcsin\left(\frac{5}{13}\right)$. Use the triangle to determine the values of $\tan\left(\arcsin\left(\frac{5}{13}\right)\right)$ and $\csc\left(\arcsin\left(\frac{5}{13}\right)\right)$.

Solution

We want the sine of $\theta$, the ratio $\frac{\mbox{opposite}}{\mbox{hypotenuse}}$, to be $\frac{5}{13}$ so we can choose the opposite side to be $5$ and the hypotenuse to be $13$:

$A right triangle with base 12, height 5 and hypotenuse 13; the angle opposite the side of length 5 has measure theta. Belows this is the equation sin(theta) = 5/13.$

Then $\sin(\theta) = \frac{5}{13}$, as desired. Using the Pythagorean Theorem, the length of the adjacent side is $\sqrt{13^2 - 5^2} = 12$. So:
\begin{align*}
\tan(\theta) &= \tan\left(\arcsin\left(\frac{5}{13}\right)\right) = \frac{\mbox{opposite}}{\mbox{adjacent}} = \frac{5}{12}\\
\csc(\theta) &= \csc\left(\arcsin\left(\frac{5}{13}\right)\right) = \frac{1}{\sin\left(\arcsin\left(\frac{5}{13}\right)\right)} = \frac{1}{\frac{5}{13}} = \frac{13}{5}
\end{align*}
Any choice of values for the opposite side and the hypotenuse will work (for example opposite $= 500$ and hypotenuse $=1300$), as long as the ratio of the opposite side to the hypotenuse is $\frac{5}{13}$.

Practice $\PageIndex{1}$

Determine the lengths of the sides of a right triangle so one angle is $\theta = \arcsin\left(\frac{6}{11}\right)$. Use the triangle to determine the values of $\tan\left(\arcsin\left(\frac{6}{11}\right)\right)$, $\csc\left(\arcsin\left(\frac{6}{11}\right)\right)$ and $\cos\left(\arcsin\left(\frac{6}{11}\right)\right)$.

Answer

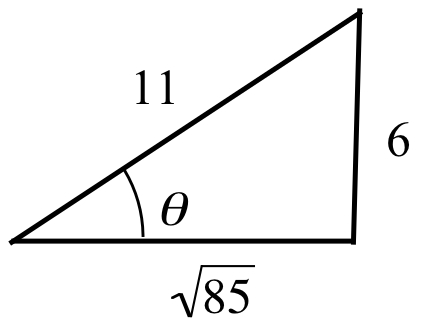
$A right triangle with base sqrt(85), height 6 and hypotenuse 11. The angle between base and hypotenuse has measure theta.$

With hypotenuse $11$ and opposite side $6$, the adjacent side must have length $\sqrt{11^2-6^2} = \sqrt{85}$, so:
\begin{align*}
\tan\left(\arcsin\left(\frac{6}{11}\right)\right) &= \frac{6}{\sqrt{85}}\\
\csc\left(\arcsin\left(\frac{6}{11}\right)\right) &= \frac{11}{6}\\
\cos\left(\arcsin\left(\frac{6}{11}\right)\right) &= \frac{\sqrt{85}}{11}
\end{align*}

Example $\PageIndex{2}$

Determine the lengths of the sides of a right triangle so one angle is $\theta = \arcsin(x)$. Use the triangle to determine the values of $\tan\left(\arcsin(x)\right)$ and $\cos\left(\arcsin(x)\right)$.

Solution

We want the sine of $\theta$, the ratio $\frac{\mbox{opposite}}{\mbox{hypotenuse}}$, to be $x$ so we can choose the opposite side to be $x$ and the hypotenuse to be $1$:

$A right triangle with height x and hypotenuse 1. Below this is the equation theta = arcsin(x).$

Then $\sin(\theta) = \frac{x}{1} = x$ and, using the Pythagorean Theorem, the length of the adjacent side is $\sqrt{1 - x^2}$ so that:
\begin{align*}
\tan\left(\arcsin(x)\right) &= \frac{\mbox{opposite}}{\mbox{adjacent}} = \frac{x}{\sqrt{1-x^2}}\\
\cos\left(\arcsin(x)\right) &= \frac{\mbox{adjacent}}{\mbox{hypotenuse}} = \frac{\sqrt{1-x^2}}{1} = \sqrt{1-x^2}
\end{align*}
Other choices for the lengths of the opposite side and hypotenuse, such as $3x$ and $3$, will work, but $x$ and $1$ are the simplest choices.

Practice $\PageIndex{2}$

Evaluate $\sec\left(\arcsin( x )\right)$ and $\csc\left(\arcsin( x )\right)$.

Answer

$A right triangle with base sqrt(1-x^2), height x and hypotenuse 1. The angle between base and hypotenuse has measure theta.$

With hypotenuse $1$ and opposite side $x$, the adjacent side must have length $\sqrt{1^2-x^2} = \sqrt{1-x^2}$, so:
\begin{align*}
\sec\left(\arcsin\left(x\right)\right) &= \frac{1}{\sqrt{1-x^2}}\\
\csc\left(\arcsin\left(x\right)\right) &= \frac{1}{x}
\end{align*}

Inverse Tangent: Solving $k = \tan(x)$ for $x$

The equation $0.5 = \tan(x)$:

$A blue graph of y=tan(x) from x=-pi to x=2.5pi with dashed-black vertical asymptotes at x=-0.5pi, 0.5pi and 1.5pi, and a dashed-black horizontal line at y=0.5.$

has many solutions: the function $f(x) = \tan(x)$ is not one-to-one, and its graph reflected across the line $y=x$:

$A blue graph of x=tan(y) from y=-pi to y=2.5pi with dashed-black horizontal asymptotes at y=-0.5pi, 0.5pi and 1.5pi The branch passing through the origin is shaded red.$

is not the graph of a function. If, however, we restrict the domain of the tangent function to the interval $\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$, then the restricted $f(x) = \tan(x)$ is one-to-one and has an inverse function. The graph of this inverse tangent function:

$A red graph of y=arctan(x) with horizontal dasehd-black lines at y=pi/2 and y=-pi/2.$

is the reflection about the line $y = x$ of the (restricted) graph of $y = \tan(x)$. We call this inverse of the (restricted) tangent function the arctangent and denote it $\arctan(x)$. For $x>0$, the number $\arctan(x)$ is the length of the arc on the unit circle whose tangent is $x$, and $\arctan(x)$ is the angle whose tangent is $x$: $\tan\left(\arctan(x)\right) = x$.

Caution

Many textbooks — and most calculators — use the notation $\tan^{-1}(x)$ for $\arctan(x)$. You must be very careful to never interpret $\tan^{-1}(x)$ to mean:\[\left(\tan(x)\right)^{-1} = \frac{1}{\tan(x)} =\cot(x)\]We avoid the $\tan^{-1}(x)$ notation for this reason and suggest that you do as well.

Definition: Inverse Tangent

For all $x$ and $-\frac{\pi}{2} < y < \frac{\pi}{2}$:\[y = \arctan(x) \iff x = \tan(y)\]The domain of $\arctan(x)$ is $\left(-\infty, \infty\right)$ and its range is $\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$.

The (restricted) tangent function and the arctangent are inverses:
\begin{align*}
-\infty < x < \infty \ &\Rightarrow \ \tan\left(\arctan(x)\right) = x\\
-\frac{\pi}{2} < y < \frac{\pi}{2} \ &\Rightarrow \ \arctan\left(\tan(y)\right) = y \end{align*}

Right Triangles and Arctangent

For the right triangle in the figure below:

$On the left is a right triangle with base 2, height 3 and hypotenuse sqrt(13). On the right: tan(theta) = 3/2, theta = arctan(3/2), theta approximately equal to 0.9828.$

$\tan(\theta) = \frac{\mbox{opposite}}{\mbox{adjacent}} = \frac32$ so that $\theta = \arctan\left(\frac32\right)$, hence:
\begin{align*}
\sin\left(\arctan\left(\frac32\right)\right) &= \sin(\theta) = \frac{\mbox{opposite}}{\mbox{hypotenuse}} = \frac{3}{\sqrt{13}} \approx 0.832\\
\cot\left(\arctan\left(\frac32\right)\right) &= \frac{1}{\tan\left(\arctan\left(\frac32\right)\right)} = \frac{1}{\frac32} = \frac23 \approx 0.667
\end{align*}

Practice $\PageIndex{3}$

Determine the lengths of the sides of a right triangle so that one angle is $\theta = \arctan\left(\frac34\right)$, then use the triangle to determine the values of $\sin\left(\arctan\left(\frac34\right)\right)$, $\cot\left(\arctan\left(\frac34\right)\right)$ and $\cos\left(\arctan\left(\frac34\right)\right)$.

Answer

$A right triangle with base 4, height 3 and hypotenuse 5. The angle between base and hypotenuse has measure theta.$

With opposite side $3$ and adjacent side $4$, the hypotenuse must have length $\sqrt{3^2+4^2} = \sqrt{25} = 5$, so:
\begin{align*}
\sin\left(\arctan\left(\frac{3}{4}\right)\right) &= \frac{3}{5}\\
\cot\left(\arctan\left(\frac{3}{4}\right)\right) &= \frac{4}{3}\\
\cos\left(\arctan\left(\frac{3}{4}\right)\right) &= \frac{4}{5}
\end{align*}

Example $\PageIndex{3}$

On a wall 8 feet in front of you, the lower edge of a 5-foot-tall painting rests 2 feet above your eye level:

$A human head on the far left with a horizontal black line segment extending to the right from the eyeline of the head. A double arrows indicates the length of the line segment is 8 ft. Extending up from and perpedicular to the horizontal segment is a vertical segment. Double arrows indicate a distance of 2 ft and then a height of 5ft above that corresponding to a vertical blue line segment. Dashed-black line segments extend from the eyeball of the head to the bottom and top of the blue line segment. Black arcs indicate that the angle between the horizontal and the lower dashed segment is alpha, and that the angle between the horizontal and the upper dashed segment is beta. A red arc indicate the angle between the dashed segments is theta. A caption reads: theta = viewing angle.$

Represent your viewing angle $\theta$ using arctangents.

Solution

The viewing angle $\alpha$ to the bottom of the painting satisfies:\[\tan(\alpha) = \frac{\mbox{opposite}}{\mbox{adjacent}} = \frac28 \Rightarrow \alpha = \arctan\left(\frac14\right)\]Similarly, the angle $\beta$ to the top of the painting satisfies:\[\tan(\beta) = \frac{\mbox{opposite}}{\mbox{adjacent}} = \frac78 \Rightarrow \alpha = \arctan\left(\frac78\right)\]The viewing angle $\theta$ for the painting is therefore:\[\theta = \beta - \alpha = \arctan\left(\frac78\right) - \arctan\left(\frac14\right) \approx 0.719 - 0.245 = 0.474\]or about $27^{\circ}$.

Practice $\PageIndex{4}$

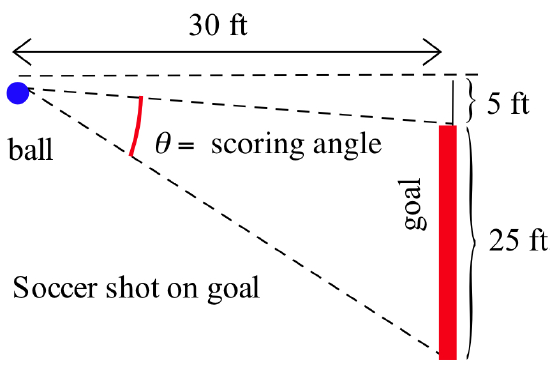
Determine the scoring angle for the soccer player in the figure below:

$A blue dot labeled 'ball' at the upper left is the left endpoint of a dashed-black horizontal line segment with a double arrows indicating its length is 30 ft. From the right endpoint of the horizontal segment, a sold-black line segment extends down and perpendiculr, with a breace indicating its height is 5 ft. Beyond that, a thin red rectangle labeled 'goal' extends further down, with a brace indicating its height it 25 ft. Dashed-black line segments extend from the ball to the top and bottom points of the goal, with the angle between these dashed segments indicated by a red arc labeled 'theta = scoring angle.' A caption reads: Soccer shot on goal.$

Answer: $\tan(\alpha) = \frac{5}{30} = \frac16$ so $\alpha = \arctan\left(\frac16\right) \approx 0.165$ (or about $9.46^{\circ}$). Likewise, $\tan( \alpha + \theta ) = \frac{30}{30} = 1$ so $\alpha + \theta = \arctan(1) =\frac{\pi}{4} \approx 0.785$ (or $45^{\circ}$). Finally:\[\theta = \left( \alpha + \theta \right) - \alpha \approx 0.785 - 0.165 = 0.62\]or about $35.54^{\circ}$.

Example $\PageIndex{4}$

Determine the lengths of the sides of a right triangle so that one angle is $\theta = \arctan(x)$, then use the triangle to determine the values of $\sin\left(\arctan( x )\right)$ and $\cos\left(\arctan( x )\right)$.

Solution

We want the tangent of $\theta$ (the ratio of opposite to adjacent) to be $x$, so we can choose the opposite side to be $x$ and the adjacent side to be $1$:

$A right triangle with height x and base 1. Below this is the equation theta = arctan(x).$

Then $\tan(\theta) = \frac{x}{1} = x$ and, using the Pythagorean Theorem, the length of the hypotenuse is $\sqrt{1 + x^2}$ so that:
\begin{align*}
\sin\left(\arctan( x )\right) &= \frac{\mbox{opposite}}{\mbox{hypotenuse}} = \frac{x}{\sqrt{1 + x^2}}\\
\cos\left(\arctan( x )\right) &= \frac{\mbox{adjacent}}{\mbox{hypotenuse}} = \frac{1}{\sqrt{1 + x^2}}
\end{align*}
We could have chosen other values for the opposite and adjacent sides (such as $x^2$ and $x$), but $x$ and $1$ provide the simplest option.

Practice $\PageIndex{5}$

Evaluate $\sec\left(\arctan(x)\right)$ and $\cot\left(\arctan(x)\right)$.

Answer

$A right triangle with base 1, height x and hypotenuse sqrt(1+x^2). The angle between base and hypotenuse has measure theta.$

With opposite side $x$ and adjacent side $1$, the hypotenuse must have length $\sqrt{1^2+x^2} = \sqrt{1+x^2}$, so:
\begin{align*}
\sec\left(\arctan\left(x\right)\right) &= \frac{1}{\sqrt{1+x^2}}\\
\cot\left(\arctan\left(x\right)\right) &= \frac{1}{x}
\end{align*}

Inverse Secant: Solving $k = \sec(x)$ for $x$

The equation $2 = \sec(x)$:

$A blue graph of y=sec(x) from x=-pi to x=2.5pi, with the portion between x=0 and x=pi shaded red, along with dashed-black vertical asymptotes at x=-pi/2, pi/2 and 3pi/2, as well as dashed-black tangent lines at y=1 y=-1.$

has many solutions, but we can create an inverse function for secant — much the same way we did for sine and tangent — by suitably restricting the domain of the secant function so that it becomes a one-to-one function:

$A red graph of y=sec(x) from x=0 to x=pi with dashed-black vertical lines at x=pi/2 and pi, as well as a dashed-black tangent line at y=-1.$

The figure above shows the restriction $0 \leq x \leq \pi$ ($x \neq \frac{\pi}{2}$), which results in a one-to-one function that has an inverse. The graph of the inverse function:

$A red graph of x=sec(y) from y=0 to y=pi with dashed-black horizontal lines at y=pi/2 and pi, as well as dashed-black tangent lines at y=-1 and 1.$

is the reflection about the line $y = x$ of the (restricted) graph of $y = \sec(x)$. We call this inverse of the (restricted) secant function the arcsecant and denote it $\mbox{arcsec}(x)$.

Definition: Inverse Secant

If $\left| x \right| \geq 1$ and $0 \leq y \leq \pi$ with $y \neq \frac{\pi}{2}$:\[y = \mbox{arcsec}(x) \iff x = \sec(y)\]The domain of $\mbox{arcsec}(x)$ is $(-\infty, -1]\cup[1,\infty)$ and the range of $\mbox{arcsec}(x)$ is $\left[0,\frac{\pi}{2}\right) \cup \left(\frac{\pi}{2}, \pi\right]$.

Note

There are alternate ways to restrict the secant function to get a one-to-one function, and they lead to slightly different definitions of the inverse secant. We chose to use this restriction because it seems more “natural” than the alternatives, it is easier to evaluate on a calculator, and it is the most commonly used.

Caution

Many textbooks use the notation $\sec^{-1}(x)$ for $\mbox{arcsec}(x)$. You must be very careful to never interpret $\sec^{-1}(x)$ to mean:\[\left(\sec(x)\right)^{-1} = \frac{1}{\sec(x)} =\cos(x)\]We avoid the $\sec^{-1}(x)$ notation for this reason and suggest that you do as well.

The (restricted) secant function and the arcsecant are inverses:
\begin{align*}
\left|x\right| \geq 1 \ &\Rightarrow \ \sec\left(\mbox{arcsec}(x)\right) = x\\
0 \leq y \leq \pi \ \left(y\neq\frac{\pi}{2}\right) \ &\Rightarrow \ \mbox{arcsec}\left(\sec(y)\right) = y\end{align*}

Example $\PageIndex{5}$

Evaluate $\tan\left(\mbox{arcsec}(x)\right)$.

Solution

We want the secant of $\theta$ (the ratio of hypotenuse to adjacent) to be $x$, so we can choose the hypotenuse to be $x$ and the adjacent side to be $1$:

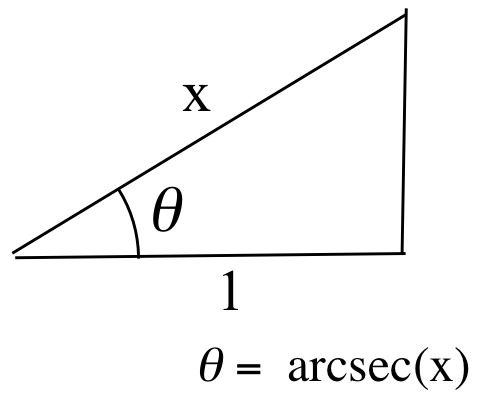
$A right triangle with hypotenuse x and base 1. Below this is the equation theta = arcsec(x).$

Then $\sec(\theta) = \frac{x}{1} = x$ and, using the Pythagorean Theorem, the length of the opposite side is $\sqrt{x^2 - 1}$, so:\[\tan\left(\mbox{arcsec}( x )\right) = \frac{\mbox{opposite}}{\mbox{adjacent}} = \frac{\sqrt{x^2 - 1}}{1} = \sqrt{x^2 - 1}\]As usual, $x$ and $1$ are the simplest — but not the only — choices.

Practice $\PageIndex{6}$

Evaluate $\sin\left(\mbox{arcsec}(x)\right)$ and $\cot\left(\mbox{arcsec}(x)\right)$.

Answer: FIGURE With hypotenuse $x$ and adjacent side $1$, the opposite side must have length $\sqrt{x^2-1^2} = \sqrt{x^2-1}$, so:
\begin{align*}
\sin\left(\arcsec\left(x\right)\right) &= \frac{\sqrt{x^2-1}}{x}\\
\cot\left(\arcsec\left(x\right)\right) &= \frac{1}{\sqrt{x^2-1}}
\end{align*}

The Other Inverse Trigonometric Functions

The inverse tangent and inverse sine functions are by far the most commonly used of the six inverse trigonometric functions in calculus. The inverse secant function turns up less often. The other three inverse trigonometric functions ($\arccos(x)$, $\mbox{arccot}(x)$ and $\mbox{arccsc}(x)$) can be defined as the inverses of restricted versions of $\cos(x)$, $\cot(x)$ and $\csc(x)$, respectively, but these functions are almost dispensable in calculus. (The reasons for this will become apparent in the next section.)

Calculators and Inverse Trigonometric Functions

Most calculators only have keys for $\sin^{-1}(x)$, $\cos^{-1}(x)$ and $\tan^{-1}(x)$, but the following identities allow you to compute values of the other inverse trigonometric functions.

Theorem

If: $x \neq 0$ and $x$ is in the appropriate domain

then: $\mbox{arccot}(x) = \arctan\left(\frac{1}{x}\right)$, $\mbox{arcsec}(x) = \arccos\left(\frac{1}{x}\right)$ and $\mbox{arccsc}(x) = \arcsin\left(\frac{1}{x}\right)$.

Proof

If $x \neq 0$, then:\[\tan\left( \mbox{arccot}( x ) \right) = \frac{1}{\cot\left( \mbox{arccot}( x ) \right)} = \frac{1}{x}\]Applying the arctangent function to each side of this equation:\[\arctan\left( \tan\left( \mbox{arccot}( x ) \right) \right) = \arctan\left(\frac{1}{x}\right) \ \Rightarrow \ \mbox{arccot}( x ) = \arctan\left(\frac{1}{x}\right)\]Proofs of the other two identities are left to you.

Theorem

If: $x \neq 0$ and $x$ is in the appropriate domain

then: $\arcsin( x ) + \arccos( x ) = \frac{\pi}{2}$, $\arctan( x ) + \mbox{arccot}( x ) = \frac{\pi}{2}$ and $\mbox{arcsec}( x ) + \mbox{arccsc}( x ) = \frac{\pi}{2}$.

Proof

If $\alpha$ and $\beta$ are complementary angles in a right triangle, so that $\alpha + \beta = \frac{\pi}{2}$, then $\sin(\alpha) = \cos(\beta)$. Let $x = \sin( \alpha ) = \cos( \beta )$ so that $\alpha = \arcsin( x )$ and $\beta = \arccos( x )$, hence:\[\alpha + \beta = \arcsin( x ) + \arccos( x ) = \frac{\pi}{2}\]This proves the first result for $0 < x < 1$. You can easily check that the result also holds for $x = 0$, $x = 1$ and $x = -1$. To check that it holds for $-1 < x < 0$, we need the the next set of identities listed below. Proofs of the other two identities above are left to you.

Theorem

If: $x$ is in the appropriate domain

then: $\arcsin( -x ) = -\arcsin(x)$, $\arccos( -x ) = \pi - \arccos(x)$, $\arctan( x ) = - \arctan(x)$, $\mbox{arcsec}( x ) = \pi-\mbox{arcsec}(x)$, $\mbox{arccsc}(-x) = -\mbox{arccsc}(x)$ and $\mbox{arccot}(-x) = -\mbox{arccot}(x)$.

Proof

If $-1 \leq x \leq 1$, let $\theta = \arcsin(-x)$ so that $\sin(\theta) = -x \Rightarrow x = -\sin(\theta) = \sin(-\theta) \Rightarrow \arcsin(x) = -\theta \Rightarrow -\arcsin(x) = \theta = \arcsin(-x)$. This proves the first identity; the others are left to you.

Some programming languages only include a single inverse trigonometric function, $\arctan(x)$, but it suffices to enable you to evaluate the other five inverse trigonometric functions:

$\displaystyle \arcsin(x) = \arctan\left(\frac{x}{\sqrt{1-x^2}}\right)$
$\displaystyle \arccos(x) = \frac{\pi}{2} - \arcsin(x) = \frac{\pi}{2} - \arctan\left(\frac{x}{\sqrt{1-x^2}}\right)$
$\displaystyle \mbox{arccot}(x) = \arctan\left(\frac{1}{x}\right)$
$\displaystyle \mbox{arcsec}(x) = \arctan\left(\sqrt{x^2-1}\right)$
$\displaystyle \mbox{arccsc}(x) = \frac{\pi}{2} - \mbox{arcsec}(x) = \frac{\pi}{2} - \arctan\left(\sqrt{x^2-1}\right)$

Problems

1. List the three smallest positive angles $\theta$ that are solutions of the equation $\sin(\theta) = 1$.
2. Evaluate $\arcsin( 1 )$ and $\mbox{arccsc}( 1 )$.
1. List the three smallest positive angles $\theta$ that are solutions of the equation $\tan( \theta ) = 1$.
2. Evaluate $\arctan( 1 )$ and $\mbox{arccot}( 1 )$.
Find all $x$ between $1$ and $7$ so that:
1. $\sin(x) = 0.3$
2. $\sin(x) = -0.4$
3. $\sin(x) = 0.5$
Find all values of $x$ between $1$ and $7$ so that:
1. $\sin(x) = 0.3$
2. $\sin(x) = -0.4$
Find all values of $x$ between $2$ and $7$ so that:
1. $\tan(x) = 3.2$
2. $\tan(x) = -0.2$
Find all values of $x$ between $1$ and $5$ so that:
1. $\tan(x) = 8$
2. $\tan(x) = -3$
In the figure below:

angle $\theta$ is
1. the arcsine of what number?
2. the arctangent of what number?
3. the arcsecant of what number?
4. the arccosine of what number?
In the figure below:

angle $\theta$ is
1. the arcsine of what number?
2. the arctangent of what number?
3. the arcsecant of what number?
4. the arccosine of what number?
For the angle $\alpha$ in the triangle below:

evaluate:
1. $\sin( \alpha )$
2. $\tan( \alpha )$
3. $\sec( \alpha )$
4. $\cos( \alpha )$
For the angle $\beta$ in the triangle Problem 9, evaluate:
1. $\sin( \beta )$
2. $\tan( \beta )$
3. $\sec( \beta )$
4. $\cos( \beta )$
For $\theta = \arcsin\left( \frac27 \right)$, find the exact values of:
1. $\tan( \theta )$
2. $\cos( \theta )$
3. $\csc( \theta )$
4. $\cot( \theta )$
For $\theta = \arctan\left( \frac92 \right)$, find the exact values of:
1. $\sin( \theta )$
2. $\cos( \theta )$
3. $\csc( \theta )$
4. $\cot( \theta )$
For $\theta = \arccos\left( \frac15 \right)$, find the exact values of:
1. $\tan( \theta )$
2. $\sin( \theta )$
3. $\csc( \theta )$
4. $\cot( \theta )$
For $\theta = \arcsin\left( \frac{a}{b} \right)$ with $0< a < b$, find the exact values of:
1. $\tan( \theta )$
2. $\cos( \theta )$
3. $\csc( \theta )$
4. $\cot( \theta )$
For $\theta = \arctan\left( \frac{a}{b} \right)$ with $0 < a < b$, find the exact values of:
1. $\tan( \theta )$
2. $\sin( \theta )$
3. $\cos( \theta )$
4. $\cot( \theta )$
For $\theta = \arctan\left( x \right)$, find the exact values of:
1. $\sin( \theta )$
2. $\cos( \theta )$
3. $\sec( \theta )$
4. $\cot( \theta )$
Find the exact values of
1. $\sin\left( \arccos( x ) \right)$
2. $\cos\left( \arcsin( x ) \right)$
3. $\sec\left( \arccos( x ) \right)$
Find the exact values of
1. $\tan\left( \arccos( x ) \right)$
2. $\cos\left( \arctan( x ) \right)$
3. $\sec\left( \arcsin( x ) \right)$
1. Does $\arcsin( 1 ) + \arcsin( 1 ) = \arcsin( 2 )$?
2. Does $\arccos( 1 ) + \arccos( 1 ) = \arccos( 2 )$?
1. What is the viewing angle for the tunnel sign in the figure below?
  $A thick black horizontal line at the bottom of the image is labeled road. Standing on the road at the far left is a green human with a brace indicating its height to be 5 ft. Near the right end of the road a purple-shaded parabolic shape is labeled 'tunnel,' with a red-shaded rectangle atop it labeled 'sign.' Braces indicate the height of the tunnel is 20 ft and the height of the tunnel is 10 ft. Dashed-black line segments extend from the head of the human to the top and bottom of the sign. A double arrow indicates the distance between the feet of the human and the base of the tunnel is 40 ft.$
2. Use arctangents to describe the viewing angle when the observer is $x$ feet from the entrance of the tunnel.
1. What is the viewing angle for the whiteboard in the figure below?
  $A thick black horizontal line is at the bottom of the image. Seated on a chair sitting on the horizontal line at the far left is a green human with a brace indicating the height of its head above the horizontal to be 4 ft. Near the right end of the horizontal line is a perpendicular vertical line segment with a thin red rectangle atop it. Braces indicate the height of the rectangle is 4 ft. and the segment below it is 3 ft. A double arrow indicates the horizontal distance between the human and the rectangle is 15 ft. Dashed-black line segments extend from the head of the human to the top and bottom of the rectangle.$
2. Use arctangents to describe the viewing angle when the student is $x$ feet from the wall.
Graph $y = \arcsin( 2x )$ and $y = \arctan( 2x )$.
Graph $y = \arcsin\left( \frac{x}{2} \right)$ and $y = \arctan\left( \frac{x}{2} \right)$.
Which curve is longer, $y = \sin(x)$ from $x = 0$ to $x = \pi$, or $y = \arcsin(x)$ from $x = -1$ to $x = 1$?

For Problems 25–28, $\displaystyle \frac{d\theta}{dt}\bigg|_{\theta=1.3} = 12$, and $\theta$ and $h$ are related by the given formula. Find $\displaystyle \frac{dh}{dt}\bigg|_{\theta=1.3}$.

$\displaystyle \sin(\theta) = \frac{h}{20}$
$\displaystyle \tan(\theta) = \frac{h}{50}$
$\displaystyle \cos(\theta) = 3h+20$
$\displaystyle 3+\tan(\theta) = 7h$

For Problems 29–32, $\displaystyle \frac{dh}{dt}\bigg|_{\theta=1.3} = 4$, and $\theta$ and $h$ are related by the given formula. Find $\displaystyle \frac{d\theta}{dt}\bigg|_{\theta=1.3}$.

$\displaystyle \sin(\theta) = \frac{h}{38}$
$\displaystyle \tan(\theta) = \frac{h}{40}$
$\displaystyle \cos(\theta) = 7h-23$
$\displaystyle \tan(\theta) = h^2$
You are observing a rocket launch from a position located 4000 feet from the launch pad:
$A right triangle has a solid-black base labeled '4000 ft,' along with a dashed-black height and hypotenuse. The angle between the base and hypotenuse is labeled 'theta = pi/3' and a red-shaded oval sits at the upper vertex. A caption reads: d theta d t = pi/12.$
When your observation angle of the rocket is $\frac{\pi}{3}$, the angle is increasing at $\frac{\pi}{12}$ feet per second. How fast is the rocket traveling?
You are observing a rocket launch from a position 3000 feet from the launch pad. NASA’s Twitter feed reports that when the rocket is 5000 feet high, its velocity is 100 feet per second.
1. What is the angle of elevation of the rocket when it is 5000 feet above the launch pad?
2. How fast is the angle of elevation increasing when the rocket is 5000 feet high?
Refer to the right triangle shown below:
1. Angle $\alpha$ is arcsine of what number?
2. Angle $\beta$ is arccosine of what number?
3. For positive numbers $A$ and $C$, evaluate $\arcsin\left( \frac{A}{C} \right) + \arccos\left( \frac{A}{C} \right)$.
Refer to the right triangle in Problem 35.
1. Angle $\alpha$ is arctangent of what number?
2. Angle $\beta$ is arccotangent of what number?
3. For positive numbers $A$ and $B$, evaluate $\arctan\left( \frac{A}{B} \right) + \mbox{arccot}\left( \frac{A}{B} \right)$.
Refer to the triangle from Problems 35–36.
1. Angle $\alpha$ is arcsecant of what number?
2. Angle $\beta$ is arccosecant of what number?
3. For positive numbers $B$ and $C$, evaluate $\mbox{arcsec}\left( \frac{C}{B} \right) + \mbox{arccsc}\left( \frac{C}{B} \right)$.
Describe the pattern apparent in your results from the previous three problems.
Refer to the right triangle shown below:
1. Angle $\theta$ is arctangent of what number?
2. Angle $\theta$ is arccotangent of what number?
Refer to the right triangle from the previous Problem.
1. Angle $\theta$ is arcsine of what number?
2. Angle $\theta$ is arccosecant of what number?
Refer to the triangle from Problems 39–40.
1. Angle $\theta$ is arccosine of what number?
2. Angle $\theta$ is arcsecant of what number?
Describe the pattern apparent in your results from the previous three problems.

In Problems 43–51, use a calculator (as necessary) and appropriate identities to compute the given values.

$\mbox{arcsec}( 3 )$
$\mbox{arcsec}( -2 )$
$\mbox{arcsec}( -1 )$
$\arccos( 0.5 )$
$\arccos( -0.5 )$
$\arccos( 1 )$
$\mbox{arccot}( 1 )$
$\mbox{arccot}( 0.5 )$
$\mbox{arccot}( -3 )$
For the triangle shown below:
1. $\theta = \arctan\left(\, \underline{\quad\quad} \, \right)$
2. $\theta = \mbox{arccot}\left(\, \underline{\quad\quad} \, \right)$
3. $\mbox{arccot}\left(\, \underline{\quad\quad} \, \right) = \arctan\left(\, \underline{\quad\quad} \, \right)$
For the triangle shown below:
1. $\theta = \arcsin\left(\, \underline{\quad\quad} \, \right)$
2. $\theta = \arccos\left(\, \underline{\quad\quad} \, \right)$
3. $\arccos\left(\, \underline{\quad\quad} \, \right) = \arcsin\left(\, \underline{\quad\quad} \, \right)$
Prove that $\displaystyle \mbox{arcsec}(x) = \arccos\left(\frac{1}{x}\right)$.
Prove that $\displaystyle \mbox{arccsc}(x) = \arcsin\left(\frac{1}{x}\right)$.

Using a right triangle you can show that: \begin{align*} &\tan\left( \arcsin( x ) \right) = \frac{x}{\sqrt{1 - x^2}} \\ &\quad \Rightarrow \arcsin( x ) = \arctan\left( \frac{x}{\sqrt{1 - x^2}}\right) \end{align*} Imitate this reasoning in Problems 56–57.

Evaluate $\tan\left( \mbox{arccot}( x ) \right)$ and use the result to find a formula for $\mbox{arccot}( x )$ in terms of arctangent.
Evaluate $\tan\left(\mbox{arcsec}( x ) \right)$ and use the result to find a formula for $\mbox{arcsec}( x )$ in terms of arctangent.
Let $a = \arctan( x )$ and $b = \arctan( y )$. Use the identity:\[\tan( a + b ) = \frac{\tan(a) + \tan(b)}{1 - \tan(a)\cdot\tan(b)}\]to show that:\[\arctan( x ) + \arctan( y ) = \arctan\left(\frac{x + y}{1 - xy}\right)\]

Search

Text Color

Text Size

Margin Size

Font Type

Caution

Definition: Inverse Sine

Example \(\PageIndex{1}\)

Solution

Practice \(\PageIndex{1}\)

Example \(\PageIndex{2}\)

Solution

Practice \(\PageIndex{2}\)

Caution

Definition: Inverse Tangent

Practice \(\PageIndex{3}\)

Example \(\PageIndex{3}\)

Solution

Practice \(\PageIndex{4}\)

Example \(\PageIndex{4}\)

Solution

Practice \(\PageIndex{5}\)

Definition: Inverse Secant

Note

Caution

Example \(\PageIndex{5}\)

Solution

Practice \(\PageIndex{6}\)

Theorem

Proof

Theorem

Proof

Theorem

Proof

Inverse Sine: Solving \(k = \sin(x)\) for \(x\)

Caution

Definition: Inverse Sine

Right Triangles and Arcsine

Example \(\PageIndex{1}\)

Solution

Practice \(\PageIndex{1}\)

Example \(\PageIndex{2}\)

Solution

Practice \(\PageIndex{2}\)

Inverse Tangent: Solving \(k = \tan(x)\) for \(x\)

Caution

Definition: Inverse Tangent

Right Triangles and Arctangent

Practice \(\PageIndex{3}\)

Example \(\PageIndex{3}\)

Solution

Practice \(\PageIndex{4}\)

Example \(\PageIndex{4}\)

Solution

Practice \(\PageIndex{5}\)

Inverse Secant: Solving \(k = \sec(x)\) for \(x\)

Definition: Inverse Secant

Note

Caution

Example \(\PageIndex{5}\)

Solution

Practice \(\PageIndex{6}\)

The Other Inverse Trigonometric Functions

Calculators and Inverse Trigonometric Functions

Theorem

Proof

Theorem

Proof

Theorem

Proof

Problems