7.4: Derivatives of Inverse Trigonometric Functions

Last updated
Save as PDF

Page ID: 212066

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\dsum}{\displaystyle\sum\limits} $

$ \newcommand{\dint}{\displaystyle\int\limits} $

$ \newcommand{\dlim}{\displaystyle\lim\limits} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

The three previous sections introduced the ideas of one-to-one functions and inverse functions, then used those concepts to define arcsine, arctangent and the other inverse trigonometric functions. In this section, we obtain derivative formulas for the inverse trigonometric functions and consider an important application and some of its variations.

Derivative Formulas for Inverse Trigonometric Functions

$\displaystyle \mbox{D}\left( \arcsin(x) \right) = \frac{1}{\sqrt{1 - x^2}}$ (for $\left|x\right| < 1$)
$\displaystyle \mbox{D}\left( \arccos(x) \right) = \frac{-1}{\sqrt{1 - x^2}}$ (for $\left|x\right| < 1$)
$\displaystyle \mbox{D}\left( \arctan(x) \right) = \frac{1}{1 + x^2}$ (for all $x$)
$\displaystyle \mbox{D}\left( \mbox{arccot}(x) \right) = \frac{-1}{1 + x^2}$ (for all $x$)
$\displaystyle \mbox{D}\left( \mbox{arcsec}(x) \right) = \frac{1}{\left|x\right| \sqrt{x^2 - 1}}$ (for $\left|x\right| > 1$)
$\displaystyle \mbox{D}\left( \mbox{arccsc}(x) \right) = \frac{-1}{\left|x\right| \sqrt{x^2 - 1}}$ (for $\left|x\right| > 1$)

Proof

If $y = \arctan(x)$ then $\tan(y) = x$, so differentiating with respect to $x$ and applying the Chain Rule yields:\[\sec^2(y) \cdot \frac{dy}{dx} = 1 \ \Rightarrow \ \frac{dy}{dx} = \frac{1}{\sec^2(y)}\nonumber\]Recalling the Pythagorean identity $\displaystyle \sec^2(\theta) = 1 + \tan^2(\theta)$, we can write:\[\frac{dy}{dx} = \frac{1}{\sec^2(y)} = \frac{1}{1+\tan^2(y)} = \frac{1}{1+x^2}\nonumber\]proving the second formula listed above. To prove the first formula, put $y = \arcsin(x)$ so that $\sin(y) = x$. Implicitly differentiating with respect to $x$ yields:\[\cos(y) \cdot \frac{dy}{dx} = 1 \ \Rightarrow \ \frac{dy}{dx} = \frac{1}{\cos(y)}\nonumber\]Solving the Pythagorean identity $\displaystyle \sin^2(\theta) + \cos^2(\theta) = 1$ for $\cos(\theta)$:\[\cos^2(\theta) = 1-\sin^2(\theta) \ \Rightarrow \ \cos(\theta) = \pm\sqrt{1-\sin^2(\theta)}\nonumber\]The range of $y = \arcsin(x)$ is $\displaystyle -\frac{\pi}{2} \leq y \leq \frac{\pi}{2}$, so $\cos(y) \geq 0$ and:\[\frac{dy}{dx} = \frac{1}{\cos(y)} = \frac{1}{\sqrt{1-\sin^2(y)}} = \frac{1}{\sqrt{1-x^2}}\nonumber\]For the third formula, if $y = \mbox{arcsec}(x)$ then $\sec(y) = x$, so differentiation yields:\[\sec(y) \cdot \tan(y) \cdot \frac{dy}{dx} = 1 \ \Rightarrow \ \frac{dy}{dx} = \frac{1}{\sec(y)\cdot\tan(y)}\nonumber\]Solving the Pythagorean identity $\displaystyle \sec^2(\theta) = 1 + \tan^2(\theta)$ for $\tan(\theta)$:\[\tan^2(\theta) = \sec^2(\theta)-1 \ \Rightarrow \ \tan(\theta) = \pm\sqrt{\sec^2(\theta)-1 }\nonumber\]If $x \geq 1$ then $\displaystyle 0 \leq y < \frac{\pi}{2}$ and on this interval $\displaystyle \tan(y) \geq 0$, so:\[\frac{dy}{dx} = \frac{1}{\sec(y)\cdot\tan(y)} = \frac{1}{\sec(y)\cdot\sqrt{\sec^2(y)-1 }} = \frac{1}{x\cdot\sqrt{x^2-1 }}\nonumber\]If $x \leq -1$ then $\displaystyle \frac{\pi}{2} < y \leq \pi$ and on this interval $\displaystyle \tan(y) \leq 0$ so:\[\frac{dy}{dx} = \frac{1}{\sec(y)\cdot\tan(y)} = \frac{1}{\sec(y)\cdot\left[-\sqrt{\sec^2(y)-1 }\right]} = \frac{1}{-x\cdot\sqrt{x^2-1 }}\nonumber\]Recognizing that $x = \left|x\right|$ when $x \geq 1$ and that $-x = \left|x\right|$ when $x \leq -1$, we can combine these two cases into a single compact form:\[\frac{dy}{dx} = \frac{1}{\left|x\right|\sqrt{x^2-1 }}\nonumber\]Proofs of the the remaining three formulas are nearly identical to those given above and are left for you as Problems 24–26.

Note

Notice that:

the derivative of $\arctan(x)$ is defined for all $x$, which corresponds to the domain of $\arctan(x)$
the derivative of $\arcsin(x)$ is defined only when $1-x^2 > 0$ or, equivalently, if $\left| x \right| < 1$, corresponding to the domain of $\arcsin(x)$ (omitting endpoints)
the derivative of $\mbox{arcsec}(x)$ is defined only when $x^2 - 1 > 0$ or, equivalently, if $\left| x \right| > 1$, corresponding to the domain of $\mbox{arcsec}(x)$ (omitting endpoints)

Example $\PageIndex{1}$

Compute $\displaystyle \mbox{D}\left(\arcsin\left( e^x \right) \right)$, $\displaystyle \mbox{D}\left(\arctan\left( x - 3 \right) \right)$, $\displaystyle \mbox{D}\left(\arctan^3\left( 5x \right) \right)$ and $\mbox{D}\left(\ln\left(\arcsin(x)\right)\right)$.

Solution

Each of these functions involves a composition of an inverse trigonometric function with other functions, so we need to use the Chain Rule:
\begin{align*}
\mbox{D}\left(\arcsin\left( e^x \right) \right) &= \frac{1}{\sqrt{1-\left(e^x\right)^2}} \cdot \mbox{D}\left(e^x\right) =
\frac{e^x}{\sqrt{1-e^{2x}}} \\
\mbox{D}\left(\arctan\left(x-3\right)\right) &= \frac{1}{1+\left(x-3\right)^2} \cdot \mbox{D}\left(x-3\right) \\
&= \frac{1}{1+\left(x-3\right)^2} = \frac{1}{x^2-6x+10}\\
\mbox{D}\left(\arctan^3\left( 5x \right) \right) &= 3\arctan^2\left(5x\right) \cdot \mbox{D}\left(\arctan(5x)\right) \\
&= 3\arctan^2\left(5x\right) \cdot \frac{1}{1+\left(5x\right)^2} \cdot 5 = \frac{15\arctan^2\left(5x\right)}{1+25x^2} \\
\mbox{D}\left(\ln\left(\arcsin(x)\right)\right) &= \frac{1}{\arcsin(x)} \cdot \mbox{D}\left(\arcsin(x)\right) = \frac{1}{\arcsin(x)} \cdot \frac{1}{\sqrt{1-x^2}}
\end{align*}
You have already practiced some of these differentiation patterns in Chapter 2 (see Problems 72–83 in Section 2.4).

Practice $\PageIndex{1}$

Compute $\displaystyle \mbox{D}\left(\arcsin\left( 5x \right) \right)$, $\displaystyle \mbox{D}\left(\arctan\left( x + 2 \right) \right)$, $\displaystyle \mbox{D}\left(\mbox{arcsec}\left( 7x \right) \right)$ and $\mbox{D}\left(e^{\arctan(7x)}\right)$.

Answer: Applying the Chain Rule:
\begin{align*}
\mbox{D}\left( \arcsin(5x) \right) &= \frac{1}{\sqrt{1 - (5x)^2}} \cdot 5 = \frac{5}{\sqrt{1 - 25x^2}}\\
\mbox{D}\left( \arctan(x+2) \right) &= \frac{1}{1 + (x+2)^2} = \frac{1}{x^2 + 4x + 5}\\
\mbox{D}\left( \mbox{arcsec}( 7x ) \right) &= \frac{1}{\left|7x\right| \cdot\sqrt{ (7x)^2 - 1}} \cdot 7 = \frac{1}{\left|x\right| \cdot\sqrt{ 49x^2 - 1}}\\
\mbox{D}\left( e^{\arctan(7x)} \right) &= e^{\arctan(7x)}\cdot \mbox{D}\left( \arctan(7x) \right) \\
&= e^{\arctan(7x)} \cdot \frac{1}{1 + (7x)^2} \cdot 7 = \frac{7 e^{\arctan(7x)}}{1 + 49x^2}
\end{align*}

A Classic Application

Mathematics is the study of patterns, and one of the pleasures of mathematics is that patterns can crop up in some unexpected places. The mathematician Johannes Müller first posed the version of the classical Museum Problem below in 1471; it is one of the oldest known maximization problems.

Museum Problem: The lower edge of a 5-foot-tall painting is 4 feet above your eye level:

$On the bottom left is the label 'eye' from which a dashed-black horiztonal line segment runs from left to right. Above its right endpoint is a vertical solid-black line segment and atop that is a blue-shaded rectangle labeled 'painting.' Braces indicate that the solid-black segment has height 4 ft. and the painting has height 5 ft. Two more dashed-black line segments extend from the eye to the top and bottom of the painting, with the angle between them labeled theta.$

At what distance should you stand from the wall so that your viewing angle of the painting is maximum?

On a typical sunny weekend, many people might rather be watching or playing a football or soccer game than visiting a museum or solving a calculus problem about a painting. But the pattern of the Museum Problem even appears in football and soccer. Because we also want to examine the Museum Problem in these other contexts, let’s solve the general version.

Example $\PageIndex{2}$

The lower edge of an $H$-foot-tall painting is $A$ feet above your eye level:

$On the bottom left is the label 'eye' from which a dashed-black horiztonal line segment runs from left to right, its length indicated by a double arrow to be x. Above its right endpoint is a vertical solid-black line segment and atop that is a blue-shaded rectangle labeled 'painting.' Braces indicate that the solid-black segment has height A and the painting has height H. Two more dashed-black line segments extend from the eye to the top and bottom of the painting, with the angle between them labeled theta. The angle between the top dashed segment and the horizontal is beta, and the angle between the middle dashed segment and the horizontal is alpha.$

At what distance $x$ should you stand from the painting so that your viewing angle is maximum?

Solution

Let $B = A + H$. Then $\displaystyle \tan(\alpha) = \frac{A}{x}$ and $\displaystyle \tan(\beta) = \frac{B}{x}$ so $\displaystyle \alpha = \arctan\left(\frac{A}{x}\right)$ and $\displaystyle \beta = \arctan\left(\frac{B}{x}\right)$. The viewing angle is thus:\[\theta = \beta - \alpha = \arctan\left(\frac{B}{x}\right)- \arctan\left(\frac{A}{x}\right)\nonumber\]We can maximize $\theta$ by calculating the derivative $\displaystyle \frac{d\theta}{dx}$ and finding where that derivative is $0$. Differentiation yields:
\begin{align*}
\frac{d\theta}{dx} &= \mbox{D}\left[\arctan\left(\frac{B}{x}\right)\right] - \mbox{D}\left[\arctan\left(\frac{A}{x}\right)\right]\\
&= \frac{1}{1+\left(\frac{B}{x}\right)^2} \cdot \left(\frac{-B}{x^2}\right) - \frac{1}{1+\left(\frac{A}{x}\right)^2} \cdot \left(\frac{-A}{x^2}\right)\\
&= \frac{-B}{x^2+B^2} + \frac{A}{x^2+A^2}
\end{align*}
Setting $\displaystyle \frac{d\theta}{dx} = 0$ and solving for $x$ yields $x = \sqrt{AB} = \sqrt{A(A + H)}$.

(We can disregard the endpoints, as you clearly do not have a maximum viewing angle with your nose pressed against the wall, or from an infinite distance far away from the wall.)

Now the original Museum Problem above becomes straightforward (as do the football and soccer variations below). With $A = 4$ and $H = 5$, the maximum viewing angle occurs when $x = \sqrt{4(4+5)} = 6$ feet. The maximum angle is therefore $\displaystyle \theta = \arctan\left( \frac96 \right) - \arctan\left( \frac46 \right) \approx 0.983 - 0.588 \approx 0.395$, or about $22.6^{\circ}$.

Practice $\PageIndex{2}$

In a football game, a kicker is attempting a field goal by kicking the football between the goal posts:

$A caption above a rectangular region reads 'college football field.' Midway down the right side of the rectangle is a thin blue rectangle with height 18.5 ft, its upper end 70.75 ft from the top-right corner of the big rectangle. A red vertical line labeled 'goal line' is 10 yds. to the left of the right side of the big rectangle. To the left of that are four evenly spaced, parallel, short, black vertical line segments 20 yards below the top of the big rectangle. Beyond the leftmost one of these is brown-shaded oval labeled 'ball spotted,' and 8 yds to the left of that is another brown-shaded oval labeled 'ball kicked.' Two dashed-black line segments extend from the 'ball kicked' point to the top and bottom of the blue rectangle, with the angle between them labeled theta.$

At what distance from the goal line should the ball be “spotted” so the kicker has the largest angle for making the field goal? The goal posts are 18.5 feet wide and located 10 yards beyond the goal line. (Assume that the ball is placed on a “hash mark” that is 20 yards from the edge of the field and is actually kicked from a point about 8 yards farther from the goal line than where the ball is spotted.)

Answer

$A = 10.75$ ft.\ and $H = 18.5$ ft.\ (see below) so $x = \sqrt{A(A+H)} = \sqrt{314.4375} \approx 17.73$ feet from the back edge of the endzone. Unfortunately, that is still more than 12 feet into the endzone. Our mathematical analysis shows that to maximize the angle for kicking a field goal, the ball should be kicked from a position 12 feet into the endzone, a touchdown!

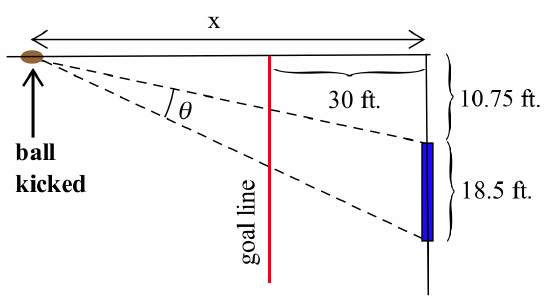
$Midway down the right side of a black rectangle is a thin blue rectangle with height 18.5 ft, its upper end 10.75 ft from the top-right corner of the big rectangle. A red vertical line labeled 'goal line' is 30 ft. to the left of the right side of the big rectangle. Further to the left and on the top of the big rectangle is a brown-shaded oval labeled 'ball kicked,' with a double arrow showing the horizontal distance to the right side of the rectangle to be x. Two dashed-black line segments extend from the 'ball kicked' point to the top and bottom of the blue rectangle, with the angle between them labeled theta.$

If the ball is placed on a hash mark just outside the endzone, then the kicking distance is 54 feet (10 yards for the depth of the endzone plus 8 yards that the ball is hiked) and the scoring angle is:\[\theta = \arctan\left(\frac{29.25}{54}\right) - \arctan\left(\frac{10.75}{54}\right) \approx 17.2^{\circ}\nonumber\]It is somewhat interesting to see investigate how the scoring angle:\[\theta = \arctan\left(\frac{29.25}{x}\right) - \arctan\left(\frac{10.75}{x}\right)\nonumber\]changes with the distance $x$ (in feet), and also to compare the scoring angle for balls placed on the hash mark with those placed in the center of the field.

Practice $\PageIndex{3}$

Kelcey is bringing a ball down the middle of a soccer field toward the 25-foot wide goal, which is defended by a goalie:

$At the right is a thin yellow rectangle labeled 'goal' with a double arrow indicating its height to be 25 ft. On the left side of the rectangle, centered vertically, are a circle with ovals at top and bottom, shaded cyan and representing an overhead vie of a person with arms outstretched. At the fat left and also centered vertically is a blue-shaded circle labeled 'ball.' Dashed-black vertical line segments extend from the ball to the endpoints of the goal and the endpoints of the person, creating three triangular regions, with the top and bottom ones labeled 'score and the middle one 'no score.' The regions above and below all of the triangles are also labeled 'no score.'$

positioned in the center of the goal. The goalie can stop a shot that is within four feet of the center of the goal. At what distance from the goal should Kelcey shoot so the scoring angle is maximum?

Answer

$A = 4$ ft.\ and $H = 8.5$ ft.\ so $x = \sqrt{A(A+H)} = \sqrt{50} \approx 7.1$ ft.:

$fig704_9.png$

From 7.1 feet, the scoring angle on one side of the goalie is:\[\theta = \arctan\left(\frac{12.5}{7.1}\right) - \arctan\left(\frac{4}{7.1}\right) \approx 31^{\circ}\nonumber\]For comparison, the table below gives values of the general scoring angle $\displaystyle \theta = \arctan\left(\frac{12.5}{x}\right) - \arctan\left(\frac{4}{x}\right)$ for some other distances $x$.

$x$	$\theta$
$5$	$29.5^\circ$
$7$	$31.0^\circ$
$10$	$29.5^\circ$
$15$	$24.9^\circ$
$20$	$20.7^\circ$
$30$	$15.0^\circ$
$40$	$11.6^\circ$

Problems

In Problems 1–21, compute the derivative.

$\displaystyle \mbox{D}\left( \arcsin( 3x ) \right)$
$\displaystyle \mbox{D}\left( \arctan( 7x ) \right)$
$\displaystyle \mbox{D}\left( \arctan( x+5 ) \right)$
$\displaystyle \mbox{D}\left( \arcsin\left( \frac{x}{2} \right) \right)$
$\displaystyle \mbox{D}\left( \arctan\left( \sqrt{x} \right) \right)$
$\displaystyle \mbox{D}\left( \mbox{arcsec}\left( x^2 \right) \right)$
$\displaystyle \mbox{D}\left( \ln\left(\arctan( x ) \right) \right)$
$\displaystyle \mbox{D}\left( x \cdot \arctan\left( x \right) \right)$
$\displaystyle \mbox{D}\left( \left(\mbox{arcsec}( x ) \right)^3 \right)$
$\displaystyle \mbox{D}\left( \arctan\left( \frac{5}{x} \right) \right)$
$\displaystyle \mbox{D}\left( \arctan\left( \ln\left(x\right) \right) \right)$
$\displaystyle \mbox{D}\left( \arcsin\left( x+2 \right) \right)$
$\displaystyle \mbox{D}\left( e^x \cdot \arctan\left( 2x \right) \right)$
$\displaystyle \mbox{D}\left( \tan(x) \cdot \arctan\left( x \right) \right)$
$\displaystyle \mbox{D}\left( \arcsin(x) + \arccos(x) \right)$
$\displaystyle \mbox{D}\left( \frac{1}{\arcsin(x)} \right)$
$\displaystyle \mbox{D}\left( \sqrt{\arcsin(x)} \right)$
$\displaystyle \mbox{D}\left( \left(1+\mbox{arcsec}( x ) \right)^3 \right)$
$\displaystyle \mbox{D}\left( \sin\left(3 + \arctan(x)\right) \right)$
$\displaystyle \mbox{D}\left( \frac{\arcsin(x)}{\arccos(x)} \right)$
$\displaystyle \mbox{D}\left( x \cdot \arctan\left( \frac{1}{x} \right) \right)$
1. Use arctangents to describe the viewing angle for the sign in the figure below:
  $A thick black horizontal line at the bottom of the image is labeled road. Standing on the road at the far left is a green human with a brace indicating its height to be 5 ft. Near the right end of the road a purple-shaded parabolic shape is labeled 'tunnel,' with a red-shaded rectangle atop it labeled 'sign.' Braces indicate the height of the tunnel is 20 ft and the height of the tunnel is 10 ft. Dashed-black line segments extend from the head of the human to the top and bottom of the sign. A double arrow indicates the distance between the feet of the human and the base of the tunnel is 40 ft.$
  when the observer is $x$ feet from the tunnel entrance.
2. At what distance $x$ is the angle maximized?
1. Use arctangents to describe the viewing angle for the whiteboard in figure below:
  $A thick black horizontal line is at the bottom of the image. Seated on a chair sitting on the horizontal line at the far left is a green human with a brace indicating the height of its head above the horizontal to be 4 ft. Near the right end of the horizontal line is a perpendicular vertical line segment with a thin red rectangle atop it. Braces indicate the height of the rectangle is 4 ft. and the segment below it is 3 ft. A double arrow indicates the horizontal distance between the human and the rectangle is 15 ft. Dashed-black line segments extend from the head of the human to the top and bottom of the rectangle.$
  when the student is $x$ feet from the front wall.
2. At what distance $x$ is the angle maximized?
Mimic the first part of the proof at the beginning of this section to show that (for all $x$):\[\mbox{D}\left( \mbox{arccot}(x) \right) = \frac{-1}{1 + x^2}\nonumber\]
Mimic the second part of the proof at the beginning of this section to show that (for $\left|x\right|<1$):\[\mbox{D}\left( \arccos(x) \right) = \frac{-1}{\sqrt{1 - x^2}}\nonumber\]
Mimic the third part of the proof at the beginning of this section to show that (for $\left|x\right|>1$):\[\mbox{D}\left( \mbox{arccsc}(x) \right) = \frac{-1}{\left|x\right|\cdot \sqrt{x^2-1}}\nonumber\]
Revisit Problem 15 and draw a triangle to arrive at your answer without using any of the derivative patterns for inverse trigonometric functions developed in this section.

\(x\)	\(\theta\)
\(5\)	\(29.5^\circ\)
\(7\)	\(31.0^\circ\)
\(10\)	\(29.5^\circ\)
\(15\)	\(24.9^\circ\)
\(20\)	\(20.7^\circ\)
\(30\)	\(15.0^\circ\)
\(40\)	\(11.6^\circ\)

Search

Text Color

Text Size

Margin Size

Font Type

Proof

Solution

Example \(\PageIndex{2}\)

Solution

Practice \(\PageIndex{2}\)

Practice \(\PageIndex{3}\)

Derivative Formulas for Inverse Trigonometric Functions

Proof

Note

Example \(\PageIndex{1}\)

Solution

Practice \(\PageIndex{1}\)

A Classic Application

Example \(\PageIndex{2}\)

Solution

Practice \(\PageIndex{2}\)

Practice \(\PageIndex{3}\)

Problems