7.A: Answers

Section 7.1

1. \(f(x)\) and \(y = 3-x\) are one-to-one because their graphs pass the horizontal line test (HLT); \(g(x)\) is not one-to-one because \(g(1) = g(4)\); \(h\) is not because its graph fails the HLT.
3. The graph of \(f(x)\) fails the HLT; \(y = e^x-2\) is one-to-one because \(y' = e^x >0\) (see Problem 13); \(g(x)\) is one-to-one because the output values are all distinct; the graph of \(h\) passes the HLT.  
5. The relation is a function if the domain is all people with a Social Security number; ideally, it is a one-to-one function (but due to identity theft and other issues may not be so in practice).  
7. No two students received the same score.
9. At most one.
11. 1. Yes (graph passes HLT).
    2. No, \(f(0) > f(1)\).
    3. No, \(f(0) < f(0.5)\).
13. \(f'(x) = \frac{1}{x} > 0\) for all \(x > 0\). If \( 0 < a < b \) with \(f(a) = f(b)\), then Rolle’s Theorem guarantees a \(c\) with \( a < c < b \) and \( f'(c) = 0 \), which is impossible. Hence \( f(a) \neq f(b) \)for any \( a \neq b \) on \( (0,\infty) \), which proves that \(f(x)\) is one-to-one.
15. 1. Yes (each input has exactly one output).
    2. Yes (each input appears only once).
    3. cde
    4. Interchanging inputs and outputs:

       a	b	c	d	e	f
       f	e	b	a	d	c

    5. Interchanging inputs and outputs:
       
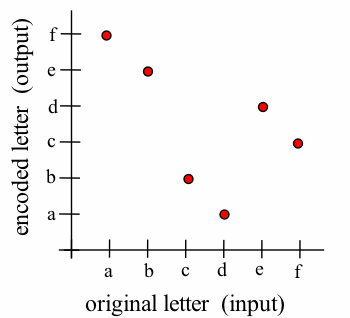
    6. They are reflections of each other.
17. 1. Yes (each output appears only once).
    2. Yes (each input appears only once).
    3. fda
    4. Interchanging inputs and outputs:

       a	b	c	d	e	f
       d	c	f	e	b	a

    5. Interchanging inputs and outputs:
       
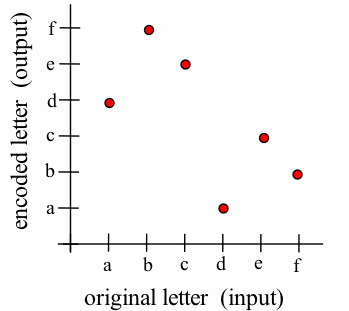
    6. It’s the same! (Function is its own inverse.)

Section 7.2

1. \(x\)	\(f(x)\)	\(f'(x)\)	\(f^{-1}(x)\)	\(\left(f^{-1}\right)'(x)\)
   \(1\)	\(3\)	\(-3\)	\(2\)	\(\frac12\)
   \(2\)	\(1\)	\(2\)	\(3\)	\(\frac13\)
   \(3\)	\(2\)	\(3\)	\(1\)	\(-\frac13\)

3. \(x\)	\(h(x)\)	\(h'(x)\)	\(h^{-1}(x)\)	\(\left(h^{-1}\right)'(x)\)
   \(1\)	\(2\)	\(2\)	\(3\)	undefined
   \(2\)	\(3\)	\(-2\)	\(1\)	\(\frac12\)
   \(3\)	\(1\)	\(0\)	\(2\)	\(-\frac12\)

5. The graphs of \(f\) and \(f^{-1}\) appear below:
   
7. \(a=b\)
9. (1) Multiply by \(4\), (2) add \(5\) and (3) divide by \(7\): \(\displaystyle f^{-1}(x) = \frac{4x+5}{7}\)
11. \(g^{-1}(x) = \frac{x-1}{2}\), hence \(g^{-1}\left(g(1)\right) = \frac{3-1}{2} = 1\) and \(g^{-1}\left(g(7)\right) = \frac{15-1}{2} = 7\).
13. \(\displaystyle w^{-1}(x) = e^{x-5}\), so \(w^{-1}\left(w(1)\right) = e^{5-5} = 1\).
15. The graph of \(f^{-1}\) goes through \((3,1)\) and \(\displaystyle \left(f^{-1}\right)'(3) = \frac{1}{f'(1)} > 0\).
17. \(\displaystyle \left(f^{-1}\right)'(x) = \frac{1}{f'\left(f^{-1}(x)\right)} > 0\), so both \(f\) and \(f^{-1}\) are increasing functions.
19. \(\displaystyle f(x) = x + 2 \Rightarrow f^{-1}(x) = x-2\) both have slope \(1\) (hence are parallel) but different \(y\)-intercepts.
21. \(f'(x) = 3 + \cos(x) \geq 2 > 0\), so \(f(x)\) is increasing, hence one-to-one.
23. \(\displaystyle x = \frac{ay+b}{cy-a} \Rightarrow cxy-ax = ay + b \Rightarrow (cx-a)y = ax+b \Rightarrow y = \frac{ax+b}{cx-a}\) so the function in (d) is its own inverse, and the functions in (a), (b) and (c) are all special cases of (d).
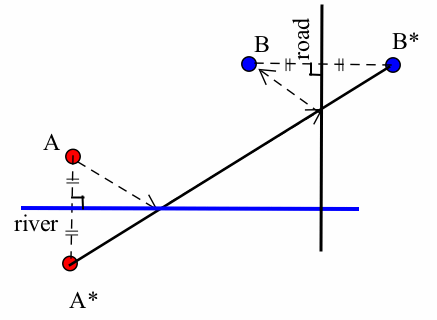
25. Fold across the river to generate point \(A^*\) (see figure below) then unfold; fold across the road to generate the point \(B^*\), then unfold; connect \(A^*\) and \(B^*\) with a line; fold the line across the river and the road to get the shortest path:
    
27. Fold across the wall:
    
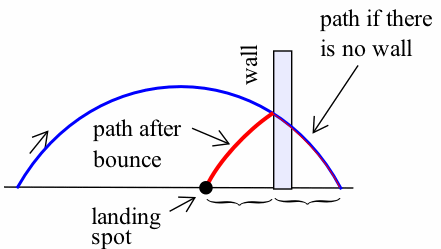
    The distance from the wall to the landing spot is the same whether the ball bounces off the wall or passes through it.

Section 7.3

1. \(\displaystyle \frac{\pi}{2}\), \(\displaystyle \frac{5\pi}{2}\), \(\displaystyle \frac{9\pi}{2}\)
3. 1. \(\arcsin(0.3)<1\) but \(\pi-\arcsin(0.3) \approx 2.837\) and \(\arcsin(0.3)+2\pi \approx 6.588\)
   2. \(\arcsin(-0.4)<1\) but \(\pi-\arcsin(-0.4) \approx 3.553\) and \(\arcsin(-0.4)+ 2\pi \approx 5.872\)
   3. \(\displaystyle \frac{5\pi}{6}\), \(\displaystyle \frac{13\pi}{6}\)
5. 1. \(\arctan(3.2) \approx 1.268\),  \(\pi + 1.268 \approx 4.410\)
   2. \(\arctan(-0.2)+\pi \approx 2.944\), \(\pi + 2.944 \approx 6.086\)
7. 1. \(\displaystyle \frac45\)
   2. \(\displaystyle \frac43\)
   3. \(\displaystyle \frac53\)
   4. \(\displaystyle \frac35\)
9. 1. \(\displaystyle \frac{5}{13}\)
   2. \(\displaystyle \frac{5}{12}\)
   3. \(\displaystyle \frac{13}{12}\)
   4. \(\displaystyle \frac{12}{13}\)
11. The triangle below should help:
    
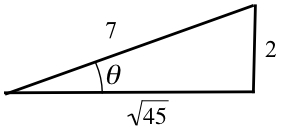
    1. \(\displaystyle \frac{2}{\sqrt{45}}\)
    2. \(\displaystyle \frac{\sqrt{45}}{7}\)
    3. \(\displaystyle \frac72\)
    4. \(\displaystyle \frac{\sqrt{45}}{2}\)
13. The triangle below should help:
    
    1. \(\displaystyle \sqrt{24}\)
    2. \(\displaystyle \frac{\sqrt{24}}{5}\)
    3. \(\displaystyle \frac{5}{\sqrt{24}}\)
    4. \(\displaystyle \frac{1}{\sqrt{24}}\)
15. The triangle below should help:
    
    1. \(\displaystyle \frac{a}{b}\)
    2. \(\displaystyle \frac{a}{\sqrt{a^2+b^2}}\)
    3. \(\displaystyle \frac{b}{\sqrt{a^2+b^2}}\)
    4. \(\displaystyle \frac{b}{a}\)
17. For \(\displaystyle 0 < \theta < \frac{\pi}{2}\), \(\cos^2(\theta)+\sin^2(\theta) = 1 \Rightarrow \sin(\theta) = \sqrt{1-\cos^2(\theta)}\) and \(\cos(\theta) = \sqrt{1-\sin^2(\theta)}\) so:
    1. \(\displaystyle \sin(\arccos(x)) = \sqrt{1-x^2}\)
    2. \(\displaystyle \cos(\arcsin(x)) = \sqrt{1-x^2}\)
    3. \(\displaystyle \sec(\arccos(x)) = \frac{1}{x}\)
19. 1. No: \(2\arcsin(1) = 2\cdot\frac{\pi}{2} = \pi\), but \(\arcsin(2)\) is not defined.
    2. No: \(2\arccos(1) = 2\cdot0 = 0\), but \(\arccos(2)\) is not defined.
21. Let \(\alpha\) represent the angle of declination from the viewer to the bottom of the whiteboard, and \(\beta\) the angle of elevation to the top:
    
    1. \(\displaystyle \alpha + \beta = \arctan\left(\frac{1}{15}\right) + \arctan\left(\frac{3}{15}\right) \approx 0.264\), or about \(15.12^{\circ}\).
    2. Replacing \(15\) with \(x\):\[\alpha + \beta = \arctan\left(\frac{1}{x}\right) + \arctan\left(\frac{3}{x}\right)\nonumber\]
23. The graphs appear below:
    
25. Differentiating implicitly, \(\displaystyle \frac{dh}{dt} = 20\cos(\theta)\cdot\frac{d\theta}{dt}\), so \(\displaystyle \frac{dh}{dt}\bigg|_{\theta=1.3} = 20\cos(1.3)\cdot 12 \approx 64.20\).
27. Differentiating implicitly, \(\displaystyle -\sin(\theta)\cdot\frac{d\theta}{dt} = 3\cdot \frac{dh}{dt}\), so \(\displaystyle \frac{dh}{dt}\bigg|_{\theta=1.3} = -\frac13\sin(1.3)\cdot 12 \approx -3.85\).
29. Differentiating implicitly, \(\displaystyle \cos(\theta)\cdot\frac{d\theta}{dt} = \frac{1}{38}\cdot \frac{dh}{dt}\), so \(\displaystyle \frac{d\theta}{dt}\bigg|_{\theta=1.3} = \frac{4}{38}\sec(1.3)\approx 0.394\).
31. Differentiating implicitly, \(\displaystyle -\sin(\theta)\cdot\frac{d\theta}{dt} = 7\cdot \frac{dh}{dt}\), so \(\displaystyle \frac{d\theta}{dt}\bigg|_{\theta=1.3} = -28\csc(1.3)\cdot 12 \approx -29.059\).
33. If \(h\) is the height of the rocket, then \(\displaystyle \tan(\theta) = \frac{h}{4000} \Rightarrow h = 4000\tan(\theta) \Rightarrow \frac{dh}{dt}  = 4000\sec^2(\theta)\cdot\frac{d\theta}{dt}\), so \(\displaystyle \frac{dh}{dt}\bigg|_{\theta=\frac{\pi}{3}} = 4000\cdot 4 \cdot\frac{\pi}{12} \approx 4189\) ft/sec.
35. 1. \(\displaystyle \alpha = \arcsin\left(\frac{A}{C}\right)\)
    2. \(\displaystyle \beta = \arccos\left(\frac{A}{C}\right)\)
    3. \(\displaystyle \arcsin\left(\frac{A}{C}\right)+\arccos\left(\frac{A}{C}\right) = \alpha + \beta = \frac{\pi}{2}\)
37. 1. \(\displaystyle \alpha = \mbox{arcsec}\left(\frac{C}{B}\right)\)
    2. \(\displaystyle \beta = \mbox{arccsc}\left(\frac{C}{B}\right)\)
    3. \(\displaystyle \mbox{arcsec}\left(\frac{C}{B}\right)+\mbox{arccsc}\left(\frac{C}{B}\right) = \alpha + \beta = \frac{\pi}{2}\)
39. 1. \(\displaystyle \frac{5}{12}\)
    2. \(\displaystyle \frac{12}{5}\)
41. 1. \(\displaystyle \frac{12}{13}\)
    2. \(\displaystyle \frac{13}{12}\)
43. \(1.231\)
45. \(\pi\)
47. \(\displaystyle \frac{2\pi}{3}\)
49. \(\displaystyle \frac{\pi}{4}\)
51. \(0.322\)
53. 1. \(\displaystyle \frac{7}{25}\)
    2. \(\displaystyle \frac{24}{25}\)
    3. \(\displaystyle \arcsin\left(\frac{7}{25}\right) = \arccos\left(\frac{24}{25}\right)\)
55. If \(x\neq 0\) then:\[\sin\left(\mbox{arccsc}\left(x\right)\right) = \frac{1}{\csc\left(\mbox{arccsc}\left(x\right)\right)} = \frac{1}{x}\nonumber\]Applying \(\arcsin\) to each side yields the result.
57. We know that \(\tan\left(\mbox{arcsec}(x)\right) = \sqrt{x^2-1}\) from Example 5, so \(\mbox{arcsec}(x) = \arctan\left(\sqrt{x^2-1}\right)\).

Section 7.4

1. \(\displaystyle \frac{1}{\sqrt{1-\left(3x\right)^2}} \cdot 3 = \frac{3}{\sqrt{1-9x^2}}\)
3. \(\displaystyle \frac{1}{1+\left(x+5\right)^2} = \frac{1}{x^2+10x+26}\)
5. \(\displaystyle \frac{1}{1+\left(\sqrt{x}\right)^2} \cdot \frac{1}{2\sqrt{x}} = \frac{1}{2\sqrt{x}\left(1+x\right)}\)
7. \(\displaystyle \frac{1}{\arctan(x)} \cdot \frac{1}{1+x^2}\)
9. \(\displaystyle 3\left(\mbox{arcsec}(x)\right)^2 \cdot \frac{1}{\left|x\right|\sqrt{x^2-1}}\)
11. \(\displaystyle \frac{1}{1+\left(\ln(x)\right)^2} \cdot \frac{1}{x}\)
13. \(\displaystyle e^x \cdot \frac{2}{1+4x^2} + \arctan(2x)\cdot e^x\)
15. \(\displaystyle \frac{1}{\sqrt{1-x^2}} - \frac{1}{\sqrt{1-x^2}} = 0\)
17. \(\displaystyle \frac{1}{2\sqrt{\arcsin(x)}} \cdot \frac{1}{\sqrt{1-x^2}}\)
19. \(\displaystyle \cos\left(3+\arctan(x)\right)\cdot \frac{1}{1+x^2}\)
21. \(\displaystyle \arctan\left(\frac{1}{x}\right) - \frac{x}{x^2+1}\)
23. 1. Use the result of Section 7.3 Problem 21:\[\theta = \arctan\left(\frac{1}{x}\right) + \arctan\left(\frac{3}{x}\right)\nonumber\]
    2. Differentiating yields:\[\frac{d\theta}{dx} = \frac{-1}{x^2+1} - \frac{3}{x^2+9} = \frac{-4\left(x^2+3\right)}{(x^2+1)(x^2+9)} < 0\nonumber\]so there are no critical points. As \(x\to\infty\), \(\theta \to 0\) (a minimum), and as \(x\to 0\), \(\theta \to \pi\): the viewer's nose touches the whiteboard!
25. With \(y = \arccos(x)\), \(\cos(y) = x\) so that:\[-\sin(y) \cdot \frac{dy}{dx} = 1 \Rightarrow \frac{dy}{dx} = \frac{-1}{\sin(y)}\nonumber\]The range of \(\arccos(y)\) is \(0 \leq y \leq \pi\), and on this interval \(\sin(y) \geq 0\), so:\[\cos^2(y) + \sin^2(y) = 1 \Rightarrow \sin(y) = \sqrt{1-\cos^2(y)} \Rightarrow \ \frac{dy}{dx} = \frac{-1}{\sqrt{1-\cos^2(y)}} = \frac{-1}{\sqrt{1-x^2}}\nonumber\]
27. For \(\displaystyle 0 < x < \frac{\pi}{2}\): \(\displaystyle \arccos(x) +\arcsin(x) = \frac{\pi}{2}\)

Section 7.5

1. \(\displaystyle 7\cdot \int \frac{1}{\sqrt{3^2-x^2}} \, dx = 7\arcsin\left(\frac{x}{3}\right)+C\)
3. \(\displaystyle 3\cdot \int_0^1 \frac{1}{5^2+x^2} \, dx = \left[\frac35\arctan\left(\frac{x}{5}\right)\right]_0^1 =\frac35\arctan\left(\frac15\right) \approx 0.1184\)
5. \(\displaystyle 9\cdot \int \frac{1}{\sqrt{7^2-x^2}} \, dx = 9\arcsin\left(\frac{x}{7}\right)+C\)
7. \(\displaystyle 3\cdot \int_6^{10} \frac{1}{x\sqrt{x^2-5^2}} \, dx = \left[\frac35\mbox{arcsec}\left(\frac{x}{5}\right)\right]_6^{10} = \frac35\left[\mbox{arcsec}\left(2\right)-\mbox{arcsec}\left(\frac{6}{5}\right)\right] \approx 0.2769\)
9. With \(u = x-1 \Rightarrow du = dx\) the integral becomes:\[\int \frac{1}{1+u^2}\, du = \arctan(u)+C = \arctan(x-1)+C\nonumber\]
11. With \(u = e^x \Rightarrow du = e^x\, dx\) the integral becomes:\[\int_{e^{-1}}^{e} \frac{1}{1+u^2}\, du = \arctan(e)-\arctan\left(e^{-1}\right) \approx 0.8658\nonumber\]
13. With \(u = \sin(\theta) \Rightarrow du = \cos(\theta)\, d\theta\) this becomes: \begin{align*}\int \frac{1}{\sqrt{3^2-u^2}}\, du &= \arcsin\left(\frac{u}{3}\right) + C \\ &= \arcsin\left(\frac{\sin(\theta)}{3}\right)+C\end{align*}
15. With \(u = 9+x^2 \Rightarrow du = 2x\, dx\) this becomes:\[\frac32\int u^{-\frac12}\, du = 3\sqrt{u}+C = 3\sqrt{9+x^2}+C\nonumber\]
17. With \(u = x^2 \Rightarrow du = 2x\, dx\) the integral becomes:\[3\int \frac{1}{3^2+u^2}\, du = \arctan\left(\frac{u}{3}\right)+C = \arctan\left(\frac{x^2}{3}\right)+C\nonumber\]
19. With \(u = 2x \Rightarrow du = 2\, dx\) the integral becomes:\[\frac12\int\frac{1}{1+u^2}\, du = \frac12\arctan(u)+C = \frac12\arctan(2x)+C\nonumber\]
21. This is an improper integral:\[\lim_{M\to\infty}\int_0^M \frac{1}{\left(\sqrt{3}\right)^2+x^2}\, dx = \lim_{M\to\infty} \left[\frac{1}{\sqrt{3}}\arctan\left(\frac{x}{\sqrt{3}}\right)\right]_0^M = \lim_{M\to\infty}\, \frac{1}{\sqrt{3}}\arctan\left(\frac{M}{\sqrt{3}}\right) = \frac{\pi}{2\sqrt{3}}\nonumber\]
23. This is an improper integral:\[\lim_{b\to\sqrt{7}^{-}}\int_0^b \frac{1}{\sqrt{\left(\sqrt{7}\right)^2-x^2}}\, dx = \lim_{b\to\sqrt{7}^{-}}\left[\arcsin\left(\frac{x}{\sqrt{7}}\right)\right]_0^b =\lim_{b\to\sqrt{7}^{-}}\, \arcsin\left(\frac{b}{\sqrt{7}}\right) = \arcsin(1) = \frac{\pi}{2}\nonumber\]
25. Separating variables:\[\int \frac{1}{y}\, dy = \int \frac{1}{\sqrt{1-x^2}}\, dx \Rightarrow \ln\left(\left|y\right|\right) = \arcsin(x)+C\nonumber\]Using \(y(0) = e\):\[\ln(e)=\arcsin(0)+ C \Rightarrow 1 = 0+C \Rightarrow C = 1\nonumber\]Solving for \(y\):\[\ln\left(\left|y\right|\right)=\arcsin(x)+1 \Rightarrow |y| = e^{\arcsin(x)+1}\nonumber\]so \(\displaystyle y = e^{\arcsin(x)+1}\) (because \(y(0)=e>0\)).
27. Separating variables:\[\int \frac{1}{y^2}\, dy = \int \frac{1}{3^2+x^2}\, dx \Rightarrow -\frac{1}{y} = \frac13 \arctan\left(\frac{x}{3}\right)+C\nonumber\]Using \(y(1)=2\):\[-\frac12 = \frac13\arctan\left(\frac13\right)+C \Rightarrow C = -\frac12-\frac13\arctan\left(\frac13\right)\nonumber\]Solving for \(y\) yields:\[y = \frac{-1}{\frac13 \arctan\left(\frac{x}{3}\right) -\frac12 -\frac13\arctan\left(\frac13\right)}\nonumber\]
29. Rewrite the integral as:\[\int \frac{4\cdot 2x}{3^2+x^2}\, dx + \int \frac{5}{3^2+x^2}\, dx\nonumber\]and integrate each term separately to get:\[4\ln\left(x^2+9\right)+\frac53\arctan\left(\frac{x}{3}\right)+C\nonumber\]
31. Rewrite the integral as:\[\frac72 \int \frac{2x}{\left(\sqrt{10}\right)^2+x^2}\, dx + 3 \int \frac{1}{\left(\sqrt{10}\right)^2+x^2}\, dx\nonumber\]and integrate each term separately to get:\[\frac72\ln\left(x^2+10\right)+\frac{3}{\sqrt{10}}\arctan\left(\frac{x}{\sqrt{10}}\right)+C\nonumber\]
33. Completing the square in the denominator, the integral becomes:\[8\int \frac{1}{1+(x+3)^2}\, dx = 8\arctan(x+3)+C\nonumber\]
35. Rewrite the integral as:\[\int\frac{2(2x+6)}{x^2+6x+10}\, dx + \int \frac{8}{1+(x+3)^2}\, dx\nonumber\]and integrate each term separately to get:\[2\ln(x^2+6x+10)+8\arctan(x+3)+C\nonumber\]
37. Use \(u = x^2+4x+5 \Rightarrow du = (2x+4)\, dx\):\[\int\frac{6(2x+4)}{x^2+4x+5}\, dx =6\int \frac{1}{u}\, du = 6\ln\left(\left|u\right|\right)+C\nonumber\]and resubstitute to get \(\displaystyle 6\ln(x^2+4x+5)+C\)
39. Rewrite the integral as:\[\int\frac{3(2x+4)}{x^2+4x+20}\, dx + \int \frac{3}{4^2+(x+2)^2}\, dx\nonumber\]and integrate each term separately to get:\[3\ln(x^2+4x+20)+\frac34\arctan\left(\frac{x+2}{4}\right)+C\nonumber\]