0.4: Combinations of Functions

Last updated
Save as PDF

Page ID: 209838

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\dsum}{\displaystyle\sum\limits} $

$ \newcommand{\dint}{\displaystyle\int\limits} $

$ \newcommand{\dlim}{\displaystyle\lim\limits} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Sometimes a physical or economic situation behaves differently depending on various circumstances. In these situations, a more complicated formula may be needed to describe the situation.

Multiline Definitions of Functions: Putting Pieces Together

Sales Tax: Some states have different rates of sales tax depending on the type of item purchased. As an example, for many years food purchased at restaurants in Seattle was taxed at a rate of 10%, while most other items were taxed at a rate of 9.5% and food purchased at grocery stores had no tax assessed. We can describe this situation by using a multiline function: a function whose defining rule consists of several pieces. Which piece of the rule we need to use will depend on what we buy. In this example, we could define the tax $T$ on an item that costs $x$ to be:

$T ( x ) = \left\{ \begin{array} { r l } { 0 } & { \text { if } x \text { if is the cost of a food at a grocery store} } \\ { 0.10x } & { \text { if } x \text { is the cost of food at a restaurant } } \\ { 0.095x } & { \text { if } x \text { is the cost of any other item } } \end{array} \right.$

To find the tax on a $2 can of stew, we would use the first piece of the rule and find that the tax is $0. To find the tax on a $30 restaurant bill, we would use the second piece of the rule and find that the tax is $3.00. The tax on a $150 textbook requires using the third rule: the tax would be $14.25.

Wind Chill Index: The rate at which a person’s body loses heat depends on the temperature of the surrounding air and on the speed of the air. You lose heat more quickly on a windy day than you do on a day with little or no wind. Scientists have experimentally determined this rate of heat loss as a function of temperature and wind speed, and the resulting function is called the Wind Chill Index, WCI. The WCI is the temperature on a still day (no wind) at which your body would lose heat at the same rate as on the windy day. For example, the WCI value for $30^{\circ}$F air moving at $15$ miles per hour is $9^{\circ}$F: your body loses heat as quickly on a $30^{\circ}$F day with a $15$ mph wind as it does on a $9^{\circ}$F day with no wind.

If $T$ is the Fahrenheit temperature of the air and $v$ is the speed of the wind in miles per hour, then the WCI can be expressed as a multiline function of the wind speed $v$ (and of the temperature $T$):\[\mbox{WCI} = \left\{\begin{array}{rl} T & \mbox{if }0\leq v \leq 4\\ 91.4 - \frac{10.45 + 6.69\sqrt{v} - 0.447v}{22} (91.5 - T) & \mbox{if }4 < v \leq 45\\ 1.60T - 55 & \mbox{if } v > 45\end{array}\right.\]The WCI value for a still day ($0 \leq v \leq 4$ mph) is just the air temperature. The WCI for wind speeds above $45$ mph are the same as the WCI for a wind speed of $45$ mph. The WCI for wind speeds between $4$ mph and $45$ mph decrease as the wind speeds increase. This WCI function depends on two variables: the temperature and the wind speed; but if the temperature is constant, then the resulting formula for WCI only depends on the wind speed. If the air temperature is $30^{\circ}$F ($T = 30$), then the formula for the Wind Chill Index is:\[\mbox{WCI}_{30} = \left\{\begin{array}{rl} 30^{\circ} & \mbox{if }0\leq v \leq 4\mbox{ mph}\\ 62.19 - 18.70\sqrt{v} +1.25v & \mbox{if }4\mbox{ mph} < v \leq 45\mbox{ mph}\\ -7^{\circ} & \mbox{if } v > 45\mbox{ mph}\end{array}\right.\] The WCI graphs for temperatures of $40^{\circ}$F, $30^{\circ}$F and $20^{\circ}$F appear below:

$Three curves showing the Wind Chill Index (WCI) as a function of wind speed (mph) for three different fixed air temperatures: 40 degrees Fahrenheit (top curve), 30 degrees Fahrenheit (middle curve), and 20 degrees Fahrenheit (bottom curve). For all temperatures, the WCI is constant (equal to the air temperature) for wind speeds between 0 and 4 mph. For wind speeds above 4 mph, the WCI decreases rapidly as wind speed increases, showing that the chill factor is greater with stronger wind. All three curves flatten out for very high wind speeds.$

Figure $\PageIndex{i}$: From UMAP Module 658, “Windchill,” by William Bosch and L.G.\ Cobb, 1984.

Practice $\PageIndex{1}$

A Hawaiian condo rents for $380 per night during the tourist season (from December 15 through April 30), and for $295 per night otherwise. Define a multiline function that describes these rates.

Answer: $C(x)$ is the cost for one night on date $x$: $C(x) = \left\{ \begin{array}{rl} { $380 } & { \text{if }x \text{ is between December 15 and April 30}}\\ { $295 } & { \text{if }x \text{ is any other date}}\end{array}\right.$

Example $\PageIndex{1}$

Define $f(x)$ by:

$f ( x ) = \left\{ \begin{array} { r l } { 2 } & { \text { if } x < 0 } \\ { 2x } & { \text { if } 0 \leq x < 2 } \\ { 1 } & { \text{ if } 2 < x } \end{array} \right.$

Evaluate $f(-3)$,$f(0)$,$f(1)$,$f(4)$ and $f(2)$. Graph $y = f(x)$ on the interval $-1 \leq x \leq 4$.

Solution

To evaluate the function at different values of $x$, we must first decide which line of the rule applies. If $x = -3 < 0$, then we need to use the first line, so $f(-3) = 2$.

When $x = 0$ or $x = 1$, we need the second line of the function definition, so $f(0) = 2(0) = 0$ and $f(1) = 2(1) = 2$.

At $x = 4$ we need the third line, so $f(4) = 1$. Finally, at $x = 2$, none of the lines apply: the second line requires $x < 2$ and the third line requires $2 < x$, so $f(2)$ is undefined. The graph of $f(x)$ appears below:

$A graph of the piecewise-defined function y = f(x). The function consists of three horizontal or linear segments. For x less than 0: A horizontal line segment at y=2, extending from the point (-1,2) (closed circle) to the point (0,2) (open circle). For x between 0 and 2 (inclusive of 0, exclusive of 2): A line segment starting at the origin (0,0) (closed circle) and extending up to the point (2,4) (open circle). For x greater than 2: A horizontal line segment at y=1, extending from the point (2,1) (open circle) to the point (4,1) (closed circle). The graph shows that f(2) is undefined because there are open circles at both (2, 4) and (2, 1).$

Note the “hole” above $x = 2$, which indicates $f(2)$ is not defined by the rule for $f$.

Practice $\PageIndex{2}$

Define $g(x)$ by: $g ( x ) = \left\{ \begin{array} { r l } { x } & { \text { if } x < -1 } \\ { 2 } & { \text{ if } -1 \leq x < 1 } \\ { -x } & { \text{ if } 1 < x } \end{array} \right.$

Graph $y = g(x)$ for $-3 \leq x \leq 6)$ and evaluate $g(-3)$, $g(-1)$, $g(0)$, $g(\frac12)$, $g(1)$, $g(\frac{\pi}{3})$, $g(2)$, $g(3)$, $g(4)$ and $g(5)$.

Answer

A graph and table appear below:
$A graph with a line segment extending from (-3,3) to an open dot at (-1,-1), then from a closed dot at (-1,2) to an open dot at (1,2), then from an open dot at (1,-1) to a closed dot at (3,-3), and finally a horizontal line segment extending right from an open dot at (4,1).$

$x$	$g(x)$	$x$	$g(x)$
$-3$	$-3$	$\frac{\pi}{3}$	$-\frac{\pi}{3}$
$-1$	$2$	$2$	$-2$
$0$	$2$	$3$	$-3$
$\frac12$	$2$	$4$	undefined
$1$	undefined	$5$	$1$

Exercise $\PageIndex{3}$

Write a multiline definition for the function whose graph appears below:

$A graph of a piecewise-defined function y=f(x). The function consists of three segments. For x less than -1: a horizontal line segment at y=1, shown as a blue line with a solid circle at (-1,1). For x between -1 and 1 (inclusive of 1, exclusive of -1): a line segment sloping down, starting at an open circle at (-1,2) and ending at a solid circle at (1,0). For x greater than 1: a horizontal line segment at y=2, shown as a blue line starting at an open circle at (1,2) and extending to the right.$

Answer: Define $f(x)$ as: $f(x) = \left\{ \begin{array}{rl} { 1 } & { \text{if }x \leq -1 } \\ { 1-x } & { \text{if }-1 < x \leq 1 } \\ { 2 } & { \text{if } 1 < x } \end{array}\right.$

We can think of a multiline function as a machine that first examines the input value to decide which line of the function rule to apply:

$A flow chart illustrating how a multiline (piecewise) function works. An Input enters a box labeled function f. Inside the box, the input goes to a decision step: Which line of the rule applies? This decision leads to one of three yellow output boxes: First line, Second line, or Last line. The output from the chosen line then exits the overall box as the Function Output = f( Input ).$

Composition of Functions: Functions of Functions

Basic functions are often combined with each other to describe more complicated situations. Here we will consider the composition of functions — functions of functions.

The composite of two functions $f$ and $g$, written $f\circ g$, is: $f\circ g(x) = f\left( g(x) \right)$

The domain of the composite function $f\circ g(x) = f\left( g(x) \right)$ consists of those $x$-values for which $g(x)$ and $f\left( g(x) \right)$ are both defined: we can evaluate the composition of two functions at a point $x$ only if each step in the composition is defined.

If we think of our functions as machines, then composition is simply a new machine consisting of an arrangement of the original machines. The composition $f\circ g$ of the function machines $f$ and $g$ shown below left is an arrangement of the machines so that the original input $x$ goes into machine $g$, the output from machine $g$ becomes the input into machine $f$, and the output from machine $f$ is our final output. The composition of the function machines $f\circ g(x) = f\left( g(x) \right)$ is only valid if $x$ is an allowable input into $g$ (that is, $x$ is in the domain of $g$) and if $g(x)$ is then an allowable input into $f$.

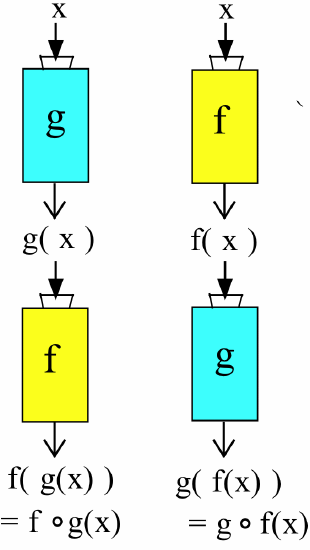
$A flow diagram illustrating function composition. On the left, input x goes into function g, then the output g(x) goes into function f, resulting in the composition f(g(x)) or f circle g (x). On the right, input x goes into function f, then the output f(x) goes into function g, resulting in the composition g(f(x)) or g circle f (x).$

The composition $g\circ f$ involves arranging the machines so the original input goes into $f$, and the output from $f$ then becomes the input for $g$ (shown above right).

Example $\PageIndex{2}$

For $f(x) = \sqrt{x - 2}$, $g(x) = x^2$ and $h(x) = \left\{ \begin{array} { r l } { 3x } & { \text{if } x < 2 } \\ { x - 1 } & { \text{ if } 2 \leq x } \end{array}\right.$ evaluate $f\circ g(3)$, $g\circ f(6)$, $f\circ h(2)$ and $h\circ g(-3)$.

Find the formulas and domains of $f\circ g(x)$ and $g\circ f(x)$.

Solution

$f\circ g(3) = f\left( g(3) \right) = f(3^2) = f(9) = \sqrt{9 - 2} = \sqrt{7} \approx 2.646$; $g\circ f(6) = g\left( f(6) \right) = g(\sqrt{6 - 2}) = g(\sqrt{4}) = g( 2 ) = 2^2 = 4$; $f\circ h(2) = f\left( h(2) \right) = f( 2 - 1 ) = f( 1 ) = \sqrt{1 - 2} = \sqrt{-1}$, which is undefined; $h\circ g(-3) = h\left( g(-3) \right) = h( 9 ) = 9 - 1 = 8$; $f\circ g(x) = f\left( g(x) \right) = f( x^2 ) = \sqrt{x^2 - 2}$, and the domain of $f\circ g$ consists of those $x$-values for which $x^2 - 2 \geq 0$, so the domain of $f\circ g$ is all $x$ such that $x \geq \sqrt{2}$ or $x \leq -\sqrt{2}$; $g\circ f(x) = g\left( f(x) \right) = g( \sqrt{x - 2} ) = \left(\sqrt{x - 2}\right)^2 = x - 2$, but this last equality is true only when $x-2 \geq 0 \Rightarrow x \geq 2$, so the domain of $g\circ f$ is all $x \geq 2$.

Practice $\PageIndex{4}$

For $f(x) = \frac{x}{x-3}$, $g(x) = \sqrt{1+x}$ and $ h(x) = \left\{ \begin{array} { r l } {2x } & { \text{ if } x \leq 1 } \\ { 5-x } & { \text{ if } 1 < x } \end{array} \right. $ evaluate $f\circ g(3)$, $f\circ g(8)$, $g\circ f(4)$, $f\circ h(1)$, $f\circ h(3)$, $f\circ h(2)$ and $h{\circ}g(-1)$.

Find formulas for $f \circ g(x)$ and $g\circ f(x)$.

Answer: $f\circ g(3) = f(2) = \frac{2}{-1} = -2$; $f\circ g(8) = f(3)$ is undefined; $g\circ f(4) = g(4) = 5$; $f\circ h(1) = f(2) = \frac{2}{-1} = -2$; $f\circ h(3) = f(2) = -2$; $f\circ h(2) = f(3)$ is undefined; $h\circ g(-1) = h(0) = 0$; $f\circ g(x) = f(\sqrt{1 + x}) = \frac{1+x }{\sqrt{1+x} - 3}$, $g\circ f(x) = g\left(\frac{x}{x-3}\right) = \sqrt{1 + \frac{x}{x-3}}$

Shifting and Stretching Graphs

Some common compositions are fairly straightforward; you should recognize the effect of these compositions on graphs of the functions.

Example $\PageIndex{3}$

The figure below shows the graph of $y = f(x)$:

$A red piecewise linear graph, y = f(x). The graph increases linearly from an endpoint below y=-1 until it reaches y=1 at x=1. It is constant at y=1 from x=1 to x=2. It then increases linearly to a peak at (3, 2). Finally, it decreases linearly, crossing the x-axis at x=4.$

Graph:

$2 + f(x)$
$3\cdot f(x)$
$f(x - 1)$

Solution

All of the new graphs appear below:

$Three graphs illustrating basic function transformations on an original red piecewise-linear function, f(x). Left graph (vertical shift): shows the function f(x) (red) and 2 + f(x) (blue), labeled "shift up by 2"; The blue graph is the red graph shifted vertically up 2 units. Middle graph (vertical stretch): shows the function f(x) (red) and 3f(x) (blue), labeled "stretch vertically by a factor of 3"; the blue graph is the red graph stretched vertically by a factor of 3. Right graph (horizontal shift): shows the original function f(x) (red dashed line) and f(x-1) (black line), labeled "shift right by 1"; the black graph is the red graph shifted horizontally 1 unit to the right.$

Adding $2$ to all of the values of $f(x)$ rigidly shifts the graph of $f(x)$ upward $2$ units.
Multiplying all of the values of $f(x)$ by $3$ leaves all of the roots (zeros) of $f$ fixed: if $x$ is a root of $f$ then $f(x) = 0 \Rightarrow 3\cdot f(x) = 3(0) = 0$ so $x$ is also a root of $3 \cdot f(x)$. If $x$ is not a root of $f$, then the graph of $3f(x)$ looks like the graph of $f(x)$ stretched vertically by a factor of \(3).
The graph of $f(x-1)$ is the graph of $f(x)$ rigidly shifted $1$ unit to the right.

We could also get these results by examining the graph of $y = f(x)$, creating a table of values for $f(x)$ and the new functions:

$x$	$f(x)$	$2 + f(x)$	$3f(x)$	$x-1$	$f(x-1)$
$-1$	$-1$	$1$	$-3$	$-2$	$f(-2)$ not defined
$0$	$0$	$2$	$0$	$-1$	$f(0-1) = -1$
$1$	$1$	$3$	$3$	$0$	$f(1-1) = 0$
$2$	$1$	$3$	$3$	$1$	$f(2-1) = 1$
$3$	$2$	$4$	$6$	$2$	$f(3-1) = 1$
$4$	$0$	$2$	$0$	$3$	$f(4-1) = 2$
$5$	$-1$	$1$	$-3$	$4$	$f(5-1) = 0$

and then graphing those new functions.

If $k$ is a positive constant, then:

the graph of $y = k + f(x)$ will be the graph of $y = f(x)$ rigidly shifted up by k units
the graph of $y = k f(x)$ will have the same roots as the graph of $f(x)$ and will be the graph of $y = f(x)$ vertically stretched by a factor of $k$
the graph of $y = f(x - k)$ will be the graph of $y = f(x)$ rigidly shifted right by $k$ units
the graph of $y = f(x + k)$ will be the graph of $y = f(x)$ rigidly shifted left by $k$ units

Practice $\PageIndex{5}$

The figure below shows the graph of $y = g(x)$:

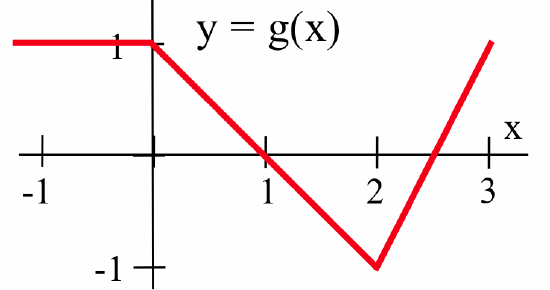
$A red piecewise linear graph, y = g(x), defined from x = -1 to x = 3. The graph is a horizontal line segment at y=1 until x=0. It then decreases linearly, crossing the x-axis at x=1, reaching a minimum at (2, -1), and increases linearly thereafter.$

Graph:

$1 + g(x)$
$2\cdot g(x)$
$g(x - 1)$
$-3\cdot g(x)$

Answer: See the figure below:
$Four side-by-side graphs illustrating basic function transformations on an original red function g(x). The original red graph is a zigzag curve that starts high, goes down, and then goes back up. The four blue graphs show the transformations: The first graph is 1 plus g(x), which is g(x) shifted up 1 unit. The second graph is 2 times g(x), which is g(x) stretched vertically by a factor of 2. The third graph is g(x-1), which is g(x) shifted 1 unit to the right. The fourth graph is -3 times g(x), which is g(x) reflected across the x-axis and stretched vertically by a factor of 3.$

Iteration of Functions

Certain applications feed the output from a function machine back into the same machine as the new input. Each time through the machine is called an iteration of the function.

Example $\PageIndex{4}$

Suppose $\displaystyle f(x) = \frac{\frac{5}{x} + x}{2}$ and we start with the input $x = 4$ and repeatedly feed the output from $f$ back into $f$. What happens?

Solution

Creating a table:

iteration	input	output
$1$	$4$	$f(4) = \frac{\frac54 + 4}{2} = 2.625000000$
$2$	$2.625000000$	$f\left( f(4) \right) = \frac{\frac{5}{2.625} + 2.625}{2} = 2.264880952$
$3$	$2.264880952$	$f\left( f\left( f(4) \right) \right) = 2.236251251$
$4$	$2.236251251$	$2.236067985$
$5$	$2.236067985$	$2.236067977$
$6$	$2.236067977$	$2.236067977$

Once we have obtained the output $2.236067977$, we will just keep getting the same output (to 9 decimal places). You might recognize this output value as an approximation of $\sqrt{5}$.

$A flow diagram illustrating function iteration. The initial input of 4 goes into the first function box (f) and outputs 2.625. This output is then fed back as the input into the second function box (f), which outputs 2.264880952. This process repeats, with the output of one function serving as the input for the next, showing the sequence converging toward a value.$

This algorithm always finds $\pm \sqrt{5}$. If we start with any positive input, the values will eventually get as close to $\sqrt{5}$ as we want. Starting with any negative value for the input will eventually get us close to $-\sqrt{5}$. We cannot start with $x = 0$, as $\frac50$ is undefined.

Practice $\PageIndex{6}$

What happens if we start with the input value $x = 1$ and iterate the function $\displaystyle f(x) = \frac{\frac{9}{x} + x}{2}$ several times? Do you recognize the resulting number? What do you think will happen to the iterates of $\displaystyle g(x) = \frac{\frac{A}{x} + x}{2}$? (Try several positive values of $A$.)

Answer

Using $\displaystyle f(x) = \frac{\frac{9}{x} + x}{2}$, $f(1) = \frac{\frac91 + 1}{2} = 5$, $f(5) = \frac{\frac95 + 5}{2} = 3.4$, $f(3.4) \approx 3.023529412$ and $f(3.023529412) \approx 3.000091554$. The next iteration gives $f(3.000091554) \approx 3.000000001$: these values are approaching $3$, the square root of $9$.

With $A = 6$, $\displaystyle f(x) = \frac{\frac{6}{x} + x}{2}$, so $f(1) = \frac{\frac61 + 1}{2} = 3.5$, $f(3.5) = \frac{\frac{6}{3.5} + 3.5}{2} = 2.607142857$, and the next iteration gives $f(2.607142857) \approx 2.45425636$. Then $f(2.45425636) \approx 2.449494372$, $f(2.449494372) \approx 2.449489743$ and $f(2.449489743) \approx 2.449489743$ (the output is the same as the input to 9 decimal places): these values are approaching $2.449489743$, an approximation of $\sqrt{6}$.

For any positive value $A$, the iterates of $\displaystyle f(x) = \frac{\frac{A}{x} +x}{2}$ (starting with any positive $x$) will approach $\sqrt{A}$.

Two Useful Functions: Absolute Value and Greatest Integer

Two functions (one of which should be familiar to you, the other perhaps not) possess useful properties that let us describe situations in which an object abruptly changes direction or jumps from one value to another value. Their graphs will have corners and breaks, respectively.

The absolute value function evaluated at a number $x$, $y = f(x) = \left|x\right|$, is the distance between the number $x$ and $0$.

Note

Some calculators and computer programming languages represent the absolute value function by $\mbox{abs}(x)$ or $\mbox{ABS}(x)$.

If $x$ is greater than or equal to $0$, then $| x |$ is simply $x - 0 = x$. If $x$ is negative, then $| x |$ is $0 - x = -x = -1\cdot x$, which is positive because: \[-1\cdot(\mbox{negative number}) = \mbox{a positive number}\]

Definition: $\left| x \right|$

$\left| x \right| = \left\{ \begin{array}{rl} {x } & {\text{if }x\geq 0 } \\ {-x } & {\text{if }x<0} \end{array}\right.$

We can also write: $\left|x\right| = \sqrt{x^2}$.

The domain of $y = f(x) = \left| x \right|$ consists of all real numbers. The range of $f(x) = \left| x \right|$ consists of all numbers larger than or equal to zero (all non-negative numbers). The graph of $y = f(x) = \left| x \right|$ has no holes or breaks, but it does have a sharp corner at $x = 0$:

$A red V-shaped graph of the absolute value function, y = |x|. The graph has its vertex at the origin (0, 0) and consists of two lines: y = -x for negative x-values and y = x for non-negative x-values.$

The absolute value will be useful for describing phenomena such as reflected light and bouncing balls that change direction abruptly or whose graphs have corners. The absolute value function has a number of properties we will use later.

Properties of $\left| x \right|$

For all real numbers $a$ and $b$:

$\left| a \right| = 0\cdot \left| a \right| = 0$ if and only if $a = 0$
$\left| ab \right| = \left| a \right| \cdot \left| b \right|$
$\left| a + b \right| \leq \left| a \right| + \left| b \right|$

This last property is widely known as the triangle inequality.

Taking the absolute value of a function has an interesting effect on the graph of the function: for any function $f(x)$, we have:

$\left| f(x) \right| = \left\{ \begin{array}{rl} { f(x) } & { \text{if } f(x)\geq 0 } \\ {-f(x) } & { \text{if } f(x)<0 } \end{array}\right.$

Example $\PageIndex{5}$

The figure below shows the graph of $f(x)$:

$A blue piecewise linear graph, y = f(x), defined from x = -1 to x = 4. The graph is a straight line decreasing from (-1, 2) to a minimum at (3, -2). It then increases linearly to (4, 0).$

Graph:

$\left| f(x) \right|$
$\left| 1 + f(x) \right|$
$1+\left| f(x) \right|$

Solution

The graphs appear below:

$Two graphs illustrating the transformation 1 + absolute value of f(x). Left graph: shows the function |f(x)| (red, always non-negative) and the transformed function 1 + |f(x)| (black), which is the red graph shifted up by 1 unit. Right graph: shows the original function f(x) (blue), the function 1 + f(x) (dashed blue), and the final transformed function |1 + f(x)| (red). The negative part of 1 + f(x) has been reflected above the x-axis to create the final graph |1 + f(x)|.$

In (b), we rigidly shift the graph of $f$ up $1$ unit before taking the absolute value. In (c), we take the absolute value before rigidly shifting the graph up $1$ unit.

Practice $\PageIndex{7}$

The figure below shows the graph of $g(x)$:

$A red piecewise linear graph, y = g(x), defined from x = -1 to x = 3. The graph increases linearly from (-1, 0) to a peak at (1, 2). It then decreases linearly, crossing the x-axis at x=2, and is constant at y = -1 for x greater than 2.$

Graph:

$\left| g(x) \right|$
$\left| g(x-1) \right|$
$g\left(\left|x\right|\right)$

Answer: The figure below shows some intermediate steps and final graphs:
$Three side-by-side graphs illustrating function transformations involving absolute value and horizontal shifting, based on an original red piecewise-linear function, g(x). Left Graph |g(x)|: shows the red graph g(x) and a blue graph |g(x)|; the parts of g(x) that were below the x-axis are reflected upward to create |g(x)|, which is always non-negative. Middle Graph |g(x-1)|: shows the red graph g(x), a dashed blue graph g(x-1) (which is g(x) shifted 1 unit to the right), and a thick black graph |g(x-1)|; the negative parts of the shifted function g(x-1) are reflected upward to form |g(x-1)|. Right Graph g(|x|): shows the red graph g(x) and a blue graph g(|x|); the graph g(|x|) uses the part of g(x) for x ≥ 0 and reflects it across the y-axis to the region where x < 0.$

The greatest integer function (or floor function) evaluated at a number $x$, $y = f(x) = \left\lfloor x \right\rfloor$, is the largest integer less than or equal to $x$.

The value of $\left\lfloor x \right\rfloor$ is always an integer and $\left\lfloor x \right\rfloor$ is always less than or equal to $x$. For example, $\left\lfloor 3.2 \right\rfloor = 3$, $\left\lfloor 3.9 \right\rfloor = 3$ and $\left\lfloor 3 \right\rfloor = 3$. If $x$ is positive, then $\left\lfloor x \right\rfloor$ truncates $x$ (drops the fractional part of $x$). If $x$ is negative, the situation is different: $\left\lfloor -4.2 \right\rfloor \neq -4$ because $-4$ is not less than or equal to $-4.2$: $\left\lfloor -4.2 \right\rfloor = -5$, $\left\lfloor -4.7 \right\rfloor = -5$ and $\left\lfloor -4 \right\rfloor = -4$.

Note

Historically, many textbooks have used the square brackets $\left[\mbox{ }\right]$ to represent the greatest integer function, while calculators and many programming languages use $\mbox{INT}(x)$ or $\mbox{floor}(x)$.

Definition: $\left\lfloor x \right\rfloor$

$\left\lfloor x \right\rfloor = \left\{ \begin{array}{rl} {x } & {\text{if } x \text{ is an integer} } \\ { \text{largest integer strictly less than } x } & {\text{if }x \text{ is not an integer} } \end{array}\right.$

The domain of $f(x) = \left\lfloor x \right\rfloor$ is all real numbers. The range of $f(x) = \left\lfloor x \right\rfloor$ is only the integers. The graph of $y = f(x) = \left\lfloor x \right\rfloor$ appears below.

$A graph of the greatest integer function, y = INT(x) or y = [x]. It is a step function composed of horizontal line segments. Each segment has a solid (closed) circle on the left, indicating the function value includes that integer, and an open circle on the right, indicating it excludes the next integer. The steps shown are at y = -1 (from x=-2 to x=-1, open circle at x=-1), y = 0 (from x=0 to x=1, open circle at x=1), y = 1 (from x=1 to x=2, open circle at x=2), and y = 2 (from x=2 to x=3, open circle at x=3).$

It has a jump break{\thinspace}---{\thinspace}a “step” — at each integer value of $x$, so $f(x) = \left\lfloor x \right\rfloor$ is called a {\bf step function}. Between any two consecutive integers, the graph is horizontal with no breaks or holes.

The greatest integer function is useful for describing phenomena that change values abruptly, such as postage rates as a function of weight. As of January 26, 2014, the cost to mail a first-class retail “flat” (such as a manila envelope) was \$0.98 for the first ounce and another $0.21 for each additional ounce.

The $\left\lfloor x \right\rfloor$ function can also be used for functions whose graphs are “square waves,” such as the on and off of a flashing light.

Example $\PageIndex{6}$

Graph $y = \left\lfloor 1+0.5\sin(x) \right\rfloor$.

Solution

One way to create this graph is to first graph $y = 1 + 0.5\sin(x)$, the thin curve in figure below:

$A graph comparing the sine wave y = 1 + 0.5sin(x) (black curve) with its greatest integer function, y = INT(1 + 0.5sin(x)) (red step function). The sine wave oscillates between y=0.5 and y=1.5. The greatest integer function is shown as horizontal line segments (steps) that only take the integer values y=0 or y=1, switching values when the sine wave crosses an integer boundary. For example, for x between -pi and 0, the sine wave is mostly below y=1, so the step function is at y=0.$

and then apply the greatest integer function to $y$ to get the thicker “square wave” pattern.

Practice $\PageIndex{8}$

Sketch the graph of $y = \left\lfloor x^2 \right\rfloor$ for $-2 \leq x \leq 2$.

Answer: The figure below shows the graph of $y = x^2$ and the (thicker) graph of $y = \left\lfloor x^2 \right\rfloor$:
$A graph comparing the parabola y=x^2 and the greatest integer function of x^2, y=INT(x^2). The parabola y=x^2 is a smooth blue U-shaped curve. The function y=INT(x^2) is shown as a series of horizontal red line segments (a step function) with solid endpoints on the left (at negative x values) and right (at positive x values), and open circles on the other side of the step, forming horizontal steps at y=0, 1, 2, 3, 4. The steps jump at integer values of x^2.$

A Really “Holey” Function

The graph of $\left\lfloor x\right\rfloor$ has a break or jump at each integer value, but how many breaks can a function have? The next function illustrates just how broken or “holey” the graph of a function can be.

Define a function $h(x)$ as: $h(x) = \left\{ \begin{array}{rl} {2} & { \text{if }x\text{ is a rational number} } \\ {1} & { \text{if }x\text{ is an irrational number} } \end{array}\right.$

Then $h( 3 ) = 2$, $h\left(\frac53\right) = 2$ and $h\left(-\frac25\right) = 2$, because $3$, $\frac53$ and $-\frac25$ are all rational numbers. Meanwhile, $h( \pi ) = 1$, $h(\sqrt{7}) = 1$ and $h(\sqrt{2}) = 1$, because $\pi$, $\sqrt{7}$ and $\sqrt{2}$ are all irrational numbers. These and some other points are plotted in the figure below:

$A graph used to illustrate a piecewise function that distinguishes between rational and irrational numbers. The graph shows a dashed red line at y=2 and a dashed blue line at y=1. Plotted points corresponding to rational x-values (like 1/2, 1, 2, 7/3, 3, 4) are on the dashed red line at y=2. Plotted points corresponding to irrational x-values (like square root of 2, pi) are on the dashed blue line at y=1. The note states: "(not to scale: each dash is just a point)."$

In order to analyze the behavior of $h(x)$ the following fact about rational and irrational numbers is useful.

Fact

Every interval contains both rational and irrational numbers.

Equivalently: If $a$ and $b$ are real numbers and $a < b$, then there is:

a rational number $R$ between $a$ and $b$ ($a < R < b$)
an irrational number $I$ between $a$ and $b$ ($a < I < b$

The above fact tells us that between any two places where $y = h(x) = 1$ (because $x$ is rational) there is a place where $y = h(x)$ is $2$, because there is an irrational number between any two distinct rational numbers. Similarly, between any two places where $y = h(x) = 2$ (because $x$ is irrational) there is a place where $y = h(x) = 1$, because there is a rational number between any two distinct irrational numbers.

The graph of $y = h(x)$ is impossible to actually draw, because every two points on the graph are separated by a hole. This is also an example of a function that your computer or calculator cannot graph, because in general it can not determine whether an input value of $x$ is irrational.

Example $\PageIndex{7}$

Sketch the graph of $g(x) = \left\{ \begin{array}{rl} {2} & { \text{if }x\text{ is a rational number} } \\ {x} & { \text{if }x\text{ is an irrational number} } \end{array}\right.$

Solution

A sketch of the graph of $y = g(x)$ appears below:

$A graph showing a constant dashed red line at y=2 and a dashed blue line y=g(x) = x+1 (where g(x) is not actually plotted with the function, only the line is shown). This graph is likely setting up a piecewise function where the output is 2 for rational x, and the output is x+1 for irrational x. The note states: "(not to scale -- each dash is just a point)."$

When $x$ is rational, the graph of $y = g(x)$ looks like the “holey” horizontal line $y = 2$. When $x$ is irrational, the graph of $y = g(x)$ looks like the “holey” line $y = x$.

Practice $\PageIndex{8}$

Sketch the graph of $h(x) = \left\{ \begin{array}{rl} { \sin(x) } & { \text{if }x\text{ is a rational number} }\\ { x } & { \text{if }x\text{ is an irrational number} } \end{array}\right.$

Answer: The figure below shows the “holey” graph of $y = x$ with a hole at each rational value of $x$ and the “holey” graph of $y = \sin(x)$ with a hole at each irrational value of $x$. Together they form the graph of $r(x)$.
$A dashed-blue line following the path of y=x, labeled "holey y =x," together with a dashed-red curve following the path of y=sin(x), labeled "holey y=sin(x)."$
(This is a very crude image, since we can’t really see the individual holes, which have zero width.)

Problems

If $T$ is the Celsius temperature of the air and $v$ is the speed of the wind in kilometers per hour, then:
$ \text{WCI} = \left\{\begin{array}{rl} {T } & { \text{if }0\leq v \leq 6.5}\\ {33 - \frac{10.45 + 5.29\sqrt{v} - 0.279v}{22} (33 - T) } & { \text{if }6.5 < v \leq 72 }\\ {1.6T - 19.8 } & { \text{if } v > 72 } \end{array}\right.$
1. Determine the Wind Chill Index for:
  1. a temperature of $0^\circ$C and a wind speed of $49$ km/hr
  2. a temperature of $11^\circ$C and a wind speed of $80$ km/hr.
2. Write a multiline function definition for the WCI if the temperature is $11^{\circ}$C.
Use the graph of $y = f(x)$ below to evaluate $f(0)$, $f(1)$, $f(2)$, $f(3)$, $f(4)$ and $f(5)$:
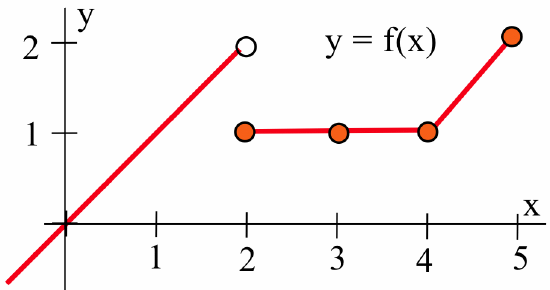
$A red piecewise linear graph, y = f(x). The function is a single line starting from the bottom left, increasing linearly, and ending at an open circle at (2, 2). The second part is a disconnected horizontal line segment at y=1, starting at a solid circle at x=2, remaining constant until x=4 (solid circle), and then increasing linearly to an open circle at (5, 2).$
Write a multiline function definition for $f$.
Use the graph of $y = g(x)$ below to evaluate $g(0)$, $g(1)$, $g(2)$, $g(3)$, $g(4)$ and $g(5)$:
$blue piecewise linear graph, y = g(x). The function has three pieces. The first piece slopes down from the top left, ending at an open circle at (1, 2). The second piece jumps down to a closed circle at (1, 1), and then increases linearly to a closed circle at (3, 3). The third piece is a horizontal line segment at y=1, starting at an open circle at (3, 1), and remaining constant to the right.$
Write a multiline function definition for $g$.

Use the values given in the table below, along with $h(x) = 2x + 1$, to determine the missing values of $f\circ g$, $g\circ f$ and $h\circ g$.

$x$	$f(x)$	$g(x)$
$-1$	$2$	$0$
$0$	$1$	$2$
$1$	$-1$	$1$
$2$	$0$	$2$

Use the graphs shown below:

and the function $h(x) = x - 2$ to determine the values of:
1. $f\left( f( 1 ) \right)$, $f\left( g( 2 ) \right)$, $f\left( g( 0 ) \right)$, $f\left( g( 1 ) \right)$
2. $g\left( f( 2 ) \right)$, $g\left( f( 3 ) \right)$, $g\left( g( 0 ) \right)$, $g\left( f( 0 ) \right)$
3. $f\left( h( 3 ) \right)$, $f\left( h( 4 ) \right)$, $h\left( g( 0 ) \right)$, $h\left( g( 1 ) \right)$
Use the graphs shown below:

and the function $h(x) = 5 - 2x$ to determine the values of:
1. $h\left( f( 0 ) \right)$, $f\left( h( 1 ) \right)$, $f\left( g( 2 ) \right)$, $f\left( f( 3 ) \right)$
2. $g\left( f( 0 ) \right)$, $g\left( f( 1 ) \right)$, $g\left( h( 2 ) \right)$, $h\left( f( 3 ) \right)$
3. $f\left( g( 0 ) \right)$, $f\left( g( 1 ) \right)$, $f\left( h( 2 ) \right)$, $h\left( g( 3 ) \right)$
Defining $h(x) = x - 2$, $f(x)$ as:
$f(x) = \left\{ \begin{array}{rl} {3} & {\text{if }x < 1}\\ {x-2} & {\text{if }1 \leq x < 3}\\ {1} & {\text{if }3 \leq x}\end{array}\right.$
and $g(x)$ as:
$g(x) = \left\{ \begin{array}{rl} {x^2-3} & {\text{if }x < 0}\\ {\left\lfloor x \right\rfloor } & { \text{if }0 \leq x } \end{array}\right.$
1. evaluate $f(x)$, $g(x)$ and $h(x)$ for $x = -1$, $0$, $1$, $2$, $3$ and $4$.
2. evaluate $f\left( g( 1 ) \right)$, $f\left( h( 1 ) \right)$, $h\left( f( 1 ) \right)$, $f\left( f( 2 ) \right)$, $g\left( g( 3.5 ) \right)$.
3. graph $f(x)$, $g(x)$ and $h(x)$ for $-5 \leq x \leq 5$.
Defining $h(x) = 3$, $f(x)$ as:
$f(x) = \left\{ \begin{array}{rl} {x+1} & {\text{if }x < 1}\\ {1 } & {\text{if }1 \leq x < 3}\\ {2-x} & {\text{if }3 \leq x}\end{array}\right.$
and $g(x)$ as:
$g(x) = \left\{ \begin{array}{rl} {\left|x+1\right|} & {\text{if }x < 0}\\ {2x} & {\text{if }0 \leq x}\end{array}\right.$
1. evaluate $f(x)$, $g(x)$ and $h(x)$ for $x = -1$, $0$, $1$, $2$, $3$ and $4$.
2. evaluate $f\left( g( 1 ) \right)$, $f\left( h( 1 ) \right)$, $h\left( f( 1 ) \right)$, $f\left( f( 2 ) \right)$, $g\left( g( 3.5 ) \right)$.
3. graph $f(x)$, $g(x)$ and $h(x)$ for $-5 \leq x \leq 5$.
You are planning to take a one-week vacation in Europe, and the tour brochure says that Monday and Tuesday will be spent in England, Wednesday in France, Thursday and Friday in Germany, and Saturday and Sunday in Italy. Let $L(d)$ be the location of the tour group on day $d$ and write a multiline function definition for $L(d)$.
A state has just adopted the following state income tax system: no tax on the first $10,000 earned, 1% of the next $10,000 earned, 2% of the next $20,000 earned, and 3% of all additional earnings. Write a multiline function definition for $T(x)$, the state income tax due on earnings of $x$ dollars.
Write a multiline function definition for the curve $y = f(x)$ shown below:
$A red piecewise graph composed of a parabola and a line segment. The first piece is the parabola y = x squared, defined from the left, ending at an open circle at (2, 4). The second piece is a line segment, starting at a disconnected open circle at (2, 1), and increasing linearly to the right.$
Define $B(x)$ to be the area of the rectangle whose lower left corner is at the origin and whose upper right corner is at the point $\left(x, f(x) \right)$ for the function $f$ shown below:
$A blue wavy curve, and a shaded red rectangular area B(x) under the curve, defined from the y-axis to a vertical dashed line at x. The rectangle's height is constant at y=1.25 (estimated average height of the area shown) and its width is x. The total area B(x) is indicated by the shaded red region bounded by the x-axis, the y-axis, the line x, and a horizontal line y=1.25. (Note: The area B(x) is more precisely the area of the rectangle formed by the input x and the constant height y=1.25).$
For example, $B(3)=6$. Evaluate $B(1)$, $B(2)$, $B(4)$ and $B(5)$.
Define $B(x)$ to be the area of the rectangle whose lower left corner is at the origin and whose upper right corner is at the point $\left(x, \frac{1}{x}\right)$.
1. Evaluate $B(1)$, $B(2)$ and $B(3)$.
2. Show that $B(x) = 1$ for all $x > 0$.
For $f(x) = \left| 9 - x \right|$ and $g(x) = \sqrt{x - 1}$:
1. evaluate $f\circ g( 1 )$, $f \circ g( 3 )$, $f\circ g( 5 )$, $f \circ g( 7 )$, $f\circ g( 0 )$.
2. evaluate $f \circ f( 2 )$, $f \circ f( 5 )$, $f\circ f( -2 )$.
3. Does $f\circ f(x) = \left|x \right|$ for all values of $x$?
The function $g(x)$ is graphed below:

Graph:
1. $g(x) - 1$
2. $g( x-1 )$
3. $\left| g(x) \right|$
4. $\left\lfloor g(x) \right\rfloor$
The function $f(x)$ is graphed below:

Graph:
1. $f(x) - 2$
2. $f( x-2 )$
3. $\left| f(x) \right|$
4. $\left\lfloor f(x) \right\rfloor$
Find $A$ and $B$ so that $f\left( g(x) \right) = g\left( f(x) \right)$ when:
1. $f(x) = 3x + 2$ and $g(x) = 2x + A$
2. $f(x) = 3x + 2$ and $g(x) = Bx - 1$
Find $C$ and $D$ so that $f\left( g(x) \right) = g\left( f(x) \right)$ when:
1. $f(x) = Cx + 3$ and $g(x) = Cx-1$
2. $f(x) = 2x + D$ and $g(x) = 3x+D$
Graph $y = f(x) = x - \left\lfloor x\right\rfloor$ for $-1 \leq x \leq 3$. This function is called the “fractional part of $x$” and its graph an example of a “sawtooth” graph.
The function $f(x) = \left\lfloor x + 0.5\right\rfloor$ rounds off $x$ to the nearest integer, while $\displaystyle g(x) = \frac{\left\lfloor 10x + 0.5\right\rfloor}{10}$ rounds off $x$ to the nearest tenth (the first decimal place). What function will round off $x$ to:
1. the nearest hundredth (two decimal places)?
2. the nearest thousandth (three decimal places)?
Modify the function in Example 6 to produce a “square wave” graph with a “long on, short off, long on, short off” pattern.
Many computer languages contain a “signum” or “sign” function defined by:
$\mbox{sgn}(x) = \left\{ \begin{array}{rl} {1} & {\text{if }x > 0}\\ {0} & {\text{if }x=0}\\ {-1} & {\text{if }x <0}\end{array}\right.$
1. Graph $\mbox{sgn}( x )$.
2. Graph $\mbox{sgn}( x - 2 )$.
3. Graph $\mbox{sgn}( x - 4 )$.
4. Graph $\mbox{sgn}( x - 2 ) \cdot \mbox{sgn}( x - 4 )$.
5. Graph $1 - \mbox{sgn}( x - 2 ) \cdot \mbox{sgn}( x - 4 )$.
6. For real numbers $a$ and $b$ with $a < b$, describe the graph of $1 - \mbox{sgn}( x - a ) \cdot \mbox{sgn}( x - b )$.
Define $g(x)$ to be the slope of the line tangent to the graph of $y = f(x)$ at $(x,y)$, with $y = f(x)$ shown here:
1. Estimate $g(1)$, $g(2)$, $g(3)$ and $g(4)$.
2. Graph $y = g(x)$ for $0 \leq x \leq 4$.
Define $h(x)$ to be the slope of the line tangent to the graph of $y = f(x)$ at $(x,y)$, with $y = f(x)$ shown here:
1. Estimate $h(1)$, $h(2)$, $h(3)$ and $h(4)$.
2. Graph $y = h(x)$ for $0 \leq x \leq 4$.
Using the cos (cosine) button on your calculator several times produces iterates of $f(x) = \cos(x)$. What number will the iterates approach if you use the cos button 20 or 30 times starting with:
1. $x = 1$?
2. $x = 2$?
3. $x = 10$?
(Be sure your calculator is in radian mode.)
Let $f(x) = 1 + \sin(x)$.
1. What happens if you start with $x = 1$ and repeatedly feed the output from $f$ back into $f$?
2. What happens if you start with $x = 2$ and examine the iterates of $f$?
(Be sure your calculator is in radian mode.)
Starting with $x = 1$, do the iterates of $f(x) = \frac{x^ 2 + 1}{2x}$ approach a number? What happens if you start with $x = 0.5$ or $x = 4$?
Let $f(x) = \frac{x}{2} + 3$.
1. What are the iterates of $f$ if you start with $x = 2$? $x = 4$? $x = 6$?
2. Find a number $c$ so that $f(c) = c$. This value of $c$ is called a fixed point of $f$.
3. Find a fixed point of $g(x) = \frac{x}{2} + A$.
Let $f(x) = \frac{x}{3} + 4$.
1. What are the iterates of $f$ if you start with $x = 2$? $x = 4$? $x = 6$?
2. Find a number $c$ so that $f(c) = c$.
3. Find a fixed point of $g(x) = \frac{x}{3} + A$.
Some iterative procedures are geometric rather than numerical. Start with an equilateral triangle with sides of length $1$, as shown at left in the figure below.
- Remove the middle third of each line segment.
- Replace the removed portion with two segments with the same length as the removed segment.
The first two iterations of this procedure are shown at center and right in the figure below:

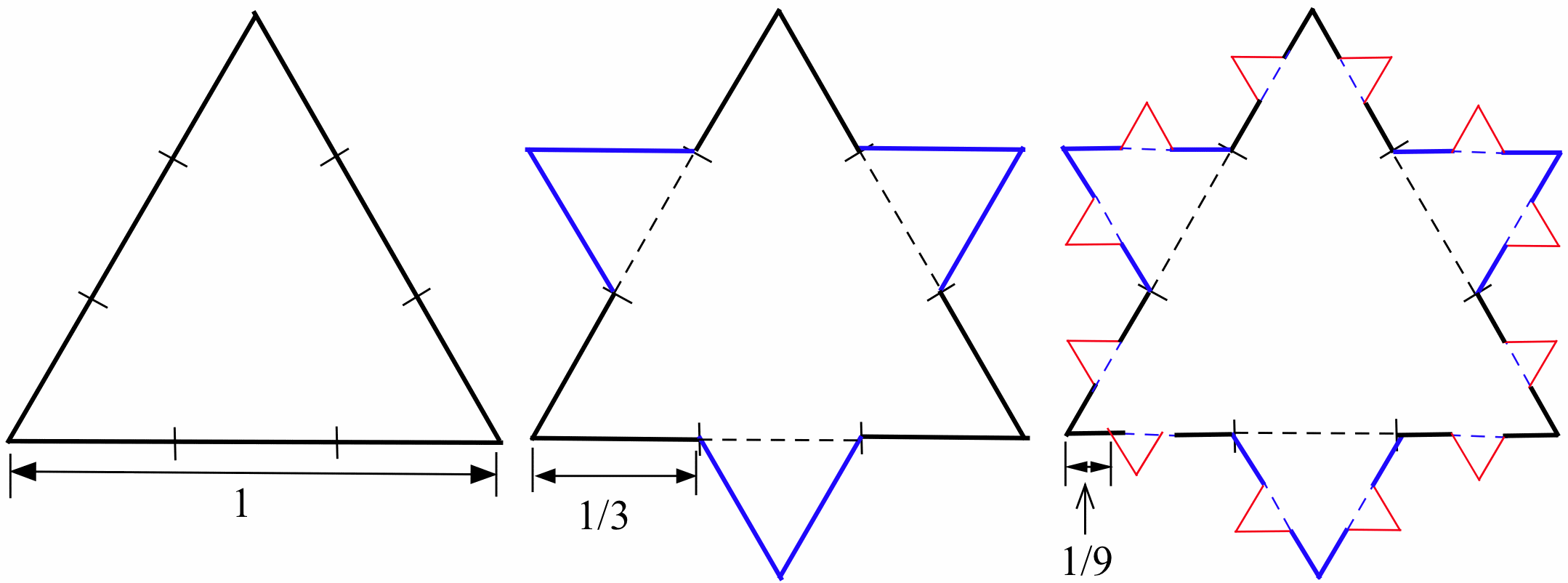
Repeat these steps several more times, each time removing the middle third of each line segment and replacing it with two new segments. What happens to the length of the shape with each iteration? (The result of iterating over and over with this procedure is called Koch’s Snowflake, named for Helga von Koch.)
Sketch the graph of: $p(x) = \left\{ \begin{array}{rl} {3-x} & {\text{if }x \text{ is a rational number}}\\ {1} & {\text{if }x \text{ is an irrational number}}\end{array}\right.$
Sketch the graph of: $q(x) = \left\{ \begin{array}{rl} {x^2} & {\text{if }x \text{ is a rational number}}\\ {x+11} & {\text{if }x \text{ is an irrational number}}\end{array}\right.$

\(x\)	\(g(x)\)	\(x\)	\(g(x)\)
\(-3\)	\(-3\)	\(\frac{\pi}{3}\)	\(-\frac{\pi}{3}\)
\(-1\)	\(2\)	\(2\)	\(-2\)
\(0\)	\(2\)	\(3\)	\(-3\)
\(\frac12\)	\(2\)	\(4\)	undefined
\(1\)	undefined	\(5\)	\(1\)

\(x\)	\(f(x)\)	\(2 + f(x)\)	\(3f(x)\)	\(x-1\)	\(f(x-1)\)
\(-1\)	\(-1\)	\(1\)	\(-3\)	\(-2\)	\(f(-2)\) not defined
\(0\)	\(0\)	\(2\)	\(0\)	\(-1\)	\(f(0-1) = -1\)
\(1\)	\(1\)	\(3\)	\(3\)	\(0\)	\(f(1-1) = 0\)
\(2\)	\(1\)	\(3\)	\(3\)	\(1\)	\(f(2-1) = 1\)
\(3\)	\(2\)	\(4\)	\(6\)	\(2\)	\(f(3-1) = 1\)
\(4\)	\(0\)	\(2\)	\(0\)	\(3\)	\(f(4-1) = 2\)
\(5\)	\(-1\)	\(1\)	\(-3\)	\(4\)	\(f(5-1) = 0\)

iteration	input	output
\(1\)	\(4\)	\(f(4) = \frac{\frac54 + 4}{2} = 2.625000000\)
\(2\)	\(2.625000000\)	\(f\left( f(4) \right) = \frac{\frac{5}{2.625} + 2.625}{2} = 2.264880952\)
\(3\)	\(2.264880952\)	\(f\left( f\left( f(4) \right) \right) = 2.236251251\)
\(4\)	\(2.236251251\)	\(2.236067985\)
\(5\)	\(2.236067985\)	\(2.236067977\)
\(6\)	\(2.236067977\)	\(2.236067977\)

\(x\)	\(f(x)\)	\(g(x)\)
\(-1\)	\(2\)	\(0\)
\(0\)	\(1\)	\(2\)
\(1\)	\(-1\)	\(1\)
\(2\)	\(0\)	\(2\)

Search

Text Color

Text Size

Margin Size

Font Type

Practice \(\PageIndex{1}\)

Example \(\PageIndex{1}\)

Solution

Practice \(\PageIndex{2}\)

Exercise \(\PageIndex{3}\)

Example \(\PageIndex{2}\)

Solution

Practice \(\PageIndex{4}\)

Example \(\PageIndex{3}\)

Solution

Practice \(\PageIndex{5}\)

Example \(\PageIndex{4}\)

Solution

Practice \(\PageIndex{6}\)

Note

Definition: \(\left| x \right|\)

Properties of \(\left| x \right|\)

Example \(\PageIndex{5}\)

Solution

Practice \(\PageIndex{7}\)

Note

Definition: \(\left\lfloor x \right\rfloor\)

Example \(\PageIndex{6}\)

Solution

Practice \(\PageIndex{8}\)

Fact

Example \(\PageIndex{7}\)

Solution

Practice \(\PageIndex{8}\)