0.A: Answers

Last updated
Save as PDF

Page ID: 210054

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\dsum}{\displaystyle\sum\limits} $

$ \newcommand{\dint}{\displaystyle\int\limits} $

$ \newcommand{\dlim}{\displaystyle\lim\limits} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Important Note about Precision of Answers: In many of the problems in this book you are required to read information from a graph and to calculate with that information. You should take reasonable care to read the graphs as accurately as you can (a small straightedge is helpful), but even skilled and careful people make slightly different readings of the same graph. That is simply one of the drawbacks of graphical information. When answers are given to graphical problems, the answers should be viewed as the best approximations we could make, and they usually include the word “approximately” or the symbol “≈” meaning “approximately equal to.” Your answers should be close to the given answers, but you should not be concerned if they differ a little. (Yes those are vague terms, but it is all we can say when dealing with graphical information.)

Section 0.1

approx.\ $1$, $0$, $-1$
1. $\displaystyle \approx \frac{70^{\circ} - 150^{\circ}}{10\mbox{ min }-0\mbox{ min }} = -8\, \frac{\circ}{\mbox{min}}$
2. $\approx 6\, \frac{\circ}{\mbox{min}}$ cooling; $5\, \frac{\circ}{\mbox{min}}$ cooling
3. $\approx 5.5\, \frac{\circ}{\mbox{min}}$ cooling; $10\, \frac{\circ}{\mbox{min}}$ cooling
4. When $t = 6$ min.
We estimate that the area is approximately (very approximately) $9$ cm$^2$.
Method 1: Measure the diameter of the can, fill it half full of water, measure the height of the water and calculate the volume. Submerge the bulb, measure the height of the water again, and calculate the new volume. The volume of the bulb is the difference of the two calculated volumes. Method 2: Fill the can with water and weigh it. Submerge the bulb (displacing a volume of water equal to the volume of the bulb), remove the bulb, and weigh the can again. By subtracting, find the weight of the displaced water and use the fact that the density of water is 1 gram per 1 cubic centimeter to determine the volume of the bulb.

Section 0.2

1. $-\frac34$
2. $\frac12$
3. $0$ \item $2$
4. undefined
1. $\frac43$
2. $-\frac95$
3. $x + 2$ (if $x \neq 2$)
4. $4 + h$ (if $h \neq 0$)
5. $a + x$ (if $a \neq x$)
1. $t = 5$: $\frac{5000}{1500} = \frac{10}{3}$; $t = 10$: $\frac{5000}{3000} = \frac53$; $t = 20$: $\frac{5000}{6000} = \frac56$
2. any $t > 0$: $\frac{5000}{300t} = \frac{50}{3t}$
3. Decreasing, since the numerator remains constant at $5000$ while the denominator increases.
The restaurant is 4 blocks south and 2 blocks east. The distance is $\sqrt{4^2 + 2^2} = \sqrt{20} \approx 4.47$ blocks.
1. $\sqrt{20^2 - 4^2} = \sqrt{384} \approx 19.6$ feet
2. $\frac{\sqrt{384}}{4} \approx 4.9$
3. $\tan( \theta ) = \frac{\sqrt{384}}{4} \approx 4.9$ so $\theta \approx 1.37$ ($\approx 78.5^{\circ}$)
1. The equation of the line through $P = (2,3)$ and $Q = (8,11)$ is $y - 3 = \frac86 (x - 2) \Rightarrow 6y - 8x = 2$. Substituting $x = 2a + 8(1-a) = 8 - 6a$ and $y = 3a + 11(1-a) = 11 - 8a$ into the equation for the line, we get: $6(11 - 8a) -8(8 - 6a) = 66 - 48a -64 + 48a = 2$ for all $a$, so the point with $x = 2a + 8(1-a)$ and $y = 3a + 11(1-a)$ is on the line through $P$ and $Q$ for any $a$. Furthermore, $2 \leq 8-6a \leq 8$ for $0 \leq a \leq 1$, so the point in question must be on the line segment $PQ$.
2. $\mbox{dist}(P,Q) = \sqrt{6^2 + 8^2} = 10$, while: \begin{align*} \mbox{dist}(P,R) &= \sqrt{(8-6a - 2)^2 + (11-8a - 3)^2}\\ &= \sqrt{(6 - 6a)^2 + (8 - 8a)^2}\\ &= \sqrt{6^2 (1-a)^2 + 8^2 (1-a)^2}\\ &= \sqrt{100(1-a)^2} = 10\cdot \left|1-a\right|\\ &= \left|1-a\right| \cdot \mbox{dist}(P,Q) \end{align*}
1. $m_1 \cdot m_2 = (1)(-1) = -1$
2. $A graphing calculator window that is wider than it is high, showing the graphs of two lines that do not appear to be perpendicular.$
3. Because $20$ units of $x$-values are physically wider on the screen than $20$ units of $y$-values.
4. Set the window so that: $\text{xmax} - \text{xmin}) \approx 1.7 (\text{ymax} - \text{ymin})$
1. $y - 5 = 3(x - 2)$ or $y = 3x - 1$
2. $y - 2 = -2(x - 3)$ or $y = 8 - 2x$
3. $y - 4 = -\frac12(x - 1)$ or $y = -\frac12 x + \frac92$
1. $y - 5 = \frac32 (x-2)$ or $y = \frac32 x + 2$
2. $y - 2 = \frac32 (x+1)$ or $y = \frac32 x + \frac72$
3. $x = 3$
Distance between the centers $= \sqrt{6^2 + 8^2} = 10$.
1. $10-2-4 = 4$
2. $10-2-7 = 1$
3. $0$ (they intersect)
4. $15-10-3 = 2$
5. $12-10-1 = 1$
Find $\mbox{dist}(P,C) = \sqrt{(x-h)^2 + (y-k)^2}$ and compare the value to $r$: \[P\mbox{ is } \left\{ \begin{array}{lll} \mbox{inside the circle } & \mbox{ if } & \mbox{dist}( P,C ) < r\\ \mbox{on the circle } & \mbox{ if } & \mbox{dist}( P,C ) = r\\ \mbox{outside the circle } & \mbox{ if } & \mbox{dist}( P,C ) > r\end{array}\right.\nonumber\]
A point $P =(x,y)$ lies on the circle if and only if its distance from $C = (h,k)$ is $r$: $\mbox{dist}( P,C ) = r$. So $P$ is on the circle if and only if: \[\sqrt{(x-h)^2 + (y-k)^2}= r\nonumber\] if and only if: \[(x-h)^2 + (y-k)^2 = r^2\nonumber\]
1. $-\frac{5}{12}$
2. undefined (vertical line)
3. $\frac{12}{5}$
4. $0$ (horizontal line)
1. $\approx 2.22$
2. $\approx 2.24$
3. (by inspection) $3$ units, which occurs at the point $(5, 3)$
1. If $B \neq 0$, we can solve for $y$: $y = -\frac{A}{B} x + \frac{C}{B}$, so the slope is $m = -\frac{A}{B}$.
2. The required slope is $\frac{B}{A}$ (the negative reciprocal of $-\frac{A}{B}$) and the $y$-intercept is $0$, so the equation is $y = \frac{B}{A} x$ or $Bx-Ay = 0$.
3. Solve the equations $Ax + By = C$ and $Bx - Ay = 0$ simultaneously to get: $ \displaystyle x = \frac{AC}{A^2 + B^2} \quad \mbox{and} \quad y = \frac{BC}{A^2+B^2}$
4. The distance from this point to the origin is: $\displaystyle \sqrt{\left(\frac{AC}{A^2 + B^2}\right)^2 + \left(\frac{BC}{A^2+B^2}\right)^2}$ \begin{align*} &= \sqrt{\frac{A^2C^2}{(A^2+B^2)^2} + \frac{B^2C^2}{(A^2+B^2)^2}}\\ & = \sqrt{\frac{(A^2+B^2)C^2}{(A^2+B^2)^2}}\\ &= \sqrt{\frac{C^2}{A^2+B^2}} = \frac{\left|C\right|}{\sqrt{A^2+B^2}} \end{align*}

Section 0.3

A: a, B: c, C: d, D:b
A: b, B: c, C: d, D: a
1. C
2. A
3. B
1. $f(1) = 4$, $g(1)$ is undefined, $H(1) = -1$
2. $Three side-by-side graphs showing different function types. The left graph is a red parabola (y = x^2) opening upward. The middle graph is a blue square root function or similar concave-down curve defined for x greater than 5. The right graph is a hyperbola or rational function with vertical asymptotes near x=2 and x=3, and a horizontal asymptote near y=0.$
3. $f( 3x ) = ( 3x )^2 + 3 = 9x^2 + 3$, $g( 3x ) = \sqrt{3x - 5}$ (for $x \geq \frac53$), $H( 3x ) = \frac{3x}{3x - 2}$
4. $f( x+h ) = (x+h)^2 + 3 = x^2 + 2xh + h^2 + 3$, $g( x+h ) = \sqrt{x + h - 5}$, $H(x + h) = \frac{x+h}{x+h - 2}$
1. $m = 2$
2. $m = 2x + 3 + h$
3. If $x = 1.3$, then $m = 5.6+h$; if $x = 1.1$, then $m = 5.2+h$; if $x = 1.002$, then $m = 5.004+h$
1. $\frac{f( a+h ) - f( a )}{h} = 2a + h - 2$ (if $h\neq 0$). If $a = 1$: $h$. If $a = 2$: $2+h$. If $a = 3$: $4 + h$. If $a = x$: $2x + h - 2$. $\frac{g( a+h ) - g( a )}{h} = \frac{1}{\sqrt{a+h} + \sqrt{a}} = \frac{\sqrt{a+h} - \sqrt{a}}{h}$. If $a = 1$: $\frac{\sqrt{1+h} - 1}{h}$. If $a = 2$: $\frac{\sqrt{2+h} - 2}{h}$. If $a = 3$: $\frac{\sqrt{3+h} - 3}{h}$. If $a = x$: $\frac{\sqrt{x+h} - x}{h}$.
1. Approx.\ $250$ miles, $375$ miles. \item Approx.\ $200$ miles/hour.
2. By flying along a circular arc about $375$ miles from the airport (or by landing at another airport).
1. FIGURE ans003_15.png
2. Largest: $x = 2$; smallest: $x = 4$.
3. Largest: at $x = 5$; smallest at $x = 3$.
The path of the slide is a straight line tangent to the graph of the path at the point of fall: FIGURE ans003_17.png}
1. $s(1) = 2$, $s(3) = \frac43$, $s(4) = \frac54$
2. $s(x) = \frac{x + 1}{x}$

Approximate values:

$x$	$f(x)$	$g(x)$
$0$	$1.0$	$1.0$
$1$	$2.0$	$1.0$
$2$	$2.0$	$-1.0$
$3$	$1.0$	$0.0$
$4$	$1.5$	$0.5$

On your own.

Section 0.4

1. $\approx - 18$, $\approx -2.2$
2. If $T = 11^{\circ}$C, $\text{WCI}_{11} =\left\{\begin{array}{rl} {11} & {\text{if } \ 0\leq v \leq 6.5}\\ {22.55 - 5.29\sqrt{v} + 0.279 v} & {\text{if } \ 6.5 < v \leq 72}\\ {-2.2} & {\text{if } \ v > 72}\end{array}\right.$
$g(0)=3$, $g(1)=1$, $g(2)=2$, $g(3)=3$, $g(4)=1$, $g(5)=1$. $g(x) = \left\{\begin{array}{rl} {3-x} & {\text{if }x<1}\\ {x} & {\text{if }1\leq x<\leq 3}\\ {1} & {\text{if }x>3}\end{array}\right.$
1. $f( f(1) ) = 1$, $f( g(2) ) = 2$,\\ $f( g(0) ) = 2$, $f( g(1) ) = 3$
2. $g( f(2) ) = 0$, $g( f(3) ) = 1$,\\ $g( g(0) ) = 0$, $g( f(0) ) = 0$
3. $f (h(3) ) = 3$, $f( h(4) ) = 2$,\\ $h( g(0) ) = 0$, $h( g(1) ) = -1$

$x$	$-1$	$0$	$1$	$2$	$3$	$4$
$f(x)$	$3$	$3$	$-1$	$0$	$1$	$1$
$g(x)$	$-2$	$0$	$1$	$2$	$3$	$4$
$h(x)$	$-3$	$-2$	$-1$	$0$	$1$	$2$

$f( g(1) ) = -1$, $f( h(1) ) = 3$, $h( f(1) ) = -3$,\\ $f( f(2) ) = 3$, $g( g(3.5) ) = 3$
$Three side-by-side graphs of different function types labeled f, g and h. Graph f is a piecewise function with a constant segment at y=1 (open circle at x=0), followed by a jump discontinuity, and a small increasing linear segment. Graph g is a piecewise function consisting of a parabola opening upward near the y-axis, followed by several disconnected constant segments (steps). Graph h is a straight line increasing linearly across the coordinate plane.$

If $L(d)$ represents location on day $d$: $L(d) = \left\{\begin{array}{ll} {\text{England } }& {\text{if } \ d = \text{Monday or Tuesday}}\\ {\text{France } }& {\text{if } \ d = \text{Wednesday}}\\ {\text{Germany } }& {\text{if } \ d = \text{Thursday or Friday}}\\ {\text{Italy } } & {\text{if } \ d = \text{Saturday}} \end{array}\right.$
Assuming the left portion is part of a parabola: $\displaystyle f(x) = \left\{\begin{array}{rl} {x^2} & {\text{if }x<2}\\ {x-1} & {\text{if }x>2}\end{array}\right.$
1. $B(1) = 1\cdot f(1) = 1\cdot \frac11 = 1$, $B(2) = 2\cdot \frac12 = 1$, $B(3) = 3 \cdot \frac13 = 1$.
2. $B(x) = x\cdot f(x) = x\cdot \frac{1}{x} = 1$ (if $x>0$)
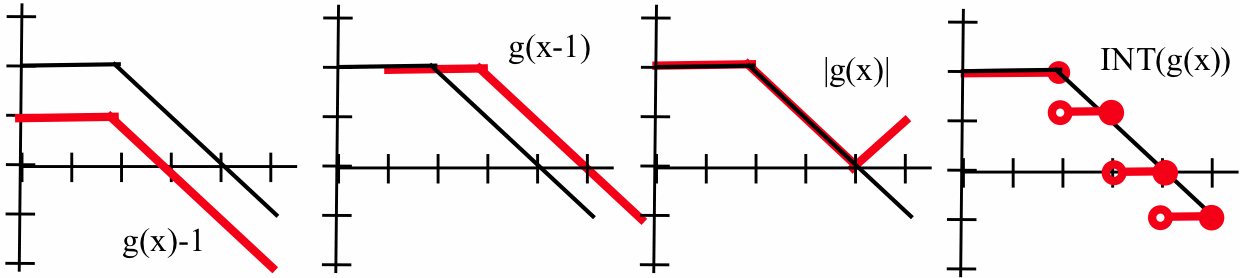
$Four side-by-side graphs illustrating transformations of a base function g(x). The original function g(x) is a black piecewise-linear function that is constant and then decreases linearly. The first graph shows g(x)-1 (red), which is g(x) shifted down by 1 unit. The second graph shows g(x-1) (red), which is g(x) shifted right by 1 unit. The third graph shows |g(x)| (red), where the negative part of g(x) is reflected above the x-axis. The fourth graph shows INT(g(x)) (red), the greatest integer function applied to g(x), resulting in a descending step function with open circles on the right side of each step.$
1. $f( g(x) ) = 6x + 2 + 3A$, $g( f(x) ) = g( 3x+2 ) = 6x + 4 + A$. If $f(g(x)) = g(f(x))$, then $A = 1$.
2. $f(g(x)) = 3Bx - 1$, $g(f(x)) = 3Bx + 2B - 1$. If $f(g(x)) = g(f(x))$, then $B = 0$.
Graph of $f(x) = x - \left\lfloor x \right\rfloor$:
$A blue graph of the fractional part function, y = x - INT(x), often called a sawtooth wave. The function consists of a series of line segments, each starting at a closed circle on the x-axis (e.g., at x=0, 1, 2) and increasing linearly with a slope of 1, ending at an open circle near y=1 just before the next integer x-value. The function has a period of 1.$
$f(x) = \left\lfloor 1.3 + 0.5\sin(x)\right\rfloor$ works. The value of $A$ in $f(x) = \left\lfloor A + 0.5\sin(x)\right\rfloor$ determines the relative lengths of the long and short parts of the pattern.
1. $g(1) = 1$, $g(2) = 1$, $g(3) = 0$, $g(4) = -1$.
2. $A smooth red curve showing a transition from y=1 to y=-1. The function is constant at y=1 for x less than 2.5, then smoothly decreases, crossing the x-axis around x=3, and becomes constant at y=-1 for x greater than 3.5. This shape resembles a smooth step function or a logistic-like curve.$
$\approx 0.739$ starting with $x = 1$, $2$, $10$ or any value
$f(1) = \frac22 = 1$. $f(0.5) = 1.25$, $f(1.25) = 1.025$, $f(1.025) \approx 1.0003049$, $f(1.0003049) \approx 1.000000046$, … $f(4) = 2.125$, $f(2.125) \approx 1.297794$, $f(1.297794) \approx 1.034166$, $f(1.034166) \approx 1.000564$, …
1. $f(2) = \frac{14}{3} \approx 4.7$, $f(\frac{14}{3}) = \frac{50}{9} \approx 5.6$, $f(\frac{50}{9}) = \frac{158}{27} \approx 5.85$, $f(\frac{158}{27}) = \frac{482}{81} \approx 5.95$ … $f(4) = \frac{16}{3} \approx 5.3$, $f(\frac{16}{3}) = \frac{52}{9} \approx 5.8$, $f(\frac{52}{9}) = \frac{160}{27} \approx 5.93$, $f(\frac{160}{27}) = \frac{484}{81} \approx 5.975$ \ldots $f(6) = 6$.
2. $c = 6$
3. Solve $c = g(c) = \frac{c}{3} + A$ to get $3c = c + 3A \Rightarrow 2c = 3A \Rightarrow c = \frac{3A}{2}$ is a fixed point of $g$.
On your own.

Section 0.5

1. $x = 2$, $4$
2. $x = -2$, $-1$, $0$, $1$, $2$, $3$, $4$, $5$
3. $x = -2$, $-1$, $1$, $3$
1. all $x$ (all real numbers)
2. $x > \sqrt[3]{-2}$
3. all $x$
1. $x = -2$, $-3$, $3$
2. no values of $x$
3. $x \geq 0$
1. If $x \neq 2$ and $x \neq -3$, then $x^2 + x - 6 \neq 0$. True.
2. If an object does not have $3$ sides, then it is not a triangle. True.
1. If your car does not get at least 24 miles per gallon, then it is not tuned properly.
2. If you cannot have dessert, then you did not eat your vegetables.
1. If you will not vote for me, then you do not love your country.
2. If not only outlaws have guns, then guns are not outlawed. (poor English) If someone legally has a gun, then guns are not illegal.
1. Both $f(x)$ and $g(x)$ are not positive.
2. $x$ is not positive. (\)x \leq 0\))
3. $8$ is not a prime number.
1. For some numbers $a$ and $b$, $\left| a+b \right| \neq \left| a \right| + \left| b \right|$.
2. Some snake is not poisonous.
3. Some dog can climb trees.
If $x$ is an integer, then $2x$ is an even integer. True. Converse: If $2x$ is an even integer, then $x$ is an integer. True. (It is not likely that these were the statements you thought of; there are lots of other examples.)
1. False. If $a = 3$, $b = 4$, then $(a + b)^2 = 7^2 = 49$, but $a^2 + b^2 = 3^2 + 4^2 = 9 + 16 = 25$.
2. False. If $a = -2$, $b = -3$, then $a > b$, but $a^2 = 4 < 9 = b^2$.
3. True.
1. True.
2. False. If $f(x) = x + 1$ and $g(x) = x + 2$, Then $f(x)\cdot g(x) = x^2 + 3x + 2$ is not a linear function.
3. True.
1. If $a$ and $b$ are prime numbers, then $a + b$ is prime. False: take $a = 3$ and $b = 5$.
2. If $a$ and $b$ are prime numbers, then $a + b$ is not prime. False: take $a = 2$ and $b = 3$.
3. If $x$ is a prime number, then $x$ is odd. False: take $x = 2$. (This is the only counterexample.)
4. If $x$ is a prime number, then $x$ is even. False: take $x = 3$ (or $5$ or $7$ or … )
1. If $x$ is a solution of $x + 5 = 9$, then $x$ is odd. False: take $x = 4$.
2. If a $3$-sided polygon has equal sides, then it is a triangle. True. (We also have non-equilateral triangles.)
3. If a person is a calculus student, then that person studies hard. False (unfortunately), but we won't mention names.
4. If $x$ is a (real number) solution of $x^2 - 5x + 6 = 0$, then $x$ is even. False: take $x = 3$.

\(x\)	\(f(x)\)	\(g(x)\)
\(0\)	\(1.0\)	\(1.0\)
\(1\)	\(2.0\)	\(1.0\)
\(2\)	\(2.0\)	\(-1.0\)
\(3\)	\(1.0\)	\(0.0\)
\(4\)	\(1.5\)	\(0.5\)

\(x\)	\(-1\)	\(0\)	\(1\)	\(2\)	\(3\)	\(4\)
\(f(x)\)	\(3\)	\(3\)	\(-1\)	\(0\)	\(1\)	\(1\)
\(g(x)\)	\(-2\)	\(0\)	\(1\)	\(2\)	\(3\)	\(4\)
\(h(x)\)	\(-3\)	\(-2\)	\(-1\)	\(0\)	\(1\)	\(2\)

Search

Text Color

Text Size

Margin Size

Font Type