2.4: The Chain Rule

The Chain Rule is the most important and most often used of the differentiation patterns. It enables us to differentiate composites of functions such as \(y = \sin( x^2 )\). It is a powerful tool for determining the derivatives of some new functions such as logarithms and inverse trigonometric functions. And it leads to important applications in a variety of fields. You will need the Chain Rule hundreds of times in this course. Practice with it now will save you time — and points — later. Fortunately, with practice, the Chain Rule is also easy to use. We already know how to differentiate the composition of some functions.

Example \(\PageIndex{1}\)

For \(f(x) = 5x - 4\) and \(g(x) = 2x + 1\), find \(f\circ g(x)\) and \(\mbox{D}( f\circ g(x) )\).

Solution

Writing \(f\circ g(x) = f( g(x) ) = 5( 2x+1) - 4 = 10x + 1\), we can compute that \(\mbox{D}( f\circ g(x) ) = \mbox{D}( 10x + 1 ) = 10\).

Practice \(\PageIndex{1}\)

For \(f(x) = 5x - 4\) and \(g(x) = x^2\), find \(f\circ g(x)\), \(\mbox{D}( f\circ g(x) )\), \(g\circ f(x)\) and \(\mbox{D}( g\circ f(x) )\).

Answer

\(f(x) = 5x - 4\) and \(g(x) = x^2 \Rightarrow f'(x) = 5\) and \(g'(x) = 2x\), so \(f\circ g(x) = f( g(x) ) = f(x^2)) = 5x^2 - 4\) and \(\mbox{D}( 5x^2 - 4 ) = 10x\) or:\[\mbox{D}( f\circ g(x) ) = f'( g(x) )\cdot g'(x) = 5\cdot 2x = 10x\]\)g\circ f(x) = g( f(x) ) = g( 5x - 4 ) = (5x - 4)^2 = 25x^2 - 40x + 16\) and \(\mbox{D}( 25x^2 - 40x + 16 ) = 50x - 40\) or:\[\mbox{D}( g\circ f(x) ) = g'( f(x) )\cdot f'(x) = 2(5x - 4)\cdot 5 = 50x - 40\]

Some compositions, however, are still very difficult to differentiate. We know the derivatives of \(g(x) = x^2\) and \(h(x) = \sin(x)\), and we know how to differentiate certain combinations of these functions, such as  \(x^2 + \sin(x)\), \(x^2\cdot \sin(x)\) and even \(\sin^2(x) = (\sin(x))^2\). But the derivative of the simple composition \(f(x) = h\circ g(x) = \sin(x^2)\) is hard — until we know the Chain Rule. (To see just how difficult, try using the definition of derivative on it.)

Example \(\PageIndex{2}\)

1. Suppose amplifier \(Y\) doubles the strength of the output signal from amplifier \(U\), and \(U\) triples the strength of the original signal \(x\). How does the final signal out of \(Y\) compare with the original signal \(x\)?
2. Suppose \(y\) changes twice as fast as \(u\), and \(u\) changes three times as fast as \(x\). How does the rate of change of \(y\) compare with the rate of change of \(x\)?

Solution

In each case we are comparing the result of a composition, and the answer to each question is \(6\), the product of the two amplifications or rates of change. In part (a), we have that:\[\frac{\mbox{signal out of }Y}{\mbox{signal }x} = \frac{\mbox{signal out of }Y}{\mbox{signal out of }U}\cdot  \frac{\mbox{signal out of }U}{\mbox{signal }x} = 2\cdot 3 = 6\nonumber\]In part (b):\[\frac{\Delta y}{\Delta x} = \frac{\Delta y}{\Delta u} \cdot \frac{\Delta u}{\Delta x} = 2\cdot 3 = 6\nonumber\]These examples are simple cases of the Chain Rule for differentiating a composition of functions.

The Chain Rule

We can express the chain rule using more than one type of notation. Each will be useful in various situations.

Chain Rule (Leibniz notation form)

If: \(y\) is a differentiable function of \(u\)

and: \(u\) is a differentiable function of \(x\)

then: \(y\) is a differentiable function of \(x\)

and: \(\displaystyle \frac{dy}{dx} = \frac{dy}{du}\cdot \frac{du}{dx}\).

Idea for a proof. If \(\Delta u \neq 0\) then:
\begin{align*}
\frac{dy}{dx} &= \lim_{\Delta x \to 0} \, \frac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0} \, \frac{\Delta y}{\Delta u} \cdot \frac{\Delta u}{\Delta x} = \left(\lim_{\Delta x \to 0} \, \frac{\Delta y}{\Delta u} \right)\left( \lim_{\Delta x \to 0} \, \frac{\Delta u}{\Delta x}\right) \\
&= \left(\lim_{\Delta u \to 0} \, \frac{\Delta y}{\Delta u} \right)\left( \lim_{\Delta x \to 0} \, \frac{\Delta u}{\Delta x}\right) = \frac{dy}{du} \cdot \frac{du}{dx}
\end{align*}
The key step here is to argue that \(\Delta x \rightarrow 0\) implies \(\Delta u \rightarrow 0\), which follows from the continuity of \(u\) as as function of \(x\). 

Although this nice short argument gets to the heart of why the Chain Rule works, it is not quite valid. If \(\frac{du}{dx} \neq 0\), then it is possible to show that \(\Delta u \neq 0\) for all “very small” values of \(\Delta x\), and the “idea for a proof” becomes a real proof. There are, however, functions for which \(\Delta u = 0\) for infinitely many small values of \(\Delta x\) (no matter how close to \(0\) we restrict \(\Delta x\)) and this creates problems with the simple argument outlined above. (A justification that holds true for {\bf all} cases is more complicated and provides no new conceptual insight. Problem 84 at the end of this section guides you through a rigorous proof of the Chain Rule.)

The symbol \(\displaystyle \frac{dy}{du}\) is a single symbol, as is \(\displaystyle \frac{du}{dx}\), so we cannot eliminate \(du\) from the product \(\displaystyle \frac{dy}{du}\frac{du}{dx}\) in the Chain Rule by “cancelling” \(du\) as we can with \(\Delta u\) in the fractions \(\displaystyle \frac{\Delta y}{\Delta u} \cdot \frac{\Delta u}{\Delta x}\). It is, however, perfectly fine to use the {\em idea} of cancelling \(du\) to help you remember the proper statement of the Chain Rule.

Example \(\PageIndex{3}\)

Write \(y = \cos(x^2 + 3)\) as \(y = \cos(u)\) with \(u = x^2 + 3\) and find \(\frac{dy}{dx}\).

Solution

\(\displaystyle y = \cos(u) \Rightarrow \frac{dy}{du} = -\sin(u)\) and \(u = x^2+3 \Rightarrow \frac{du}{dx} = 2x\). Using the Chain Rule:\[\frac{dy}{dx} = \frac{dy}{du}\cdot \frac{du}{dx} = -\sin(u) \cdot 2x = -2x\cdot\sin(x^2+3)\nonumber\]Notice that in the last step we have eliminated the intermediate variable \(u\) to express the derivative only in terms of \(x\).

Practice \(\PageIndex{2}\)

Find \(\frac{dy}{dx}\) for \(y = \sin(4x + e^x)\).

Answer

\(\displaystyle \frac{d}{dx} \left( \sin(4x + e^x) \right) = \cos(4x + e^x)\cdot \mbox{D}( 4x + e^x) = \cos(4x + e^x)\cdot ( 4 + e^x )\)

We can also state the Chain Rule in terms of composition of functions. The notation is different, but the meaning is precisely the same.

Chain Rule (composition form)

If: \(g\) is differentiable at \(x\)

and: \(f\) is differentiable at \(g(x)\)

then: the composite \(f\circ g\) is differentiable at \(x\)

and: \(( f\circ g )'(x) = \mbox{D}( f( g(x) ) ) = f'(g(x))\cdot g'(x)\).

You may find it easier to think of the result of the composition form of the Chain Rule in words: “the derivative of the outside function (evaluated at the original inside function) times the derivative of the inside function” where \(f\) is the outside function and \(g\) is the inside function.

Example \(\PageIndex{4}\)

Differentiate \(\sin( x^2)\).

Solution

We can write the function \(\sin( x^2)\) as the composition \(f\circ g\) of two simple functions: \(f(x) = \sin(x)\) and \(g(x) = x^2\): \(f\circ g (x) = f( g(x) ) = f( x^2 ) = \sin( x^2 )\). Both \(f\) and \(g\) are 
differentiable functions with derivatives \(f'(x) = \cos(x)\) and \(g'(x) = 2x\), so the Chain Rule says:
\begin{align*}\mbox{D}( \sin( x^2) ) &= ( f\circ g )'(x) = f'( g(x) )\cdot g'( x ) = \cos( g(x) ) \cdot 2x\\ &= \cos( x^2 )\cdot 2x = 2x \cos(x^2 )\end{align*}
Check that you get the same answer using the Leibniz notation. (If you tried using the definition of derivative to calculate the derivative of this function at the beginning of this section, you can really appreciate the power of the Chain Rule for differentiating compositions of functions, even simple ones like these.)

Example \(\PageIndex{5}\)

The table below gives values for \(f\), \(f'\), \(g\) and \(g'\) at various points. Use these values to determine \(( f \circ g )(x)\) and \(( f \circ g )'(x)\) at \(x = -1\) and \(x = 0\).

\(x\)	\(f(x)\)	\(g(x)\)	\(f'(x)\)	\(g'(x)\)	\((f\circ g )(x)\)	\(( f\circ g )'(x)\)
\(-1\)	\(2\)	\(3\)	\(1\)	\(0\)
\(0\)	\(-1\)	\(1\)	\(3\)	\(2\)
\(1\)	\(1\)	\(0\)	\(-1\)	\(3\)
\(2\)	\(3\)	\(-1\)	\(0\)	\(1\)
\(3\)	\(0\)	\(2\)	\(2\)	\(-1\)

Solution

\((f\circ g )(-1) = f( g(-1) ) = f( 3 ) = 0\), \(( f\circ g )(0) = f( g(0) ) = f( 1 ) = 1\), \(( f\circ g )'(-1) = f'( g(-1) )\cdot g'( -1 ) = f'( 3 )\cdot 0 = 2\cdot 0 = 0\) and \(( f\circ g )'( 0 ) = f'( g( 0 ) )\cdot g'( 0 ) = f'( 1 )\cdot 2 = (-1)(2) = -2\).

Practice \(\PageIndex{3}\)

Fill in the table in Example \(\PageIndex{5}\) for \((f\circ g )(x)\) and \((f\circ g )'(x)\) at \(x = 1\), \(2\) and \(3\).

Answer

To fill in the last column, compute:
\begin{align*}
f'( g(1) )\cdot g '(1) &= f'( 0 )\cdot 3 = (3)(3) = 9\\
f'(g(2))\cdot g'(2) &= f'( -1 )\cdot 1 = (1)(1) = 1\\
f'( g(3 )\cdot g'(3) &= f '( 2 )\cdot(-1) = (0)(-1) = 0\end{align*}

\(x\)	\(f(x)\)	\(g(x)\)	\(f'(x)\)	\(g'(x)\)	\((f\circ g )(x)\)	\(( f\circ g )'(x)\)
\(1\)	\(1\)	\(0\)	\(-1\)	\(3\)	\(-1\)	\(9\)
\(2\)	\(3\)	\(-1\)	\(0\)	\(1\)	\(2\)	\(3\)
\(3\)	\(0\)	\(2\)	\(2\)	\(-1\)	\(3\)	\(0\)

Neither form of the Chain Rule is inherently superior to the other — use the one you prefer or the one that appears most useful in a particular situation. The Chain Rule will be used hundreds of times in the rest of this book, and it is important that you master its usage. The time you spend now mastering and understanding how to use the Chain Rule will be paid back tenfold over the next several chapters.

Example \(\PageIndex{6}\)

Determine \(\displaystyle \mbox{D}\left( e^{\cos(x)} \right)\) using each form of the Chain Rule.

Solution

Using the Leibniz notation: \(y = e^u\) and \(u = \cos(x)\) so we have \(\frac{dy}{du} = e^u\) and \(\frac{du}{dx} = -\sin(x)\). Applying the Chain Rule:\[\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx} = e^u \cdot ( -\sin( x ) ) = -\sin( x )\cdot e^{\cos(x)}\nonumber\]We can also write the function \(\displaystyle e^{\cos(x)}\) as the composition of \(f(x) = e^x\) with \(g(x) = \cos(x)\), so the Chain Rule says:\[\mbox{D}( e^{\cos(x)} ) = f'( g(x) ) \cdot g '( x ) = e^{g(x)}\cdot (-\sin( x ) ) = -\sin(x)\cdot e^{\cos(x)}\nonumber\]because \(\mbox{D}( e^x ) = e^x\) and \(\mbox{D}\left(\cos(x) \right) = -\sin(x)\).

Practice \(\PageIndex{4}\)

Calculate \(\mbox{D}\left(\sin( 7x - 1 ) \right)\), \(\displaystyle \frac{d}{dx} \left(\sin( ax + b) \right)\) and \(\displaystyle \frac{d}{dt} \left( e^{3t} \right)\).

Answer

\(\mbox{D}\left( \sin(7x - 1) \right) = \cos(7x - 1)\cdot \mbox{D}( 7x - 1 ) = 7\cdot\cos(7x - 1)\)

 \(\displaystyle \frac{d}{dx} \left(\sin(ax + b)\right) = \cos(ax + b) \cdot \mbox{D}( ax + b ) = a\cdot\cos(ax + b)\)
 
 \(\displaystyle \frac{d}{dt} \left( e^{3t}\right) = e^{3t}\cdot \frac{d}{dt}\left( 3t \right) = 3\cdot e^{3t}\)

Practice \(\PageIndex{5}\)

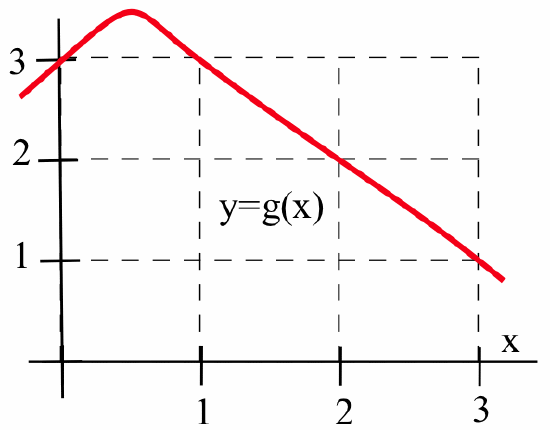
Use the graph of \(g\) given below along with the Chain Rule to estimate \(\mbox{D}\left(\sin( g(x) ) \right)\) and \(\mbox{D}\left( g(\sin(x) ) \right)\) at \(x = \pi\).

Answer

\(\mbox{D}\left( \sin( g(x) ) \right) = \cos( g(x) )\cdot g'(x)\). At \(x = \pi\), \(\cos( g(\pi) )\cdot g'(\pi) \approx \cos(0.86)\cdot(-1) \approx -0.65\). \(\mbox{D}\left( g( \sin(x) ) \right) = g'( \sin(x) )\cdot\cos(x)\). At \(x = \pi\), \(g'( \sin(\pi) )\cdot \cos(\pi) = g'( 0 )\cdot (-1) \approx -2\)

The Chain Rule is a general differentiation pattern that can be used along with other general patterns like the Product and Quotient Rules.

Example \(\PageIndex{7}\)

Determine \(\mbox{D}\left( e^{3x} \cdot \sin(5x + 7) \right)\) and \(\displaystyle \frac{d}{dx} \left( \cos( x \cdot e^x ) \right)\).

Solution

The function \(e^{3x} \sin(5x + 7)\) is a product of two functions so we need the Product Rule first:
\begin{align*}\mbox{D}( e^{3x} \cdot \sin(5x + 7) ) &= e^{3x}\cdot \mbox{D}( \sin(5x + 7) ) + \sin(5x + 7) \cdot\mbox{D}( e^{3x} )\\
&= e^{3x} \cdot \cos(5x +7) \cdot  5 + \sin(5x + 7) \cdot e^{3x} \cdot 3\\ 
&= 5 e^{3x} \cos(5x + 7) + 3 e^{3x} \sin(5x + 7)\end{align*}
The function \(\cos( x \cdot e^x )\) is a composition of cosine with a product so we need the Chain Rule first:
\begin{align*}
\frac{d}{dx} \left( \cos( x \cdot e^x ) \right) &= -\sin( x \cdot e^x)\cdot \frac{d}{dx} ( x \cdot e^x)\\
&= -\sin( x e^x )\cdot\left( x \cdot \frac{d}{dx} \left( e^x\right) + e^x \cdot \frac{d}{dx}\left( x \right)\right)\\
&= -\sin(x e^x) \cdot \left( x e^x + e^x\right)
\end{align*}
We could also write this last answer as \(-(x+1)e^x\sin(e^x)\).

Sometimes we want to differentiate a composition of more than two functions. We can do so if we proceed in a careful, step-by-step way.

Example \(\PageIndex{8}\)

Find \(\mbox{D}( \sin(\sqrt{x^3 + 1}))\).

Solution

The function \(\sin(\sqrt{x^3 + 1})\) can be viewed as a composition \(f\circ g\) of \(f(x) = \sin(x)\) and \(g(x) = \sqrt{x^3 + 1}\). Then:
\begin{align*}(\sin(\sqrt{x^3+ 1}))' &= f'( g(x) ) \cdot g'(x) = \cos( g(x) ) \cdot g '(x)\\
&= \cos(\sqrt{x^3 + 1}) \cdot \mbox{D}(\sqrt{x^3 + 1} )\end{align*}
For the derivative of \(\sqrt{x^3 + 1}\), we can use the Chain Rule again or its special case, the Power Rule: 
\begin{align*}\mbox{D}(\sqrt{x^3+1}) &= \mbox{D}( (x^3 + 1)^{\frac12} ) = \frac12 (x^3+1)^{-\frac12} \cdot \mbox{D}( x^3 + 1 )\\
&= \frac12 (x^3+1)^{-\frac12} \cdot 3x^2\end{align*}
Finally, \(\displaystyle \mbox{D}\left(\sin(\sqrt{x^3+ 1})\right) = \cos(\sqrt{x^3 + 1}) \cdot \frac12 (x^3+1)^{-\frac12} \cdot 3x^2\), which can be rewritten as \(\displaystyle \frac{3x^2 \cos(\sqrt{x^3+1})}{2\sqrt{x^3+1}}\).

This example was more complicated than the earlier ones, but it is just a matter of applying the Chain Rule twice, to a composition of a composition. If you proceed step by step and don’t get lost in the details of the problem, these multiple applications of the Chain Rule are relatively straightforward.

We can also use the Leibniz form of the Chain Rule for a composition of more than two functions. If \(y = \sin(\sqrt{x^3 + 1})\), then \(y = \sin(u)\) with \(u = \sqrt{w}\) and \(w = x^3 + 1\). The Leibniz form of the Chain Rule says:
\begin{align*}\frac{dy}{dx} &= \frac{dy}{du} \cdot \frac{du}{dw} \cdot \frac{dw}{dx} = \cos(u) \cdot \frac{1}{2\sqrt{w}} \cdot 3x^2\\
&= \cos(\sqrt{x^3+1}) \cdot \frac{1}{2\sqrt{x^3+1}} \cdot 3x^2\end{align*}
which agrees with our previous answer.

Practice \(\PageIndex{6}\)

1. Find \(\mbox{D}( \sin( \cos( 5x ) ) )\).
2. For \(\displaystyle y = e^{\cos(3x)}\), find \(\frac{dy}{dx}\).

Answer

\(\mbox{D}\left( \sin( \cos(5x) ) \right) = \cos( \cos(5x) )\cdot \mbox{D}( \cos(5x) ) = \cos( \cos(5x) )\cdot( -\sin(5x) )\cdot \mbox{D}( 5x ) = - 5\cdot\sin(5x)\cdot\cos( \cos(5x) )\)

 \(\displaystyle \frac{d}{dx} \left(e^{\cos(3x)}\right) = e^{\cos(3x)} \cdot\mbox{D}( \cos(3x) ) = e^{\cos(3x)} ( -\sin(3x) )\mbox{D}( 3x ) = -3\cdot\sin(3x)\cdot e^{\cos(3x)}\)

The Chain Rule and Tables of Derivatives

With the Chain Rule, the derivatives of all sorts of strange and wonderful functions become available. If we know \(f'\) and \(g'\), then we also know the derivatives of their composition: \(( f( g(x) )' = f'( g(x) )\cdot g'(x)\).

We have begun to build a list of derivatives of “basic” functions, such as \(x^n\), \(\sin(x)\) and \(e^x\). We will continue to add to that list later in the course, but if we peek ahead at the rest of that list — spoiler alert! — to (for example) see that \(\displaystyle \mbox{D}(\arctan(x)) = \frac{1}{1+x^2}\), then we can use the Chain Rule to compute derivatives of compositions of those functions.

Example \(\PageIndex{9}\)

Given that \(\displaystyle \mbox{D}( \arcsin( x ) ) = \frac{1}{\sqrt{1-x^2}}\), compute the derivatives \(\mbox{D}( \arcsin( 5x ) )\) and \(\displaystyle \frac{d}{dx}\left( \arcsin( e^x) \right)\).

Solution

Write \(\arcsin( 5x )\) as the composition of \(f(x) = \arcsin(x)\) with \(g(x) = 5x\). We know \(g'(x) = 5\) and \(\displaystyle f'(x) = \frac{1}{\sqrt{1-x^2}}\), so we have \(\displaystyle f'( g(x) ) = \frac{1}{\sqrt{1 - ( g(x) )^2}} = \frac{1}{\sqrt{1 - 25x^2}}\). Then:\[\mbox{D}( \arcsin( 5x ) ) = f'( g(x) )\cdot g'(x) = \frac{1}{\sqrt{1 - ( 5x )^2}} \cdot 5 = \frac{5}{\sqrt{1 - 25x^2}}\nonumber\]
We can write \(y = \arcsin( e^x )\) as \(y = \arcsin( u )\) with \(u = e^x\), and we know that \(\displaystyle \frac{dy}{du} = \frac{1}{\sqrt{1-u^2}}\) and \(\displaystyle \frac{du}{dx} = e^x\) so:\[\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx} =  \frac{1}{\sqrt{1-u^2}} \cdot e^x = \frac{e^x}{\sqrt{1-e^{2x}}}\nonumber\]We can generalize this result to say that \(\displaystyle \mbox{D}( \arcsin( f(x) ) ) = \frac{f'(x)}{\sqrt{1 - ( f(x) )^2}}\) or, in Leibniz notation, \(\displaystyle \frac{d}{du} ( \arcsin( u ) ) =\frac{1}{\sqrt{1 - u^2}} \cdot \frac{du}{dx}\)

Practice \(\PageIndex{7}\)

Given that \(\displaystyle \mbox{D}( \arctan( x ) ) = \frac{1}{1 + x^2}\), compute the derivatives \(\mbox{D}( \arctan( x^3 ) )\) and \(\displaystyle \frac{d}{dx}\left( \arctan( e^x) \right)\).

Answer

\(\displaystyle \mbox{D}\left( \arctan( x^3 ) \right) = \frac{1}{1 + (x^3)^2} \cdot \mbox{D}( x^3) = \frac{3x^2}{1 + x^6}\)

 \(\displaystyle \frac{d}{dx} \left( \arctan( e^x) \right) = \frac{1}{1 + ( e^x)^2}\cdot\mbox{D}( e^x) = \frac{e^x}{1 + e^{2x}}\)

Appendix D at the end of this book shows the derivative patterns for a variety of functions. You may not know much about some of the functions, but with the given differentiation patterns and the Chain Rule you should be able to calculate derivatives of compositions that involve these new functions. It is just a matter of following the pattern.

Practice \(\PageIndex{8}\)

Use the patterns \(\mbox{D}( \sinh(x) ) = \cosh(x)\) and \(\mbox{D}( \ln(x) ) = \frac{1}{x}\) to determine:

1. \(\mbox{D}( \sinh( 5x - 7) )\)
2. \(\displaystyle \frac{d}{dx} \left( \ln( 3 + e^{2x}) \right)\)
3. \(\mbox{D}( \arcsin( 1 + 3x ) )\)

Answer

\(\mbox{D}( \sinh(5x - 7) ) = \cosh(5x - 7) \cdot\mbox{D}( 5x - 7 ) = 5\cdot\cosh(5x - 7)\)

 \(\displaystyle \frac{d}{dx} \left(\ln(3 + e^{2x} \right) = \frac{1}{3 + e^{2x}} \cdot\mbox{D}( 3 + e^{2x} ) = \frac{2 e^{2x}}{3 + e^{2x}}\)

 \(\displaystyle \mbox{D}( \arcsin(1 + 3x) ) = \frac{1}{\sqrt{1 - (1 + 3x)^2}} \cdot\mbox{D}( 1 + 3x ) = \frac{3}{\sqrt{1 - (1 + 3x)^2}}\)

Example \(\PageIndex{10}\)

If \(\mbox{D}( F(x) ) = e^x \cdot \sin(x)\), find \(\mbox{D}( F(5x) )\) and \(\displaystyle \frac{d}{dt}\left( F( t^3) \right)\).

Solution

\(\mbox{D}( F(5x) ) = \mbox{D}( F( g(x) )\) with \(g(x) = 5x\) and we know that \(F'(x) = e^x \cdot \sin(x)\) so:\[\mbox{D}( F(5x) ) = F'( g(x) ) \cdot g'(x) = e^{g(x)} \cdot \sin( g(x) ) \cdot 5 = e^{5x} \cdot \sin( 5x ) \cdot 5\nonumber\]With \(y = F( u )\) and \(u = t^3\) we know \(\displaystyle \frac{dy}{du} = e^u \cdot \sin(u)\) and \(\displaystyle \frac{du}{dt} = 3t^2\) so:\[\frac{dy}{dt} = \frac{dy}{du} \cdot \frac{du}{dt} = e^u \cdot \sin(u) \cdot 3t^2 = e^{t^3} \cdot \sin( t^3 ) \cdot 3t^2\nonumber\]Notice that we have eliminated the intermediate variable \(u\) (which didn’t appear in the original problem) from the final answer.

Proof of the Power Rule For Functions

We started using the Power Rule For Functions in Section 2.3. Now we can easily prove it.

Power Rule For Functions

If: \(p\) is any constant

then: \(\mbox{D}( f^p(x) ) = p \cdot f^{p-1}(x)\cdot \mbox{D}( f(x) )\).

Proof

Write \(y = f^p(x)\) as \(y = u^p\) with \(u = f(x)\). Then \(\displaystyle \frac{dy}{du} = p\cdot u^{p-1}\) and \(\displaystyle \frac{du}{dx} = f'(x)\) so:\[\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx} = p\cdot u^{p-1} \cdot f'(x) = p\cdot f^{p-1}(x)\cdot f'(x)\nonumber\] by the Chain Rule.

Problems

In Problems 1–6 , find two functions \(f\) and \(g\) so that the given function is the composition of \(f\) and \(g\).

1. \(y = ( x^3- 7x )^5\)
2. \(y = \sin^4( 3x - 8 )\)
3. \(y = \sqrt{( 2 + \sin(x) )^5}\)
4. \(\displaystyle y = \frac{1}{\sqrt{x^2 + 9}}\)
5. \(y = \left| x^2- 4 \right|\)
6. \(y = \tan(\sqrt{x})\)
7. For each function in Problems 1–6, write \(y\) as a function of \(u\) for some \(u\) that is a function of \(x\).

For Problems 8–9, use the values given in this table to determine the indicated quantities:

\(x\)	\(f(x)\)	\(g(x)\)	\(f'(x)\)	\(g'(x)\)	\((f\circ g )(x)\)	\(( f\circ g )'(x)\)
\(-2\)	\(2\)	\(-1\)	\(1\)	\(1\)
\(-1\)	\(1\)	\(2\)	\(0\)	\(2\)
\(0\)	\(-2\)	\(1\)	\(2\)	\(-1\)
\(1\)	\(0\)	\(-2\)	\(-1\)	\(2\)
\(2\)	\(1\)	\(0\)	\(1\)	\(-1\)

8. \(( f\circ g )(x)\) and \(( f\circ g )'(x)\) at \(x = 1\) and \(x=2\).
9. \(( f\circ g )(x)\) and \(( f\circ g )'(x)\) at \(x = -2\), \(-1\) and \(0\).
10. Using the figure below, estimate the values of \(g(x)\), \(g '(x)\), \((f\circ g)(x)\), \(f'( g(x) )\) and \(( f\circ g )'( x )\) at \(x = 1\).
    
11. Using the figure below, estimate the values of \(g(x)\), \(g'(x)\), \((f\circ g)(x)\), \(f'( g(x) )\) and \((f\circ g )'( x )\) at \(x = 2\).
    

In Problems 12–22, compute the derivative.

12. \(\mbox{D}\left( ( x^2 + 2x + 3 )^{87} \right)\)
13. \(\displaystyle \mbox{D}\left( \left( 1 - \frac{3}{x}\right)^4\right)\)
14. \(\displaystyle \frac{d}{dx} \left( x + \frac{1}{x}\right)^5\)
15. \(\displaystyle \mbox{D}\left( \frac{5}{\sqrt{2 + \sin(x)}}\right)\)
16. \(\displaystyle \frac{d}{dt} \left(t\cdot\sin( 3t + 2 )\right)\)
17. \(\displaystyle \frac{d}{dx}\left( x^2\cdot \sin( x^2 + 3 ) \right)\)
18. \(\displaystyle \frac{d}{dx} \left(\sin(2x)\cdot\cos(5x+1)\right)\)
19. \(\displaystyle \mbox{D}\left( \frac{7}{\cos( x^3- x )}\right)\)
20. \(\displaystyle \frac{d}{dt}\left(\frac{5}{3+e^t}\right)\)
21. \(\mbox{D}\left( e^x + e^{-x}\right)\)
22. \(\mbox{D}\left( e^x - e^{-x}\right)\)
23. An object attached to a spring is at a height of \(h(t) = 3 - \cos( 2t )\) feet above the floor \(t\) seconds after it is released.
    1. At what height was it released?
    2. Determine its height, velocity and acceleration at any time \(t\).
    3. If the object has mass \(m\), determine its kinetic energy \(K = \frac12 mv^2\) and \(\frac{dK}{dt}\) at any time \(t\).
24. An employee with \(d\) days of production experience will be able to produce approximately \(P(d) = 3 + 15( 1 - e^{-0.2d} )\) items per day.
    1. Graph \(P(d)\).
    2. Approximately how many items will a beginning employee be able to produce each day?
    3. How many items will a very experienced employee be able to produce each day?
    4. What is the marginal production rate of an employee with 5 days of experience? (Include units for your answer. What does this mean?)
25. The air pressure \(P(h)\), in pounds per square inch, at an altitude of \(h\) feet above sea level is approximately \(P(h) = 14.7 e^{-0.0000385h}\).
    1. What is the air pressure at sea level?
    2. What is the air pressure at 30,000 feet?
    3. At what altitude is the air pressure 10 pounds per square inch?
    4. If you are in a balloon that is 2,000 feet above the Pacific Ocean and is rising at 500 feet per minute, how fast is the air pressure on the balloon changing?
    5. If the temperature of the gas in the balloon remained constant during this ascent, what would happen to the volume of the balloon?

Find the indicated derivatives in Problems 26--33.

26. \(\displaystyle \mbox{D}\left( \frac{( 2x + 3 )^2}{( 5x - 7 )^3} \right)\)
27. \(\displaystyle \frac{d}{dz} \sqrt{1 + \cos^2( z )}\)
28. \(\mbox{D}\left( \sin( 3x + 5 ) \right)\)
29. \(\displaystyle \frac{d}{dx} \tan( 3x + 5 )\)
30. \(\displaystyle \frac{d}{dt} \cos( 7t^2)\)
31. \(\mbox{D}\left( \sin( \sqrt{x + 1} ) \right)\)
32. \(\mbox{D}\left( \sec( \sqrt{x + 1} ) \right)\)
33. \(\displaystyle \frac{d}{dx} \left( e^{\sin(x)}\right)\)

In Problems 34–37 , calculate \(f'(x) \cdot x'(t)\) when \(t = 3\) and use these values to determine the value of \(\displaystyle \frac{d}{dt}\left(f( x(t) )\right)\) when \(t = 3\).

34. \(f( x ) = \cos( x )\), \(x = t^2- t + 5\)
35. \(f( x ) = \sqrt{x}\), \(\displaystyle x = 2 + \frac{21}{t}\)
36. \(f( x ) = e^x\), \(x = \sin( t )\)
37. \(f( x ) = \tan^3( x )\), \(x = 8\)

In Problems 38–43, find a function that has the given function as its derivative. (You are given a function \(f'(x)\) and are asked to find a corresponding function \(f(x)\).)

38. \(f'(x) = ( 3x + 1 )^4\)
39. \(f'(x) = ( 7x - 13 )^{10}\)
40. \(f'(x) = \sqrt{3x - 4}\)
41. \(f'(x) = \sin( 2x - 3 )\)
42. \(f'(x) = 6e^{3x}\)
43. \(\displaystyle f'(x) = \cos(x) e^{\sin(x)}\)

If two functions are equal, then their derivatives are also equal. In Problems 44–47 , differentiate each side of the trigonometric identity to get a new identity.

44. \(\sin^2( x ) = \frac12 - \frac12 \cos( 2x )\)
45. \(\cos( 2x ) = \cos^2( x ) - \sin^2( x )\)
46. \(\sin( 2x ) = 2\sin( x )\cdot \cos( x )\)
47. \(\sin( 3x ) = 3\sin( x ) - 4\sin^3( x )\)

Derivatives of Families of Functions

So far we have emphasized derivatives of particular functions, but sometimes we want to investigate the derivatives of a whole family of functions all at once. In 48--71, \(A\), \(B\), \(C\) and \(D\) represent constants and the given formulas describe families of functions.

For Problems 48–65, calculate \(y' = \frac{dy}{dx}\).

48. \(y = Ax^3 - B\)
49. \(y = Ax^3 + Bx^2 + C\)
50. \(y = \sin( Ax + B )\)
51. \(y = \sin(Ax^2 + B)\)
52. \(y = Ax^3 + \cos( Bx )\)
53. \(y = \sqrt{A + Bx^2}\)
54. \(y = \sqrt{A - Bx^2}\)
55. \(y = A - \cos( Bx )\)
56. \(y = \cos( Ax + B )\)
57. \(y = \cos( Ax^2 + B )\)
58. \(y = A\cdot e^{Bx}\)
59. \(y = x\cdot e^{Bx}\)
60. \(y = e^{Ax} + e^{-Ax}\)
61. \(y = e^{Ax} - e^{-Ax}\)
62. \(\displaystyle y =\frac{\sin( Ax )}{x}\)
63. \(\displaystyle y = \frac{Ax}{\sin( Bx )}\)
64. \(\displaystyle y = \frac{1}{Ax + B}\)
65. \(\displaystyle y = \frac{Ax + B}{Cx + D}\)

In Problems 66–71:

1. find \(y'\)
2. find the value(s) of \(x\) so that \(y' = 0\) and
3. find \(y''\).

Typically your answer in part (b) will contain \(A\)'s, \(B\)'s and (sometimes) \(C\)'s.

66. \(y = Ax^2 + Bx + C\)
67. \(y = Ax(B-x) = ABx - Ax^2\)
68. \(y = Ax(B - x^2) = ABx - Ax^3\)
69. \(y = Ax^2 (B - x) = ABx^2 - Ax^3\)
70. \(y = Ax^2 + Bx\)
71. \(y = Ax^3 + Bx^2 + C\)

In Problems 72–83, use the differentiation patterns \(\displaystyle \mbox{D}( \arctan( x ) ) = \frac{1}{1 + x^2}\), \(\displaystyle \mbox{D}( \arcsin( x ) ) = \frac{1}{\sqrt{1-x^2}}\) and \(\displaystyle \mbox{D}( \ln( x ) ) = \frac{1}{x}\). We have not derived the derivatives for these functions (yet), but if you are handed the derivative pattern then you should be able to use that pattern to compute derivatives of associated composite functions.

72. \(\mbox{D}\left( \arctan( 7x ) \right)\)
73. \(\mbox{D}\left( \arctan( x^2) \right)\)
74. \(\displaystyle \frac{d}{dt} \left( \arctan( \ln(t) ) \right)\)
75. \(\displaystyle \frac{d}{dx} \left( \arctan( e^x ) \right)\)
76. \(\displaystyle \frac{d}{dw} \left( \arcsin( 4w ) \right)\)
77. \(\displaystyle \frac{d}{dx} \left( \arcsin( x^3)\right)\)
78. \(\mbox{D}\left( \arcsin( \ln(x) ) \right)\)
79. \(\mbox{D}\left( \arcsin( e^t) \right)\)
80. \(\mbox{D}\left( \ln( 3x + 1) \right)\)
81. \(\mbox{D}\left( \ln( \sin(x) ) \right)\)
82. \(\displaystyle \frac{d}{dx}\left( \ln( \arctan(x) ) \right)\)
83. \(\displaystyle \frac{d}{ds}\left( \ln( e^s) \right)\)
84. To prove the Chain Rule, assume \(g(x)\) is differentiable at \(x=a\) and \(f(x)\) is differentiable at \(x = g(a)\). We need to show that\[\lim_{x\to a}\,\frac{f(g(x))-f(g(a))}{x-a}\nonumber\]exists and is equal to \(f'(g(a))\cdot g'(a)\). To do this, define a new function \(F\) as:\[F(y) = \left\{ \begin{array}{rl} { \frac{f(y)-f(g(a))}{y-g(a)} } & { \text{if } y \neq g(a) } \\ { f'(g(a)) } & { \text{if } y = g(a) } \end{array}\right.\nonumber\]and justify each of the following statements.
    1. \(F(y)\) is continuous at \(y = g(a)\) because:\[\lim_{y\to g(a)} \, F(y) = \lim_{y\to g(a)} \, \frac{f(y)-f(g(a))}{y-g(a)} = F(g(a))\nonumber\]
    2. By considering separately the cases \(g(x) = g(a)\) and \(g(x) \neq g(a)\):\[\frac{f(g(x))-f(g(a))}{x-a} = F(g(x)) \cdot \frac{g(x)-g(a)}{x-a}\nonumber\]for all \(x \neq a\).
    3. \(\displaystyle \lim_{x\to a}\,\frac{f(g(x))-f(g(a))}{x-a} = \lim_{x\to a}\, F(g(x)) \cdot \frac{g(x)-g(a)}{x-a}\)
    4. \(\displaystyle \lim_{x\to a}\, F(g(x)) \cdot \frac{g(x)-g(a)}{x-a} = F(g(a)) \cdot g'(a)\)
    5. \(\displaystyle \lim_{x\to a}\,\frac{f(g(x))-f(g(a))}{x-a} = f'(g(a))\cdot g'(a)\)
    6. \(\left(f\circ g\right)'(a) = f'(g(a))\cdot g'(a)\)