2.6: Related Rates

Last updated
Save as PDF

Page ID: 212016

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\dsum}{\displaystyle\sum\limits} $

$ \newcommand{\dint}{\displaystyle\int\limits} $

$ \newcommand{\dlim}{\displaystyle\lim\limits} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$\newcommand{\longvect}{\overrightarrow}$

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Throughout the next several sections we’ll look at a variety of applications of derivatives. Probably no single application will be of interest or use to everyone, but at least some of them should be useful to you. Applications also reinforce what you have been practicing: they require that you recall what a derivative means and require you to use the differentiation techniques covered in the last several sections. Most people gain a deeper understanding and appreciation of a tool as they use it, and differentiation is both a powerful concept and a useful tool.

The Derivative as a Rate of Change

In Section 2.1, we discussed several interpretations of the derivative of a function. Here we will examine the “rate of change of a function” interpretation. If several variables or quantities are related to each other and some of the variables are changing at a known rate, then we can use derivatives to determine how rapidly the other variables must be changing.

Example $\PageIndex{1}$

The radius of a circle is increasing at a rate of 10 feet each second:

$Three concentric circles: a black one, with radius r indicated, inside a blue one inside a red one.$

and we want to know how fast the area of the circle is increasing when the radius is 5 feet. What can we do?

Solution

We could get an approximate answer by calculating the area of the circle when the radius is 5 feet:\[A = \pi r^2 = \pi(5\mbox{ feet})^2 \approx 78.6 \, \mbox{ feet}^2\]and the area 1 second later when the radius is 10 feet larger than before:\[A = \pi r^2 = \pi(15\mbox{ feet})^2 \approx 706.9 \mbox{ feet}^2\]and then computing:\[\frac{\Delta\mbox{area}}{\Delta\mbox{time}} = \frac{706.9\mbox{ feet}^2 - 78.6\mbox{ feet}^2}{1\mbox{ second}} = 628.3 \, \frac{\mbox{ft}^2}{\mbox{sec}}\]This approximate answer represents the average change in area during the 1-second period when the radius increased from 5 feet to 15 feet. It is also the slope of the secant line through the points $P$ and $Q$ in the figure below:

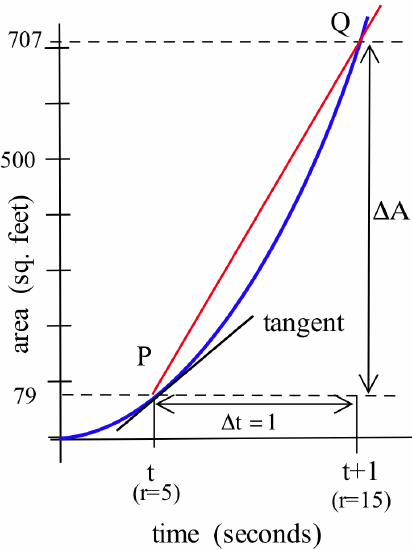
$A graph of a concave-up, increasing blue curve passing through P(t,79) and Q(t+1,707) along with a red line segment passing through P and Q and a black line segment tangent to the blue curve at P. The horizontal axis is labeled 'time (seconds)' and the vertical axis 'area (sq. feet).' The horizontal diatnce between P and Q is denoted by a double arrow labeled 'Delta t = 1' and the vertical distance by a double arrow labeled 'Delta A.' The horizontal axis is marked with 't (r=5)' below P and 't+1 (r=15)' below Q. There are two dashed horizontal lines at heights of 79 and 707, passing through P and Q, respectively.$

and it is clearly not a very good approximation of the instantaneous rate of change of the area, the slope of the tangent line at the point $P$.

We could get a better approximation by calculating $\displaystyle \frac{\Delta A}{\Delta t}$ over a shorter time interval, say $\Delta t = 0.1$ seconds. In this scenario, the original area is still $78.6$ ft$^2$ but the new area (after $t = 0.1$ seconds has passed) is $A = \pi (6\mbox{ feet})^2 \approx 113.1$ ft$^2$ (why is the new radius $6$ feet?) so:\[\frac{\Delta A}{\Delta t} = \frac{113.1\mbox{ feet}^2 - 78.6\mbox{ feet}^2}{0.1\mbox{ second}} = 345 \frac{\mbox{ft}^2}{\mbox{sec}}\]This is the slope of the secant line through the points $P$ and $Q$ in the figure below:

$A graph of a concave-up, increasing blue curve passing through P(t,79) and Q(t+0.1,113) along with a red line segment passing through P and Q, labeled 'secant,' and a black line segment (labeled 'tangent') that is tangent to the blue curve at P. The horizontal axis is labeled 'time (seconds)' and the vertical axis 'area (square feet).' The horizontal distance between P and Q is denoted by a double arrow labeled 'Delta t = 0.1' and the vertical distance by a double arrow labeled 'Delta A.' The horizontal axis is marked with 't (r=5)' below P and 't+1 (r=6)' below Q. There are two dashed horizontal lines at heights of 79 and 113, passing through P and Q, respectively.$

which represents a much better approximation of the slope of the tangent line at $P$ — but it is still only an approximation. Using derivatives, we can get an exact answer without doing very much work at all.

We know that the two variables in this problem, the radius $r$ and the area $A$, are related to each other by the formula $A = \pi r^2$. We also know that both $r$ and $A$ are changing over time, so each of them is a function of an additional variable $t$ (time, in seconds): $r(t)$ and $A(t)$.

We want to know the rate of change of the area “when the radius is 5 feet” so if $t = 0$ corresponds to the particular moment in time when the radius is 5 feet, we can write $r(0) = 5$.

The statement that “the radius is increasing at a rate of 10 feet each second” can be translated into a mathematical statement about the rate of change, the derivative of $r$ (radius) with respect to $t$ (time): if $t=0$ corresponds to the moment when the radius is 5 feet, then $\displaystyle r'(0) = \frac{dr}{dt} = 10$ ft/sec.

The question about the rate of change of the area is a question about $\displaystyle A'(t) = \frac{dA}{dt}$.

Collecting all of this information …

variables: $r(t)$ = radius at time $t$, $A(t)$ = area at time $t$
we know: $r(0) = 5$ feet and $r'(0) = 10$ ft/sec
we want to know: $A'(0)$, the rate of change of area with respect to time at the moment when $r = 5$ feet
connecting equation: $A = \pi r^2$ or $A(t) = \pi\left[r(t)\right]^2$

To find $A'(0)$ we must first find $A'(t)$ and then evaluate this derivative at $t = 0$. Differentiating both sides of the connecting equation, we get:\[A(t) = \pi\left[r(t)\right]^2 \Rightarrow A'(t) = 2\pi\left[r(t)\right]^1\cdot r'(t) \Rightarrow A'(t) = 2\pi \cdot r(t) \cdot r'(t)\](Notice that we have used the Power Rule for Functions — or, more generally, the Chain Rule — because the area is a function of the radius, which is a function of time.)

Now we can plug in $t=0$ and use the information we know:\[A'(0) = 2\pi \cdot r(0) \cdot r'(0) = 2\pi \cdot 5 \cdot 10 = 100\pi\]When the radius is 5 feet, the area is increasing at $100\pi$ ft$^2$/sec $\approx 314.2$ square feet per second.

Before considering other examples, let’s review the solution to the previous example. The statement “the radius is increasing at a rate of 10 feet each second” implies that this rate of change is the same at $t=0$ (the moment in time we were interested in) as at any other time during this process, say $t = 1.5$ or $t = 98$: $r'(0) = r'(1.5) = r'(98) = 10$. But we only used the fact that $r'(0) = 10$ in our solution. (We should take care in future problems to consider whether the information we are given about rates of change holds true all the time or just at a particular moment in time. That didn't matter in our first example, but it might in other situations.)

Next, notice that we let $t=0$ correspond to the particular moment in time the question asked about (the moment when $r = 5$). But this choice was arbitrary: we could have let this moment correspond to $t = 2.8$ or $t = 7\pi$ and the eventual answer would have been the same.

Finally, notice that we explicitly wrote each variable (and their derivatives) as a function of the time variable, $t$: $A(t)$, $r(t)$, $A'(t)$ and $r'(t)$. Consequently, we used the composition form of the Chain Rule:\[(A\circ r)'(t) = A'(r(t))\cdot r'(t)\]Let’s redo the previous example using the Leibniz form of the Chain Rule, keeping the above observations in mind.

Example $\PageIndex{1}$

Solution

We want to know the rate of change of the area “when the radius is 5 feet,” which translates to evaluating $\displaystyle \frac{dA}{dt}$ at the moment when $r = 5$. We write this in Leibniz notation as:\[\left.\frac{dA}{dt}\right|_{r = 5}\]The statement that “the radius is increasing at a rate of 10 feet each second” translates into $\displaystyle \frac{dr}{dt} = 10$. From the connecting equation $A = \pi r^2$ we know that $\displaystyle \frac{dA}{dr} = 2\pi r$. Furthermore,the Chain Rule tells us that:\[\frac{dA}{dt} = \frac{dA}{dr}\cdot \frac{dr}{dt}\]We know that $\displaystyle \frac{dA}{dr} = 2\pi r$ and $\displaystyle \frac{dr}{dt} = 10$ are always true, so we can rewrite the Chain Rule statement above as:\[\frac{dA}{dt} = 2\pi r \cdot 10 = 20\pi r\]Finally, we evaluate both sides at the moment in time we are interested in (the moment when $r=5$):\[\left.\frac{dA}{dt}\right|_{r = 5} = 20\pi r \Big|_{r = 5} = 20\pi \cdot 5 = 100\pi \approx 314.2\]which is the same answer we found in the original solution.

The key steps in finding the rate of change of the area of the circle were:

write the known information in a mathematical form, expressing rates of change as derivatives: $\displaystyle \frac{dr}{dt} = 10$ ft/sec
write the question in a mathematical form: $\displaystyle \frac{dA}{dt} =$ ?
find an equation connecting or relating the variables: $A = \pi r^2$
differentiate both sides of the connecting equation using the Chain Rule (and other differentiation patterns as necessary): $\displaystyle \frac{dA}{dt} = \frac{dA}{dr} \frac{dr}{dt}$
substitute all of the known values that are always true into the equation resulting from the previous step and (if necessary) solve for the desired quantity in the resulting equation: $\displaystyle \frac{dA}{dt} = 2\pi r \cdot 10$
substitute all of the known values that are true at the particular moment in time the question asks about into the equation resulting from the previous step: $\displaystyle \frac{dA}{dt} \Big|_{r = 5} = 2\pi r \cdot 10 \Big|_{r=5} = 100\pi$

Example $\PageIndex{2}$

Divers’ lives depend on understanding situations involving related rates. In water, the pressure at a depth of $x$ feet is approximately $\displaystyle P(x) = 15\left( 1 + \frac{x}{33}\right)$ pounds per square inch (compared to approximately $P(0) = 15$ pounds per square inch at sea level). Volume is inversely proportional to the pressure, $\displaystyle V = \frac{k}{P}$, so doubling the pressure will result in half the original volume. Remember that volume is a function of the pressure: $V = V(P)$.

Suppose a diver's lungs, at a depth of 66 feet, contained 1 cubic foot of air and the diver ascended to the surface without releasing any air. What would happen?
If a diver started at a depth of 66 feet and ascended at a rate of 2 feet per second, how fast would the pressure be changing?

(Dives deeper than 50 feet also involve a risk of the “bends,” or decompression sickness, if the ascent is too rapid. Tables are available that show the safe rates of ascent from different depths.)

Solution

The diver would risk rupturing his or her lungs. The 1 cubic foot of air at a depth of 66 feet would be at a pressure of $P(66) = 15\left(1 + \frac{66}{33}\right) = 45$ pounds per square inch (psi). Because the pressure at sea level, $P(0) = 15$ psi, is only $\frac13$ as great, each cubic foot of air would expand to 3 cubic feet, and the diver's lungs would be in danger. Divers are taught to release air as they ascend to avoid this danger.
The diver is ascending at a rate of 2 feet/second so the rate of change of the diver's depth with respect to time is $\displaystyle \frac{dx}{dt} = -2$ ft/s. (Why is this rate of change negative?) The pressure is $P = 15\left( 1 + \frac{x}{33}\right) = 15 + \frac{15}{33} x$, a function of $x$, so using the Chain Rule:\[\frac{dP}{dt} = \frac{dP}{dx} \cdot \frac{dx}{dt} = \frac{15}{33} \, \frac{\mbox{psi}}{\mbox{ft}} \cdot \left(-2 \, \frac{\mbox{ft}}{\mbox{sec}}\right) = -\frac{30}{33} \, \frac{\mbox{psi}}{\mbox{sec}} \approx -0.91 \, \frac{\mbox{psi}}{\mbox{sec}}\]The rates of change in this problem are constant (they hold true at any moment in time during the ascent) so we are done.

Example $\PageIndex{3}$

The height of a cylinder is increasing at 7 meters per second and the radius is increasing at 3 meters per second. How fast is the volume changing when the cylinder is 5 meters high and has a radius of 6 meters?

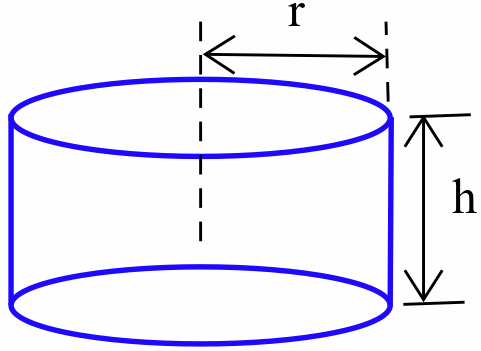
$A blue right circular cylinder with height h and radius r denoted by double arrows.$

Solution

First we need to translate our known information into a mathematical format. The height and radius are given: at the particular moment in time the question asks about, $h =$ height $= 5$ m and $r =$ radius $= 6$ m. We are also told how fast $h$ and $r$ are changing at this moment in time: $\frac{dh}{dt} = 7$ m/sec and $\frac{dr}{dt} = 3$ m/sec. Finally, we are asked to find $\frac{dV}{dt}$, and we should expect the units of $\frac{dV}{dt}$ to be the same as $\frac{\Delta V}{\Delta t}$, which are m$^3$/sec.

variables: $h(t) =$ height at time $t$ seconds, $r(t) =$ radius at time $t$, $V(t) =$ volume at time $t$.
we know: at a particular moment in time, $h = 5$ m, $\frac{dh}{dt} = 7$ m/sec, $r = 6$ m and $\frac{dr}{dt} = 3$ m/sec
we want to know: $\frac{dV}{dt}$ at this particular moment in time

We also need an equation that relates the variables $h$, $r$ and $V$ (all of which are functions of time $t$) to each other:

connecting equation: $V = \pi r^2h$

Differentiating each side of this equation with respect to $t$ (remembering that $h$, $r$ and $V$ are functions of $t$), we have: \begin{align*}\frac{dV}{dt} = \frac{d}{dt}\left(\pi r^2 h\right) &= \pi r^2 \cdot \frac{dh}{dt} + h\cdot \frac{d}{dt}\left(\pi r^2\right)\\ &= \pi r^2 \cdot \frac{dh}{dt} + h\cdot 2\pi r \cdot \frac{dr}{dt}\end{align*} using the Product Rule (on the product $\pi r^2 \cdot h$) and the Power Rule for Functions (on $\pi r^2$, remembering that $r$ is actually a function of $t$).

The rest of the solution just involves substituting values and doing some arithmetic. At the particular moment in time we're interested in: \begin{align*}\frac{dV}{dt} &= \pi \cdot 6^2 \, \mbox{m}^2 \cdot 7 \, \frac{\mbox{m}}{\mbox{sec}} + 5 \,\mbox{m} \cdot 2\pi \cdot 6 \,\mbox{m} \cdot 3 \, \frac{\mbox{m}}{\mbox{sec}}\\ &= 432\pi \, \frac{\mbox{m}^3}{\mbox{sec}} \approx 1357.2 \, \frac{\mbox{m}^3}{\mbox{sec}}\end{align*} The volume of the cylinder is increasing at a rate of 1,357.2 cubic meters per second. (It is always encouraging when the units of our answer are the ones we expect.)

Practice $\PageIndex{1}$

How fast is the surface area of the cylinder changing in Example $\PageIndex{3}$?

$A right circular cylinder with height h denoted by a double arrow and radius r denoted by an arrow. The sides of the cylinder a blue line segments and the top and bottom indicated by red circles. Dashed black lines connect the cylinder to a rectangle with blue sides of height h, and red top and bottom, above and below which are red circles labeled 'pi r^2.'$

Assume that $h$, $r$, $\frac{dh}{dt}$ and $\frac{dr}{dt}$ have the same values as in the example and use the figure above to help you determine an equation relating the surface area of the cylinder to the variables $h$ and $r$. The cylinder includes a top and bottom.

Answer: The surface area is $S = 2\pi rh + 2\pi r^2$. From the Example, we know that $\frac{dh}{dt} = 7$ m/sec and $\frac{dr}{dt} = 3$ m/sec, and we want to know how fast the surface area is changing
when $h = 5$ m and $r = 6$ m.
\begin{align*}\frac{dS}{dt} &= 2\pi r \cdot \frac{dh}{dt} + 2\pi \frac{dr}{dt} \cdot h + 2\pi \cdot 2r\cdot \frac{dr}{dt}\\
&= 2\pi(6 \, \mbox{m})\left( 7 \, \frac{\mbox{m}}{\mbox{sec}}\right) + 2\pi\left(3 \frac{\mbox{m}}{\mbox{sec}}\right)(5 m) + 2\pi\left(2\cdot
6 \, \mbox{m}\right)\left(3 \, \frac{\mbox{m}}{\mbox{sec}}\right)\\ &= 186\pi \, \frac{\mbox{m}^2}{\mbox{sec}} \approx 584.34 \, \frac{\mbox{m}^2}{\mbox{sec}}\end{align*} (Note that the units represent a rate of change of area.)

Practice $\PageIndex{2}$

How fast is the volume of the cylinder in Practice $\PageIndex{1}$ changing if the radius is decreasing at a rate of 3 meters per second? (The height, radius and rate of change of the height are the same as in Example $\PageIndex{3}$: 5 m, 6 m and 7 m/sec respectively.)

Answer: The volume is $V = %\left(\mbox{area of the bottom}\right)\left(\mbox{height}\right) = \pi r^2 h$. We know that $\frac{dr}{dt} = -3$ m/sec and that $h = 5$ m, $r = 6$ m and $\frac{dh}{dt} = 7$ m/sec.
\begin{align*}\frac{dV}{dt} &= \pi r^2\cdot \frac{dh}{dt} + \pi\cdot 2r \cdot \frac{dr}{dt}\\
&= \pi(6 \, \mbox{m})^2\left(7 \, \frac{\mbox{m}}{\mbox{sec}}\right) + \pi(2\cdot 6 \, \mbox{m})\left(-3 \, \frac{\mbox{m}}{\mbox{sec}}\right)\\ &= 72\pi \, \frac{\mbox{m}^3}{\mbox{sec}} \approx 226.19 \, \frac{\mbox{m}^3}{\mbox{sec}}\end{align*} (Note that the units represent a rate of change of volume.)

Usually, the most difficult part of Related Rates problems is to find an equation that relates or connects all of the variables. In the previous problems, the relating equations required a knowledge of geometry and formulas for areas and volumes (or knowing where to look them up). Other Related Rates problems may require information about similar triangles, the Pythagorean Theorem or trigonometric identities: the information required varies from problem to problem.

It is a good idea — a very good idea — to draw a picture of the physical situation whenever possible. It is also a good idea, particularly if the problem is very important (your next raise depends on getting the right answer), to calculate at least one approximate answer as a check of your exact answer.

Example $\PageIndex{4}$

Water is flowing into a conical tank at a rate of 5 m$^3$/sec. If the radius of the top of the cone is 2 m, the height is 7 m, and the depth of the water is 4 m, then how fast is the water level rising?

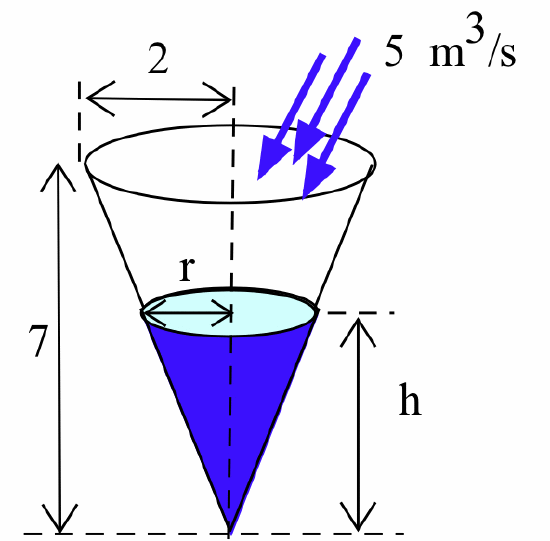
$A right circular cone with vertex pointing down. Double arrows indicate the height to be 7 and the radius to be h. Three blue arrows represent water flowing into the top, labeled '5 m^3/s.' Water fills the cone from bottom to approximately halfway up the cone. Double arrows indicate the height of the water to be h and the radius to be r.$

Solution

Let’s define our variables to be $h =$ height (or depth) of the water in the cone and $V =$ the volume of the water in the cone. Both $h$ and $V$ are changing, and both of them are functions of time $t$. We are told in the problem that $h = 4$ m and $\frac{dV}{dt} = 5$ m$^3$/sec, and we are asked to find $\frac{dh}{dt}$. We expect that the units of $\frac{dh}{dt}$ will be the same as $\frac{\Delta h}{\Delta t}$, which are meters/second.

variables: $h(t) =$ height at time $t$ seconds, $r(t) =$ radius of the top surface of the water at time $t$, $V(t)$ = volume of water at time $t$
we know: $\frac{dV}{dt} = 5$ m$^3$/sec (always true) and $h = 4$ m (at a particular moment)
we want to know: $\frac{dh}{dt}$ at this particular moment

Unfortunately, the equation for the volume of a cone, $V = \frac13 \pi r^2 h$, also involves an additional variable $r$, the radius of the cone at the top of the water. This is a situation in which a picture can be a great help by suggesting that we have a pair of similar triangles:\[\frac{r}{h} = \frac{\mbox{top radius}}{\mbox{total height}} = \frac{2\mbox{ m}}{7\mbox{ m}} = \frac27 \quad \Rightarrow \quad r = \frac27 h\]Knowing this, we can rewrite the volume of the water contained in the cone, $V = \frac13 \pi r^2 h$, as a function of the single variable $h$:

connecting equation: $\displaystyle V = \frac13 \pi r^2 h = \frac13 \pi \left(\frac27 h\right)^2 h = \frac{4}{147}\pi h^3$

The rest of the solution is reasonably straightforward.\[\frac{dV}{dt} = \frac{dV}{dh} \cdot \frac{dh}{dt} = \frac{d}{dh}\left(\frac{4}{147}\pi h^3\right) \cdot \frac{dh}{dt}\]We know $\displaystyle \frac{dV}{dt} = 5$ always holds, and the derivative is easy to compute:\[5 = \frac{4}{49}\pi h^2 \cdot \frac{dh}{dt}\]At the particular moment in time we want to know about (when $h = 4$):\[5 = \frac{4}{49}\pi h^2\Big|_{h=4} \cdot \frac{dh}{dt}\Big|_{h=4} \quad \Rightarrow \quad 5 = \frac{64\pi}{49} \cdot \frac{dh}{dt}\Big|_{h=4}\]and we can now solve for the quantity of interest:\[\frac{dh}{dt}\Big|_{h=4} = \frac{5}{\frac{64\pi}{49}} = \frac{245}{64\pi} \approx 1.22 \, \frac{\mbox{m}}{\mbox{sec}}\]This example was a bit more challenging because we needed to use similar triangles to get an equation relating $V$ to $h$ and because we eventually needed to do some arithmetic to solve for $\displaystyle \frac{dh}{dt}$.

Practice $\PageIndex{3}$

A rainbow trout has taken the fly at the end of a 60-foot fishing line, and the line is being reeled in at a rate of 30 feet per minute. If the tip of the rod is 10 feet above the water and the trout is at the surface of the water, how fast is the trout being pulled toward the angler? (Hint: Draw a picture and use the Pythagorean Theorem.)

Answer

$A heavy black circular arc rises from the left end of a horizontal black line segment. A blue oval near the other end of the horizontal line segment is labeled 'fish.' Another line segment extends from the blue oval to the upper end of the circular arc, with its lenght labeled 'L.' A dashed vertical line (with height indiciated as 10) with double arrows extends from the intersection of the upper endpoint of the arc and the slanted line down to a point on the horizontal like, with a solid double arrow extending from that intersection point to the blue oval, its length labeled 'F.'$

We know $\frac{dL}{dt} = -30\,\frac{\mbox{ft}}{\mbox{min}}$ (always true); $F$ represents the distance from the fish to a point directly below the tip of the rod, and the distance from that point to the angler remains constant, so $\frac{dF}{dt}$ will equal the rate at which the fish is moving toward the angler. We want to know $\left. \frac{dF}{dt}\right|_{L = 60}$. The Pythagorean Theorem connects $F$ and $L$: $F^2 + 10^2 = L^2$. Differentiating with respect to $t$ and using the Power Rule for Functions:\[2F\cdot \frac{dF}{dt} + 0 = 2L\cdot \frac{dL}{dt} \quad \Rightarrow \quad \frac{dF}{dt} = \frac{L}{F} \cdot \frac{dL}{dt}\]At a particular moment in time, $L = 60 \Rightarrow F^2+10^2 = 60^2 \Rightarrow F = \sqrt{3600-100} = \sqrt{3500} = 10\sqrt{35}$ so:\[\frac{dF}{dt}\Big|_{L=60} = -30 \cdot \frac{60}{10\sqrt{35}} = -\frac{180}{\sqrt{35}} \approx -30.43 \, \frac{\mbox{ft}}{\mbox{min}}\]

Example $\PageIndex{5}$

When rain is falling vertically, the amount (volume) of rain collected in a cylinder is proportional to the area of the opening of the cylinder.

$A blue right circular cylinder with radius r indicated by a black arrow and a red right circular cylinder with radius R indicated by a black arrow sit next to each other on a black horizontal line. Downward-pointing arros labeled 'rain' are above the cylinders.$

If you place a narrow cylindrical glass and a wide cylindrical glass out in the rain:

which glass will collect water faster?
in which glass will the water level rise faster?

Solution

Let’s assume that the smaller glass has a radius of $r$ and the larger glass has a radius of $R$, so that $R > r$. The areas of their openings are $\pi r^2$ and $\pi R^2$, respectively. Call the volume of water collected in each glass $v$ (for the smaller glass) and $V$ (for the larger glass).

FIGURE

The smaller glass will collect water at the rate $\displaystyle \frac{dv}{dt} = K\cdot \pi r^2$ and the larger at the rate $\displaystyle \frac{dV}{dt} = K\cdot \pi R^2$ so $\displaystyle \frac{dV}{dt} > \frac{dv}{dt}$ and the larger glass will collect water faster than the smaller glass.
The volume of water in each glass is a function of the radius of the glass and the height of the water in the glass: $v = \pi r^2 h$ and $V = \pi R^2 H$ where $h$ and $H$ are the heights of the water levels in the smaller and larger glasses, respectively. The heights $h$ and $H$ vary with $t$ (in other words, they are each functions of $t$) while the radii ($r$ and $R$) remain constant, so:\[\frac{dv}{dt} = \frac{d}{dt}\left( \pi r^2 h \right) = \pi r^2 \frac{dh}{dt} \quad \Rightarrow \quad \frac{dh}{dt} = \frac{\frac{dv}{dt}}{\pi r^2} = \frac{K\pi r^2}{\pi r^2} = K\]Similarly:\[\frac{dV}{dt} = \frac{d}{dt}\left( \pi R^2 H \right) = \pi R^2 \frac{dH}{dt} \ \Rightarrow \ \frac{dH}{dt} = \frac{\frac{dV}{dt}}{\pi R^2} = \frac{K\pi R^2}{\pi R^2} = K\]So $\displaystyle \frac{dh}{dt} = K = \frac{dH}{dt}$, which tells us the water level in each glass is rising at the same rate. In a one-minute period, the larger glass will collect more rain, but the larger glass also requires more rain to raise its water level by a fixed amount. How do you think the volumes and water levels would change if we placed a small glass and a large plastic (rectangular) box side by side in the rain?

Problems

An expandable sphere is being filled with liquid at a constant rate from a tap (imagine a water balloon connected to a faucet). When the radius of the sphere is 3 inches, the radius is increasing at 2 inches per minute. How fast is the liquid coming out of the tap? ($V = \frac43 \pi r^3$)
The 12-inch base of a right triangle is growing at 3 inches per hour, and the 16-inch height of the triangle is shrinking at 3 inches per hour:
1. Is the area increasing or decreasing?
2. Is the perimeter increasing or decreasing?
3. Is the hypotenuse increasing or decreasing?
One hour later the right triangle in the previous problem is 15 inches long and 13 inches high:

and the base and height are changing at the same rate as in Problem 2.
1. Is the area increasing or decreasing now?
2. Is the hypotenuse increasing or decreasing?
3. Is the perimeter increasing or decreasing?
A young woman and her boyfriend plan to elope, but she must rescue him from his mother, who has locked him in his room. The young woman has placed a 20-foot long ladder against his house and is knocking on his window when his mother begins pulling the bottom of the ladder away from the house at a rate of 3 feet per second:

How fast is the top of the ladder (and the young couple) falling when the bottom of the ladder is:
1. 12 feet from the bottom of the wall?
2. 16 feet from the bottom of the wall?
3. 19 feet from the bottom of the wall?
The length of a 12-foot by 8-foot rectangle is increasing at a rate of 3 feet per second and the width is decreasing at 2 feet per second:
1. How fast is the perimeter changing?
2. How fast is the area changing?
A circle of radius 3 inches is inside a square with 12-inch sides:
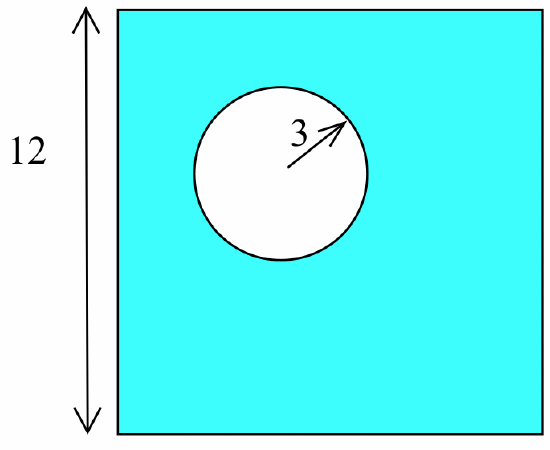
$The interior of a black sqaure is shaded light blue. A double arrow denoting the height of the square is labeled '12.' The radius of a disk cut out of the interior of the square has a radius indicated by an arrow that is labeled '3.'$
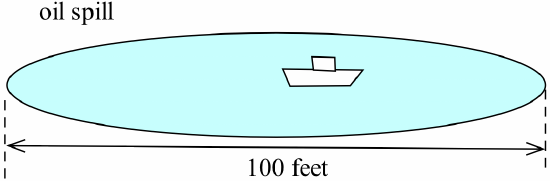
How fast is the area between the circle and square changing if the radius is increasing at 4 inches per minute and the sides are increasing at 2 inches per minute?
An oil tanker in Puget Sound has sprung a leak, and a circular oil slick is forming. The oil slick is 4 inches thick everywhere, is 100 feet in diameter, and the diameter is increasing at 12 feet per hour. Your job, as the Coast Guard commander or the tanker’s captain, is to determine how fast the oil is leaking from the tanker.
$A light blue oval shape labeled 'oil spill' representes a side view of a circular region, in the middle of which are two trapezoids representing a ship. A double arrow denotes the diameter of the circular region, labeled '100 feet.'$
A mathematical species of slug has a semicircular cross section and is always 5 times as long as it is high:

When the slug is 5 inches long, it is growing at 0.2 inches per week.
1. How fast is its volume increasing?
2. How fast is the area of its “foot” (the part of the slug in contact with the ground) increasing?
Lava flowing from a hole at the top of a hill is forming a conical mountain whose height is always the same as the width of its base:
$A red isoceles triangle with black curve segements at the top vertex is labeled 'volcano.' The height (labeled 'h') and the base (labeled 'w=h') are denoted by double arrows.$
If the mountain is increasing in height at 2 feet per hour when it is 500 feet high, how fast is the lava flowing (that is, how fast is the volume of the mountain increasing)? ($V = \frac13 \pi r^2 h$)
A 6-foot-tall person is walking away from a 14-foot lamp post at 3 feet per second.

When the person is 10 feet away from the lamp post:
1. how fast is the length of the shadow changing?
2. how fast is the tip of the shadow moving away from the lamp post?
Redo the previous problem if the person is 20 feet from the lamp post.
Water is being poured at a rate of 15 cubic feet per minute into a conical reservoir that is 20 feet deep and has a top radius of 10 feet:
1. How long will it take to fill the empty reservoir?
2. How fast is the water level rising when the water is 4 feet deep?
3. How fast is the water level rising when the water is 16 feet deep?
The string of a kite is perfectly taut and always makes an angle of $35^\circ$ above horizontal.
1. If the kite flyer has let out 500 feet of string, how high is the kite?
2. If the string is let out at a rate of 10 feet per second, how fast is the kite's height increasing?
A small tracking telescope is viewing a hot-air balloon rise from a point 1,000 meters away from a point directly under the balloon.
1. When the viewing angle is $20^\circ$, it is increasing at a rate of $3^{\circ}$ per minute. How high is the balloon, and how fast is it rising?
2. When the viewing angle is $80^{\circ}$, it is increasing at a rate of $2^{\circ}$ per minute. How high is the balloon, and how fast is it rising?
The 8-foot diameter of a spherical gas bubble is increasing at 2 feet per hour, and the 12-foot-long edges of a cube containing the bubble are increasing at 3 feet per hour. Is the volume contained between the spherical bubble and the cube increasing or decreasing? At what rate?
In general, the strength $S$ of an animal is proportional to the cross-sectional area of its muscles, and this area is proportional to the square of its height $H$, so the strength $S = aH^2$. Similarly, the weight $W$ of the animal is proportional to the cube of its height, so $W = bH^3$. Finally, the relative strength $R$ of an animal is the ratio of its strength to its weight. As the animal grows, show that its strength and weight increase, but that the relative strength decreases.
The snow in a hemispherical pile melts at a rate proportional to its exposed surface area (the surface area of the hemisphere). Show that the height of the snow pile is decreasing at a constant rate.
If the rate at which water vapor condenses onto a spherical raindrop is proportional to the surface area of the raindrop, show that the radius of the raindrop will increase at a constant rate.
Define $A(x)$ to be the area bounded by the $t$- and $y$-axes, and the lines $y = 5$ and $t = x$.
1. Find a formula for $A$ as a function of $x$.
2. Determine $A'(x)$ when $x = 1$, $2$, $4$ and $9$.
3. If $x$ is a function of time, $x(t) = t^2$, find a formula for $A$ as a function of $t$.
4. Determine $A'(t)$ when $t = 1$, $2$ and $3$.
5. Suppose instead $x(t) = 2 + \sin(t)$. Find a formula for $A(t)$ and determine $A'(t)$.
The point $P$ is going around the circle $x^2 + y^2 = 1$ twice a minute.

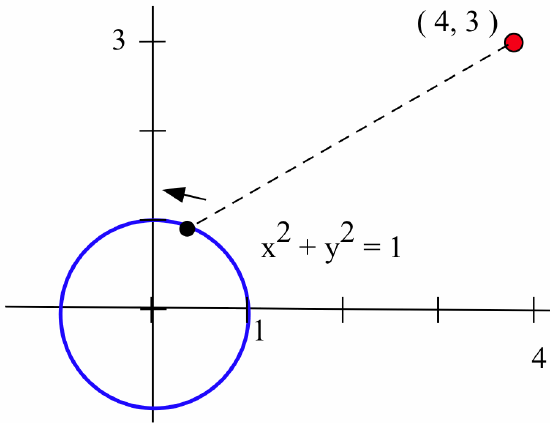
How fast is the distance between the point $P$ and the point $(4,3)$ changing:
1. when $P = (1,0)$?
2. when $P = (0,1)$?
3. when $P = (0.8,0.6)$?
(Suggestion: Write $x$ and $y$ as parametric functions of time $t$.)
You are walking along a sidewalk toward a 40-foot-wide sign adjacent to the sidewalk and perpendicular to it.

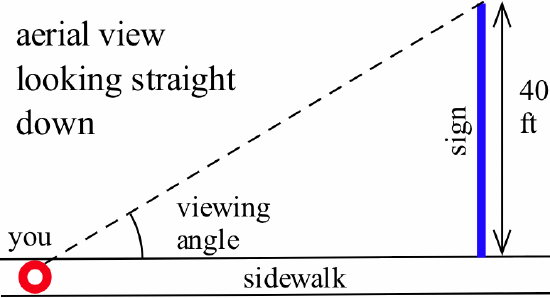
If your viewing angle $\theta$ is $10^{\circ}$:
1. how far are you from the corner of the sign?
2. how fast is your viewing angle changing if you are walking at 25 feet per minute?
3. how fast are you walking if the angle is increasing at $2^{\circ}$ per minute?