2.A: Answers
- Page ID
- 212020
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Section 2.0
- Values are approximate; your answers may vary.
\(x\) \(f(x)\) \(m(x)\) \(x\) \(f(x)\) \(m(x)\) \(0.0\) \(1.0\) \(1\) \(2.5\) \(0.0\) \(-2\) \(0.5\) \(1.4\) \(\frac12\) \(3.0\) \(-1.0\) \(-2\) \(1.0\) \(1.6\) \(0\) \(3.5\) \(-1.3\) \(0\) \(1.5\) \(1.4\) \(-\frac12\) \(4.0\) \(-1.0\) \(1\) \(2.0\) \(1.0\) \(-2\) -
- At \(x = 1\), \(3\) and \(4\).
- Largest at \(x = 4\); smallest at \(x = 3\).
![A blue curve graphed on a [0,5]X[-1,4] grid, starting at (0,1) and moving linearly to (0.6,1), then dipping steeply through (1,0) before flattening near (1.2,-1.2) and reaching a minimum a (1.8,-2.), then rising through (2.9,0) to a maximum near (3.5,4) before descenging toward (4.5,-1), where it flattens out.](https://math.libretexts.org/@api/deki/files/140298/ans200_3.png?revision=1)
-
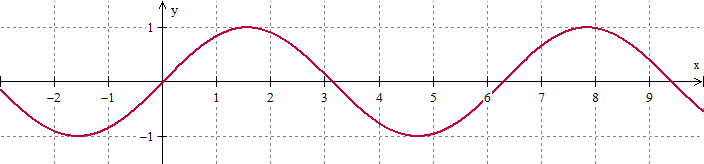

- \(m(x) = \cos(x)\)
- Assume we turn off the engine at the point \((p,q)\) on the curve \(y = x^2\) and then find values of \(p\) and \(q\) so the tangent line to \(y = x^2\) at the point \((p,q)\) goes through the given point \((5,16)\): \((p,q)\) is on \(y = x^2\) so \(q = p^2\) and %an equation of the tangent line to \(y = x^2\) at \((p, p^2)\) is \(y = 2px - p^2\) so, substituting \(x = 5\) and \(y = 16\), we have \(16 = 2p(5)-p^2 \Rightarrow p^2 - 10p + 16 = 0 \Rightarrow p = 2\) or \(p = 8\). The solution we want (moving left to right along the curve) is \(p = 2\), \(q = p^2 = 4\) (\(p = 8\), \(q = 64\) would be the right-to-left solution).
- Impossible: \((1, 3)\) sits “inside” the parabola.
-
- \(\displaystyle m_{\mbox{sec}} = \frac{f(x+h) - f(x)}{(x+h) - x} = \frac{\left[3(x + h) - 7 \right] - \left[ 3x - 7 \right]}{(x + h) - x} = \frac{3h}{h} = 3\)
- \(\displaystyle m_{\mbox{tan}} = \lim_{h\to 0}\, m_{\mbox{sec}} = \lim_{h\to 0}\, 3 = 3\).
- At \(x = 2\), \(m_{\mbox{tan}} = 3\).
- \(f(2) = -1\) so the tangent line is \(y - (-1) = 3(x - 2)\) or \(y = 3x -7\).
-
- \(\displaystyle m_{\mbox{sec}} = \frac{\left[ a(x + h) + b \right] - \left[ ax + b\right]}{(x + h) - x} = \frac{ah}{h} = a\)
- \(\displaystyle m_{\mbox{tan}} = \lim_{h\to 0}\, m_{\mbox{sec}} = \lim_{h\to 0}\, a = a\).
- At \(x = 2\), \(m_{\mbox{tan}} = a\).
- \(f(2) = 2a+b\) so the tangent line is \(y - (2a + b) = a(x - 2)\) or \(y = ax + b\).
-
- \(m_{\mbox{sec}} = \frac{\left[ 8 - 3(x + h)^2 \right] - \left[ 8 - 3x^2\right]}{(x + h) - x} = -6x-3h\)
- \(\displaystyle m_{\mbox{tan}} = \lim_{h\to 0}\, m_{\mbox{sec}} = \lim_{h\to 0}\, \left[-6x-3h\right] = -6x\).
- At \(x = 2\), \(m_{\mbox{tan}} = -6(2) = -12\)
- \(f(2) = -4\) so the tangent line is \(y - (-4) = -12(x - 2)\) or \(y = -12x + 20\).
- \(a = 1\), \(b = 2\), \(c = 0 \Rightarrow m_{\mbox{tan}} = (2)(1)(x) + 2 = 2x + 2\) so we need \(p\) to satisfy \(6 - (p^2+ 2p) = (2p + 2)(3 - p) \Rightarrow p^2 - 6p = 0\) \(\Rightarrow p = 0\) or \(p = 6\) so the points are \((0, 0)\) and \((6, 48)\).
Section 2.1
- derivative
- of \(g\)
- of \(h\)
- of \(f\)
-
- \(\displaystyle m_{\mbox{sec}} = h - 4 \Rightarrow m_{\mbox{tan}} = \lim_{h\to 0}\, m_{\mbox{sec}} = -4\)
- \(\displaystyle m_{\mbox{sec}} = h + 1 \Rightarrow m_{\mbox{tan}} = \lim_{h\to 0}\, m_{\mbox{sec}} = 1\)
-
- \(\displaystyle m_{\mbox{sec}} = 5-h \Rightarrow m_{\mbox{tan}} = \lim_{h\to 0}\, m_{\mbox{sec}} = 5\)
- \(\displaystyle m_{\mbox{sec}} = 7-2x-h \Rightarrow m_{\mbox{tan}} = 7-2x\)
-
- \(-1\)
- \(-1\)
- \(0\)
- \(+1\)
- DNE
- DNE
- Using the definition: \begin{align*} f'(x) &= \lim_{h\to 0}\, \frac{\left[(x + h)^2 +8\right]-\left[ x^2 +8\right]}{h}\\ &= \lim_{h\to 0}\, \frac{2xh + h^2}{h} = \lim_{h\to 0}\, \left[2x + h\right] = 2x\end{align*} so \(f'(3)= 2\cdot 3 = 6\)
- Using the definition: \begin{align*} f'(x) &= \lim_{h\to 0}\, \frac{\left[2(x + h)^3 - 5(x + h)\right]-\left[ 2x^3-5x\right]}{h}\\ &= \lim_{h\to 0}\, \frac{6x^2h +6xh^2 +2h^3 - 5h}{h}\\ &= \lim_{h\to 0}\, \left[6x^2+6xh+2h^2-5\right] = 6x^2-5\end{align*} so \(f'(3)= 6\cdot 3^2-5 = 49\)
- For any constant \(C\), if \(f(x) = x^2 + C\), then: \begin{align*} f'(x) &= \lim_{h\to 0}\, \frac{f(x + h)- f(x)}{h}\\ &= \lim_{h\to 0}\, \frac{\left[(x + h)^2 + C\right] - \left[ x^2 +C\right]}{h}\\ &= \lim_{h\to 0}\, \frac{2xh + h^2}{h} = \lim_{h\to 0}\, \left[2x + h\right] = 2x \end{align*} The graphs of \(f(x) = x^2\), \(g(x) = x^2 + 3\) and \(h(x) = x^2 - 5\) are “parallel” parabolas: \(g\) is \(f\) shifted up 3 units; \(h\) is \(f\) shifted down 5 units.
- \(f'(x) = 2x \Rightarrow f'(1) = 2\) so an equation of the tangent line at \((1,9)\) is \(y - 9 = 2(x - 1)\) or \(y = 2x + 7\); \(f'(-2) = -4\) so an equation of the tangent line at \((-2,12)\) is \(y - 12 = -4(x + 2)\) or \(y = -4x + 4\).
- \(f'(x) = \cos(x) \Rightarrow f'(\pi) = \cos(\pi) = -1\) so an equation of the tangent line at \((\pi,0)\) is \(y - 0 = -1(x - \pi)\) or \(y = -x + \pi\); \(f'\left(\frac{\pi}{2}\right) = \cos\left(\frac{\pi}{2}\right) = 0\) so an equation of the tangent line at \(\left(\frac{\pi}{2},1\right)\) is \(y - 1 = 0\left(x - \frac{\pi}{2}\right)\) or \(y = 1\).
-
- \(y - 5 = 4(x - 2)\) or \(y = 4x - 3\)
- \(x + 4y = 22\) or \(y = -0.25x + 5.5\)
- \(f'(x) = 2x\), so the tangent line is horizontal only if \(x = 0\): at the point \((0,1)\).
- \(f'(p) = 2p\) (the slope of the tangent line) so \(y - q = 2p(x - p)\) or \(y = 2px + (q - 2p^2)\). Since \(q = p^2 + 1\), the tangent line is \(y = 2px + (p^2 + 1 - 2p^2) = 2px - p^2 + 1\).
- We need \(p\) such that \(-7 = 2p(1) - p^2 + 1\), so \(p^2 - 2p - 8 = 0 \Rightarrow p = -2\) or \(p=4\). There are two such points: \((-2, 5)\) and \((4, 17)\).
-
- \(y'(x) = 2x\), so \(y'(1) = 2\) and the angle is \(\arctan(2) \approx 1.107\) radians \(\approx 63^{\circ}\)
- \(y'(x) = 3x^2\) so \(y'(1) = 3\) and the angle is \(\arctan(3) \approx 1.249\) radians \(\approx 72^{\circ}\)
- \(1.249 - 1.107\) radians = \(0.142\) radians (or \(71.57^{\circ} - 63.43^{\circ} \approx 8.1^{\circ}\))
- Units on the horizontal axis are “seconds”; units on the vertical axis are “feet per second.”
![A blue curve graphed on a [0,6.5]X[-20,10] grid that begins on the horizontal axis before dipping near x = 0.2 toward a minimum at (1,-19), the rising symmetrically to (2,0), where it is horizontal to (3.5,0), then rises in a concave-down shape to a maximum at (4,10), then falls to (4.6,0), where it becomes concave up and falls to a low point at (5.2,-12), then stays horizontal past x = 6.5.](https://math.libretexts.org/@api/deki/files/140302/ans201_23.png?revision=1)
-
- \(d(4) = 256\) ft; \(d(5) = 400\) ft
- \(d'(x) = 32x \Rightarrow d'(4) = 128\) ft/sec and \(d'(5) = 160\) ft/sec.
- Marginal production cost is \(C'(x) = \frac{1}{2\sqrt{x}}\) dollars per golf ball, so \(C'(25) = \frac{1}{2\sqrt{25}} = \frac{1}{10} = 0.10\) per ball and \(C'(100) = \frac{1}{2\sqrt{100}} = \frac{1}{20} = 0.05\) per ball.
-
- \(A(0) = 0\), \(A(1) = \frac12\), \(A(2) = 2\) and \(A(3) = \frac92\).
- \(\displaystyle A(x) = \frac{x^2}{2}\) (\(x \geq 0\))
- \(A'(x) = x\)
- \(A'(x)\) represents the rate at which \(A(x)\) is increasing (the rate at which area is accumulating).
-
- \(9x^8\)
- \(\displaystyle \frac{2}{3x^{\frac13}}\)
- \(\displaystyle \frac{-4}{x^5}\)
- \(\pi x^{\pi - 1}\)
- \(1\) if \(x > -5\) and \(-1\) if \(x < -5\)
- \(f(x) = x^3 + 4x^2\) (plus any constant)
- \(f(t) = 5\cdot\sin(t)\)
- \(f(x) = \frac12 x^2 + \frac13 x^3\)
Section 2.2
-
- \(0\), \(1\), \(2\), \(3\), \(5\)
- \(0\), \(3\), \(5\)
- In the table below, und. means “undefined”:
\(x\) \(f(x)\cdot g(x)\) \(( f(x)\cdot g(x))'\) \(\frac{f(x)}{g(x)}\) \(\left( \frac{f(x)}{g(x)} \right)'\) \(0\) \(2\) \(13\) \(2\) \(-7\) \(1\) \(-15\) \(16\) \(-\frac35\) \(\frac{4}{25}\) \(2\) \(0\) \(-6\) \(0\) \(-\frac32\) \(3\) \(0\) \(3\) und. und. -
\(x\) \(f+g\) \((f+g)'\) \(f\cdot g\) \(\left(f\cdot g\right)'\) \(\frac{f}{g}\) \(\left(\frac{f}{g}\right)'\) \(1\) \(5\) \(0\) \(6\) \(2\) \(\frac32\) \(-\frac{10}{4}\) \(2\) \(4\) \(\frac12\) \(3\) \(\frac12\) \(\frac13\) \(-\frac{1}{18}\) \(3\) \(4\) \(0\) \(4\) \(0\) \(1\) \(1\) -
- \(\mbox{D}\left( (x-5)(3x+7) \right) = (x-5)\cdot3 + (3x+7)\cdot1\)
- \(\mbox{D}\left( 3x^2 - 8x - 35 \right) = 6x - 8\) (the same result)
- \(19\cdot 3x^2 = 57x^2\)
- \(\cos(x)-\sin(x)\)
- \(x^2\cdot\left[-\sin(x)\right]+\cos(x)\cdot 2x\)
- Applying the Product Rule: \begin{align*}\mbox{D}\left(\sin^2(x)\right) &= \sin(x)\cdot \cos(x) + \sin(x)\cdot\cos(x)\\ &= 2\sin(x)\cos(x) = \sin(2x)\end{align*}
- \(\displaystyle \frac{d}{dx} \left(\frac{\cos(x)}{x^2}\right) = \frac{x^2\left(-\sin(x)\right) - \left(\cos(x) \right)( 2x )}{\left(x^2\right)^2} = \frac{-x\left[x\sin(x) + 2\cos(x)\right]}{x^4} = -\frac{x\sin(x) + 2\cos(x)}{x^3}\)
- \(\displaystyle \frac{(1+x^2)\cdot 0 - 1\cdot 2x}{\left(1+x^2\right)^2} = -\frac{2x}{\left(1+x^2\right)^2}\)
- \(\displaystyle \frac{\cos(\theta)\cdot 0 - 1\cdot \left(-\sin(\theta)\right)}{\left(\cos(\theta)\right)^2} = \frac{\sin(\theta)}{\cos^2(\theta)}\)
- \(\displaystyle \frac{\cos(\theta)\cdot \cos(\theta) - \sin(\theta)\cdot \left(-\sin(\theta)\right)}{\left(\cos(\theta)\right)^2} = \frac{1}{\cos^2(\theta)}\)
- \(40x^4-12x^3+6x^2+14x-12\)
- \(f(x) = ax^2 + bx+ c\) so \(f(0) = c\), hence \(f(0) = 0\) \(\Rightarrow c = 0\). \(f'(x) = 2ax + b\) so \(f'(0) = b\), hence \(f'(0) = 0 \Rightarrow b = 0\). Finally, \(f'(10) = 20a + b = 20a\) so \(f'(10) = 30 \Rightarrow 20a = 30 \Rightarrow a = \frac32 \Rightarrow f(x) = \frac32 x^2 + 0x + 0 = \frac32 x^2\).
- Their graphs are vertical shifts of each other, and their derivatives are equal.
- \(f(x)\cdot g(x) = k \Rightarrow \mbox{D}\left(f(x)\cdot g(x) \right) = \mbox{D}\left( k \right) = 0\) so \(f(x)\cdot g'(x) + g(x)\cdot f'(x) = 0\). If \(f(x) \neq 0\) and \(g(x) \neq 0\), then \(\frac{f'(x)}{f(x)} = -\frac{g'(x)}{g(x)}\).
-
- \(f'(x) = 2x - 5\), so \(f'(1) = -3\)
- \(f'(x) = 0\) only if \(x = \frac52\).
-
- \(f'(x) = 3 + 2\sin(x)\); \(f'(1) = 3 + 2\sin(1) \approx 4.7\)
- \(f'(x)>0\) because \(\sin(x) > -\frac32\) for all \(x\).
-
- \(f'(x) = 3x^2 + 18x = 3x(x + 6)\), so \(f'(1) = 21\)
- \(f'(x) = 0\) only if \(x = 0\) or \(x = -6\).
-
- \(f'(x) = 3x^2 + 4x + 2\), so \(f'(1) = 9\)
- \(f'(x) > 0\) (the discriminant \(4^2 - 4(3)(2) < 0\)).
-
- \(f'(x) = x\cos(x) + \sin(x) \Rightarrow f'(1) = \cos(1) + \sin(1) \approx 1.38\)
- The graph of \(f'(x)\) crosses the \(x\)-axis infinitely often. The root of \(f'\) at \(x = 0\) is easy to see; approximate others, such as those near \(x = 2.03\) and \(4.91\) and \(-2.03\), using technology.
- \(f'(x) = 3x^2 + 2Ax + B\): the graph of \(y = f(x)\) has two distinct “vertices” if \(f'(x) = 0\) for two distinct values of \(x\). This occurs if the discriminant of \(3x^2 + 2Ax + B > 0\): \((2A)^2 - 4(3)(B) > 0\).
- Everywhere except at \(x = (2k+1)\frac{\pi}{2}\).
- Everywhere except at \(x = 0\) and \(x = 3\).
- Everywhere except at \(x = 1\).
- Everywhere. The only possible difficulty is at \(x = 0\): the definition of the derivative gives \(f'(0) = 1\) and the derivatives of the “two pieces” of \(f\) match (and equal \(1\)) at \(x = 0\).
- Continuity of \(f\) at \(x = 1\) requires \(A + B = 2\). The “left derivative” of \(f\) at \(x = 1\) is \(\mbox{D}( Ax + B ) = A\) and the “right derivative” of \(f\) at \(x = 1\) is \(3\) (if \(x > 1\) then \(\mbox{D}( x^2 + x ) = 2x + 1\)), so to achieve differentiability we need \(A = 3\) and \(B = 2 - A = -1\).
-
- \(h(x) = 128x - 2.65x^2 \Rightarrow h'(x) = 128 - 5.3x\) so \(h'(0) = 128\) ft/sec, \(h'(1) = 122.7\) ft/sec and \(h'(2) = 117.4\) ft/sec
- \(v(x) = h'(x) = 128 - 5.3x\) ft/sec
- \(v(x) = 0\) when \(x = \frac{128}{5.3} \approx 24.15\) sec
- \(h(24.15) \approx 1545.66\) ft
- about 48.3 seconds: 24.15 up and 24.15 down
-
- \(h(x) = v_o x - 16x^2 \Rightarrow h'(x) = v_o - 32x\) ft/sec
- Max height when \(x = \frac{v_o}{32}\): max height \(= h\left(\frac{v_o}{32}\right) = v_o\left(\frac{v_o}{32}\right) - 16\left(\frac{v_o}{32}\right)^2 = \frac{(vo)^2}{64}\) ft
- Time aloft \(= 2\left(\frac{v_o}{32}\right) = \frac{v_o}{16}\) sec
-
- \(\frac{(v_o)^2}{64} = 3.75 \Rightarrow v_o = 8\sqrt{3.75} \approx 15.5\) ft/sec
- \(2\left(\frac{v_o}{32}\right) = \frac{8\sqrt{3.75}}{16} \approx 0.97\) sec
- Max lift \(= \frac{(v_o)^2}{2g} = \frac{( 8\sqrt{3.75})^2}{2(5.3)} = \frac{240}{10.6} \approx 22.64\) ft
-
- \(y' = -\frac{1}{x^2}\) so \(y'(2) = -\frac14\) and the tangent line is \(y - 1/2 = (-\frac14)(x - 2)\) or \(y = -\frac14 x + 1\)
- \(x\)-intercept at \((4,0)\); \(y\)-intercept at \((0,1)\)
- \(A = \frac12 (\mbox{base})(\mbox{height}) = \frac12(4)(1) = 2\)
- Because \((1,4)\) and \((3,14)\) are on the parabola, we need \(a + b + c = 4\) and \(9a + 3b + c = 14\). Subtracting the first equation from the second, \(8a + 2b = 10\); \(f'(x) = 2ax + b\) so \(f'(3) = 6a + b = 9\), the slope of \(y = 9x - 13\). Now solve the system \(8a + 2b = 10\) and \(6a + b = 9\) to get \(a = 2\) and \(b = -3\). Then use \(a + b + c = 4\) to get \(c = 5\): \(a = 2\), \(b = -3\), \(c = 5\).
-
- \(f(x) = x^3\)
- \(g(x) = x^3 + 1\)
- If \(h(x) = x^3 + C\) for any constant \(C\), then \(\mbox{D}\left(h(x)\right) = 3x^2\).
-
- For \(0 \leq x \leq 1\), \(f'(x) = 1\) so \(f(x) = x + C\); because \(f(0) = 0\), we know \(C = 0\) and \(f(x) = x\). For \(1 \leq x \leq 3\), \(f'(x) = 2 - x\) so \(f(x) = 2x - \frac12 x^2 + K\); because \(f(1) = 1\), we know \(K = -\frac12\) and \(f(x) = 2x - \frac12 x^2 - \frac12\). For \(3 \leq x \leq 4\), \(f'(x) = x - 4\) so \(f(x) = \frac12x^2- 4x + L\); because \(f(3) = 1\), we know \(L = \frac{17}{2}\) and \(f(x) = \frac12 x^2 - 4x +\frac{17}{2}\).
- A vertical shift, up 1 unit, of the graph in (a).
Section 2.3
- \(\mbox{D}(f^2(x)) = 2\cdot f^1(x)\cdot f'(x)\); at \(x = 1\), \(\mbox{D}(f^2(x)) = 2(2)(3) = 12\). \(\mbox{D}(f^5(x)) = 5\cdot f^4(x)\cdot f'(x)\); at \(x = 1\), \(\mbox{D}(f^5(x)) = 5(2^4)(3) = 240\). \(\mbox{D}(f^{\frac12}(x)) = \frac12 \cdot f^{-\frac12}(x)\cdot f'(x)\); at \(x = 1\), \(\mbox{D}(f^{\frac12}(x)) = (\frac12)(2^{-\frac12})(3)\) \(= \frac{3}{2\sqrt{2}} = \frac{3\sqrt{2}}{4}\).
-
\(x\) \(f(x)\) \(f'(x)\) \(\mbox{D}(f^2)\) \(\mbox{D}(f^3)\) \(\mbox{D}(f^5)\) \(1\) \(1\) \(-1\) \(-2\) \(-3\) \(-5\) \(3\) \(2\) \(-3\) \(-12\) \(-36\) \(-240\) - \(f'(x) = 5\cdot (2x - 8)^4 \cdot (2) = 10(2x - 8)^4\)
- \(f'(x) = x\cdot 5\cdot (3x + 7)^4 \cdot 3 + 1\cdot(3x + 7)^5 = (3x + 7)^4 \left[ 15x + (3x + 7) \right] = (3x + 7)^4( 18x + 7)\)
- \(\displaystyle f'(x) = \frac12 (x^2 + 6x - 1)^{-\frac12}\cdot(2x + 6)\), which we can rewrite as \(\displaystyle \frac{x + 3}{\sqrt{x^2 + 6x - 1}}\)
-
- Graph of \(h(t) = 3-2\sin(t)\):
![A red graph of 3-2\sin(t) on a [0,9.5]X[0,5.5] grid.](https://math.libretexts.org/@api/deki/files/140297/ans203_11.png?revision=1&size=bestfit&width=353&height=209)
- When \(t = 0\), \(h(0) = 3\) feet.
- highest: 5 feet above the floor; lowest: 1 foot above the floor.
- \(v(t) = h'(t) = -2\cos(t)\) ft/sec, \(a(t) = v'(t) = 2\sin(t)\) ft/sec\(^2\).
- This spring oscillates forever. The motion of a real spring would “damp out” due to friction.
- Graph of \(h(t) = 3-2\sin(t)\):
-
- If \(h(t) = 5t\), then \(v(t) = h'(t) = 5\) and \(K(1) = K(2) = \frac12 m(5^2) = 12.5m\).
- If \(h(t) = t^2\), then \(v(t) = h'(t) = 2t\) so \(v(1) = 2\) and \(v(2) = 4\), hence \(K(1) = \frac12 m(2^2) = 2m\) and \(K(2) = \frac12 m(4^2) = 8m\).
- \(x\cdot(\sin(x))' + \sin(x)\cdot(x)' = x\cos(x) + \sin(x)\)
- \(f'(x) = e^x - \sec(x)\cdot\tan(x)\)
- \(f'(x) = -e^{-x} + \cos(x)\)
- \(f'(x) = 7(x - 5)^6(1)\) so \(f'(4) = 7(-1)^6(1) = 7\). Tangent line: \(y - (-1) = 7(x - 4)\) or \(y = 7x - 29\).
- \(f'(x) = \frac12 (25 - x^2)^{-\frac12}(-2x) = \frac{-x}{\sqrt{25 - x^2}}\) so \(f'(3) = \frac{-3}{\sqrt{25-9}} = -\frac34\). Tangent line: \(y - 4 = -\frac34 (x - 3)\) or \(3x + 4y = 25\).
- \(f'(x) = 5(x - a)^4 (1)\) so \(f'(a) = 5(a - a)^4(1) = 0\). Tangent line: \(y - 0 = 0(x - a)\) or \(y = 0\).
-
- \(f'(x) = e^x\) so \(f'(3) = e^3\). Tangent line: \(y - e^3 = e^3 (x - 3)\) or \(y = e^3 x -2e^3\).
- \(0 - e^3 = e^3 (x - 3) \Rightarrow -1 = x - 3 \Rightarrow x = 2\)
- \(f'(p) = e^p\) so tangent line at \((p, e^p)\) is \(y - e^p = e^p (x - p)\); \(x\)-intercept: \(0 - e^p = e^p (x - p) \Rightarrow -1 = x - p \Rightarrow x = p - 1\)
- \(f'(x) = -\sin(x) \Rightarrow f''(x) = -\cos(x)\)
- \(f'(x) = x^2 \cos(x) + 2x \sin(x) \Rightarrow f''(x) = -x^2 \sin(x) + 2x \cos(x) + 2x \cos(x) + 2 \sin(x) = -x^2 \sin(x) + 4x \cos(x) + 2\sin(x)\)
- \(f'(x) = e^x \cos(x) - e^x \sin(x) \Rightarrow f''(x) = -2e^x\sin(x)\)
- \(q' =\) linear, \(q'' =\) constant, \(q''' = q^{(4)} = \cdots = 0\)
- \(p^{(n)} =\) constant \(\Rightarrow p^{(n+1)} = 0\)
- \(f(x) = 5e^x\)
- \(f(x) = (1 + e^x)^5\)
- No. Using the definition of the derivative:\[\lim_{h\to 0}\, \frac{f(0+ h) - f(0)}{h} = \lim_{h\to 0}\, \frac{(0+ h)\cdot\sin\left(\frac{1}{0+ h}\right) - 0}{h}\nonumber\]which simplifies to \(\displaystyle \lim_{h\to 0}\, \sin\left(\frac{1}{h}\right)\); to see that this last limit does not exist, graph \(\sin\left(\frac{1}{h}\right)\) or evaluate \(\sin\left(\frac{1}{h}\right)\) for small values of \(h\).
- \(\displaystyle \left(1 + \frac{1}{x}\right)^x \approx 2.718\ldots = e\) when \(x\) is large.
-
- \(s_2 = 2.5\), \(s_3 \approx 2.67\), \(s_4 \approx 2.708\), \(s_5 \approx 2.716\), \(s_6 \approx 2.718\), \(s_7 \approx 2.71825\), \(s8 \approx 2.718178\)
- They are approaching \(e\).
Section 2.4
- \(f(x) = x^5\), \(g(x) = x^3 - 7x \Rightarrow f\circ g(x) = (x^3 - 7x)^5\)
- Setting \(f(x) = x^{\frac52}\) and \(g(x) = 2 + \sin(x)\) yields \(f\circ g(x) = (2 +\sin(x))^{\frac52}\). (The functions \(f(x) = \sqrt{x}\) and \(g(x) = (2 + \sin(x))^5\) also work.)
- \(f(x) = \left| x \right|\), \(g(x) = x^2 - 4 \Rightarrow f\circ g(x) = \left| x^2 - 4 \right|\)
- \(y = u^5\), \(u = x^3 - 7x\); \(y = u^4\), \(u = \sin(3x - 8)\); \(y = u^{\frac52}\), \(u = 2 + \sin(x)\); \(y = \frac{1}{\sqrt{u}}\), \(u = x^2 + 9\); \(y = \left| u \right|\), \(u = x^2 - 4\); \(y = \tan(u)\), \(u = \sqrt{x}\)
-
\(x\) \(f \circ g(x)\) \((f \circ g)'(x)\) \(-2\) \(1\) \(0\) \(-1\) \(1\) \(2\) \(0\) \(0\) \(1\) \(1\) \(2\) \(2\) \(2\) \(-2\) \(-2\) - \(g(2) \approx 2\), \(g'(2) \approx -1\), \((f\circ g)(2) = f( g(2) ) \approx f( 2 ) \approx 1, f'( g(2) ) \approx f '( 2 ) \approx 0\), \((f\circ g)'(2) = f'( g(2))\cdot g'(2) \approx 0\)
- \(\mbox{D}\left( \left( 1 - \frac{3}{x}\right)^4\right) = 4\left(1 - \frac{3}{x})\right)^3 \cdot\frac{3}{x^2}\)
- \(5\left(-\frac12\right)\left(2 + \sin(x)\right)^{-\frac32}\cdot \cos(x) = \frac{-5 \cos(x)}{2(2 + \sin(x))^{\frac32}}\)
- \(x^2\cdot\left[\cos(x^2 + 3) \cdot 2x\right] + \sin(x^2 + 3) \cdot 2x = 2x\left[x^2 \cos(x^2 + 3) + \sin(x^2 + 3)\right]\)
- \(\frac{7}{\cos(x^3 - x)} = 7\sec\left(x^3 - x\right)\) so \(\mbox{D}\left( 7\sec\left(x^3 - x\right)\right) = 7(3x^2 -1)\cdot \sec(x^3 - x).\tan(x^3 - x)\)
- \(\mbox{D}\left(e^x + e^{-x}\right) = e^x - e^{-x}\)
-
- \(h(0) = 2\) feet above the floor.
- \(h(t) = 3 - \cos(2t)\) ft, \(v(t) = h'(t) = 2\sin(2t)\) ft/sec, \(a(t) = v'(t) = 4\cos(2t)\) ft/sec\(^2\)
- \(K = \frac12 mv^2 = \frac12 m\left(2\sin(2t)\right)^2 = 2m\sin^2(2t)\), \(\frac{dK}{dt} = 8m\cdot\sin(2t)\cdot\cos(2t)\)
-
- \(P(0) = 14.7\) psi (pounds per square inch), \(P(30000) \approx 4.63\) psi
- \(10 = 14.7 e^{-0.0000385h} \Rightarrow \frac{10}{14.7} = e^{-0.0000385h} \Rightarrow h = \frac{1}{-0.0000385}\ln\left(\frac{10}{14.7}\right) \approx\) 10,007 ft
- \(\frac{dP}{dh} = 14.7(-0.0000385)e^{-0.0000385h}\) psi/ft. At \(h =\) 2,000 ft, \(\frac{dP}{dh} = 14.7(-0.0000385)e^{-0.0000385(2000)}\) psi/ft \(\approx -0.000524\) psi/ft. Finally, \(\frac{dP}{dt} = 500(-0.000524) \approx -0.262\) psi/min.
- If temperature is constant, then (from physics!) we know (pressure)(volume) is constant, so decreasing pressure means increasing volume.
- \(\displaystyle \frac{2\cos(z)\left[-\sin(z)\right]}{2\sqrt{1 + \cos^2(z)}} = \frac{-\sin(2z)}{2\sqrt{1 + \cos^2(z)}}\)
- \(\frac{d}{dx} \tan(3x + 5) = 3\cdot \sec^2(3x + 5)\)
- \(\mbox{D}\left(\sin(\sqrt{x + 1})\right) = \cos\left(\sqrt{x + 1}\right)\cdot\frac{1}{2\sqrt{x + 1}}\)
- \(\displaystyle \frac{d}{dx}\left(e^{\sin(x)}\right) = e^{\sin(x)}\cdot\cos(x)\)
- \(f(x) = \sqrt{x} \Rightarrow f'(x) = \frac{1}{2\sqrt{x}}\); \(x(t) = 2 + \frac{21}{t} \Rightarrow x'(t) = -\frac{21}{t^2}\). At \(t = 3\), \(x = 9\) and \(x'(t) = -\frac{21}{9} = -\frac{7}{3}\) so \(\frac{d}{dt}\left(f(x(t))\right) = \left(\frac{1}{2\sqrt{9}}\right)\left(-\frac73\right) = - \frac{7}{18}\).
- \(f(x) = \tan^3(x) \Rightarrow f'(x) = 3\cdot \tan^2(x)\cdot \sec^2(x)\); \(x(t) = 8 \Rightarrow x'(t) = 0\). When \(t = 3\), \(x = 8\) and \(x'(t) = 0\) so \(\frac{d}{dt} \left(f(x(t))\right) = 0\).
- \(f(x) = \frac{1}{77}(7x - 13)^{11}\)
- \(f(x) = - \frac12\cos(2x - 3)\)
- \(f(x) = e^{\sin(x)}\)
- \(-2\sin(2x) = 2\cos(x)\left[-\sin(x)\right] - 2\sin(x)\cdot\cos(x)\) or \(\sin(2x) = 2\sin(x)\cdot \cos(x)\)
- \(3\cos(3x) = 3\cos(x) - 12\sin^2(x)\cdot\cos(x)\) so \(\cos(3x) =\cos(x)\left[1 - 4\sin^2(x)\right] = \cos(x)\left[1 - 4 + 4\cos^2(x)\right]\) \(= 4\cos^3(x) - 3\cos(x)\)
- \(y' = 3Ax^2 + 2Bx\)
- \(y' = 2Ax\cdot \cos\left(Ax^2 + B\right)\)
- \(\displaystyle y' = \frac{Bx}{\sqrt{A + Bx^2}}\)
- \(y' = B\cdot\sin(Bx)\)
- \(y' = -2Ax\cdot\sin(Ax^2 + B)\)
- \(y' = x\left(B\cdot e^{Bx}\right) + e^{Bx} = (Bx+1)\cdot e^{Bx}\)
- \(y' = A\cdot e^{Ax} + A\cdot e^{-Ax}\)
- \(\displaystyle y' = \frac{A\cdot\sin(Bx) - Ax\cdot B\cdot\cos(Bx)}{\sin^2(Bx)}\)
- \(\displaystyle y' = \frac{(Cx+D)A - (Ax+B)C}{(Cx+D)^2} = \frac{AD - BC}{(Cx+D)^2}\)
-
- \(y' = AB - 2Ax\)
- \(x = \frac{AB}{2A} = \frac{B}{2}\)
- \(y'' = -2A\)
-
- \(y' = 2ABx - 3Ax^2 = Ax(2B - 3x)\)
- \(x = 0\), \(\frac{2B}{3}\)
- \(y'' = 2AB - 6Ax\)
-
- \(y' = 3Ax^2 + 2Bx = x(3Ax + 2B)\)
- \(x = 0\), \(-\frac{2B}{3A}\)
- \(y'' = 6Ax + 2B\)
- \(\displaystyle \frac{d}{dx}\left(\arctan(x^2)\right) = \frac{2x}{1 + x^4}\)
- \(\displaystyle \mbox{D}\left(\arctan(e^x)\right) = \frac{1}{1 + \left(e^x\right)^2}\cdot e^x = \frac{e^x}{1 + e^{2x}}\)
- \(\displaystyle \mbox{D}(\arcsin(x^3)) = \frac{3x^2}{\sqrt{1 - x^6}}\)
- \(\displaystyle \frac{d}{dt}\left(\arcsin(e^t)\right) = \frac{1}{\sqrt{1 - (e^t)^2}}\cdot e^t = \frac{e^t}{\sqrt{1 - e^{2t}}}\)
- \(\displaystyle \frac{d}{dx}\left(\ln(\sin(x) )\right) = \frac{1}{\sin(x)} \cdot \cos(x) = \cot(x)\)
- \(\frac{d}{ds}\left(\ln(e^s)\right) = \frac{1}{e^s} \cdot e^s = 1\) or \(\frac{d}{ds}\left(\ln(e^s)\right) = \frac{d}{ds}(s) = 1\)
Section 2.5
- \(\displaystyle \mbox{D}(\ln(5x)) = \frac{1}{5x}\cdot 5 = \frac{1}{x}\)
- \(\displaystyle \mbox{D}(\ln(x^k)) = \frac{1}{x^k} \cdot k x^{k-1} = \frac{k}{x}\)
- \(\displaystyle \mbox{D}(\ln(\cos(x))) = \frac{1}{\cos(x)} \cdot (-\sin(x)) = -\tan(x)\)
- \(\displaystyle \mbox{D}(\log_2(5x)) = \frac{1}{5x} \cdot \frac{1}{\ln(2)} \cdot (5) = \frac{1}{x\ln(2)}\)
- \(\displaystyle \mbox{D}(\ln(\sin(x))) = \frac{1}{\sin(x)} \cdot \cos(x) = \cot(x)\)
- \(\displaystyle \mbox{D}(\log_2(\sin(x))) = \frac{1}{\sin(x)} \cdot \frac{1}{\ln(2)} \cdot \cos(x) = \frac{\cot(x)}{\ln(2)}\)
- \(\displaystyle \mbox{D}(\log_5(5^x)) = \mbox{D}(x) = 1\)
- \(\displaystyle \mbox{D}(x\cdot\ln(3x)) = x\cdot \frac{1}{3x}\cdot 3 + \ln(3x) \cdot 1 = 1 + \ln(3x)\)
- \(\displaystyle \mbox{D}\left(\frac{\ln(x)}{x}\right) = \frac{x\cdot \frac{1}{x} - \ln(x)\cdot 1}{x^2} = \frac{1 - \ln(x)}{x^2}\)
- \(\displaystyle \mbox{D}\left(\ln\left((5x-3)^{\frac12}\right)\right) = \frac{1}{(5x-3)^{\frac12}} \cdot \mbox{D}\left((5x-3)^{\frac12}\right) = \frac{1}{(5x-3)^{\frac12}} \cdot \frac12 (5x-3)^{-\frac12} \cdot\mbox{D}(5x-3) = \frac52 \cdot \frac{1}{5x-3}\)
- \(\displaystyle \mbox{D}\left(\cos(\ln(w))\right) = -\sin(\ln(w))\cdot \frac{1}{w} = -\frac{\sin(\ln(w))}{w}\)
- \(\displaystyle \frac{d}{dt}\left(\sqrt{\ln(t +1)}\right) = \frac{1}{2(t+1)}\)
- \(\displaystyle \mbox{D}\left(5^{\sin(x)}\right) = 5^{\sin(x)} \cdot \ln(5) \cdot \cos(x)\)
- \(\frac{1}{\sec(x) + \tan(x)} \cdot (\sec(x)\tan(x) + \sec^2(x)) = \sec(x)\)
- \(f(x) = \ln(x), f'(x) = \frac{1}{x}\). Let \(P = (p, \ln(p))\). So we need \(y - \ln(p) = \frac{1}{p} (x - p)\) with \(x = 0\) and \(y = 0\): \(-ln(p) = - 1 \Rightarrow p = e\), hence \(P = (e, 1)\).
- \(\displaystyle 100(-1)(1 + Ae^{-t})^{-2}\cdot (Ae^{-t})(-1) = \frac{100 Ae^{-t}}{(1 + Ae^{-t})^2}\)
- \(f(x) = 8\ln(x) \, +\) any constant
- \(f(x) = \ln(3 \, + \sin(x)) +\) any constant
- \(g(x) = \frac35 e^{5x} \, +\) any constant
- \(f(x) = e^{x^2} \, +\) any constant
- \(h(x) = \ln(\sin(x)) \, +\) any constant
-
- When \(t = 0\), \(A\) is at \((0,1)\) and \(B\) is at \((0,1)\). When \(t = 1\), \(A\) is at \((1,3)\) and \(B\) is at \((1,3)\).
- Both robots traverse the same path (the line segment \(y = 2x+1\) for \(0\leq x \leq 1\)):

- \(\frac{dy}{dx} = 2\) for each, because \(y = 2x + 1\).
- \(A\): \(\frac{dx}{dt} = 1\), \(\frac{dy}{dt} = 2\), speed \(= \sqrt{1^2 + 2^2} = \sqrt{5}\)
\(B\): \(\frac{dx}{dt} = 2t\), \(\frac{dy}{dt} = 4t\), speed \(= \sqrt{(2t)^2 + (4t)^2}\) \(= 2\sqrt{5}t\). At \(t=1\), \(B\)'s speed is \(2\sqrt{5}\). - Moves along the same path \(y = 2x + 1\), but to the right and up for about \(1.57\) minutes, reverses direction and returns to its starting point, then continues left and down for \(1.57\) minutes, reverses, and continues to oscillate.
- When \(t=1\): \(\frac{dx}{dt} = +\), \(\frac{dy}{dt} = -\), \(\frac{dy}{dx} = -\). When \(t=3\), \(\frac{dx}{dt} = -\), \(\frac{dy}{dt} = -\), \(\frac{dy}{dx} = +\).
-
- \(x(t) = R(t - \sin(t))\), \(y(t) = R(1 - \cos(t))\):
![A red graph of the curve (R(t - \sin(t)),R(1 - \cos(t))) on a [0,4pi]X[0,2R] grid.](https://math.libretexts.org/@api/deki/files/140296/ans205_47.png?revision=1)
- \(\frac{dx}{dt} = R(1 -\cos(t))\), \(\frac{dy}{dt} = R\sin(t)\), so \(\frac{dy}{dx} = \frac{\sin(t)}{1-\cos(t)}\). When \(t = \frac{\pi}{2}\), then \(\frac{dx}{dt} = R\) and \(\frac{dy}{dt} = R\) so \(\frac{dy}{dx} = 1\) and speed \(\sqrt{R^2 + R^2} = R\sqrt{2}\). When \(t = \pi\), \(\frac{dx}{dt} = 2R\) and \(\frac{dy}{dt} = 0\) so \(\frac{dy}{dx} = 0\) and speed = \(\sqrt{(2R)^2 + 0^2} = 2R\).
- \(x(t) = R(t - \sin(t))\), \(y(t) = R(1 - \cos(t))\):
-
- The ellipse \(\left(\frac{x}{3}\right)^2 + \left(\frac{y}{5}\right)^2 = 1\).
- The ellipse \(\left(\frac{x}{A}\right)^2 + \left(\frac{y}{B}\right)^2 = 1\) if \(A \neq 0\) and \(B \neq 0\). If \(A = 0\), the motion is oscillatory along the \(x\)-axis; if \(B = 0\), the motion is oscillatory along the \(y\)-axis.
- \(\left(3\cdot\cos(t), -5\cdot\sin(t)\right)\) works.
Section 2.6
- \(V = \frac43 \pi r^3 \Rightarrow \frac{dV}{dt} = 4\pi r^2 \cdot \frac{dr}{dt}\). We know \(\left.\frac{dr}{dt}\right|_{r=3} = 2\) in/min, so \(\left.\frac{dV}{dt}\right|_{r=3} = 4\pi(3\mbox{ in})^2 (2\mbox{ in/min}) = 72\pi\) in\(^3\)/min \(\approx 226.19\) in\(^3\)/min.
-
- \(A = \frac12 bh \Rightarrow \frac{dA}{dt} = \frac12\left[b \frac{dh}{dt} + h\frac{db}{dt}\right]\) so with \(b = 15\) in, \(h = 13\) in, \(\frac{db}{dt} = 3\, \frac{\mbox{in}}{\mbox{hr}}\), \(\frac{dh}{dt} = -3 \, \frac{\mbox{in}}{\mbox{hr}}\):\[\frac{dA}{dt} = \frac12\left[(15\mbox{ in})\left(-3\, \frac{\mbox{in}}{\mbox{hr}}\right) + (13\mbox{ in})\left(3\, \frac{\mbox{in}}{\mbox{hr}}\right)\right]\nonumber\]which is \(<0\), so \(A\) is decreasing.
- Hypotenuse \(C = \sqrt{b^2 + h^2}\) so:\[\displaystyle \frac{dC}{dt} = \frac{b \frac{db}{dt} + h \frac{dh}{dt}}{\sqrt{b^2 + h^2}} = \frac{15(3) + 13(-3)}{\sqrt{15^2 + 13^2}}\nonumber\] which is \(>0\) so \(C\) is increasing.
- Perimeter \(P = b + h + C\) so:\[\frac{dP}{dt} = \frac{db}{dt} + \frac{dh}{dt} + \frac{dC}{dt} = 3 + (-3) + \frac{6}{\sqrt{394}}\nonumber\]which is \(> 0\) so \(P\) is increasing.
-
- Perimeter \(P = 2x + 2y \Rightarrow \frac{dP}{dt} = 2\frac{dx}{dt} + 2\frac{dy}{dt} = 2(3\mbox{ ft/sec}) + 2(-2\mbox{ ft/sec}) = 2\) ft/sec.
- Area \(A = xy \Rightarrow \frac{dA}{dt} = x \frac{dy}{dt} + y\frac{dx}{dt} \Rightarrow \frac{dA}{dt} = (12\mbox{ ft})\left(-2\, \frac{\mbox{ft}}{\mbox{sec}}\right) + (8\mbox{ ft})\left(3\, \frac{\mbox{ft}}{\mbox{sec}}\right) = 0\) ft\(^2\)/sec.
- Volume \(V = \pi r^2 h = \pi r^2\left(\frac13\right) \Rightarrow \frac{dV}{dt} = \frac{2\pi}{3} r \cdot \frac{dr}{dt}\). So when \(r = 50\) ft and \(\frac{dr}{dt} = 6\,\frac{\mbox{ft}}{\mbox{hr}}\), we have \(\frac{dV}{dt} = \frac{2\pi}{3} (50\mbox{ ft})\left(6\, \frac{\mbox{ft}}{\mbox{hr}}\right) = 200\pi \, \frac{\mbox{ft}^3}{\mbox{hr}} \approx 628.32\,\frac{\mbox{ft}^3}{\mbox{hr}}\).
- \(w(t) = h(t)\) for all \(t\) so \(\frac{dw}{dt} = \frac{dh}{dt}\). \(V = \frac13 \pi r^2 h\) and \(r = \frac{w}{2} = \frac{h}{2}\) so \(V = \frac13 \pi\left(\frac{h}{2}\right)^2 h = \frac{\pi}{12} h^3 \Rightarrow \frac{dV}{dt} = \frac{\pi}{4} h^2 \frac{dh}{dt}\). When \(h = 500\) ft and \(\frac{dh}{dt} = 2\,\frac{\mbox{ft}}{\mbox{hr}}\), then \(\frac{dV}{dt} = \frac{\pi}{4}(500)^2(2) = 125000\pi\,\frac{\mbox{ft}^3}{\mbox{hr}}\).
- Let \(x\) be the distance from the lamp post to the person and \(L\) be the length of the shadow (both in feet). By similar triangles, \(\frac{L}{6} = \frac{x}{8} \Rightarrow L = \frac34 x\). We also know that \(\frac{dx}{dt} = 3\,\frac{\mbox{ft}}{\mbox{sec}}\).
- \(\frac{dL}{dt} = \frac34 \frac{dx}{dt} = \frac34\left(3\,\frac{\mbox{ft}}{\mbox{sec}}\right) = 2.25\,\frac{\mbox{ft}}{\mbox{sec}}\)
- \(\frac{d}{dt}\left(x + L\right) = \frac{dx}{dt} + \frac{dL}{dt} = 5.25\,\frac{\mbox{ft}}{\mbox{sec}}\)
-
- \(\sin(35^{\circ}) = \frac{h}{500} \Rightarrow h = 500\sin(35^{\circ}) \approx 287\) ft
- \(L =\) length of the string so \(h = L\sin(35^{\circ})\) and \(\frac{dh}{dt} = \sin(35^{\circ}) \frac{dL}{dt} \approx (0.57)\left(10\,\frac{\mbox{ft}}{\mbox{sec}}\right) = 5.7\,\frac{\mbox{ft}}{\mbox{sec}}\)
- \(V = s^3 - \frac43 \pi r^3 \Rightarrow \frac{dV}{dt} = 3s^2 \frac{ds}{dt} - 4\pi r^2 \frac{dr}{dt}\) so when \(r = 4\) ft, \(\frac{dr}{dt} = 1\,\frac{\mbox{ft}}{\mbox{hr}}\), \(s = 12\) ft and \(\frac{ds}{dt} = 3\,\frac{\mbox{ft}}{\mbox{hr}}\): \(\frac{dV}{dt} = 3(12\,\mbox{ft})^2\left(3\,\frac{\mbox{ft}}{\mbox{hr}}\right) - 4\pi(4\,\mbox{ft})^2 \left(1\,\frac{\mbox{ft}}{\mbox{hr}}\right) \approx 1094.94\,\frac{\mbox{ft}^3}{\mbox{hr}}\). The volume is increasing at about 1,095 \(\frac{\mbox{ft}^3}{\mbox{hr}}\).
- Given: \(\frac{dV}{dt} = k\cdot 2\pi r^2\) with \(k\) constant. We also have \(V = \frac23 \pi r^3 \Rightarrow \frac{dV}{dt} = 2\pi r^2 \frac{dr}{dt}\) so \(k\cdot 2\pi r^2 = 2\pi r^2 \frac{dr}{dt} \Rightarrow \frac{dr}{dt} = k\). The radius \(r\) is changing at a constant rate.
-
- \(A = 5x\)
- \(\frac{dA}{dx} = 5\) for all \(x > 0\).
- \(A = 5t^2\)
- \(\frac{dA}{dt} = 10t\). When \(t = 1\), \(\frac{dA}{dt} = 10\); when \(t = 2\), \(\frac{dA}{dt} = 20\); when \(t = 3\), \(\frac{dA}{dt} = 30\).
- \(A = 10 + 5\cdot\sin(t) \Rightarrow \frac{dA}{dt} = 5\cdot\cos(t)\).
- In (b) and (c) we must use radians because our formulas for derivatives of trigonometric functions assume angles are measured in radians.
- \(\tan(10^{\circ}) = \frac{40}{x} \Rightarrow x = \frac{40}{\tan(10^{\circ})}\approx 226.9\) ft.
- \(x = \frac{40}{\tan(\theta)} = 40\cot(\theta) \Rightarrow \frac{dx}{dt} = -40\csc^2(\theta) \frac{d\theta}{dt}\) \(\Rightarrow \frac{d\theta}{dt} = -\frac{\sin^2(\theta)}{40}\frac{dx}{dt}\) so when \(\theta = 10^{\circ} \approx 0.1745\) radians and \(\frac{dx}{dt} = -25\,\frac{\mbox{ft}}{\mbox{min}}\):\[\frac{d\theta}{dt} = -\frac{\sin^2(0.1745)}{40}(-25) \approx \frac{(0.1736)^2(25)}{40}\nonumber\]\(\approx 0.0188\,\frac{\mbox{rad}}{\mbox{min}} \approx 1.079\,\frac{\circ}{\mbox{min}}\).
- \(\frac{dx}{dt} = -40\csc^2(\theta) \frac{d\theta}{dt} = \frac{-40}{\sin^2(\theta)}\frac{d\theta}{dt}\) so when \(\theta = 10^{\circ} \approx 0.1745\) rad and \(\frac{d\theta}{dt} = 2\,\frac{\circ}{\mbox{min}} \approx 0.0349\,\frac{\mbox{rad}}{\mbox{min}}\):\[\frac{d\theta}{dt} \approx \frac{-40}{(0.1736)^2}(0.0349) \approx -46.3\,\frac{\mbox{ft}}{\mbox{min}}\nonumber\](The “-” indicates the distance to the sign is decreasing: you are approaching the sign.) Your speed is \(46.3\,\frac{\mbox{ft}}{\mbox{min}}\).
Section 2.7
- The locations of \(x_1\) and \(x_2\) appear below:

- \(x_0 = 1\): a; \(x_0 = 5\): b
- \(x_0 = 1\): \(1\), \(2\), \(1\), \(2\), \(1\), …
\(x_0 = 5\): \(x_1\) is undefined because \(f'(5) = 0\) - If \(f\) is differentiable, then \(f'(x_0) = 0\) and \(x_1 = x_0 - \frac{f(x_0)}{f'(x_0)}\) is undefined.
- \(f(x) = x^4 - x^3 - 5 \Rightarrow f'(x) = 4x^3 - 3x^2\) so \(x_0 = 2 \Rightarrow x_1 = 2 - \frac{3}{20} = \frac{37}{20} = 1.85 \Rightarrow x_2 = 1.85 - \frac{1.85^4 - 1.85^3 - 5}{4(1.85)^3 - 3(1.85)^2} \approx 1.824641\)
- \(f(x) = x - \cos(x) \Rightarrow f'(x) = 1 + \sin(x)\) so \(x_0 = 0.7 \Rightarrow x_1 = 0.7394364978 \Rightarrow x2 = 0.7390851605\), so root \(\approx 0.74\).
- To solve \(\frac{x}{x + 3} = x^2 - 2\) we search for roots of \(f(x) = x^2 - 2 - \frac{x}{x + 3}\). If \(x_0 = -4\), then the iterates \(x_n \rightarrow -3.3615\); if \(x_0= -2\), then \(x_n \rightarrow -1.1674\); if \(x_0 = 2\), then the iterates \(x_n \rightarrow 1.5289\).
- For \(x^5 - 3 = 0\) and \(x_0 = 1\), \(x_n \rightarrow 1.2457\).
- \(f(x) = x^3 - A \Rightarrow f'(x) = 3x^2\) so:\[x_{n+1} = x_n - \frac{x_n^3 - A}{3x_n^2} = \frac13\left[2x_n + \frac{A}{x_n^2}\right]\nonumber\]
-
- \(2(0) - \lfloor2(0)\rfloor = 0 - 0 = 0\)
- \(2(\frac12) - \lfloor2(\frac12)\rfloor = 1 - 1 = 0\)
\(2(\frac14) - \lfloor2(\frac14)\rfloor = \frac12 - 0 = \frac12 \rightarrow 0\)
\(2(\frac18) - \lfloor2(\frac18)\rfloor = \frac14 - 0 = \frac14 \rightarrow \frac12 \rightarrow 0\)
\(2(\frac{1}{2^n}) - \lfloor2(\frac{1}{2^n})\rfloor = \frac{1}{2^{n-1}} - 0 = \frac{1}{2^{n-1}}\)
\(\rightarrow \frac{1}{2^{n-2}} \rightarrow \cdots \rightarrow \frac14 \rightarrow \frac12 \rightarrow 0\)
-
- If \(0 \leq x \leq \frac12\), then \(f\) stretches \(x\) to twice its value, \(2x\). If \(\frac12 < x \leq 1\), then \(f\) stretches \(x\) to twice its value (\(2x\)) and “folds” the part above the value \(1\) (\(2x - 1\)) to below \(1\): \(1 - (2x - 1) = 2 - 2x\).
- \(f(\frac23) = \frac23\)
\(f(\frac25) = \frac45\), \(f(\frac45) = \frac25\), and the values continue to cycle.
\(f(\frac27) = \frac47\), \(f(\frac47) = \frac67\), \(f(\frac67) = \frac27\), and the values continue to cycle.
\(f(\frac29) = \frac49\), \(f(\frac49) = \frac89\), \(f(\frac89) = \frac29\), and the values continue to cycle. - \(0.1\), \(0.2\), \(\mathbf{0.4}\), \(0.8\), \(\mathbf{0.4}\), \(0.8\), and the pair of values \(0.4\) and \(0.8\) continue to cycle.
\(0.105\), \(0.210\), \(0.42\), \(0.84\), \(\mathbf{0.32}\), \(0.64\), \(0.72\), \(0.56\), \(0.88\), \(0.24\), \(0.48\), \(0.96\), \(0.08\), \(0.16\), \(\mathbf{0.32}\), … \(0.11\), \(0.22\), \(0.44\), \(\mathbf{0.88}\), \(0.24\), \(0.48\), \(0.96\), \(0.08\), \(0.16\), \(0.32\), \(0.64\), \(0.72\), \(0.56\), \(\mathbf{0.88}\), … - Probably so.
Section 2.8
-
- The desired points appear below:
![A segment of a red concave-down curve labeled 'g' graphed on the grid [0,3]X[0,3] together with a blue line segment that is tangent to the red curve at the point where x = 2. A black dot on the curve is denoted by an arrow labelling the point (2 + Delta x, g(2 + Delta x)). Another black dot is above the first dot on the bllue line segment, denoted by an arrow and labeled (2 + Delta x, g(2) + g'(2)*Delta x). The horizontal distance between the points on the horizontal axis where x = 2 and x = 2 + Delta x is denoted as Delta x. The vertical distance between the two black dots is denoted by a double arrow labeled 'error.'](https://math.libretexts.org/@api/deki/files/140304/ans208_1.png?revision=1&size=bestfit&width=479&height=248)
- The “error” appears in the figure above.
- The desired points appear below:
-
- \(f(81) = 9\) and \(f'(81) = \frac{1}{18}\) so tangent line is \(y - 9 = \frac{1}{18} (x - 81)\) or \(y = \frac{1}{18} (x - 81) + 9\) and \(\sqrt{80} = f(80) \approx \frac{1}{18} (80 - 81) + 9 = \frac{161}{18} \approx 8.944\)
- \(f(0) = 0\) and \(f'(0) = 1\) so tangent line is \(y = x\) and \(\sin(0.3) = f(0.3) \approx 0.3\)
-
- \(f(1) = 0\) and \(f'(1) = 1\) so tangent line is \(y - 0 = 1(x - 1)\) or \(y = x-1\) and \(\ln(1.3) = f(1.3) \approx 1.3 - 1 = 0.3\)
- \(f(0) = 1\) and \(f'(0) = 1\) so tangent line is \(y - 1 = 1(x - 0)\) or \(y = 1 + x\) and \(e^{0.1} = f(0.1) \approx 1.1\)
- \(f(1) = 1\) and \(f'(1) = 5\) so tangent line is \(y - 1 = 5(x - 1)\) or \(y = 5x-4\) and \((1.03)^5 \approx 5(0.03)-4 = 1.15\)
- \(f(x) = (1 + x)^n \Rightarrow f'(x) = n(1 + x)^{n-1}\) so \(f(0) = 1\) and \(f'(0) = n\), hence tangent line is \(y - 1 = n(x - 0)\) or \(y = 1 + nx\) and \((1 + x)^n \approx 1 + nx\) (when \(x\) is close to \(0\))
-
- \(f(x) = (1 - x)^n \Rightarrow f'(x) = -n(1 - x)^{n-1}\) so \(f(0)=1\) and \(f'(0) = -n\), hence tangent line is \(y - 1 = -n(x - 0)\) or \(y = 1 - nx\) and \((1 - x)^n \approx 1 - nx\) (when \(x\) is close to \(0\))
- \(f(x) = \sin(x) \Rightarrow f'(x) = \cos(x)\) so \(f(0) = 0\) and \(f'(0) = 1\), hence tangent line is \(y - 0 = 1(x - 0)\) or \(y = x\) and \(\sin(x) \approx x\) (for \(x\) close to \(0\))
- \(f(x) = e^x \Rightarrow f'(x) = e^x\) so \(f(0) = 1\) and \(f'(0) = 1\), hence tangent line is \(y - 1 = 1(x - 0)\) or \(y = x + 1\) and \(e^x \approx x + 1\) (for \(x\) near \(0\))
-
- \(f(x) = \ln(1 + x) \rightarrow f'(x) = \frac{1}{1+x}\) so \(f(0)=0\) and \(f'(0) = 1\), hence tangent line is \(y = x\) and \(\ln(1 + x) \approx x\)
- \(f(x) = \cos(x) \Rightarrow f'(x) = -\sin(x)\) so \(f(0) = 1\) and \(f'(0) = 0\), hence tangent line is \(y = 1\) and \(\cos(x) \approx 1\)
- \(f(x) = \tan(x) \Rightarrow f'(x) = \sec^2(x)\), so \(f(0) = 0\) and \(f'(0) = 1\), hence tangent line is \(y = x\) and \(\tan(x) \approx x\)
- \(f(x) = \sin\left(\frac{\pi}{2} + x\right) \Rightarrow f'(x) = \cos\left(\frac{\pi}{2} + x\right)\) so \(f(0) = 1\) and \(f'(0) = 0\), hence tangent line is \(y =1\) and \(\sin\left(\frac{\pi}{2} + x\right) \approx 1\).
-
- Area \(A(x) =(\mbox{base})(\mbox{height}) = x(x^2 +1) = x^3 + x \Rightarrow A'(x) = 3x^2 +1 \Rightarrow A'(2) = 13\) so \(\Delta A \approx A'(2)\cdot\Delta x = (13)(2.3 - 2) = 3.9\)
- \((\mbox{base})(\mbox{height}) = (2.3)((2.3)^2 + 1 ) = 14.467\) so actual \(\Delta A = 14.467 - (2)(2^2+1) = 4.467\)
- \(V = \pi r^2 h = 2\pi r^2\) and \(\Delta V = 2\pi\cdot 2r \Delta r = 4\pi r \Delta r\). Because \(V = 2\pi r^2 = 47.3\), we have \(r = \sqrt{\frac{47.3}{2\pi}} \approx 2.7437\) cm. We know \(\left|\Delta V\right| \leq 0.1\) so, using \(\Delta V = 4\pi r \Delta r\), we have \(0.1 \geq 4\pi (2.7437)\left|\Delta r\right|\) and \(\left|\Delta r\right| \leq \frac{0.1}{4\pi (2.7437)} \approx 0.0029\) cm. The required tolerance is \(\pm 0.0029\) cm. (Reality check: A coin 2 cm high is quite unusual; 47.3 cm\(^3\) of gold weighs around 2 pounds!)
- \(V = x^3 \Rightarrow \Delta V \approx 3x^2 \Delta x\), \(V = 87 \Rightarrow x = \sqrt[3]{87} \approx 4.431\) cm so \(\Delta x \approx \frac{\Delta V}{3x^2} \approx \frac{2}{3(4.431)^2} \approx 0.034\) cm
- With \(P = 2\pi\sqrt{\frac{L}{g}}\) and \(g = 32\,\frac{\mbox{ft}}{\mbox{sec}^2}\,\):
- \(P = 2\pi\sqrt{\frac{2}{32}} = \frac{\pi}{2} \approx 1.57\) sec
- \(1 = 2\pi\sqrt{\frac{L}{32}} \Rightarrow L = \frac{8}{\pi^2} \approx 0.81\) ft
- \(dP = \frac{2\pi}{\sqrt{32}}\cdot \frac{1}{2\sqrt{2}}\, dL = \frac{2\pi}{16}(0.1) \approx 0.039\) sec
- \(2\,\frac{\mbox{in}}{\mbox{hr}} = \frac16\,\frac{\mbox{ft}}{\mbox{hr}} = \frac{1}{21600}\,\frac{\mbox{ft}}{\mbox{sec}}\) so \(\frac{dP}{dt} = \frac{2\pi}{4\sqrt{2}}\cdot\frac{1}{2\sqrt{24}}\cdot\frac{1}{21600} \approx 5.25 \times 10^{-6} >0\) (increasing)
-
- \(df = f'(2)\, dx \approx (0)(1) = 0\)
- \(df = f'(4)\, dx \approx (0.3)(-1) = -0.3\)
- \(df = f'(3)\, dx \approx (0.5)(2) = 1\)
-
- \(f'(x) = 2x - 3 \Rightarrow df = (2x - 3)\, dx\)
- \(f'(x) = e^x \Rightarrow df = e^x\, dx\)
- \(f'(x) = 5\cos(5x) \Rightarrow df = 5\cos(5x)\, dx\)
- \(f'(x) = 3x^2 + 2 \Rightarrow df = (3x^2 + 2)\, dx\) so when \(x = 1\) and \(dx = 0.2\), \(df = (3\cdot1^2 + 2)(0.2) = 1\)
- \(f'(x) = \frac{1}{x} \Rightarrow df = \frac{1}{x}\, dx\) so when \(x = e\) and \(dx = -0.1\), \(df = \frac{1}{e}(-0.1) = -\frac{1}{10e}\)
- \(f'(x) = \frac{1}{\sqrt{2x + 5}} \Rightarrow df = \frac{1}{\sqrt{2x + 5}}\, dx\) so when \(x = 22\) and \(dx = 3\), \(df = \frac{1}{\sqrt{49}} (3) = \frac37\)
Section 2.9
-
- \(\displaystyle x^2 + y^2 = 100 \Rightarrow 2x + 2y\cdot y' = 0 \Rightarrow y' = -\frac{x}{y}\) so at \((6,8)\), \(\displaystyle y' = -\frac68 = -\frac34\)
- \(\displaystyle y = \sqrt{100 - x^2} \Rightarrow y' = \frac{-x}{\sqrt{100 - x^2}}\) so at \((6,8)\), \(\displaystyle y' = -\frac{6}{\sqrt{100 - 36}} = -\frac68 = -\frac34\)
-
- \(\displaystyle x^2 - 3xy + 7y = 5 \Rightarrow 2x - 3(y + xy') + 7y' = 0 \Rightarrow y' = \frac{3y - 2x}{7 - 3x} \Rightarrow \left. y'\right|_{(2,1)} = \frac{3-4}{7-6} = -1\)
- \(\displaystyle y = \frac{5 - x^2}{7 - 3x} \Rightarrow y' = \frac{(7 - 3x)(-2x) - (5 - x^2)(-3)}{(7 - 3x)^2}\) so at \((2,1)\), \(\displaystyle y' = \frac{(1)(-4) - (1)(-3)}{(1)^2} = -1\)
-
- \(\displaystyle \frac{x^2}{9} + \frac{y^2}{16} = 1 \Rightarrow \frac{2x}{9} + \frac{2y}{16} y' = 0 \Rightarrow y' = -\frac{16}{9}\cdot \frac{x}{y} \Rightarrow \left. y'\right|_{(0,4)} = 0\)
- \(\displaystyle y = 4\sqrt{1 - \frac{x^2}{9}} = \frac43\sqrt{9 - x^2} \Rightarrow y' = \frac43 \cdot \frac{-x}{\sqrt{9 - x^2}} \Rightarrow \left. y'\right|_{(0,4)} = 0\)
-
- \( \displaystyle \ln(y) + 3x - 7 = 0 \Rightarrow \frac{1}{y} y' + 3 = 0 \Rightarrow y' = -3y \Rightarrow \left. y'\right|_{(2,e)} = -3e\)
- \(\displaystyle y = e^{7-3x} \Rightarrow y' = -3 e^{7-3x} \Rightarrow \left. y'\right|_{(2,e)} = -3 e^{7-6} = -3e\)
-
- \(\displaystyle x^2 - y^2 = 16 \Rightarrow 2x - 2yy' = 0 \Rightarrow y' = \frac{x}{y} \Rightarrow \left. y'\right|_{(5,-3)} = -\frac53\)
- The point \((5, -3)\) is on the bottom half of the hyperbola so \(\displaystyle y = -\sqrt{x^2 - 16} \Rightarrow y' = -\frac{x}{\sqrt{x^2 - 16}} \Rightarrow \left. y'\right|_{(5,-3)} = -\frac{5}{\sqrt{25-16}} = -\frac53\)
- \(\displaystyle x = 4y - y^2 \Rightarrow 1 = 4y' - 2y\cdot y ' \Rightarrow y' = \frac{1}{4 - 2y}\). At \((3,1)\), \(y' = \frac{1}{4 - 2(1)} = \frac12\); at \((3,3)\), \(y' = \frac{1}{4 - 2(3)} = -\frac12\); at \((4,2)\), \(y' = \frac{1}{4 - 2(2)}\) is undefined (the tangent line is vertical).
- \(x = y^2 - 6y + 5 \Rightarrow 1 = 2y\cdot y' - 6y' \Rightarrow y' = \frac{1}{2y - 6}\). At \((5,0)\), \(y' = \frac{1}{2(0) - 6} = -\frac16\); at \((5,6)\), \(y' = \frac{1}{2(6) - 6} = \frac16\); at \((-4,3)\), \(y' = \frac{1}{2(3) - 6}\) is undefined (vertical tangent line).
- \(\displaystyle 3y^2 \cdot y' - 5y' = 10x \Rightarrow y' = \frac{10x}{3y^2 - 5} \Rightarrow m = \left. y'\right|_{(1,3)} = \frac{10}{22} = \frac{5}{11}\)
- \(\displaystyle y^2 + \sin(y) = 2x - 6 \Rightarrow 2y\cdot y' + \cos(y)\cdot y' = 2 \Rightarrow y' = \frac{2}{2y + \cos(y)} \Rightarrow m = \left. y'\right|_{(3,0)} = \frac{2}{0+1} = 2\)
- \(\displaystyle e^y + \sin(y) = x^2 - 3 \Rightarrow e^y \cdot y' + \cos(y) \cdot y' = 2x \Rightarrow y' = \frac{2x}{e^y + \cos(y)} \Rightarrow m = \left. y'\right|_{(2,0)} = %\frac{4}{1+1} = 2\)
- \(\displaystyle x^{\frac23} + y^{\frac23} = 5 \Rightarrow \frac23 x^{-\frac13} + \frac23 y^{-\frac13}y' = 0 \Rightarrow y' = %-\left(\frac{x}{y}\right)^{-\frac13} = -\left(\frac{y}{x}\right)^{\frac13} \Rightarrow m = \left. y'\right|_{(8,1)} = -\left(\frac18\right)^{\frac13} = -\frac12\)
- \(\displaystyle 2x + x\cdot y' + y + 2y\cdot y' + 3 - 7y ' = 0 \Rightarrow y' = \frac{-2x - y - 3}{x + 2y - 7} \Rightarrow \left. y'\right|_{(1,2)} = \frac{-2(1) - (2) - 3}{(1) + 2(2) - 7} = \frac72\)
- Explicitly: \(y = Ax^2 + Bx + C \Rightarrow y' = 2Ax + B\)
Implicitly: \(x = Ay^2 + By + C \Rightarrow 1 = 2Ayy ' + By' \Rightarrow y' = \frac{1}{2Ay + B}\) - \(Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 \Rightarrow 2Ax + Bx\cdot y' + By + 2Cy\cdot y' + D + Ey' = 0 \Rightarrow y' = \frac{-2Ax - By - D}{Bx + 2Cy + E}\)
- \(\displaystyle x^2 + y^2 = r^2\Rightarrow 2x + 2y\cdot y' = 0 \Rightarrow y' = -\frac{x}{y}\) so the slope of the tangent line is \(-\frac{x}{y}\). The slope of the line through the points \((0,0)\) and \((x,y)\) is \(\frac{y}{x}\), so the slopes of the lines are negative reciprocals of each other and the lines are perpendicular.
- From the solution to problem 23, we know that \(y' = \frac{-2x - y - 3}{x + 2y - 7}\) so \(y' = 0\) when \(-2x - y - 3 = 0 \Rightarrow y = -2x - 3\). Substituting \(y = -2x - 3\) into the original equation, we have: \begin{align*}x^2 + x(-2x - 3) &+ (-2x - 3)^2\\ &+ 3x - 7(-2x - 3) + 4 = 0\end{align*} \(\Rightarrow 3x^2 + 26x + 34 = 0 \Rightarrow x = \frac{-26 \pm \sqrt{26^2 - 4(3)(34)}}{2(3)}\) \(= \frac{-13 \pm \sqrt{67}}{3} \approx -1.605\) or \(-7.062\).
If \(x \approx -1.605\) (point \(A\)), then \(y = -2x - 3 \approx -2(-1.605) - 3 = 0.21\) so coordinates of \(A\) are \((-1.605, 0.21)\); if \(x \approx -7.062\) (point \(C\)), then \(y = -2x - 3 \approx -2(-7.062) - 3 = 11.124\) so \(C\) is \((-7.062, 11.124)\). - From the solution to 29, point \(C\) is \((-7.062, 11.124)\). At \(D\), \(y' = \frac{-2x - y - 3}{x + 2y - 7}\) is undefined so \(x + 2y - 7 = 0 \Rightarrow x = 7 - 2y\). Substituting \(x = 7 - 2y\) into the original equation:\[(7-2y)^2 + (7-2y)y + y^2 + 3(7-2y) - 7y + 4 = 0\nonumber\]so \(3y^2 - 34y + 74 = 0 \Rightarrow y = \frac{34 \pm \sqrt{34^2 - 4(3)(74)}}{2(3)} = \frac{17 \pm \sqrt{67}}{3} \approx 8.395\) or \(2.938\).
If \(y \approx 2.938\) (point \(D\)), then \(x = 7 - 2y \approx 7 - 2(2.938) = 1.124\) so point \(D\) is \((1.124, 2.938)\). Similarly, point \(B\) is \((-9.79, 8.395)\). -
- Using the Product Rule: \(y = (x^2 + 5)^7(x^3 - 1)^4\) so: \begin{align*}y' &= (x^2 + 5)^7 \cdot 4(x^3 - 1)^3 \cdot 3x^2\\ &\qquad + 7(x^2 + 5)^6 \cdot 2x \cdot (x^3 - 1)^4\\ &= (x^2 + 5)^6(x^3 - 1)^3(2x)\left[6x^3 + 30x + 7x^3 - 7\right]\\ &= (x^2 + 5)^6(x^3 - 1)^3(2x)\left[13x^3 + 30x - 7\right]\end{align*}
- \(\displaystyle \ln(y) = 7\ln(x^2 + 5) + 4\ln(x^3 - 1)\) so:\[\frac{y'}{y} = \frac{14x}{x^2 + 5} + \frac{12x^2}{x^3 - 1}\nonumber\]and solving for \(y'\) yields: \begin{align*} y' &= y \left[\frac{14x}{x^2 + 5} + \frac{12x^2}{x^3 - 1}\right]\\\ &= (x^2 + 5)^7(x^3 - 1)^4\left[\frac{14x}{x^2 + 5} + \frac{12x^2}{x^3 - 1}\right]\end{align*} which is the same as part (a). (Really! It is!)
-
- \(y = x^5 (3x + 2)^4\) so: \begin{align*} y' &= x^5\mbox{D}\left((3x + 2)^4\right) + (3x + 2)^4 \mbox{D}\left(x^5\right)\\ &= x^5\cdot 4(3x + 2)^3(3) + (3x + 2)^4\cdot 5x^4\end{align*}
- \(\ln(y) = 5\ln(x) + 4\ln(3x + 2)\) so: \[\frac{y'}{y} = \frac{5}{x} + \frac{12}{3x + 2}\nonumber\]and solving for \(y'\) yields: \begin{align*} y' &= y\left[\frac{5}{x} + \frac{12}{3x + 2}\right]\\ &= \left[x^5 (3x + 2)^4\right] \cdot \left[\frac{5}{x} + \frac{12}{3x + 2}\right]\end{align*} which is the same as in part (a).
-
- \(\displaystyle y = e^{\sin(x)} \Rightarrow y' = e^{\sin(x)}\cdot\cos(x)\)
- \(\displaystyle \ln(y) = \sin(x) \Rightarrow \frac{y'}{y} = \cos(x) \Rightarrow y' = y\cdot\cos(x) = e^{\sin(x)}\cdot\cos(x)\)
-
- \(\displaystyle y = \sqrt{25 - x^2} \Rightarrow y' = \frac{-x}{\sqrt{25 - x^2}}\)
- \(\ln(y) = \frac12 \ln(25 - x^2)\) so:\[\frac{y'}{y} = \frac12\cdot\frac{-2x}{25 - x^2} = \frac{-x}{25 - x^2}\nonumber\]and solving for \(y'\) yields:\[y' = \sqrt{25 - x^2}\cdot\frac{-x}{25 - x^2} = \frac{-x}{\sqrt{25 - x^2}}\nonumber\]
- \(\displaystyle y = x^{\cos(x)} \Rightarrow \ln(y) = \cos(x)\cdot \ln(x) \Rightarrow \frac{y'}{y} = \cos(x)\cdot\frac{1}{x} - \ln(x)\cdot\sin(x)\) so:\[y' = y \left[ \frac{\cos(x)}{x} - \ln(x)\cdot\sin(x)\right] = x^{\cos(x)}\left[ \frac{\cos(x)}{x} - \ln(x)\cdot\sin(x)\right]\nonumber\]
- \(\displaystyle \ln(y) = 4\ln(x) + 7\ln(x - 2) + \ln(\sin(3x)) \Rightarrow \frac{y'}{y} = \frac{4}{x} + \frac{7}{x - 2} + \frac{3\cos(3x)}{\sin(3x)}\) so: \[y' = y \left[\frac{4}{x} + \frac{7}{x - 2} + 3\cot(3x)\right] = x^4 (x - 2)^7 \sin(3x)\left[\frac{4}{x} + \frac{7}{x - 2} + 3\cot(3x)\right]\nonumber\]
- \(\displaystyle \ln(y) = x\cdot\ln(3 + \sin(x)) \Rightarrow \frac{y'}{y} = x\cdot\frac{\cos(x)}{3 + \sin(x)} + \ln(3 + \sin(x))\) so:\[y' = (3 + \sin(x))^x \left[\frac{x \cos(x)}{3 + \sin(x)} + \ln(3 + \sin(x))\right]\nonumber\]
- \(f'(1) = 1(1.2) = 1.2\); \(f'(2) = 9(1.8) = 16.2\)
\(f'(3) = 64(2.1) = 134.4\) - \(f'(1) = 5(-1) = -5\); \(f'(2) = 2(0) = 0\)
\(f'(3) = 7(2) = 14\) - \(\displaystyle \ln(f\cdot g) = \ln(f) + \ln(g) \Rightarrow \frac{\mbox{D}(f\cdot g)}{f\cdot g} = \frac{f'}{f} + \frac{g'}{g}\) so \(\mbox{D}(f\cdot g) = (f\cdot g) \left[\frac{f'}{f} + \frac{g'}{g}\right] = f'\cdot g + g'\cdot f\)
- \(\displaystyle \ln\left(\frac{f}{g}\right) = \ln(f) - \ln(g) \Rightarrow \frac{\mbox{D}\left(\frac{f}{g}\right)}{\left(\frac{f}{g}\right)} = \frac{f'}{f} - \frac{g'}{g}\) so: \begin{align*}\mbox{D}\left(\frac{f}{g}\right) &= \left(\frac{f}{g}\right)\left[\frac{f'}{f} - \frac{g'}{g}\right] = \frac{f'}{g} - \frac{f\cdot g'}{g^2}\\ &= \frac{f\cdot g' - g\cdot f'}{g^2}\end{align*}
- \(\displaystyle \ln(f\cdot g \cdot h) = \ln(f) + \ln(g) + \ln(h) \Rightarrow \frac{\mbox{D}(f\cdot g \cdot h)}{f\cdot g \cdot h} = \frac{f'}{f} + \frac{g'}{g} + \frac{h'}{h}\) so: \begin{align*}\mbox{D}(f\cdot g \cdot h) &= (f\cdot g \cdot h)\left[\frac{f'}{f} + \frac{g'}{g} + \frac{h'}{h}\right]\\ &= f'\cdot g\cdot h + f\cdot g'\cdot h + f\cdot g\cdot h'\end{align*}
- \(\ln(a^x) = x\ln(a) \Rightarrow \frac{\mbox{D}(a^x)}{a^x} = \ln(a) \Rightarrow \mbox{D}(a^x) = a^x\ln(a)\)


