3.A: Answers

Section 3.1

1. Local maximums at \(x = 3\), \(x = 5\), \(x = 9\) and \(x = 13\); global maximum at \(x = 13\). Local minimums at \(x = 1\), \(x = 4.5\), \(x = 7\) and \(x = 10.5\); global minimum at \(x = 7\).
3. \(f(x) = x^2 + 8x + 7 \Rightarrow f'(x) = 2x + 8\), which is defined for all values of \(x\); \(f '(x) = 0\) when \(x = -4\), so \(x = -4\) is a critical number. There are no endpoints. The only critical number is \(x = -4\), so the only critical point is \((-4, f(-4)) = (-4, -9)\), which is the global (and local) minimum.
5. \(f(x) = \sin(x) \Rightarrow f'(x) = \cos(x)\), which is defined for all values of \(x\); \(f'(x) = 0\) when \(x = \frac{\pi}{2} + k\pi\) so those values are critical numbers. There are no endpoints. \(f(x) = \sin(x)\) has local and global maximums at \(x = \frac{\pi}{2} + 2k\pi\) and global and local minimums at \(x = \frac{3\pi}{2} + 2k\pi\).
7. \(f(x) = \sqrt[3]{x} = x^{\frac13} \Rightarrow f'(x) = \frac13 x^{-\frac23} = \frac{1}{3\sqrt[3]{x^2}}\), which is defined for all values of \(x\) except \(x=0\), and \(f'(x) \neq 0\) for all \(x\), so \(x=0\) is the only critical number. There are no endpoints. the function \(f(x) = \sqrt[3]{x}\) has no global or local extrema.
9. \(f(x) = x e^{5x} \Rightarrow f'(x) = e^{5x}\left[5x+1\right]\), which is defined for all values of \(x\); \(f'(x) = 0\) when \(5x+1 = 0 \Rightarrow x = -\frac15\) so this is the only critical number. There are no endpoints. The function \(f(x) = x e^{5x}\) has a local and global minimum at \(x = -\frac15\) and no other extrema.
11. \(\displaystyle f(x) = (x - 1)^2 (x - 3) \Rightarrow f'(x) = (x - 1)^2 + 2(x - 1)(x - 3) = (x - 1)(3x - 7)\), which is defined for all values of \(x\); \(f'(x) = 0\) when \(x = 1\) and \(x = \frac73\) so those values are critical numbers. There are no endpoints. The only critical points are \((1, 0)\), which is a local maximum, and \(\left(\frac73, -\frac{32}{27}\right)\), which is a local minimum. When the interval is the entire real number line, this function does not have any global extrema.
13. \(f(x) = 2x^3 - 96x + 42 \Rightarrow f'(x) = 6x^2 - 96\), which is defined for all values of \(x\); \(f'(x) = 6(x + 4)(x - 4) = 0\) when \(x = -4\) and \(x = 4\) so those values are critical numbers. There are no endpoints. The only critical points are \((-4, 298)\), which is a local maximum, and \((4,-214)\), which is a local minimum. When the interval is the entire real number line, this function does not have a global maximum or global minimum.
15. \(\displaystyle f(x) = e^{-(x-2)^2} \Rightarrow f'(x) = -2(x - 2)e^{-(x-2)^2}\), which is defined for all \(x\); \(f'(x) = 0\) only when \(x = 2\), so that is a critical number. There are no endpoints. The only critical point is \((2, 1)\), which is a local and global maximum. When the interval is the entire real number line, this function does not have a local or global minimum.
17. \(\displaystyle f(x) = \frac{x}{1+x^2}\Rightarrow f'(x) = \frac{1-x^2}{(1+x^2)^2}\), which is defined for all \(x\); \(f'(x) = 0\) only when \(x = \pm 1\), so these are the only critical numbers. There are no endpoints. The critical point \(\left(-1, -\frac12\right)\) is a local and global minimum; the critical point \(\left(1, \frac12\right)\) is a local and global maximum.
19. \(f(x) = (x-2)^{\frac23} \Rightarrow f'(x) = \frac23 (x-2)^{-\frac13} = \frac{2}{3\sqrt[3]{x-2}}\), which is defined for all values of \(x\) except \(x=2\), and \(f'(x) \neq 0\) for all \(x\) so \(x=2\) is the only critical number. There are no endpoints. The function \(f(x) = (x-2)^{\frac23}\) has a global and local minimum at \(x=2\) and no other extrema.
21. \(f(x) = (x^2-4)^{\frac13} \Rightarrow f'(x) = \frac23 (x^2-4)^{-\frac23}\cdot 2x = \frac{2x}{3\sqrt[3]{(x^2-4)^2}}\), which is defined for all values of \(x\) except \(x=\pm 2\), and \(f'(x) = 0\) only when \(x = 0\), so \(x=-2\), \(x=0\) and \(x=2\) are the only critical numbers. There are no endpoints. The function \(f(x) = \sqrt[3]{x^2-4}\) has a global and local minimum at \(x=0\) and no other global or local extrema.
23. 
25. \(f(x) = x^2 - 6x + 5 \Rightarrow f'(x) = 2x - 6\), which is defined for all values of \(x\); \(f'(x) = 0\) only when \(x = 3\), so that is a critical number. The endpoints are \(x = -2\) and \(x = 5\). The critical points are \((3, -4)\), which is the local and global minimum, \((-2, 21)\), which is a local and global maximum, and \((5, 0)\), which is a local maximum.
27. \(f(x) = 2 - x^3 \Rightarrow f'(x) = -3x^2\), which is defined for all values of \(x\); \(f'(x) = 0\) only when \(x = 0\), so that is a critical number. The endpoints are \(x = -2\) and \(x = 1\), which are also critical numbers. The critical points are \((-2, 10)\), which is a local and global maximum, \((0,2)\), which is not a local or global maximum or minimum, and \((1,1)\), which is a local and global minimum.
29. \(f'(x) = 3x^2 - 3 = 3(x - 1)(x + 1)\), which is defined for all \(x\); \(f'(x) = 0\) only when \(x = -1\) and \(x = 1\), so these are critical numbers. The endpoints \(x = -2\) and \(x = 1\) are also critical numbers. The critical points are \((-2, 3)\), which is a local and global minimum on \([-2, 1]\), the point \((-1, 7)\), which is a local and global maximum on \([ -2, 1]\), and the point \((1, 3)\), which is a local and global minimum on \([ -2, 1]\).
31. \(f'(x) = 5x^4 - 20x^3 + 15x^2 = 5x^2(x^2 - 4x + 3) = 5x^2(x - 3)(x - 1)\), which is defined for all \(x\); \(f'(x) = 0\) only when \(x = 0\) or \(x = 1\) in the interval \([0, 2]\), so each of these values is a critical number. The endpoints \(x = 0\) and \(x = 2\) are also critical numbers. The critical points are \((0, 7)\), which is a local minimum, \((1, 8)\) which is a local and global maximum, and \((2, -1)\), which is a local and global minimum. (It is also true that \(f '(3) = 0\), but \(x = 3\) is not in the interval \([0, 2]\).)
33. \(f(x) = \frac{1}{x^2 + 1} \Rightarrow f'(x) = \frac{-2x}{(x^2 + 1)^2}\), which is defined for all values of \(x\); \(f'(x) = 0\) only when \(x = 0\), which is not in the interval \([1, 3]\) so \(x = 0\) is a not a critical number. The endpoints \(x = 1\) and \(x = 3\) are critical numbers. The critical points are \(\left(1, \frac12\right)\), which is a local and global maximum, and \(\left(3, \frac{1}{10}\right)\), which is a local and global minimum.
35. \(f'(x) = \frac32 \left(x^2+4\right)^{-\frac12}\cdot 2x -1 = \frac{3x}{\sqrt{x^2+4}} -1\), which exists for all \(x\); \(f'(x) = 0\) only when \(3x = \sqrt{x^2+4} \Rightarrow x = \frac{1}{\sqrt{2}}\). The endpoints are \(x = 0\) and \(x = 2\), so the critical numbers are \(x = 0\), \(x = \frac{1}{\sqrt{2}}\) and \(x = 2\): \(f\left(0\right) =6\), \(f\left(\frac{1}{\sqrt{2}}\right) \approx 5.66\) and \(f(2) \approx 6.49\), so \(f(x) = 3\sqrt{x^2+4}-x\) has a local max at \(x = 0\), a global and local min at \(x = \frac{1}{\sqrt{2}}\), and a global and local max at \(x = 2\).
37. \(f(x) = x^3 - \ln(x) \Rightarrow f'(x) = 3x^2 - \frac{1}{x}\), which exists for all \(x\) in the interval \(\left[\frac12, 2\right]\), and \(f'(x) = 0 \Rightarrow x = \frac{1}{\sqrt[3]{3}}\). The endpoints are \(x = \frac12\) and \(x = 2\), so the three critical numbers are \(x = \frac12\), \(x = \frac{1}{\sqrt[3]{3}}\) and \(x = 2\): \(f\left(\frac12\right) \approx 0.82\), \(f\left(\frac{1}{\sqrt[3]{3}}\right) \approx 0.70\) and \(f(2) \approx 7.3\) so \(f(x) = x^3 - \ln(x)\) has a local max at \(x = \frac12\), a global and local min at \(x = \frac{1}{\sqrt[3]{3}}\), and a global and local max at \(x = 2\).
39. \(A(x) = 4x\sqrt{1 - x^2}\) for \(0<x<1\), so:
    \begin{align*}A'(x) &= 4\left[\frac{-x^2}{\sqrt{1 - x^2}} + \sqrt{1 - x^2}\right]\\
    &= 4\left[\frac{1 - 2x^2}{\sqrt{1 - x^2}}\right]\end{align*}
    hence \(A'(x) > 0\) if \(0 < x < \frac{1}{\sqrt{2}}\) and \(A'(x) < 0\) if \(\frac{1}{\sqrt{2}} < x < 1\). Max when \(x = \frac{1}{\sqrt{2}}\): \(A\left(\frac{1}{\sqrt{2}}\right) = 2\)
41. \(V = x(8 - 2x)^2\) for \(0 \leq x \leq 4\), so: \begin{align*} V' &= x(2)(8 - 2x)(-2) + (8 - 2x)^2\\ &= (8 - 2x)( -4x + 8 - 2x)\\ &= (8 - 2x)(8 - 6x) = 4(4 - x)(4 - 3x)\end{align*} hence \(V ' < 0\) if \(x > \frac43\) and \(V' > 0\) if \(0 < x < \frac43\). \(V\left(\frac43\right) = \frac43 \left(8 - \frac83\right)^2 = \frac{1024}{27} \approx 37.926\) cubic units is the largest volume. Smallest volume is \(0\), which occurs when \(x = 0\) and \(x = 4\).
43. 1. \(4\): the endpoints and two values of \(x\) for which \(f'(x) = 0\)
    2. \(2\): the endpoints
    3. At most \(n + 1\): the two endpoints and the \(n - 1\) points \(x\) for which \(f'(x) = 0\); at least \(2\): the endpoints.
45. 1. local minimum at \((1,5)\)
    2. no extreme at \((1,5)\)
    3. local maximum at \((1,5)\)
    4. no extreme at \((1,5)\)
47. 1. \(0\), \(2\), \(6\), \(8\), \(11\), \(12\)
    2. \(0\), \(6\), \(11\)
    3. \(2\), \(8\), \(12\)
49. If \(f\) does not attain a maximum on \([a,b]\) or \(f\) does not attain a minimum on \([a,b]\), then \(f\) must have a discontinuity on \([a,b]\).
51. 1. yes, \(-1\)
    2. no
    3. yes, \(-1\)
    4. no
    5. yes, \(1 - \pi\)
53. 1. yes, \(0\)
    2. yes, \(0\)
    3. yes, \(0\)
    4. yes, \(0\)
    5. yes, \(0\)
55. 1. \(S(x)\) is minimum when \(x \approx 8\)
    2. \(S(x)\) is maximum when \(x = 2\).

Section 3.2

1. \(c \approx 3\), \(10\) and \(13\)
3. 1. \(\displaystyle c = \frac{\pi}{2}\)
   2. \(\displaystyle c = \frac{3\pi}{2}\), \(\displaystyle \frac{5\pi}{2}\), \(\displaystyle \frac{7\pi}{2}\), \(\displaystyle \frac{9\pi}{2}\)
5. Rolle’s Theorem asserts that the velocity \(h'(t)\) will equal \(0\) at some point between the time the ball is tossed and the time you catch it. The ball is not moving as fast when it reaches the balcony after being thrown from below.
7. The function does not violate Rolle&trsquo;s Theorem because the function does not satisfy the hypotheses of the theorem: \(f\) is not differentiable at \(0\), a point in the interval \(-1 < x < 1\).
9. No. Velocity is not the same as the rate of change of altitude, which is only one of the components of position. Rolle’s Theorem only says there was a time when altitude was not changing.
11. \(f'(x) = 3x^2 + 5\), so \(f'(x) = 0\) has no real roots. If \(f(x) = 0\) for a value of \(x\) other than \(2\), then by the corollary from Problem 10, we would have an immediate contradiction.
13. 1. \(f(0) = 0\), \( f(2) = 4\), \(f '(c) = 2c\), so \(\frac{4 - 0}{2 - 0} = 2c \Rightarrow c = 1\)
    2. \(f(1) = 4\), \(f(5) = 8\), \(f'(c) = 2c - 5\), so \(\frac{8 - 4}{5 - 1} = 2c - 5 \Rightarrow c = 3\)
15. 1. \(f(0) = 0\), \(f\left(\frac{\pi}{2}\right) = 1\), \(f'(c) = \cos(c)\), so \(\frac{1 - 0}{\frac{\pi}{2} - 0} = \cos(c) \Rightarrow c = \arccos\left(\frac{2}{\pi}\right) \approx 0.88\)
    2. \(f(-1) = -1\), \(f(3) = 27\), \(f'(c) = 3c^2\), so \(\frac{27 + 1}{3 + 1} = 3c^2 \Rightarrow c^2 = \frac73\), hence \(c = \sqrt{\frac73}\) (we know \(c > -1\), which eliminates \(c = -\sqrt{\frac73}\))
17. 1. \(f(1) = 4\), \(f(9) = 2\), \(f'(c) = \frac{-1}{2\sqrt{c}}\), so \(\frac{2 - 4}{1 - 9} = \frac{-1}{2\sqrt{c}} \Rightarrow -\frac14 = -\frac{1}{2\sqrt{c}} \Rightarrow c = 4\)
    2. \(f(1) = 3\), \(f(7) = 15\), \(f'(c) = 2\), so \(\frac{15 - 3}{7 - 1} = 2\) and any \(c\) between \(1\) and \(7\) will do.
19. The hypotheses are not all satisfied: \(f'(x)\) does not exist at \(x = 0\), which is between \(-1\) and \(3\).
21. \(f'(c) = 17\) at some time \(c\) does not prove the motorist “could not have been speeding.”
23. \(f(x) = x^3 + x^2 + 5x + c\), so \(f(1) = 7 + c = 10\) when \(c = 3\). Therefore \(f(x) = x^3 + x^2 + 5x + 3\).
25. 1. \(f'(x) = 2Ax\). We need \(A\cdot 1^2 + B = 9\) and \(2A\cdot 1 = 4\) so \(A = 2\) and \(B = 7\), hence \(f(x) = 2x^2 + 7\).
    2. \(A\cdot 2^2 + B = 3\) and \(2A\cdot 2 = -2\) so \(A = -\frac12\) and \(B = 5\), hence \(f(x) = -\frac12 x^2 + 5\).
    3. \(A\cdot 0^2 + B = 2\) and \(2A\cdot 0 = 3\), so there is no such \(A\). The point \((0,2)\) is not on the parabola \(y = x^2 + 3x - 2\).
27. \(f(x) = x^3 + C\), a family of “parallel” curves
29. \(v(t) = 300\): Assuming the rocket left the ground at \(t = 0\), we have \(y(1) = 300\) ft, \(y(2) = 600\) ft, \(y(5) = 1500\) ft.
31. \(f''(x) = 6\), \(f'(0) = 4\), \(f(0) = -5 \Rightarrow f(x) = 3x^2 + 4x - 5\)
33. 1. \(A(x) = 3x\)
    2. \(A'(x) = 3\)
35. 1. \(A(x) = x^2 + x\)
    2. \(A'(x) = 2x + 1\)
37. \(a_1 = 5\), \(a_2 = a_1 + 3 = 5 + 3 = 8\), \(a_3 = a_2 + 3 = (5 + 3) + 3 = 11\), \(a_4 = a_3 + 3 = (5+3 + 3) + 3 = 14\): in general, \(a_n = 5 + 3(n - 1) = 2 + 3n\)

Section 3.3

1. 
3. 
5. 
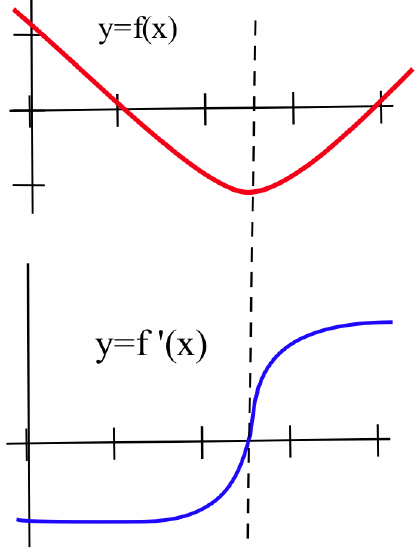
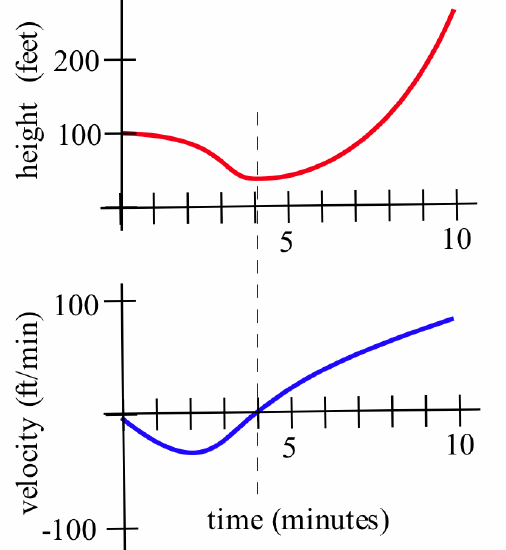
7. A: Q, B: P, C: R
9. \(f'(x) = \frac{1}{x} > 0\) for \(x > 0\) so \(f(x) = \ln(x)\) is increasing on \((0, \infty)\).
11. If \(f\) is increasing then \(f(1) < f(\pi)\) so \(f(1)\) and \(f(\pi)\) cannot both equal \(2\).
13. 1. \(x = 3\), \(x = 8\)
    2. maximum at \(x = 8\)
    3. none (or only at right endpoint)
14. Relative maximum height at \(x = 2\) and \(x = 7\); relative minimum height at \(x = 4\).
15. Relative maximum height at \(x = 6\); relative minimum height at \(x = 8\).
17. \(f(x) = x^3 - 3x^2 - 9x - 5\) has a relative minimum at \((3, -32)\) and a relative maximum at \((-1, 0)\).
19. \(h(x) = x^4 - 8x^2 + 3\) has a relative max at \((0, 3)\) and relative minimums at \((2, -13)\) and \((-2, -13)\).
21. \(r(t) = 2(t^2 + 1)^{-1}\) has a relative maximum at \((0, 2)\) and no relative minimums.
23. No positive roots. \(f(x) = 2x + \cos(x)\) is continuous and \(f(0) = 1 > 0\). Because \(f'(x) = 2 - \sin(x) \geq 1 > 0\) for all \(x\), \(f\) is increasing and never decreases back to the \(x\)-axis (a root).
24. One positive root. \(g(x) = 2x - \cos(x)\) is continuous, \(g(0) = -1 < 0\) and \(g(1) = 2 - \cos(1) \geq 1 > 0\) so by the Intermediate Value Theorem, \(g\) has a root between \(0\) and \(1\). Because \(g'(x) = 2 + \sin(x) \geq 1 > 0\) for all \(x\), g is always increasing and can have only that one root.
25. \(h(x) = x^3 + 9x - 10 \Rightarrow h'(x) = 3x^2 + 9 = 3(x^2 + 3) > 0\) for all \(x\) so \(h\) is always increasing and can cross the \(x\)-axis at most at one place. Because the \(h(1) = 0\), the graph of \(h\) crosses the \(x\)-axis at \(x = 1\), which is the only root of \(h\).
27. 1. See below left: \(f\) is always increasing but \(f'(1)\) is undefined.
       
    2. See above right: \(f(x) = x^3+1\) is always increasing but \(f'(0) =0\).
    3. If they travel at the same positive speed in different directions, then the distance between them will not remain constant.
29. 1. \(h(x) = x^2\) or \(x^2 + 1\) or \(x^2 - 7\) or, in general, \(x^2 + C\) for any constant \(C\).
    2. \(f(x) = x^2 + C\) and \(20 = f(3) = 3^2 + C \Rightarrow C = 20 - 9 = 11\) so \(f(x) = x^2 + 11\).
    3. \(g(x) = x^2 + C\) and \(7 = g(2) = 2^2 + C \Rightarrow C = 7 - 4 = 3\) so \(g(x) = x^2 + 3\).

Section 3.4

1. 1. \(f(t)\) = number of workers unemployed at time \(t\); \(f'(t) > 0\) and \(f''(t) < 0\)
   2. \(f(t)\) = profit at time \(t\); \(f'(t) < 0\) and \(f''(t) > 0\)
   3. \(f(t)\) = population at time \(t\); \(f'(t) > 0\) and \(f''(t) > 0\)
3. 
   4. Not possible.
5. 1. Concave up on \((0, 2)\), \((2, 3+)\), \((6, 9)\).
   2. Concave down on \((3+, 6)\). (A small technical note: we have defined concavity only at points where the function is differentiable, so we exclude the endpoints and points where the function is not differentiable from the intervals of concave up and concave down.)
7. \(g''(x) = 6x - 6 \Rightarrow g''(-1) < 0\) so \((-1, 12)\) is a local max; \(g''(3) > 0\) so \((3, -20)\) is a local min.
9. \(f''(x) = 5\left[-\sin^5(x) + 4\sin^3(x)\cdot \cos^2(x)\right] \Rightarrow f''\left(\frac{\pi}{2}\right) < 0\) so \(\left(\frac{\pi}{2}, 1\right)\) is a local maximum; \(f''\left(\frac{3\pi}{2}\right) > 0\) so \(\left(\frac{3\pi}{2}, -1\right)\) is a local minimum; \(f''(\pi) = 0\) and \(f\) changes concavity at \(x = \pi\) so \((\pi, 0)\) is an inflection point.
11. d and e
13. 1. \(0\)
    2. at most \(1\)
    3. at most \(n - 2\)

15. \(x\)	\(f(x)\)	\(f'(x)\)	\(f''(x)\)
    \(0\)	\(-\)	\(+\)	\(+\)
    \(1\)	\(+\)	\(0\)	\(-\)
    \(2\)	\(-\)	\(-\)	\(+\)
    \(3\)	\(0\)	\(+\)	\(+\)

17. 
19. \(f'(x) = 3x^2 - 42x + 144 = 3(x^2-14x+48)=3(x-6)(x-8)\), which exists everywhere and \(f'(x) = 0 \Rightarrow x = 6\) or \(x = 8\); meanwhile, \(f''(x) = 6x-42 = 6(x-7)\), so \(f''(6) = - 6 < 0\) means that \(f\) has a local max at \(x = 6\) and \(f''(8) = 6 > 0 \) means that \(f\) has a local min at \(x = 8\). The only candidate for an inflection point is where \(f''(x) = 0 \Rightarrow x = 7\); \(f''(x) < 0\) for \(x < 7\) and \(f''(x) > 0\) for \(x > 7\), so \(f\) does have an inflection point at \(x = 7\). A window with \(2 \leq x \leq 12\) and \(-50 \leq y \leq 10\) should work.
21. \(f'(x) = 7e^{7x} - 5 \Rightarrow f''(x) = 49e^{7x}\) so \(f''(x) > 0\) for all \(x\), hence \(f\) is always concave up and has no inflection points. Its only critical number is where \(7e^{7x} - 5 = 0 \Rightarrow e^{7x} = \frac57 \Rightarrow x = \frac17 \cdot \ln\left(\frac57\right) \approx -0.05\), which must be a local min. A window with \(-1 \leq x \leq \frac12\) and \(0 \leq y \leq 20\) should work.
23. \(f'(x) = -3e^{-3x} +1 \Rightarrow f''(x) = 9e^{-3x} > 0\) for all \(x\), hence \(f\) is always concave up and has no inflection points. Its only critical number: \(-3e^{-3x} +1 = 0 \Rightarrow e^{-3x} = \frac13 \Rightarrow x = \frac13 \cdot \ln\left(3\right) \approx 0.37\), which must be a local min. Try a window with \(-1 \leq x \leq 2\) and \(0 \leq y \leq 3\).
25. \(f'(x) = (1-3x)e^{-3x} \Rightarrow f''(x) = (9x-6)e^{-3x}\) so the only critical number is \(x = \frac13\) and \(f''\left(\frac13\right) -3e^{-1} < 0\), so it must be a local max. The only inflection point is where \(x = \frac23\). Try a window with \(-1 \leq x \leq 2\) and \(-2 \leq y \leq 1\).
27. \(f'(x) = \frac13 x^{-\frac23}\left(4x-1\right)\), so the critical numbers are \(x = 0\) and \(x = \frac14\); \(f''(x) = \frac29 x^{-\frac53}\left(2x+1\right)\) so the only candidates for an inflection point are \(x = 0\) and \(x = -\frac12\). Because \(f''(x) < 0\) when \(x < -\frac12\) and \(x >0\), the graph of \(f\) is concave up on those intervals and concave down for \(-\frac12 < x < 0\); because \(f\left(\frac14\right) > 0\), \(f\) has a local min at \(x = \frac14\). Try \(-1.5 \leq x \leq 2.5\) and \(-1 \leq y \leq 3\).
29. Critical number at \(x = 0\), which is a local min; inflection points at \(x = \pm 1\); concave up on \((-1,1)\), concave down elsewhere; try a window with \(-3 \leq x \leq 3\) and \(-1 \leq y \leq 3\).
31. Critical number at \(x = -1\), which is a local min; inflection points at \(x = -1\pm \sqrt{3}\); concave up between those values, concave down elsewhere; try a window with \(-6 \leq x \leq 6\) and \(-1 \leq y \leq 4\).

Section 3.5

1. 1. Using a rectangle with sides of length \(x\) and \(y\) as in the figure below:
      
      \(2x + 2y = 200 \Rightarrow y = 100 - x\). We want to maximize \(A = x\cdot y = x(100 - x) = 100x - x^2\) and \(A'(x) = 100 - 2x\) so \(A'(x) = 0 \Rightarrow x = 50 \Rightarrow y = 100 - x = 50\); \(A''(x) = - 2 < 0\) for all \(x\), so \(x = 50\) yields the maximum enclosed area. When \(x = 50\), \(A(50) = 50(100 - 50) = 2500\) square feet.
   2. Using a rectangle with sides of length \(x\) and \(y\) (see figure above) \(2x + 2y = P \Rightarrow y = \frac{P}{2} - x\). We want to maximize \(A = x\cdot y = x\left(\frac{P}{2} - x\right) = \left(\frac{P}{2}\right)x - x^2\) and \(A'(x) = \frac{P}{2} - 2x\) so \(A'(x) = 0\) when \(x = \frac{P}{4} \Rightarrow y = \frac{P}{2} - \frac{P}{4} = \frac{P}{4}\); \(A''(x) = -2 < 0\) for all \(x\), so \(x = \frac{P}{4}\) yields the maximum enclosed area. This garden is a \(\frac{P}{4}\) by \(\frac{P}{4}\) square.
   3. Using a rectangle with sides of length \(x\) and \(y,\) as in the figure below:
      
      \(2x + y = P \Rightarrow y = P - 2x\). We want to maximize \(A = xy = x(P - 2x) = Px - 2x^2\) and \(A'(x) = P - 4x\) so \(A'(x) = 0\) when \(x = \frac{P}{4} \Rightarrow y = P - 2\left(\frac{P}{4}\right) = \frac{P}{2}\).
   4. A circle. A semicircle.
3. 1. If \(x\) is the horizontal length and \(y\) is the vertical length, then \(120 = 2x + 5y \Rightarrow y = 24 - \frac25 x\). We want to maximize \(A = xy = x\left(24 - \frac25 x\right) = 24x - \frac25 x^2\) and \(A'(x) = 24 - \frac45 x\) so \(A'(x) = 0\) when \(x = 30\) (and \(y = 12\)); \(A''(x) = -\frac45 < 0\) for all \(x\) so \(x = 30\) yields the maximum enclosed area. Area is \((30\,\mbox{ft})(12\,\mbox{ft}) = 360\) square feet.
   2. A circular pen divided into four equal stalls by two diameters:
      
      does a better job than a square with area \(400\) square feet. If the radius is \(r\), then \(4r + 2\pi r = 120 \Rightarrow r = \frac{120}{4 + 2\pi} \approx 11.67\); the resulting enclosed area is \(A = \pi r^2 \approx \pi(11.67)^2 \approx 427.8\) square feet. The pen shown here:
      
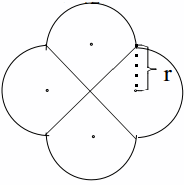
      does even better. If each semicircle has radius \(r\), then the figure uses \(4\sqrt{2}r + 4\pi r = 120\) feet of fencing so \(r = \frac{120}{4\sqrt{2} + 4\pi} \approx 6.585\) feet; the resulting enclosed area is \begin{align*}
      A &= (\mbox{square}) + (\mbox{four semicircles})\\
        &= (2r)^2 + 4\left(\frac12 \pi r^2\right) \approx 445.90\,\mbox{ft}^2\\
      \end{align*}
5. The dimensions of the bottom of the box are \(10-2x\) and \(5-x\) so we want to maximize \(V(x) = x(10 - 2x)(5 - x) = 50x - 20x^2 + 2x^3\); \(V'(x) = 50 - 40x + 6x^2 = 2(3x - 5)(x - 5)\) so \(V'(x) = 0\) when \(x = 5\) or \(x = \frac53\). When \(x = 5\), then \(V = 0\) (clearly not a maximum!) so \(x = \frac53\). The dimensions of the box with the largest volume are \(\frac53\) inches by \(\frac{10}{3}\) inches by \(\frac{20}{3}\) inches.
7. 1. Let \(r\) and \(h\) be the radius and height of the cylindrical can, so the volume is \(V = \pi r^2 h = 100 \Rightarrow h = \frac{100}{\pi r^2}\). We want to minimize the cost: \begin{align*}C &= 2(\mbox{top area}) + 5(\mbox{bottom area}) + 3(\mbox{side area})\\ &= 2\left(\pi r^2\right) + 5\left(\pi r^2\right) + 3\left(2\pi rh\right)\\ &= 7\pi r^2 + 6\pi r\left(\frac{100}{\pi r^2}\right) = 7\pi r^2 + \frac{600}{r}\end{align*} So \(C'(r) = 14\pi r - \frac{600}{r^2} \Rightarrow C'(r) = 0\) when \(r = \sqrt[3]{\frac{600}{14\pi}} \approx 2.39 \Rightarrow h \approx \frac{100}{\pi (2.39)^2} \approx 5.57\).
   2. Let \(k =\) top material cost \(+\) bottom material cost = 2¢ \(+\) bottom cost \(>\) 2¢ \(+\) 5¢ \(=\) 7¢. We want to minimize the cost \(C = k\pi r^2 + \frac{600}{r}\); \(C'(r) = 2k\pi r - \frac{600}{r^2}\) so \(C'(r) = 0\) when \(r = \sqrt[3]{\frac{600}{2k\pi}}\). If \(k = 8\), then \(r \approx 2.29\); if \(k = 9\), then \(r \approx 2.20\); if \(k = 10\), then \(r \approx 2.12\). As the cost of the bottom material increases, the radius of the least expensive cylindrical can decreases: the least expensive can becomes narrower and taller.
9. Recall that time \(= \frac{\mbox{distance}}{\mbox{rate}}\). Let the run distance \(= x\) (so \(0 \leq x \leq 60\); why?), hence the run time \(= \frac{x}{8}\) and the swim distance \(= \sqrt{40^2 + (60-x)^2}\) so the swim time \(= \frac12\sqrt{40^2 + (60-x)^2}\) and the total time is \(T(x) = \frac{x}{8} + \frac12\sqrt{40^2 + (60-x)^2}\). Differentiating to compute \(T'(x)\) yields: \begin{align*} \frac18 + \frac12 \cdot \frac12 \left(40^2 + (60-x)^2\right)^{-\frac12} \cdot 2(60 - x)(-1)\\ \qquad = \frac18 - \frac{60 - x}{2\sqrt{40^2 + (60-x)^2}}\end{align*} so \(T'(x) = 0\) when \(x = 60 \pm \frac{40}{\sqrt{15}}\). The value \(x = 60 + \frac{40}{\sqrt{15}} > 60\) so the least total time occurs when \(x = 60 - \frac{40}{\sqrt{15}} \approx 49.7\) meters. In this situation, the lifeguard should run about \(\frac56\) of the way along the beach before going into the water.
11. 1. Consider a similar problem with a new town \(D^*\) located at the “mirror image” of \(D\) across the river (below left):
       
       If the water works is built at any location \(W\) along the river, then the distances are the same from \(W\) to \(D\) and from \(W\) to \(D^*\): \(\mbox{dist}(W,D) = \mbox{dist}(W,D^*)\). Then \(\mbox{dist}(C,W) + \mbox{dist}(W,D) = \mbox{dist}(C,W) + \mbox{dist}(W,D^*)\) so the shortest distance from \(C\) to \(D^*\) is a straight line (see figure above right), and this straight line yields similar triangles with equal side ratios: \(\frac{x}{3} = \frac{10 - x}{5} \Rightarrow x = \frac{15}{4} = 3.75\) miles. A consequence of this “mirror image” view of the problem is that “at the best location \(W\) the angle of incidence \(\alpha\) equals the angle of reflection \(\beta\).”
    2. We want to minimize the cost: \begin{align*}C(x) &= 3000\mbox{dist}(C,W) + 7000\mbox{dist}(W,D)\\ &= 3000 \sqrt{x^2+9} + 7000\sqrt{(10 - x)^2 + 25}\end{align*} so, differentiating gives:\[C'(x) = \frac{3000x}{\sqrt{x^2 + 9}} + \frac{-7000(10 - x)}{\sqrt{(10 - x)^2 + 25}}\nonumber\]and (after much algebra) it turns out that \(C'(x) = 0\) when \(x \approx 7.82\) miles. As it becomes more expensive to build the pipe from \(W\) to \(D\), the cheapest route tends to shorten the distance from \(W\) to \(D\).
13. 1. Let \(x\) be the length of one edge of the square end. The volume is \(V(x) = x^2(108 - 4x) = 108x^2 - 4x^3 \Rightarrow V'(x) = 216x - 12x^2 = 6x(18 - x)\) so \(V'(x) = 0\) when \(x = 0\) or \(x = 18\). Clearly \(x=0\) results in a box of no volume, so the dimensions of the acceptable box with a square end and greatest volume are 18 in by 18 in by 36 in; the volume is 11,664 in\(^3\).
    2. Let \(x\) be the length of the shorter edge of the end. The volume \(V(x) = 2x^2(108 - 6x) = 216x^2 - 12x^3 \Rightarrow V'(x) = 432x - 36x^2 = 36x(12 - x)\) so \(V'(x) = 0\) if \(x = 0\) or \(x = 12\). Clearly \(x=0\) results in a box of no volume, so the dimensions of the box with an acceptable shape and largest volume are 12 in by 24 in by 36 in; the volume is 10,368 in\(^3\).
    3. Let \(x\) be the radius of the circular end. The volume is \(V(x) = \pi x^2(108 - 2\pi x) = 108\pi x^2 - 2\pi^2 x^3 \Rightarrow V'(x) = 216\pi x - 6\pi^2 x^2 = 6\pi x(36 - \pi x)\) so \(V'(x) = 0\) when \(x = 0\) or \(x = \frac{36}{\pi} \approx 11.46\) in. The dimensions of the acceptable box with circular end and largest volume are a radius of 11.46 in and a length of 36 in; the volume is 14,851 in\(^3\).
15. Without calculus: The area of the triangle is \(\frac12 (\mbox{base})(\mbox{height}) = \frac12 (7)(\mbox{height})\) and the height is maximum when the angle between the sides is a right angle.
    Using calculus: Let \(\theta\) be the angle between the sides. Then the area of the triangle is \(A = \frac72(10\sin(\theta)) = 35\sin(\theta) \Rightarrow A'(\theta) = 35\cos(\theta)\) so \(A'(\theta) = 0\) when \(\theta =\frac{\pi}{2}\), hence the triangle is a right triangle with sides 7 and 10.
    Using either approach, the maximum area of the triangle is \(\frac12 (7)(10) = 35\) square inches, and the third side is the hypotenuse with length \(\sqrt{7^2 + 10^2} = \sqrt{149} \approx 12.2\) inches.
17. 1. \(A(x) = 2x(16 - x^2) = 32x - 2x^3 \Rightarrow A'(x) = 32 - 6x^2\) so \(A'(c) = 0\) when \(x = \frac{32}{6} = \frac{16}{3} \approx 2.31\). The dimensions of the rectangle are \(2\left(\frac{16}{3}\right) \approx 4.62\) and \(16 - \left(\frac{16}{3}\right)^2 = \frac{32}{3} \approx 10.67\).
    2. \(A(x) = 2x\sqrt{1 - x^2}\) so, using the Product Rule:\[A'(x) = 2\left(\sqrt{1 - x^2} - \frac{x^2}{\sqrt{1 - x^2}}\right)\nonumber\]and \(A'(x) = 0\) when \(x = \frac{1}{\sqrt{2}} \approx 0.707\). The dimensions of the rectangle are \(2\left( \frac{1}{\sqrt{2}}\right) = \sqrt{2} \approx 1.414\) and \(\sqrt{1-\left(\frac{1}{\sqrt{2}}\right)^2} = \frac{1}{\sqrt{2}} \approx 0.707\).
    3. The graph of \(\left|x\right| + \left|y\right| = 1\) is a “diamond” (a square) with corners at \((1,0)\), \((0,1)\), \((-1,0)\) and \((0,-1)\). For \(0 \leq x \leq 1\):\[A(x) = 2x\cdot 2(1 - x) = 4x - 4x^2\nonumber\]so \(A'(x) = 4 - 8x\) and \(A'(x) = 0\) when \(x = \frac12\); \(A"(x) = - 8 < 0\) for all \(x\), so \(x = \frac12\) must be a local max. The dimensions of the rectangle are \(2\left(\frac12\right) = 1\) and \(2\left(1 - \frac12\right) = 1\).
    4. \(A(x) = 2x\cos(x)\), where \(0 \leq x \leq \frac{\pi}{2}\), so \(A'(x) = 2\cos(x) - 2x\cdot sin(x)\) and \(A'(x) = 0\) when \(x \approx 0.86\). The dimensions of the rectangle are \(2(0.86) = 1.72\) and \(\cos(0.86) \approx 0.65\).
19. The cross-sectional area is: \begin{align*}A &= 6\sin\left(\frac{\theta}{2}\right)\cdot 6\cos\left(\frac{\theta}{2}\right)\\ &= 36\cdot \frac12\sin(\theta) = 18\sin(\theta)\end{align*} which is a maximum when \(\theta = \frac{\pi}{2}\). Then the maximum area is \(A = 18\sin\left(\frac{\pi}{2}\right) = 18\) in\(^2\). (This problem is similar to Problem 15.)
21. \(V = \frac13 \pi r^2 h\) and \(h = \sqrt{9 - r^2}\) so:\[V(r) = \frac13 \pi r^2\sqrt{9 - r^2} = \frac{\pi}{3}\sqrt{9r^4 - r^6}\nonumber\]Differentiating and simplifying:\[V'(r) = \frac{\pi}{6} \cdot \frac{36r^3 - 6r^5}{\sqrt{9r^4 -r^6}}\nonumber\]so \(V'(r) = 0\) when \(36r^3 - 6r^5 = 6r^3(6-r^2)=0\); \(r=0\) results in zero volume, so \(r = \sqrt{6} \approx 2.45\) in \(\Rightarrow h = \sqrt{9 - (\sqrt{6})^2} = \sqrt3 \approx 1.73\) in.
23. Let \(n \geq 10\) be the number of passengers. The income is \(I(n) = n(30 - (n-10)) = 40n - n^2\) and the cost is \(C(n) = 100 + 6n\), so the profit is \(P(n) = I(n)- C(n) = (40n - n^2) - (100 + 6n) = 34n - n^2 - 100 \Rightarrow P'(n) = 34 - 2n\) so \(P'(n) = 0\) when \(n = 17\): 17 passengers on the flight maximize your profit. (This is an example of treating a naturally discrete variable, the number of passengers, as a continuous variable.)
25. Apply Problem 24 with \(R = f\) and \(E = g\).
27. 1. Let \(D\) be diameter of the can's base and \(H\) = the can's height. Then: \begin{align*}\theta &= \arctan\left(\frac{\mbox{radius of can}}{\mbox{height of CG}}\right)\\ &= \arctan\left(\frac{D/2}{H/2}\right) = \arctan\left(\frac{D}{H}\right)\end{align*} For this can, \(D = 5\) cm and \(H = 12\) cm so \(\theta = \arctan\left(\frac{2.5}{6}\right) \approx 0.395\) radians. The can can be tilted about \(22.6^{\circ}\) before it falls over.
    2. Differentiating \(C(x)\) yields:\[\frac{(60 + 19.2x)(19.2x) - (360 + 9.6x^2)(19.2)}{(60 + 19.2x)^2}\nonumber\]so \(C'(x) = 0 \Rightarrow (19.2)(9.6x^2+ 60x - 360 )= 0\) \(\Rightarrow x = 3.75\) or \(x=-10\): the height of the cola is \(3.75\) cm.
    3. \(C(3.75) = 3.75\) (The center of gravity is exactly at the top edge of the cola. It turns out that when the CG of a can-and-liquid system is as low as possible then the CG is at the top edge of the liquid.) Then \(\theta = \arctan\left(\frac{2.5}{3.75}\right) \approx 0.588\) radians: in this situation, the can can be tilted about \(33.7^{\circ}\) before it falls over.
    4. Less far.
29. \(A=(\mbox{base})(\mbox{height})= (1-x)(x^2) = x^2 - x^3\) for \(0 \leq x \leq 1\), so \(A'(x) =2x -3x^2\) and \(A'(x) = 0 \Rightarrow x = \frac23\) (clearly the endpoints \(x=0\) and \(x=1\) will not yield the largest area). So \(A\left(\frac23\right) = \frac13\left(\frac23\right)^2 = \frac{4}{27}\).
30. 1. \(A(x)= (1-x)(Cx^2) =Cx^2 - Cx^3\) where \(0 \leq x \leq 1\), so \(A'(x) =2Cx-3Cx^2\) and \(A'(x) = 0\) if \(x= \frac23\) (as before, neither endpoint works). So \(A\left(\frac23\right) = \frac13\cdot C\left(\frac23\right)^2 = \frac{4C}{27}\).
    2. \(A(x)= (B-x)(Cx^2) = BCx^2 - Cx^3\), where \(0 \leq x \leq B\), so \(A'(x) = 2BCx-3Cx^2 = Cx(2B-3x)\) and \(A'(x) = 0\) if \(x= \frac23 B\). So \(A\left(\frac{2B}{C}\right)= \left(\frac{B}{3}\right)(C)\left(\frac{2B}{3}\right)^2 = \frac{4}{27}B^3 C\).
31. 1. Position the lower-left vertex of the triangle at \((0,0)\) so the hypotenuse sits on \(y =20-\frac{20}{50}x\) and the area of the rectangle is \(A= xy = x\left(20- \frac25 x\right) = 20x - \frac25 x^2 \Rightarrow A'(x) = 20 - \frac45 x\) and \(A'(x) = 0\) when \(x = 25\). Then \(y=10\) and the area of the rectangle is \(25\cdot 10 = 250\).
    2. Proceeding as in part (a), \(y =H-\frac{H}{B}x\) and \(A(x) =x\left(H-\frac{H}{B}x\right) = Hx - \frac{H}{B}x^2 \Rightarrow A'(x) =H-\frac{2H}{B}x\) and \(A'(x) = 0\) when \(x = \frac{B}{2}\). Then \(y =\frac{H}{2}\) and area of rectangle is \(\frac{B}{2} \cdot \frac{H}{2} = \frac{BH}{4}\).
33. Let \(r\) and \(h\) be radius and height of can, and \(F = (\mbox{top cost})+(\mbox{bottom cost})+(\mbox{cost of sides})= A\left(\pi r\right)^2 + B\left(\pi r\right)^2+C(2\pi rh)\). But volume \(V = \pi r^2 h \Rightarrow h = \frac{V}{\pi r^2}\) so \(F(r) = (A+B)\pi r^2 + \frac{2CV}{r} \Rightarrow F'(r) 2(A+B)\pi r - \frac{2CV}{r^2}\), so \(F'(r) = 0\) when \(r = \sqrt[3]{\frac{CV}{\pi(A+B)}}\). Now you can find \(h\) and \(F\).

Section 3.6

1. 1. \(h(x)\) has a root at \(x = 1\).
   2. \(\displaystyle \lim_{x\rightarrow 1^{+}}\, h(x) = 0\), \(\displaystyle \lim_{x\rightarrow 1^{-}}\, h(x) = 0\)
      \(\displaystyle \lim_{x\rightarrow 3^{+}}\, h(x) = -\infty\), \(\displaystyle \lim_{x\rightarrow 3^{-}}\, h(x) = +\infty\)
   3. \(y = h(x)\) has a vertical asymptote at \(x = 3\)
3. \(\displaystyle \lim_{x\rightarrow 2^{+}}\, h(x) = +\infty\), \(\displaystyle \lim_{x\rightarrow 2^{-}}\, h(x) = -\infty\)
   \(\displaystyle \lim_{x\rightarrow 4^{+}}\, h(x) = 0\), \(\displaystyle \lim_{x\rightarrow 4^{-}}\, h(x) = 0\)
5. \(0\)
7. \(-3\)
9. \(0\)
11. DNE
13. \(\frac23\)
15. \(0\)
17. \(-7\)
19. \(3\)
21. \(\cos(0) = 1\)
23. \(\ln(1) = 0\)
25. 1. \(V(t) = 50 + 4t\) gals, \(A(t) = 0.8t\) lbs of salt
    2. \(C(t) = %\frac{\mbox{amount of salt}}{\mbox{total amount of liquid}} = \frac{A(t)}{V(t)} = \frac{0.8t}{50 + 4t}\)
    3. as \(t \rightarrow \infty\), \(C(t) \rightarrow \frac{0.8}{4} = 0.2\) lbs per gal
    4. \(V(t) = 200 + 4t\) and \(A(t) = 0.8t\), so \(C(t) = \frac{0.8t}{200 + 4t} \rightarrow \frac{0.8}{4} = 0.2\) lbs per gal
27. \(+\infty\)
29. \(-\infty\)
31. \(-\infty\)
33. \(-\infty\)
35. \(+\infty\)
37. \(-\infty\)
39. \(1\)
41. \(-\infty\)
43. horizontal: \(y = 0\); vertical: \(x = 0\)
44. horizontal: \(y = 0\); vertical: \(x = 0\); “hole”: \((1,1)\)
45. horizontal: \(y = 0\); vertical: \(x = 3\) and \(x = 1\)
47. vertical: \(x = -1\)
49. horizontal: \(y = 1\); vertical: \(x = 1\)
51. slant: \(y = 2x + 1\); vertical: \(x = 0\)
53. other: \(y = \sin(x)\); vertical: \(x = 2\)
55. other: \(y = x^2\)
57. other: \(y = \cos(x)\); vertical: \(x = 3\)
59. \(y = \sqrt{x}\); \(x = -3\)

Section 3.7

1. \(\displaystyle \lim_{x\to 1}\, \frac{x^3-1}{x^2-1} = \lim_{x\to 1}\, \frac{3x^2}{2x} =\lim_{x\to 1}\, \frac32 x = \frac32\)
3. \(\displaystyle \lim_{x\to 0}\, \frac{\ln(1+3x)}{5x} = \lim_{x\to 0}\, \frac{\frac{3}{1+3x}}{5} = \frac35 \)
5. \(\displaystyle \lim_{x\to 0}\, \frac{x\cdot e^x}{1-e^x} = \lim_{x\to 0}\, \frac{x\cdot e^x + e^x \cdot 1}{-e^x} = \lim_{x\to 0}\, \frac{x+1}{-1} = -1\)
7. \(\displaystyle \lim_{x\to \infty}\, \frac{\ln(x)}{x} = \lim_{x\to \infty}\, \frac{\frac{1}{x}}{1} = 0\)
9. \(\displaystyle \lim_{x\to \infty}\, \frac{\ln(x)}{x^p} = \lim_{x\to \infty}\, \frac{\frac{1}{x}}{px^{p-1}} = \lim_{x\to \infty}\, \frac{1}{px^p} = 0\)
11. \(\displaystyle \lim_{x\to 0}\, \frac{1-\cos(3x)}{x^2} = \lim_{x\to 0}\, \frac{3\sin(3x)}{2x}= \lim_{x\to 0}\, \frac{9\cos(3x)}{2} =\frac92\)
13. For \(a \neq 0\): \(\displaystyle \frac{f'}{g'} = \frac{m}{n}x^{m-n} \rightarrow \frac{m}{n}a^{m-n}\). For \(a=0\):\[\lim_{x\to a}\, \frac{x^m - a^m}{x^n - a^n} = \left\{\begin{array}{rl} { 0 } & { \text{if } m > n } \\ { 1 } & { \text{if } m = n } \\ {+\infty } & { \text{if } m < n \text{ and } (m-n) \text{ is even} } \\ {\text{DNE} } & { \text{if } m < n \text{ and } (m-n) \text{ is odd} } \end{array}\right.\nonumber\]
15. \(\displaystyle \lim_{x\to 0}\, \frac{1-\cos(x)}{x\cdot \cos(x)} = \lim_{x\to 0}\, \frac{\sin(x)}{-x\cdot\sin(x) + \cos(x)}= 0\)
17. \(\displaystyle \frac{f'}{g'} = \frac{pe^{px}}{3} \rightarrow \frac{p}{3}\) so \(p = 3(5) = 15\).
19. 1. All three limits are \(+\infty\).
    2. After applying L’Hôpital’s Rule \(m\) times: \begin{align*} \frac{f^{(m)}}{g^{(m)}} &= \frac{a\cdot b^m \cdot e^{bn}}{c(m)(m-1)(m-2)\cdots (2)(1)}\\ &= \frac{\mbox{constant}\cdot e^{bn}}{\mbox{another constant}} \rightarrow +\infty \end{align*}
21. \(\displaystyle \lim_{x\to 0^{+}}\, \frac{\ln(x)}{\csc(x)} = \lim_{x\to 0^{+}}\, \frac{-\sin(x)}{x}\cdot \tan(x) = -1\cdot 0 = 0\)
23. \(\displaystyle \lim_{x\to 0^{+}}\, \frac{\ln(x)}{x^{-\frac12}} = \lim_{x\to 0^{+}}\, \frac{\frac{1}{x}}{-\frac12 x^{-\frac32}} = \lim_{x\to 0^{+}}\, -2\sqrt{x} = 0\)
25. Write \(\displaystyle \left(1-\frac{3}{x^2}\right)^x = e^{x\cdot\ln\left(1-\frac{3}{x^2}\right)}\) and compute:\[\lim_{x\to \infty}\, \frac{\ln\left(1-\frac{3}{x^2}\right)}{\frac{1}{x}} = \lim_{x\to \infty}\, \frac{-6}{x-\frac{3}{x}} = 0\nonumber\]so that the original limit equals \(e^0 = 1\).
27. \(\displaystyle \lim_{x\to 0}\, \frac{\sin(x)-x}{x\cdot\sin(x)} = \lim_{x\to 0}\, \frac{\cos(x)-1}{x\cdot\cos(x)+\sin(x)}\) \[\mbox{ } \qquad \qquad \qquad \ \, = \lim_{x\to 0}\, \frac{-\sin(x)}{-x\cdot\sin(x)+2\cos(x)} = 0\nonumber\]
29. Write \(\displaystyle \left(\frac{x+5}{x}\right)^\frac{1}{x} = e^{\frac{\ln\left(\frac{x+5}{x}\right)}{x}}\) and compute:\[\lim_{x\to \infty}\, \frac{\ln\left(\frac{x+5}{x}\right)}{x} = \lim_{x\to \infty}\, \frac{-5}{x(x+5)} = 0\nonumber\]so that the original limit equals \(e^0 = 1\).