4.0: Area

Last updated
Save as PDF

Page ID: 212031

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\dsum}{\displaystyle\sum\limits} $

$ \newcommand{\dint}{\displaystyle\int\limits} $

$ \newcommand{\dlim}{\displaystyle\lim\limits} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

The primary purpose of this introductory section is to help develop your intuition about areas and your ability to reason using geometric arguments about area. This type of reasoning will appear often in the rest of this book and is very helpful for applying the ideas of calculus.

The basic shape we will use is the rectangle: the area of a rectangle is $(\mbox{base})\cdot(\mbox{height})$. If the units for each side of the rectangle are “meters,” then the area will have units $(\mbox{meters})\cdot(\mbox{meters}) =$ “square meters” $= \mbox{m}^2$. The only other area formulas needed for this section are for triangles (area $= \frac12 b\cdot h$) and for circles (area $= \pi\cdot r^2$). In addition, we will use (and assume to be true) three other familiar properties of area:

Addition Property: The total area of a region is the sum of the areas of the non-overlapping pieces that comprise the region:
$On the left of an = sign is a solid region shaded orange consisting of a right triangle abutting a rectangle of the same height abutting a half-disk with a diameter that matches the height of the rectangle; dashed vertical line segments separate the three types of figures. On the right of the equal sign are the three figured separated, with a + sign between each pair.$
Inclusion Property: If region $B$ is inside region $A$ (see margin), then the area of region $B$ is less than or equal to the area of region $A$:
$A mathematical diagram showing a blue curve in the first quadrant of a coordinate plane. The area between the curve and the x and y axes is shaded with light blue diagonal lines and labeled with a large letter "A". Inside this region, a rectangle is drawn with its bottom-left corner at the origin and its top-right corner touching the blue curve. This rectangle is shaded with a cross-hatch pattern and labeled with a large letter "B".$
Location-Independence Property: The area of a region does not depend on its location:
$The image displays three yellow rectangles to demonstrate that area is independent of orientation. Each rectangle is composed of a grid of six smaller squares. The first rectangle is rotated diagonally with a side of length 3 and a base of length 2. The second rectangle stands vertically with a height of 3 and a base of 2. The third rectangle lies horizontally with a height of 2 and a base of 3.$

Example $\PageIndex{1}$

Determine the area of the region shown below left.

$On the left, there is a single six-sided polygon. The top horizontal side is labeled 5, the far left vertical side is labeled 7, and a smaller notched section on the right has a horizontal side labeled 1 and a vertical side labeled 3. On the right, the same shape is shown split into two separate rectangles. The larger rectangle has a height of 7 and a top width of 5. Next to it is a smaller, thinner rectangle with a height of 3 and a top width of 1.$

Solution

We can easily break the region into two rectangles (shown above right), with areas of $35$ square inches and $3$ square inches respectively, so the area of the original region is $38$ square inches.

Practice $\PageIndex{1}$

Determine the area of the trapezoidal region shown below:

$The image shows a light green trapezoid with a black outline. The left vertical side is labeled 3. The top horizontal side is labeled 6. The bottom horizontal side is longer and labeled 10. The right side is a slanted line labeled 5.$

by cutting it in two ways:

into a rectangle and triangle and
into two triangles.

Answer

$3(6) + \frac12(4)(3) = 24$
$\frac12 (3)(10) + \frac12 (6)(3) = 24$

We can use our three area properties to deduce information about areas that are difficult to calculate exactly. Let $A$ be the region bounded by the graph of $\displaystyle f(x) = \frac{1}{x}$, the $x$-axis, and the vertical lines $x = 1$ and $x = 3$. Because the two rectangles in the margin figure sit inside region $A$ and do not overlap each other, the area of the rectangles, $\displaystyle \frac12 + \frac13 = \frac56$, is less than the area of region $A$.

Practice $\PageIndex{2}$

Build two rectangles, each with base $1$ unit, with boundaries that extend outside the shaded region in the figure below:

$A graph of f(x) = 1/x in the first quadrant with the region below the curve and above the x-axis between x=1 and x=3 shaded orange. Two rectangles sit inside the orange shaded region: the first has corners at (1,0), (2,0), (2,0.5) and (1,0.5), the second at (2,0), (3,0), (3,1/3) and (2,1/3). An arrow points to the shaded region with the label 'Region A.'$

and use their areas to make another valid statement about the area of region $A$.

Answer: outside rectangular area $= (1)(1) + (1)\left(\frac12\right) = 1.5$

Practice $\PageIndex{3}$

What can you say about the area of region $A$ from Practice $\PageIndex{2}$ if we use “inside” and “outside” rectangles each with base $\frac12$ unit?

Answer: Using rectangles with base $= \frac12$:
\begin{align*}\mbox{inside area} &= \frac12\left(\frac23 + \frac12 + \frac25 + \frac13\right) = \frac{57}{60} \approx 0.95\\
\mbox{outside area} &= \frac12\left( 1 + \frac23 + \frac12 + \frac25\right) = \frac{72}{60} = 1.2\end{align*}
so the area of the region is between $0.95$ and $1.2$.

Example $\PageIndex{2}$

The figure below right includes 32 dark squares, each 1 centimeter on a side, and 31 lighter squares of the same size:

$On the left, there is a large, yellow irregular shape labeled leaf with a black outline. On the right, the same leaf shape is placed over a coordinate grid. To estimate its area, squares from the grid are highlighted in two different ways: squares that are entirely contained within the leaf's boundary are filled with a dense pattern of blue and red dots; squares that are only partially covered by the leaf are filled with a sparse pattern of black dots.$

We can be sure that the area of the leaf below left is smaller than what number?

Solution

The area of the leaf is smaller than $32 + 31 = 63\, \mbox{cm}^2$.

Practice $\PageIndex{4}$

We can be sure that the area of the leaf from Example $\PageIndex{2}$ is at least how large?

Answer: The leaf’s area is larger than the area of the dark rectangles, $32\,\mbox{cm}^2$.

Functions can be defined in terms of areas. For the constant function $f(t) = 2$, define $A(x)$ to be the area of the rectangular region:

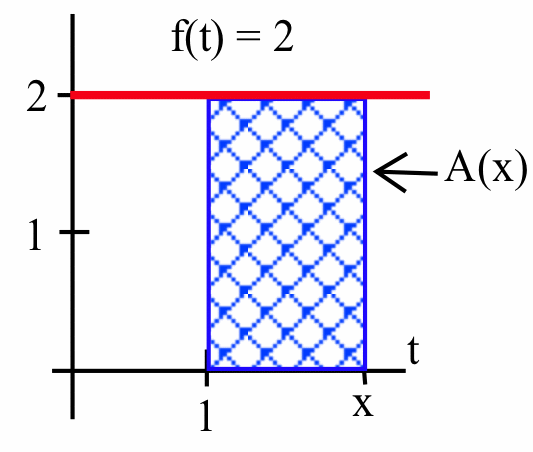
$A graph of the horizontal line f(t) = 2 in the first quadrant, with a blue-shaded rectangle below this line, above the t-axis and between t=1 and t=x. An arrow labels the rectangle as A(x).$

bounded by the graph of $f$, the $t$-axis, and the vertical lines at $t=1$ and $t=x$; we can easily see that $A(2) = 2$, as indicated by the shaded region:

$A graph of the horizontal line f(t) = 2 in the first quadrant, with a blue-shaded rectangle below this line, above the t-axis and between t=1 and t=2. An arrow labels the rectangle as A(2)=2.$

Similarly, $A(3)= 4$ and $A(4)=6$. In general, $A(x)= (\mbox{base})(\mbox{height}) = (x-1)(2) = 2x - 2$ for any $x\geq 1$. From the graph of $y=A(x)$:

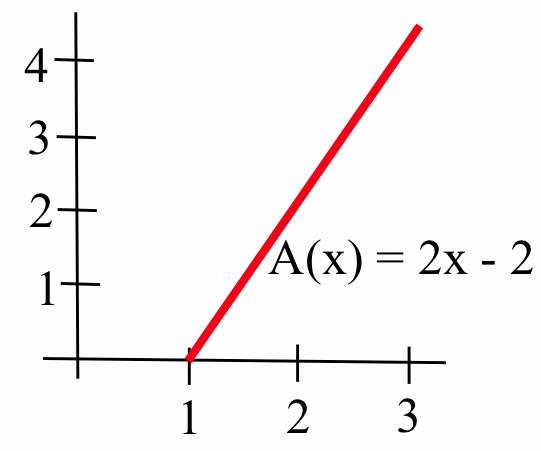
$A graph of the red half-line A(x) = 2x-2 in the first quadrant.$

we can see that $A'(x) = 2$ for every value of $x > 1$.

(The fact that $A'(x) = f(x)$ in the preceding discussion is not a coincidence, as we shall soon learn.)

Practice $\PageIndex{5}$

For $f(t)=2$, define $B(x)$ to be the area of the region bounded by the graph of $f$, the $t$-axis, and vertical lines at $t = 0$ and $t = x$:

$A graph of the horizontal line f(t) = 2 in the first quadrant, with a blue-shaded rectangle below this line, above the t-axis and between t=0 and t=x. An arrow labels the rectangle as B(x).$

Fill in the table below with the requested values of $B$. How are the graphs of $y = A(x)$ and $y = B(x)$ related?

$x$	$B(x)$
$0$
$0.5$
$1$
$2$

Answer

$y = B(x) = 2x$ is a line with slope $2$, so it is parallel to the line $y = A(x) = 2x - 2$.

$x$	$B(x)$
$0$	$0$
$0.5$	$1$
$1$	$2$
$2$	$4$

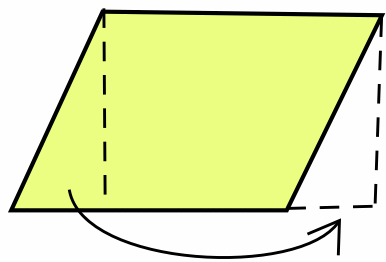
Sometimes it is useful to move regions around. The area of a parallelogram is obvious if we move the triangular region from one side of the parallelogram to fill the region on the other side, resulting in with a rectangle:

$A yellow parallelogram with a black outline. A vertical dashed line is drawn from the top-left vertex down to the base, forming a right triangle on the left side of the shape. An arrow at the bottom points from this left-hand triangle toward the right side of the parallelogram. On the right side, a matching triangle is outlined with dashed lines, showing that if the triangle from the left is moved to the right, the entire shape becomes a rectangle.$

At first glance, it is difficult to estimate the total area of the shaded regions shown below left:

$On the left, a red curve is plotted on a coordinate grid with horizontal dashed lines at y = 1, y = 2, and y = 3, and vertical dashed lines at x = 1, x = 2, x = 3, and x = 4. Three blue-shaded regions are shown between the curve and the vertical grid lines, representing slices of the total area. Horizontal arrows point from these three blue regions toward the right side of the image. On the right, the three blue slices are stacked vertically into a single rectangular column that has a base width of 1 and a total height of 2.$

but if we slide all of them into a single column (above right), then becomes easy to determine that the shaded area is less than the area of the enclosing rectangle $= (\mbox{base})(\mbox{height}) = (1)(2) = 2$.

Practice $\PageIndex{6}$

The total area of the shaded regions in the figure below:

is less than what number?

Answer

Area $<$ area of the rectangle enclosing the shifted regions $= 5$:

$A red curve decreases from (0,5) to (4,0). Beneath the curve, are rectangles, separated by vertical dashed-black line segments, with upper-right vertices on the curve at x = 1, 2, 3, and 4 (the last of which has height 0). The region above these rectangles and below the curve is shaded blue. To the right, the four blue-shaded pieces from the left graph are stacked on top of each other, with double arrows indicating their width to be 1 and their collective heigh to be 5. A dashed-black horizontal line segment is at a height of 5 at the top of the picture and a vertical one is at the far right. Four arrows point from each of the four blue-shaded regions on the left to their counterparts on the right.$

Some Applications of “Area”

One reason “areas” are so useful is that they can represent quantities other than sizes of simple geometric shapes. For example, if the units of the base of a rectangle are “hours” and the units of the height are “$\frac{\mbox{miles}}{\mbox{hour}}$,” then the units of the “area” of the rectangle are:\[(\mbox{hours})\cdot\left(\frac{\mbox{miles}}{\mbox{hour}}\right) = \mbox{miles}\nonumber\]a measure of distance:

$A blue-shaded rectangle with vertices at (1,0), (3,0), (3,10) and (1,10). The horizontal axis has label 'time (hours)' and the vertical axis 'velocity (miles/hour).'$

Similarly, if the base units are “pounds” and the height units are “feet,” then the “area” units are “foot-pounds,” a measure of work.

In the figure below, $f(t)$ is the velocity of a car in “miles per hour,” and $t$ is the time in “hours”:

$A violet-shaded rectangle with vertices at (1,0), (4,0), (4,20) and (1,20) with the top labeled 'f(t)=20 mpg' and a dashed-black line segment connecting the upper-left corner to (0,20). The horizontal axis has tick marks labeled 1 pm, 2 pm, 3 pm and 4 pm, and the vertical axis 'velocity (miles/hour).'$

So the shaded “area” will be $(\mbox{base})\cdot(\mbox{height}) = (3\,\mbox{hours})\cdot\left(20\,\frac{\mbox{miles}}{\mbox{hour}}\right) = 60$ miles, the distance traveled by the car in the 3 hours from 1:00 p.m. until 4:00 p.m.

Distance as an “Area”

If $f(t)$ is the (positive) forward velocity of an object at time $t$, then the “area” between the graph of $f$ and the $t$-axis and the vertical lines at times $t = a$ and $t = b$ will equal the distance that the object has moved forward between times $a$ and $b$.

This “area as distance” concept can make some difficult distance problems much easier.

Example $\PageIndex{3}$

A car starts from rest (velocity $= 0$) and steadily speeds up so that 20 seconds later its speed is 88 feet per second (60 miles per hour). How far did the car travel during those 20 seconds?

Solution

We could answer the question using the techniques of Chapter 3 (try this). But if “steadily” means that the velocity increases linearly, then it is easier to use the figure below:

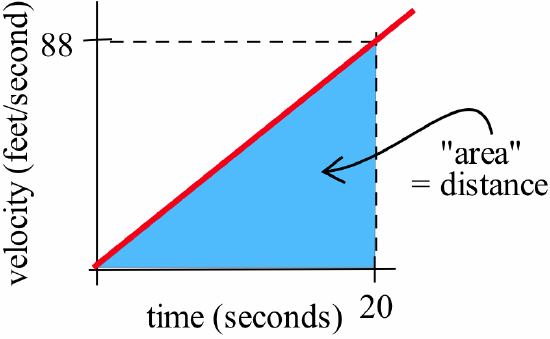
$A red half-line passes through (0,0) and (20,88) in the first quadrant with dashed-black lines connecting (20,88) to (0,88) and to (20,0). The triangular region below the red line and to the right of the vertical dashed segment is shaded blue and a curved arrrow points to this region with the label "area" = distance. The horizontal axis is labeled 'time (seconds)' and the vertical axis 'velocity (feet/second).'$

and the concept of “area as distance.”

The “area” of the triangular region represents the distance traveled:\[\mbox{distance} = \frac12 (\mbox{base})(\mbox{height}) = \frac12 (20\,\mbox{sec})\left(88\,\frac{\mbox{ft}}{\mbox{sec}}\right) = 880\,\mbox{ft}\nonumber\]The car travels a total of 880 feet during those 20 seconds.

Practice $\PageIndex{7}$

A train initially traveling at 45 miles per hour (66 feet per second) takes 60 seconds to decelerate to a complete stop. If the train slowed down at a steady rate (the velocity decreased linearly), how many feet did the train travel before coming to a stop?

Answer

Draw a graph of the velocity function:

$A red line segment passes through (0,66) and (60,0) in the first quadrant, with triangular region below the segment shaded yellow. A caption reads "area" = distance = 1980 ft. The horizontal axis is labeled 'time (seconds)' and the vertical axis 'velocity (feet/sec).'$

and then use the concept of “area as distance”:
\begin{align*}
\mbox{distance} &= \mbox{area of shaded region}\\
&= \frac12(\mbox{base})(\mbox{height})\\
&= \frac12(60\,\mbox{sec})\left(66\,\frac{\mbox{ft}}{\mbox{sec}}\right) = 1980\,\mbox{feet}\end{align*}

Practice $\PageIndex{8}$

You and a friend start off at noon and walk in the same direction along the same path at the rates shown below:

$A concave down, increasing red curve labeled 'You' and a blue curve labeled 'Friend' that begins concave up and transitions to concave down at 2 pm both start at the origin (where time is 12 pm and velocity is 0) and intersect at 2 pm, with the red curve above the blue to the left of a dashed-black vertical line at 2 pm and the blue curve aboe the red to the right of this dashed line. The horizontal axis has tick marks labeled 1 pm, 2 pm and 3 pm, and the vertical axis 'velocity.'$

Who is walking faster at 2:00 p.m.? Who is ahead at 2:00 p.m.?
Who is walking faster at 3:00 p.m.? Who is ahead at 3:00 p.m.?
When will you and your friend be together? (Answer in words.)

Answer

At 2:00 p.m. both are walking at the same velocity. You are ahead.
At 3:00 p.m. your friend is walking faster than you, but you are still ahead. (The “area” under your velocity curve is larger than the “area” under your friend’s.)
You and your friend will be together on the trail when the “areas” (distances) under the two velocity graphs are equal.

In the preceding Example and Practice problems, a function represented a rate of travel (in miles per hour, for instance) and the area represented the total distance traveled. For functions representing other rates, such as the production of a factory (bicycles per day) or the flow of water in a river (gallons per minute) or traffic over a bridge (cars per minute) or the spread of a disease (newly sick people per week), the area will still represent the total amount of something.

“Area” as a Total Accumulation

If $f(t)$ represents a positive rate (in units per time interval) at time $t$, then the “area” between the graph of $f$ and the $t$-axis and the vertical lines at times $t=a$ and $t=b$ will be the total amount of {something} that accumulates between times $a$ and $b$:

$A red curve labeled y=f(t) in the first quadrant, together with dashed-black vertical lines at t=a and t=b. The region below the red curve, above the horizontal t-axis and between the dashed lines is shaded green and labeled "area" = total accumulation. The horizontal axis is labeled 'time' and the vertical axis 'rate (units/time).'$

For example, the figure below shows the flow rate (in cubic feet per second) of water in the Skykomish River near the town of Gold Bar, Washington:

$The horizontal axis is labeled Month and shows letters representing the months of the year, from J for January through D for December. The vertical axis is labeled thousand cubic feet per second and has numerical markings for 2, 4, 6, and 8. A red curve represents the flow rate throughout the year. The curve begins near 4.5 in January and slopes slightly downward through April. It rises sharply to a peak of approximately 7.2 in late May or early June. It then drops to a low point of about 1 in September before rising again toward the end of the year. A single vertical blue rectangular region is highlighted under the curve during the month of October. This rectangle extends from the horizontal axis up to a height of about 3.5 thousand cubic feet per second, where its top right corner touches the red curve.$

The area of the shaded region represents the total volume (cubic feet) of water flowing past the town during the month of October:

\begin{align*}\mbox{total water} &= \mbox{“area”} = \mbox{area of rectangle} + \mbox{area of triangle}\\ &\approx \left(2000\,\frac{\mbox{ft}^3}{\mbox{sec}}\right)(30\,\mbox{days}) + \frac12\left(1500\,\frac{\mbox{ft}^3}{\mbox{sec}}\right)(30\,\mbox{days})\\ &= \left(2750\,\frac{\mbox{ft}^3}{\mbox{sec}}\right)(30\,\mbox{days}) = \left(2750\,\frac{\mbox{ft}^3}{\mbox{sec}}\right)(2592000\,\mbox{sec})\\ &\approx 7.128\times 10^9\,\mbox{ft}^3\end{align*}

For comparison, the flow over Niagara Falls is about $2.12\times 10^5\,\frac{\mbox{ft}^3}{\mbox{sec}}$.

Problems

1. Calculate the area of the shaded region:
  $fig400_19a.png$
2. Calculate the area of the shaded region:
  $A large cyan rectangle containing a smaller white rectangular cutout located in the lower right region. The outer cyan rectangle has a total horizontal width of 20 and a vertical height of 10. The inner white rectangle is defined by a width of 8 and a height of 3.$
Calculate the area of the trapezoidal region in the figure below left by breaking it into a triangle and a rectangle.
$Two yellow trapezoids side by side. The first, on the left, has a flat horizontal base with a length of 4. The left vertical side has a height of 4, while the right vertical side is taller with a height of 6. The top is a slanted line connecting these two different heights. The second trapezoid, on the right, shows the same geometric structure but the horizontal base is labeled B, the shorter left vertical side is labeled h, and the taller right vertical side is labeled H.$
Break the region shown above right into a triangle and rectangle and verify that the total area of the trapezoid is $\displaystyle b\cdot\left(\frac{h + H}{2}\right)$.
1. Calculate the sum of the rectangular areas in the region shown below left.
  $Two graphs of a red curve y=1+x^2 on a [0,2]X[0,6] grid. The graph on the left has two green-shaded rectangles of width 1 below the curve with their bases on the horizontal axis and their upper-left corners on the curve at (0,1) and (1,2). In the graph on the right, the region below the curve, above the horizontal axis and between x = 0 and x = 2 is shaded blue.$
2. What can you say about the area of the shaded region shown above right?
1. Calculate the sum of the areas of the rectangles shown below left.
  $Two graphs of a red curve y=4-2^x in the first quadrant. The graph on the left has two green-shaded rectangles of width 1 with their bases on the horizontal axis and their upper-left corners on the curve at (0,3) and (1,2). In the graph on the right, the region below the curve and above the horizontal axis is shaded green.$
2. What can you say about the area of the shaded region shown above right?
1. Calculate the sum of the areas of the trapezoids shown below left.
  $Two graphs of a red curve y=4-2^x in the first quadrant. The graph on the left has black line segments connecting (0,3) and (1,2), and (1,2) and (2,0); the region below these line segments and above the horizontal axis is shaded green. In the graph on the right, the region below the curve and above the horizontal axis is shaded green.$
2. What can you say about the area of the shaded region shown above right?
Consider the region bounded by the graph of $y = 2+x^3$, the positive $x$-axis, the positive $y$-axis and the line $x=2$. Use two well-placed rectangles to estimate the area of this region.
Consider the region bounded by the graph of $y = 9-3^x$, the positive $x$-axis and the positive $y$-axis. Use two well-placed trapezoids to estimate the area of this region.
Let $A(x)$ represent the area bounded by the graph of the function shown below, the horizontal axis, and vertical lines at $t=0$ and $t=x$:
$A red piecewise-linear curve connecting (0,1) to (1,1) to (2,2) to (3,2) to (4,1) to (5,1).$
Evaluate $A(x)$ for $x = 1$, $2$, $3$, $4$ and $5$.
Let $B(x)$ represent the area bounded by the graph of the function shown below, the horizontal axis, and vertical lines at $t=0$ and $t=x$:
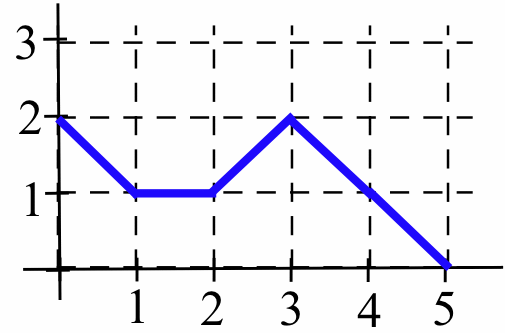
$A blue piecewise-linear curve connecting (0,2) to (1,1) to (2,1) to (3,2) to (5,1).$
Evaluate $B(x)$ for $x = 1$, $2$, $3$, $4$ and $5$.
Let $C(x)$ represent the area bounded by the graph of the function shown below, the horizontal axis, and vertical lines at $t=0$ and $t=x$:
$A red line segment in the first quadrant labeled y=1+t and passing through (0,1) and (3,4).$
Evaluate $C(x)$ for $x = 1$, $2$ and $3$, and use that information to deduce a formula for $C(x)$.
Let $A(x)$ represent the area bounded by the graph of the function shown below, the horizontal axis, and vertical lines at $t=0$ and $t=x$: FIGURE Evaluate $A(x)$ for $x = 1$, $2$ and $3$, and find a formula for $A(x)$.
The figure below shows the velocity of a car during a 30-second time frame:
$A red line segment in the first quadrant labeled y=4-t and passing through (0,4) and (4,0).$
How far did the car travel between $t=0$ to $t=30$ seconds?
The figure below shows the velocity of a car during a 30-second time frame:
$A black piecewise-linear curve connecting (0,30) to (20,30) to (30,0). The region below the curve and above the horizontal axis is shaded pink. The vertical axis is labeled 'velocity (feet/sec).$
How far did the car travel between $t=0$ to $t=30$ seconds?
The figure below shows the velocities of two cars:

From the time the brakes were applied:
1. how long did it take each car to stop?
2. which car traveled farther before stopping?
A speeder traveling 45 miles per hour (in a 25-mph zone) passes a stopped police car, which immediately takes off after the speeder. If the police car speeds up steadily to 60 mph over a 10-second interval and then travels at a constant 60 mph, how long — and how far — will it be before the police car catches the speeder, who continued traveling at 45 mph?
$A red piecewise-linear curve labeled 'A' connects (0,80) to (20,80) to (40,0). A blue piecewise-linear curve labeled 'B' connects (0,40) to (20,40) to (60,0). The horizontal axis is labeled 'time (seconds)' and the vertical axis 'velocity (feet/sec).'$