4.A: Answers

Last updated
Save as PDF

Page ID: 212041

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\dsum}{\displaystyle\sum\limits} $

$ \newcommand{\dint}{\displaystyle\int\limits} $

$ \newcommand{\dlim}{\displaystyle\lim\limits} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$\newcommand{\longvect}{\overrightarrow}$

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Section 4.0

1. $(10)(12) + (8)(4) = 152$
2. $(10)(20) - (3)(8) = 176$
$bh + \frac12 b(H - h) = bh + \frac12 bH - \frac12 bh = b\left(\frac{h + H}{2}\right)$
1. $1\cdot 3 + 1\cdot 2 = 5$
2. area $< 5$
Answers will vary from $5$ to $13$.
$A(1) = 1$, $A(2) = 2.5$, $A(3) = 4.5$, $A(4) = 6$, $A(5) = 7$
$C(1) = 1.5$, $C(2) = 4$, $C(3) = 7.5$, $C(x)$ is sum of rectangular and triangular areas:\[C(x) = x + \frac12 x\cdot x = x + \frac12 x^2\nonumber\]
$(20)(30) + \frac12 (10)(30) = 600 + 150 = 750$ feet
1. $A$: 20 seconds to stop; $B$: 40 seconds to stop
2. $A$: $\frac12 (20)(80) = 800$ ft; $B$: $\frac12 (40)(40) = 800$ ft
miles, $, ft$^3$, kilowatt-hours, people, square meals

Section 4.1

$2^2 + 3^2 + 4^2 = 29$
$(1+1)^2 + (1+2)^2 + (1+3)^2 = 29$
$\cos(0) + \cos(\pi) + \cos(2\pi) + \cos(3\pi) + \cos(4\pi) + \cos(5\pi) = 1 + (-1) + 1 + (-1) + 1 + (-1) = 0$
$\displaystyle \sum_{k=3}^{94} k$
$\displaystyle \sum_{k=3}^{12} k^2$
$\displaystyle \sum_{k=1}^{7} k\cdot 2^k$
1. $(1+2) + (2+2) + (3+2) = 3 + 4 + 5 = 12$
2. $(1+2+3) + (2+2+2) = 12$
1. $5\cdot 1 + 5\cdot 2 + 5\cdot 3 = 5 + 10 + 15 = 30$
2. $5\cdot (1 + 2 + 3) = 5\cdot 6 = 30$
1. $1^2 + 2^2 + 3^2 = 1 + 4 + 9 = 14$
2. $(1 + 2 + 3)^2 = 6^2 = 36$
$f(0) + f(1) + f(2) + f(3) = 0^2 + 1^2 + 2^2 + 3^2 = 14$
$2\cdot f(0) + 2\cdot f(1) + 2\cdot f(2) + 2\cdot f(3) = 2\cdot 0 + 2\cdot 1 + 2\cdot 4 + 2\cdot 9 = 28$
$g(1) + g(2) + g(3) = 3 + 6 + 9 = 18$
$g^2(1) + g^2(2) + g^2(3) = 3^2 + 6^2 + 9^2 = 126$
$h(2) + h(3) + h(4) = \frac22 + \frac23 + \frac24 = \frac{13}{6}$
$f(1)h(1) + f(2)h(2) + f(3)h(3) =(1)(2) + (4)(1) + (9)\left(\frac23\right) = 12$
$\left(1^2 - 0^2\right) + \left(2^2 - 1^2\right) + \left(3^2 - 2^2\right) + \left(4^2 - 3^2\right) + \cdots + \left(7^2 - 6^2\right) = 7^2 - 0^2 = 49$
$\left(\frac11-\frac12\right) + \left(\frac12-\frac13\right) + \left(\frac13-\frac14\right) + \left(\frac14-\frac15\right) + \left(\frac15-\frac16\right) = 1-\frac16 = \frac56$
$\left(\sqrt{1} - \sqrt{0}\right) + \left(\sqrt{2} - \sqrt{1}\right) + \left(\sqrt{3} - \sqrt{2}\right) + \left(\sqrt{4} - \sqrt{3}\right) + \cdots + \left(\sqrt{9} - \sqrt{8}\right) = 3-0 = 3$
1. $[2, 3]$, $[3, 4.5]$, $[4.5, 6]$, $[6, 7]$
2. $1$, $1.5$, $1.5$, $1$
3. mesh $= 1.5$
4. $1 + 1.5 + 1.5 + 1 = 5$
1. $[-3, -1]$, $[-1, 0]$, $[0, 1.5]$, $[1.5, 2]$
2. $2$, $1$, $1.5$, $0.5$
3. mesh $= 2$
4. $2 + 1 + 1.5 + 0.5 = 5$
1. $[3, 3.8]$, $[3.8, 4.5]$, $[4.5, 5.2]$, $[5.2, 7]$
2. $0.8$, $0.7$, $0.7$, $1.8$
3. mesh $= 1.8$
4. $0.8+0.7+ 0.7+ 1.8 = 4$
$\Delta x_1 + \Delta x_2 + \cdots + \Delta x_n = (x_1 - x_0) + (x_2 - x_1) + (x_3 - x_2) + \cdots + (x_n - x_{n-1}) = x_n - x_0$
1. $A graph of a blue, concave-down, descending curve in the first quadrant from (0,4) to (2,0). Horizontal black line segments extend from (0,4) to (1,4), (1,3) to (1.5,3) and (1.5,0) to (2,0). Dashed-black vertical line segments extend from (1,0) to (1,4) and from (1.5,0) to (1.5,3). The rectangular regions below the solid horizontal line segments, vertical dashed line segments and the coordinate axes are shaded yellow.$
  $f(0)(1) + f(1)(0.5) + f(2)(0.5) = (4)(1) + (3)(0.5) + (0)(0.5) = 5.5$
2. $f(1)(1) + f(1.5)(0.5) + f(1.5)(0.5) = (3)(1) + (1.75)(0.5) + (1.75)(0.5) = 4.75$
1. $A graph of a blue, concave-down curve in the first quadrant rising from (0,0) to a peak at (pi/2,1), then falling to (pi,0). Horizontal dashed-black line segments extend from (pi/4,0.71) to (pi/2,0.71) and from (pi/2,1) to (pi,1). Dashed-black vertical line segments extend from the ends of the horizontal line segments down to the x-axis. The rectangular regions abounded by the dashed segments and the x-axis are shaded yellow.$
  $\left(\frac{\pi}{4}\right)(0) + \left(\frac{\pi}{4}\right)(\frac{1}{\sqrt{2}}) + \left(\frac{\pi}{2}\right)(1) \approx 2.13$
2. $\left(\frac{\pi}{4}\right)(\frac{1}{\sqrt{2}}) + \left(\frac{\pi}{4}\right)(1)+\left(\frac{\pi}{2}\right)(0) \approx 1.34$
1. $(2)(1) + (5)(2) + (17)(1) \leq \mbox{RS} \leq (5)(1) + (17)(2) + (26)(1) \ \Rightarrow \ 29 \leq \mbox{RS} \leq 65$
2. $(2)(1) + (5)(1) + (10)(1) + (17)(1) \leq \mbox{RS} \leq (5)(1) + (10)(1) + (17)(1) + (26)(1)\ \Rightarrow \ 34 \leq \mbox{RS} \leq 58$
3. $2(0.5) + 3.25(0.5) + 5(1) + 10(1) + 17(1) \leq \mbox{RS} \leq 3.25(0.5) + 5(0.5) + 10(1) + 17(1) + 26(1) \Rightarrow 34.625 \leq \mbox{RS} \leq 57.125$
1. $(0)\left(\frac{\pi}{2}\right) + (0)\left(\frac{\pi}{2}\right) \leq \mbox{RS} \leq (1)\left(\frac{\pi}{2}\right) + (1)\left(\frac{\pi}{2}\right) \ \Rightarrow \ 0 \leq \mbox{RS} \leq \pi$
2. $0\left(\frac{\pi}{4}\right) + \frac{1}{\sqrt{2}}\left(\frac{\pi}{4}\right) + 0\left(\frac{\pi}{2}\right) \leq \mbox{RS} \leq \frac{1}{\sqrt{2}}\left(\frac{\pi}{4}\right) + 1\left(\frac{\pi}{4}\right) + 1\left(\frac{\pi}{2}\right) \Rightarrow \ 0.56 \leq \mbox{RS} \leq 2.91$
3. $0\left(\frac{\pi}{4}\right) + \frac{1}{\sqrt{2}}\left(\frac{\pi}{4}\right) + \frac{1}{\sqrt{2}}\left(\frac{\pi}{4}\right) + 0\left(\frac{\pi}{4}\right) \leq \mbox{RS} \leq \frac{1}{\sqrt{2}}\left(\frac{\pi}{2}\right) + 1\left(\frac{\pi}{4}\right) + 1\left(\frac{\pi}{4}\right)+ \frac{1}{\sqrt{2}}\left(\frac{\pi}{4}\right) \Rightarrow \ 1.11 \leq \mbox{RS} \leq 2.68$
1. $\left| 7.402 - 7.362 \right| = 0.04$
2. $\left| 7.390 - 7.372 \right| = 0.018$
$\left|\mbox{error}\right| = (\mbox{base})(\mbox{height}) = \frac{4 - 2}{50}\left(65 - 9\right) = \frac{56}{25} = 2.24$

$\frac{100(101)}{2} = 5050$

$S =$	$1$	$+$	$2$	$+$	$3$	$+$	$\cdots$	$+$	$100$
$+\ S =$	$100$	$+$	$99$	$+$	$98$	$+$	$\cdots$	$+$	$1$
$2S =$	$101$	$+$	$101$	$+$	$101$	$+$	$\cdots$	$+$	$101$

so $2S = \ 100(101) \ = \ 10100 \ \Rightarrow \ S = 5050$

$10 + 11 + 12 + \cdots + 20 = (1+2+3 + \cdots + 20) - (1+2+3 + \cdots + 9) = \frac{20(21)}{2} - \frac{9(10)}{2} = 210 - 45 = 165$
$\displaystyle \sum_{k=1}{10}\, (k^3 + k) = \sum_{k=1}{10}\, k^3 + \sum_{k=1}{10}\, k = \left[\frac{10(11)}{2}\right]^2 + \left[\frac{10(11)}{2}\right] = (55)^2 + 55 = 3080$

Section 4.2

$\displaystyle \int_0^4 \left[2+3x\right]\, dx$
$\displaystyle \int_2^5 \cos(5x) \, dx$
$\displaystyle \int_1^5 x^3 \, dx$
$\displaystyle \int_{0.5}^2 x\cdot \sin(x)\, dx$
$\displaystyle \int_1^3 \ln(x) \, dx$
$\displaystyle \int_1^3 2x \, dx = 8$
$\displaystyle \int_{-1}^0 \left|x\right| \, dx = \frac12$
$\displaystyle \int_0^4 \left[3-\frac{x}{2}\right]\, dx = 8$
1. $3$
2. $-1$
3. $6$
4. $8$
5. $7$
1. $A graph of a blue curve on a [0,10]X[-10,20] grid, with the horizontal axis labeled 'minutes' and the vertical axis labeled 'feet.' The curve begins as a straight line between the origin and (5,10) then bends upward in a U shape to (6,16), then transitions to an inverted-U shape, reaching a peak near (8,19).$
2. 24 ft
3. 24 feet from starting point
meters
ft$^3$
gram-meters
ft/sec
$\Delta x = \frac{2-0}{n} = \frac{2}{n}$, $m_k = \frac{2}{n}(k - 1)$, $M_k = \frac{2}{n}k$, so $f(m_k) = \left[\frac{2}{n}(k-1)\right]^3$ and $f(M_k) = \left[\frac{2}{n}k\right]^3$
1. $\displaystyle \mbox{LS} = \sum_{k=1}^n f(m_k)\, \Delta x = \sum_{k=1}^n \, \left[\frac{2}{n}(k-1)\right]^3 \Delta x =\frac{2}{n}\cdot\frac{8}{n^3}\left[\sum_{k=1}^n \, k^3 - 3 \sum_{k=1}^n \, k^2 + 3 \sum_{k=1}^n \, k - \sum_{k=1}^n \, 1\right]$
  $\displaystyle = \frac{16}{n^4} \left[\left(\frac14 n^4 + \frac12 n^3 + \frac{3}{12} n^2\right)-3\left(\frac13 n^3 + \frac12 n^2 + \frac{2}{12} n\right) + 3\left( \frac12 n^2 + \frac12 n\right)-n\right]$
  $\displaystyle = \frac{16}{n^4}\left[\frac14 n^4 - \frac12 n^3 +\frac14 n^2\right] = 4 - \frac{8}{n} + \frac{4}{n^2} \longrightarrow 4$
2. $\displaystyle \mbox{US} = \sum_{k=1}^n f(M_k)\, \Delta x = \sum_{k=1}^n \, \left[\frac{2}{n}(k)\right]^3 \frac{2}{n} = \frac{16}{n^4}\left[\sum_{k=1}^n \, k^3\right] = \frac{16}{n^4}\left[\frac14 n^4 + \frac12 n^3 +\frac{3}{12} n^2\right] = 4 + \frac{8}{n} + \frac{4}{n^2} \longrightarrow 4$

Section 4.3

$5$
$0$
$3$
$0$
$-5$
$-5$
$0$
$4.5+5 = 9.5$
$10+3 = 13$
$5+2 = 7$
$1$
$-1$
$2$
$1$
$1$
1. $8\cdot 6 = 48$
2. $24$
1. $32$
2. $8^2 = 64$
$8$
$2.5$
$3$
$7$
1. $y = A(x) = \frac12 x^2$ (below left)
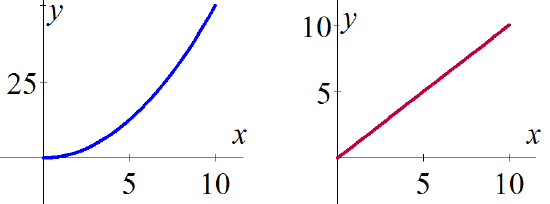
  $Two graphs in the first quadrant: a blue graph of y=0.5x^2 is on the left and a red graph of y=x is on the right.$
2. $y = A'(x) = x$ (above right)
1. $A blue curve in the first quadrant, that starts increasing slowly in a U shape from where the input is 0, transitions to an inverted-U shape near where the input is 2, reaches a peak near 3, descends a bit and transitions to a U shape, then reaches a low point at 4 before curving upward again.$
2. $A red pieceswise-linear curve that ascends through the origin to a peak between inputs of 2 and 3, then descends through (3,0) to a low point near where the input is 3.4, then bends upward, passing through (4,0).$
1. $f$ is continuous on $[1, 4]$
2. $f$ is not differentiable on $[1,4]$ (not differentiable at $x \approx 2.5$ and $x \approx 3.3$)
3. $f$ is integrable on $[1,4]$
1. $f$ is not continuous on $[1, 4]$ (not continuous at $x=2$)
2. $f$ is not differentiable on $[1,4]$ (not differentiable at $x=2$)
3. $f$ is integrable on $[1,4]$
$\int_1^4 v(t)\, dt = \int_1^2 v(t)\, dt + \int_2^4 v(t)\, dt = 35 + 50 = 85$ miles
1. The rectangle associated with the interval containing $x=2$ has width $w$ and height $5$, so its area is $5w$; all of the other rectangles have the same height ($7$) and the sum of their widths is $(4-1)-w = 3-w$, so their total area is $7(3-w)$: $\mbox{RS} = 5w + 7(3-w)$
2. Because $0 < w \leq \left\|{\cal P}\right\|$, as $\left\|{\cal P}\right\| \rightarrow 0 \Rightarrow w \rightarrow 0$ so $\displaystyle \lim_{\left\|{\cal P}\right\| \to 0} \, \mbox{RS} = \lim_{w \to 0} \, \left[5w + 7(3-w)\right] = 21$
3. $\int_1^4 g(x)\, dx =$ $\displaystyle \lim_{\left\|{\cal P}\right\| \to 0} \mbox{RS} = 21$
  $\int_1^4 7 \, dx = 7(4-1) = 7(3) = 21$
4. A (very) similar argument shows that redefining any constant function $f$ at a single point does not alter the value of $\int_a^b f(x)\, dx$. A (somewhat) similar argument can extend this result to all integrable functions.

Section 4.4

1. See figure below left.
2. $A(1) = 0$, $A(2) = 1.5$, $A(3) = 4$, $A(4) = 6.5$
3. $A'(1) = 1$, $A'(2) = 2$, $A'(3) = 3$, $A'(4) = 2$
$Two blue graphs with tickmarks on the x-axis at 1, 2, 3, 4 and 5. The left graph has tickmarks on the vertical axis at 4 and 8, with curve starting at (1,0) and increasing in a U shape through (2,1.5) to (3,4), where it adopts an inverted-U shape and passes through (4,6.5) and (5,8) before beginning to flatten out; dashed-black vertical and horizontal line segments extend from the axes to the points on the graph with integer inputs. The right graph has tickmarks on the vertical axis at -2, -1 and 1, with the curve starting in an inverted-U shape at (1,0), reaching a peak near (2,0.4), then curving down to (3,0), where it becomes roughly linear (with a negative slope).$
1. See figure above right.
2. $A(1) = 0$, $A(2) = 0.5$, $A(3) = 0$, $A(4) = -1$
3. $A'(1) = 1$, $A'(2) = 0$, $A'(3) = -1$, $A'(4) = -1$
1. See figure below left.
2. $A(1) = 0$, $A(2) = 2$, $A(3) = 4$, $A(4) = 6$
3. $A'(1) = 2$, $A'(2) = 2$, $A'(3) = 2$, $A'(4) = 2$
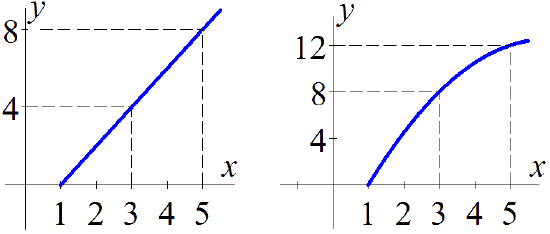
$Two blue graphs with tickmarks on the x-axis at 1, 2, 3, 4 and 5. The left graph has tickmarks on the vertical axis at 4 and 8, with linear curve starting at (1,0) and passing through (3,4) and (5,8); dashed-black vertical and horizontal line segments extend from the axes to the points (3,4) and (5,8). The right graph has tickmarks on the verical axis at 4, 8 and 12, with the curve starting in an inverted-U shape at (1,0), passing through (3,8) and (5,12) before beginning to flatten out; dashed-black vertical and horizontal line segments extend from the axes to the points (3,8) and (5,12).$
1. See figure above right.
2. $A(1) = 0$, $A(2) = 4.5$, $A(3) = 8$, $A(4) = 10.5$
3. $A'(1) = 5$, $A'(2) = 4$, $A'(3) = 3$, $A'(4) = 2$
1. $\displaystyle x^2\Big|_0^3 = 9$
2. $\displaystyle x^2\Big|_1^3 = 8$
3. $\displaystyle x^2\Big|_0^1 = 1$
1. $\displaystyle 2x^3\Big|_1^3 = 52$
2. $\displaystyle 2x^3\Big|_1^2 = 14$
3. $\displaystyle 2x^3\Big|_0^3 = 54$
1. $\displaystyle x^4\Big|_0^3 = 81$
2. $\displaystyle x^4\Big|_1^3 = 80$
3. $\displaystyle x^4\Big|_0^1 = 1$
1. $\displaystyle x^3\Big|_{-3}^3 = 54$
2. $\displaystyle x^3\Big|_{-3}^0 = 27$
3. $\displaystyle x^3\Big|_0^3 = 27$
1. $\displaystyle x^3\Big|_0^2 = 8$
2. $\displaystyle x^3\Big|_1^3 = 26$
3. $\displaystyle x^3\Big|_3^1 = -26$
1. $\displaystyle \int_0^{10} 2t\, dt = t^2\Big|_0^{10} = 100$ ft
2. $\displaystyle 50 = \int_0^{T} 2t\, dt = T^2 \Rightarrow T = \sqrt{50} \approx 7.07$ sec
1. $\displaystyle \int_0^{10} 4t^3\, dt = t^4\Big|_0^{10} = 10000$ ft
2. $\displaystyle 5000 = \int_0^{T} 4t^3\, dt = T^4 \Rightarrow T = %\sqrt[4]{5000} \approx 8.41$ sec
1. $75-3t^2=0 \Rightarrow t = 5$ sec
2. $\displaystyle \int_0^{5} \left[75-3t^2\right]\, dt = 75t-t^3\Big|_0^{5} = 250$ ft
3. $\displaystyle 125 = \int_0^{T} \left[75-3t^2\right]\, dt = 75T-T^3$, so use a graph of $y = x^3-75x+125$ (or Newton’s method) to solve for $T \approx 1.74$ sec
The total area is $\displaystyle \int_0^3 x^2\, dx = \frac13 x^3\Big|_0^3 = \frac13\cdot 27 = 9$.
1. $\displaystyle \frac12\cdot 9 = \frac13 x^3\Big|_0^T = \frac13 T^3 \Rightarrow T = \sqrt[3]{\frac{27}{2}} \approx 2.38$
2. $\displaystyle \frac13\cdot 9 = \int_0^T x^2\, dx = \frac13 T^3 \Rightarrow T = \sqrt[3]{9} \approx 2.08$
  $\displaystyle \frac23\cdot 9 = \int_0^T x^2\, dx = \frac13 T^3 \Rightarrow T = \sqrt[3]{18} \approx 2.62$

Section 4.5

1. $A(x) = x^3 \Rightarrow A'(x) = 3x^2$ so $A'(1) = 3$, $A'(2) = 12$ and $A'(3) = 27$
2. $A'(x) = \mbox{D}\left[\int_0^x 3t^2\, dt \right] = 3x^2$ so $A'(1) = 3$, $A'(2) = 12$ and $A'(3) = 27$
$A'(x) = 2x$ so $A'(1) = 2$, $A'(2) = 4$, $A'(3) = 6$
$A'(x) = 2x$ so $A'(1) = 2$, $A'(2) = 4$, $A'(3) = 6$
$A'(1) \approx 0.84$, $A'(2) \approx 0.91$, $A'(3) \approx 0.14$
$A'(x) = f(x)$, $A'(1) = 2$, $A'(2) = 1$, $A'(3) = 2$
$A'(x) = f(x)$, $A'(1) = 1$, $A'(2) = 2$, $A'(3) = 2$
$F(1) - F(0) = 6 - 5 = 1$
$F(3) - F(1) = 9 - \frac13 = \frac{26}{3}$
$F(5) - F(1) \approx 1.61 - 0 = 1.61$
$F(3) - F\left(\frac12\right) \approx 1.10 - (-0.69) = 1.79$
$F\left(\frac{\pi}{2}\right) - F(0) = 1 - 0 = 1$
$F(1) - F(0) \approx 0.67 - 0 = 0.67$
$F(7) - F(1) = \frac23(7)^{\frac32} - \frac23 \approx 11.68$
$F(9) - F(1) = 3 - 1 = 2$
$F(3) - F(-2) \approx 20.09 - 0.14 = 19.95$
$F\left(\frac{\pi}{4}\right) - F(0) = 1 - 0 = 1$
$F(3) - F(0) = \frac23 (10)^{\frac32} - \frac23 \approx 20.42$
$F(x) = \frac13 x^3 \Rightarrow F(2) - F(-1) = \frac83 - \left( -\frac13\right) = 3$
$F(x) = \ln(x) \Rightarrow F(e) - F(1) = 1 - 0 = 1$
$F(x) = \frac23 x^{\frac32} \Rightarrow F(100) - F(25) = \frac{2000}{3} - \frac{250}{3} = \frac{1750}{3}$
$F(x) = -\frac{1}{x} \Rightarrow F(10) - F(1) = - 0.1 - (-1) = 0.9$
$F(x) = e^x \Rightarrow F(1) - F(0) = e - 1 \approx 1.718$
$F(x) = \tan(x) \Rightarrow F\left(\frac{\pi}{4}\right) - F\left(\frac{\pi}{6}\right) = 1 - \frac{1}{\sqrt{3}} \approx 0.423$
$\int_3^3 f(x)\, dx = 0$ for any integrable $f$
$\displaystyle \int_0^{\pi} \sin(x)\, dx = -\cos(x)\Big|_0^{\pi} = -(-1) - (-1) = 2$
$\displaystyle \int_0^{3.5} \lfloor x \rfloor \, dx = 0 + 1 + 2 + \frac12 (3) = 4.5$
$\displaystyle \int_0^3 (x-2)^2 \, dx = \int_0^3 (x^2-4x+4) \, dx = \frac13 x^3 - 2x^2 + 4x\Big|_0^3 =3$
$\mbox{D}\left(A(3x)\right) = 3\tan(3x)$, $\mbox{D}\left(A(x^2)\right) = 2x\tan(x^2)$, $\mbox{D}\left(A(\sin(x)\right) = \cos(x)\tan(\sin(x))$
$\sqrt{1 + 5x}(5)$
$\sqrt{1 + \sin(x)} \cdot \cos(x)$
$\left[3(1-2x)^2 + 2\right](-2)$
$-\cos(3x)$
$\tan(x^2)\cdot 2x - \tan(x)$
$5\ln(x)\cos(3\ln(x))\cdot\frac{1}{x}$

Section 4.6

$\displaystyle \frac14 x^4\Big|_1^2 = \frac{15}{4} \neq \frac72 = \left[\frac13 x^3\Big|_1^2\right]\left[\frac12 x^2\Big|_1^2\right]$
$\displaystyle \frac14 \neq \frac13 \cdot \frac12$
$\displaystyle \frac13\sin(3x) + C$
$-\cos(2 + e^x) + C$
$\tan(\sin(x)) + C$
$\displaystyle \frac52\ln\left| 3 + 2x \right| + C$
$\displaystyle -\frac13 \cos(1 + x^3) + C$
$\displaystyle \frac14\sin(4x) + C$
$\frac{1}{48}\left(5 + x^4\right)^{12} + C$
$\ln\left| 2 + x^3\right| + C$
$\displaystyle \frac12\left(\ln(x)\right)^2 + C$
$\frac{1}{24}\left( 1 + 3x \right)^8 + C$
$\sec\left(e^x\right) + C$
$\displaystyle \frac13 \sin(3x) \Big|_0^{\frac{\pi}{2}} = -\frac13$
$\displaystyle -\cos\left(2 + e^x\right)\Big|_0^1 \approx -0.996$
$\displaystyle \frac{1}{18}\left(1 + x^3\right)^6\Big|_{-1}^1 = \frac{32}{9}$
$\displaystyle \frac{5}{2}\ln\left|3 + 2x\right|\Big|_{0}^2 = \frac52\ln\left(\frac73\right)$
$\displaystyle -\frac{1}{3}\left(1 - x^2\right)^{\frac32}\Big|_{0}^1 = \frac13$
$\displaystyle \frac{2}{9}\left(1 +3x\right)^{\frac32}\Big|_{0}^1 = \frac{14}{9}$
$\frac{1}{2}x - \frac{1}{20}\sin(10x)+ C$
$\frac{1}{4}\sin(2x)+ C$
$\frac{1}{2}x - \frac{1}{4}\sin(2x)\Big|_{0}^{\pi} = \frac{\pi}{2}$
$\frac17 x^7 + \frac35 x^5 + x^3 + x + C$}
$\frac12 e^{2x} + 2e^x + x + C$
$\frac16 x^6 + \frac14 x^4 + \frac53 x^3 + 5x + C$
$\frac12 e^{2x} + \frac14 e^{4x} + C$
$\frac27 x^{\frac72} + \frac65 x^{\frac52} - \frac43 x^{\frac32} + C$
$3x - 3\ln\left| x + 1 \right| + C$
$\frac12 x^2 - x + C$
$x^2 - 11x + 7\ln\left| x - 1 \right| + C$
$x+3\ln\left| x - 1 \right| + C$
$\frac23 x^{\frac32} + 8 x^{\frac12} + C$
$\mbox{area of semicircle with radius 1} = \frac12 \pi(1)^2 = \frac{\pi}{2}$
$\mbox{area of semicircle with radius 3} = \frac12 \pi(3)^2 = \frac{9\pi}{2}$
$(2)(2)+\frac12 \pi(1)^2 = 4+\frac{\pi}{2}$

Section 4.7

Answers will vary between $11$ (using left endpoints) and $6$ (using right endpoints).
Between $4$ (left endpoints) and $6$ (right).
Using left-hand widths:\[(40)\left[0+70+55+90+130+115\right] = 18400 \mbox{ ft}^2\nonumber\]Right-hand widths ($70$, $55$, … ) and average widths ($\frac{70}{2}$, $\frac{125}{2}$, … ) yield the same result.
$\displaystyle \int_{-1}^{2} \left[(x^2+3)-1\right]\, dx = 9$
$\displaystyle \int_{0}^{1} \left[x-x^2\right]\, dx + \int_{1}^{2} \left[x^2-x\right]\, dx= 1$
$\displaystyle \int_{1}^{e} \left[x-\frac{1}{x}\right]\, dx = \frac12 e^2 - \frac32$
$\displaystyle \int_{0}^{\frac{\pi}{4}} \left[(x+1)-\cos(x)\right]\, dx = \frac{1}{32}{\pi}^2 + \frac14 \pi - \frac{\sqrt{2}}{2}$
$\displaystyle \int_{0}^{2} \left[e^x-x\right]\, dx = e^2 - 3$
$\displaystyle \int_{0}^{1} \left[3-\sqrt{1-x^2}\right]\, dx = 3 - \frac{\pi}{4}$
Using ${\cal P} = \left\{0.5, 1.5, 2.5, 3.5, 4.5\right\}$, so that $\Delta x = 1$, and $c_1 = 1$, $c_2 = 2$, $c_3 = 3$, $c_4 = 4$:\[\frac{1}{4.5-0.5} \int_{0.5}^{4.5} f(x)\, dx \approx \frac14\left[6+6+4+3\right](1) = \frac{19}{4}\nonumber\]
With ${\cal P} = \left\{1.5, 2.5, 3.5\right\}$, $\Delta x = 1$, $c_1 = 2$, $c_2 = 3$:\[\frac{1}{3.5-1.5} \int_{0.5}^{3.5} f(x)\, dx \approx \frac12\left[6+4\right](1) = \frac{10}{2}=5\nonumber\]
$\displaystyle \frac{1}{2-0}\int_{0}^{2} f(x)\, dx = \frac22 = 1$
$\displaystyle \frac{1}{6-1}\int_{1}^{6} f(x)\, dx = \frac{11}{5}$
$\displaystyle \frac{1}{4-0}\int_{0}^{4} \left[2x+1\right]\, dx = 5$
$\displaystyle \frac{1}{3-1}\int_{1}^{3} x^2\, dx = \frac{13}{3}$
$\displaystyle \frac{1}{\pi -0}\int_{0}^{\pi} \sin(x)\, dx = \frac{2}{\pi}$
$C = 1$: $\overline{f} = \frac23$; $C = 9$: $\overline{f} = 2$; $C = 81$: $\overline{f} = 6$; $C = 100$: $\overline{f} = \frac{20}{3}$. In general, $\overline{f} = \frac23 \sqrt{C}$.
1. About 180 miles
2. About 36 mph
1. 1,950 foot-pounds
2. 1,312.5 foot-pounds
1. 1,200 ft-lbs
2. 600 ft-lbs
3. 400 foot-lbs
1,275 foot-pounds

Section 4.8

$\displaystyle \frac12 \arctan\left(\frac{x}{2}\right) + C$
$\displaystyle x^2 + \frac25 \arctan\left(\frac{x}{5}\right) + C$
$\displaystyle \frac13 \ln\left|\frac{x+3}{x-3}\right| + C$
$\displaystyle \frac{1}{\sqrt{3}} \arctan\left(\frac{x}{\sqrt{3}}\right) + C$
$\displaystyle e^x + \frac{7}{\sqrt{2}} \arctan\left(\frac{x}{\sqrt{2}}\right) + C$
$\displaystyle 3\arcsin\left(\frac{x}{\sqrt{5}}\right) + C$
$\displaystyle \frac{1}{10} \arctan\left(\frac{5x}{2}\right) + C$
$\displaystyle \frac52 \arcsin\left(2x\right) + C$
$\displaystyle \frac23\ln\left|3x+\sqrt{1+9x^2}\right| + C$
$\displaystyle (x+1)\ln\left(x+1\right) - x+K$
$\displaystyle \frac{3}{10}(5x^2+7)\left[\ln\left(5x^2+7\right) -1\right]+C$
$\displaystyle \sin(x)\left[\ln\left| \sin(x)\right| - 1\right]+C$
$\displaystyle \frac{x}{2}\sqrt{x^2+4}+2\ln\left|x+\sqrt{x^2+4}\right|+C$
$\displaystyle \frac{x}{2}\sqrt{x^2+16}+8\ln\left|x+\sqrt{x^2+16}\right|+C$
$\displaystyle 8 + \frac25\left[\arctan\left(\frac35\right)-\arctan\left(\frac15\right)\right]$
$\displaystyle \frac{1}{\sqrt{3}}\arctan\left(\frac{x}{\sqrt{3}}\right)\Big|_{-1}^1 = \frac{\pi}{3\sqrt{3}}$
$\displaystyle 3\left[\arcsin\left(\frac{2}{\sqrt{5}}\right)-\arcsin\left(\frac{1}{\sqrt{5}}\right)\right]$
$\displaystyle \frac52 \arcsin\left(2x\right)\Big|_{0}^{0.1} = \frac52\arcsin(0.2)$
$7\ln(7) - 6$
$3\ln(3) - 2\ln(2) - 1$
$\displaystyle 3\sqrt{18} + \frac92\ln\left(\frac{3 + \sqrt{18}}{-3 + \sqrt{18}}\right)$
$\displaystyle -\frac13 \sin^2(x)\cos(x) -\frac23 \cos(x) + C$
$\displaystyle \frac15 \cos^4(x)\sin(x) + \frac45 \int \cos^3(x)\, dx$
$x^2\sin(x) + 2x\cos(x) - 2\sin(x) + C$
average of $\sin(x) = \frac{2}{\pi} > \frac12 =$ average of $\sin^2(x)$
$C=e$: $\frac{1}{e-1}$; $C=10$: $\frac19 \left[10\ln(10)-9\right]$; $C= 100$: $\frac{1}{99} \left[100\ln(100)-99\right]$; $C= 1000$: $\frac{1}{999} \left[1000\ln(1000)-999\right]$
1. $e^2-e \approx 4.67$
2. $e^2 \approx 7.39$
3. $2e^2-e \approx 12.06$
$2\arctan(C) \approx 1.57$, $2.94$, $3.04$, $3.07$, $3.09$

Section 4.9

$T_4 = \frac12\left[2.1 + 2(3.8) + 2(0.3) + 2(-0.9) + 2.2\right] = 5.35$
$S_4 = \frac13 \left[2.1 + 4(3.8) + 2(0.3) + 4(-0.9) + 2.2\right] = 5.5$}
$T_8 = 7.35$, $\displaystyle S_8 = \frac{22}{3} \approx 7.3333$
1. $T_4 = 4$
2. $S_4 = 4$
3. $4$
1. $T_4 = 0.75$
2. $S_4 = \frac23 \approx 0.67$
3. $\displaystyle \frac23$
1. $T_4 = 1.896118898$
2. $S_4 = 2.004559755$
3. $2$
1. $T_6 = 1.088534906$
2. $S_6 = 1.090560447$
1. $T_6 = 3.815780054$
2. $S_6 = 3.826350295$
1. $T_6 = 0.8159928163$
2. $S_6 = 0.8120491229$
1. $f(x) = x \Rightarrow f''(x) = 0 \Rightarrow B_2 = 0$, so the error bound is $0$ (the Trapezoidal approximation is exact)
2. $f^{(4)}(x) = 0 \Rightarrow B_4 = 0$, so the error bound is $0$ (the Simpson’s Rule approximation is exact)
3. $n = 1$
4. $n = 2$ (must be an even integer)
1. $f(x) = x^3 \Rightarrow f''(x) = 6x$ so when $\left|x\right|\leq 1$, $\left|f''(x)\right| \leq 6$; taking $B_2 = 6$, $\left|\mbox{error}\right| \leq \frac{2^3\cdot 6}{12\cdot 4^2} = 0.25$
2. $f^{(4)}(x) = 0 \Rightarrow B_4 = 0$, so error bound is $0$
3. $\frac{2^3\cdot 6}{12\cdot n^2} \leq 0.001 \Rightarrow n^2 \geq 4000 \Rightarrow n \geq 63.25$, so take $n = 64$
4. $n=2$
1. $f''(x) = -\sin(x) \Rightarrow \left|f''(x)\right| \leq 1 \Rightarrow B_2 = 1$, so $\left|\mbox{error}\right| \leq \frac{\pi^3\cdot 1}{12\cdot 4^2} \approx 0.1612$
2. $f^{(4)}(x) = \sin(x) \Rightarrow$ $\left|f^{(4)}(x)\right| \leq 1 = B_4$, so $\left|\mbox{error}\right| \leq \frac{\pi^5\cdot 1}{180\cdot 4^4} \approx 0.0066$
3. $\frac{\pi^3\cdot 1}{12\cdot n^2} \leq 0.001$ $\Rightarrow n^2 \geq \frac{1000\pi^3}{12} \Rightarrow n \geq 50.83$, so take $n = 51$
4. $\frac{\pi^5\cdot 1}{180\cdot n^4} \leq 0.001 \Rightarrow n^4 \geq \frac{1000\pi^3}{180} \Rightarrow$ $n \geq 6.42$, so take $n = 8$
$S_6 = \frac{30}{3}[50 + 4(62) + 2(92) + 4(86) + 2(74)$; $+ 4(50) + 40] = 12140$ ft\)^2\)
area: $S_6 \approx 37166.7$ ft$^2$; volume: $(37166.7)(22) =$ 817,667 ft$^3$
distance $\approx T_{10} =$ 4,010 ft
On your own.
On your own.
1. $L_4 = 3.5$
2. $R_4 = 4.5$
3. $M_4 = 4$
4. $4$
1. $L_4 = 0.75$
2. $R_4 = 0.75$
3. $M_4 = 0.625$
4. $\frac23$\
1. $1.8961$
2. $1.8961$
3. $2.0523$
4. $2$
On your own.
$S_{10} = 6.12572$; $S_{40} = 6.12573$
$S_{10} = 22.1035$; $S_{40} = 22.1035$

\(S =\)	\(1\)	\(+\)	\(2\)	\(+\)	\(3\)	\(+\)	\(\cdots\)	\(+\)	\(100\)
\(+\ S =\)	\(100\)	\(+\)	\(99\)	\(+\)	\(98\)	\(+\)	\(\cdots\)	\(+\)	\(1\)
\(2S =\)	\(101\)	\(+\)	\(101\)	\(+\)	\(101\)	\(+\)	\(\cdots\)	\(+\)	\(101\)

Search

Text Color

Text Size

Margin Size

Font Type