5.A: Answers
- Page ID
- 212052
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Section 5.1
- \((8)(6)(1)+(6)(4)(2)+(3)(3)(1) = 105\)
- \(\pi(4)^2(0.5)+ \pi(3)^2(1.0)+\pi(1)^2(2.0) = 19\pi\)
- \((9)(0.2)+(6)(0.2)+(2)(0.2) = 3.4\)
- \(\displaystyle \int_0^3 (5-x)^2\, dx = 39\)
- \(\displaystyle \int_0^4 \frac12 (x+1)\sqrt{x} \ dx = \frac{136}{15}\)
- \(\displaystyle \int_0^4 \pi\left[\frac{4-x}{2} \right]^2\, dx = \frac{16\pi}{3}\)
- If \(A(y)\) is the cross-sectional area of object \(A\) at height \(y\) above the base and \(B(y)\) is the cross-sectional area of object \(B\) at height \(y\) above its base, then we know that \(A(y) = B(y)\) for all values of \(y\), so Vol(\(A\)) \(\displaystyle = \int_a^b A(y) \, dy = \int_a^b B(y) \, dy =\) Vol (\(B\)): the volumes are equal.
- \(\displaystyle \int_1^4 \left[\frac{1}{x} \right]^2\, dx = \frac{3}{4}\)
- \(\displaystyle \int_0^4 \pi\left[3-\sqrt{x} \right]^2\, dx = 12\pi\)
- \(\displaystyle \int_0^{\pi} \left[\sin(x) \right]^2\, dx = \frac{\pi}{2}\)
- \(\displaystyle \int_0^{\frac{\pi}{2}} \frac12 \cdot \pi \left[\frac12 \cos(x) \right]^2\, dx = \frac{\pi^2}{32}\)
-
- \(\displaystyle \int_{-1}^{\frac32} \left[(3+x-x^2)-x^2\right]^2 \, dx = \frac{625}{48} \approx 13.021\)
- \(\displaystyle \int_{-1}^{\frac32} \frac12 \cdot \pi \left[\frac12 (3+x-2x^2)\right]^2 \, dx = \frac{625\pi}{384} \approx 5.1\)
- \(\displaystyle \int_{-1}^{\frac32} 2\left[3+x-2x^2\right]^2 \, dx = \frac{625}{24} \approx 26.0\)
- \(\displaystyle \int_{-1}^{\frac32} \frac12 \left[\frac{3+x-2x^2}{\sqrt{2}}\right]^2 \, dx = \frac{625}{192} \approx 3.3\)
- \(\displaystyle \int_{0}^{8} \left[\sqrt{8-y}\right]^2 \, dy = 32\)
- \(\displaystyle \int_{1}^{4} \frac{\pi}{2}\left[\frac{\sqrt{8-y}-2}{2}\right]^2 dy = \frac{\pi}{48}\left[299-112\sqrt{7}\right]\)
-
- \(H^2L\)
- \(\displaystyle \int_0^L \left(\frac{H}{L} x\right)^2 \, dx = \frac13 H^2 L\)
- \(\frac13\)
-
- \(BL\)
- \(\displaystyle \int_0^L \frac{B}{L^2} x^2 \, dx = \frac13 BL\)
- \(\frac13\)
Section 5.2
- \(\displaystyle \int_0^5 \pi x^2 \, dx = \frac{125\pi}{3}\)
- \(\displaystyle \int_0^{\frac{\pi}{3}} \pi \cos^2(x) \, dx = \frac{\pi}{2}\left[\frac{\pi}{3}+\frac{\sqrt{3}}{4}\right]\) (There are actually two such regions.)
- \(\displaystyle \int_0^7 \pi \left[\sqrt{7-x}\right]^2 \, dx = \frac{49\pi}{2}\)
- \(\displaystyle \int_0^{\sqrt{5}} \pi \left[5-x^2\right]^2 \, dx = \frac{40\pi\sqrt{5}}{3}\)
- \(\displaystyle \int_0^{121} \pi \left[\sqrt{121-x}\right]^2 \, dx = \frac{14641\pi}{2}\)
- \(\displaystyle \int_0^5 \pi \left[\sqrt{\frac{225-9x^2}{25}}\right]^2 \, dx = 30\pi\)
- \(\displaystyle \int_0^1 \pi \left[x^2-\left(x^4\right)^2\right] \, dx = \frac{2\pi}{9}\)
- \(\displaystyle \int_0^1 \pi \left[\left(\sqrt[4]{y}\right)^2-\left(\sqrt{y}\right)^2\right] \, dy = \frac{\pi}{6}\)
- \(\displaystyle \int_0^1 \pi \left[\left(x^2\right)^2-\left(x^3\right)^2\right] \, dx = \frac{2\pi}{35}\)
- \(\displaystyle \int_0^{\frac{\pi}{3}} \pi \left[\sec^2(x)-\cos^2(x)\right] \, dx = \pi\left[\sqrt{3}-\frac{\pi}{6}-\frac{\sqrt{3}}{8}\right]\)
- \(\displaystyle \int_0^1 \pi \left[\left(x-(-4)\right)^2-\left(x^4-(-4)\right)^2\right] \, dx = \frac{118\pi}{45}\)
- \(\displaystyle \int_0^1 \pi \left[\left(3-y\right)^2-\left(3-\sqrt[4]{y}\right)^2\right] \, dy = \frac{22\pi}{15}\)
- \(\displaystyle \int_0^1 \pi \left[\left(3-\sin(x)\right)^2-\left(3-x\right)^2\right] \, dx = \pi\left[6\cos(1)-\frac14\sin(2)-\frac{17}{6}\right]\)
- \(\displaystyle \int_0^1 \pi \left[\left(y^2-(-2)\right)^2-\left(y^3-(-2)\right)^2\right] \, dy = \frac{41\pi}{105}\)
- \(\displaystyle \int_0^1 \pi \left[\left(2-\sqrt{x}\right)^2-\left(2-\sqrt[3]{x}\right)^2\right] \, dx = \frac{7\pi}{30}\)
- \(\displaystyle \int_{-2}^2 \pi \left[\sqrt{4-x^2}\right]^2 \, dx = \frac{32\pi}{3} = \frac43 \pi \left(2\right)^3\)
- \(\displaystyle \int_{-5}^5 \pi \left[3\sqrt{1-\frac{x^2}{25}}\right]^2 \, dx = 60\pi\)
- \(\displaystyle \int_1^2 \pi \left[\left(x^2)\right)^2-(1)^2\right] \, dx = \frac{26\pi}{5}\)
- \(\displaystyle \int_0^{\pi} \pi \left|\frac12-\sin(x)\right|^2 \, dx = \pi\left[\frac{3\pi}{4}-2\right]\)
-
- \(\displaystyle \int_{1}^{10} \frac{1}{x} \, dx = \ln(10)\); \(\displaystyle \int_{1}^{100} \frac{1}{x} \, dx = \ln(100)\); \(\displaystyle \int_{1}^{M} \frac{1}{x} \, dx = \ln(M)\); \(\displaystyle \lim_{M\to \infty} \, \ln(M) = \infty\)
- \(\displaystyle \int_{1}^{10} \frac{\pi}{x^2} \, dx = \frac{9}{10}\pi\); \(\displaystyle \int_{1}^{100} \frac{\pi}{x^2} \, dx = \frac{99}{100}\pi\); \(\displaystyle \int_{1}^{M} \frac{\pi}{x^2} \, dx = \left[1-\frac{1}{M}\right]\pi\); \(\displaystyle \lim_{M\to \infty} \, \left[1-\frac{1}{M}\right]\pi = \pi\)
Section 5.3
- \(\sqrt{15^2+20^2}+\sqrt{\left(-24\right)^2+18^2}+\sqrt{12^2+\left(-12\right)^2} \approx 71.97\) ft
- \(\sqrt{\left(1-0\right)^2 + \left(2-1\right)^2}+\sqrt{\left(2-1\right)^2 + \left(4-2\right)^2} \approx 3.65\)
-
- \(\sqrt{\left(2-0\right)^2 + \left(5-1\right)^2} = 2\sqrt{5}\)
- \(\displaystyle \int_0^2 \sqrt{1+\left[2\right]^2}\, dx = 2\sqrt{5}\)
-
- \(\sqrt{\left(5-2\right)^2 + \left(-5-1\right)^2} = 3\sqrt{5}\)
- \(\displaystyle \int_0^3 \sqrt{\left[1\right]^2+\left[-2\right]^2}\, dx = 3\sqrt{5}\)
- \(\displaystyle y' = x^{\frac12} = \sqrt{x}\), so \(L = \int_0^4 \sqrt{1+\left[\sqrt{x}\right]^2}\, dx = \int_0^4 \sqrt{1+x} \, dx = \left[\frac23\left(1+x\right)^{\frac32}\right]_0^4 = \frac23\left[5\sqrt{5}-1\right]\)
- \(\displaystyle y' = x^2 -\frac14 x^{-2} \Rightarrow 1+\left[y'\right]^2 = 1 + x^4 -\frac12 +\frac{1}{16} x^{-4} = x^4 +\frac12 +\frac{1}{16} x^{-4} = \left(x^2 + \frac14 x^{-2}\right)^2\), so \(\displaystyle L = \int_1^5 \sqrt{1+\left[y'\right]^2}\, dx = \int_1^5 \left[x^2 + \frac14 x^{-2}\right] \, dx = \left[\frac13 x^3 - \frac14 x^{-1}\right]_1^5 = \left[\frac{125}{3} - \frac{1}{20}\right]-\left[\frac13 - \frac14\right] = \frac{623}{15} \approx 41.53\)
- \(\displaystyle y' = x^4 -\frac{1}{4} x^{-4} \Rightarrow 1+\left[y'\right]^2 = 1 + x^8 -\frac12 +\frac{1}{16} x^{-8} = x^8 +\frac12 +\frac{1}{16} x^{-8} = \left(x^4 + \frac14 x^{-4}\right)^2\), so \(\displaystyle L = \int_1^5 \sqrt{1+\left[y'\right]^2}\, dx = \int_1^5 \left[x^4 + \frac14 x^{-4}\right] \, dx = \left[\frac15 x^5 - \frac{1}{12} x^{-3}\right]_1^5 = \left[625 - \frac{1}{1500}\right]-\left[\frac15 - \frac{1}{12}\right] \approx 624.88\)
- \(\displaystyle L = \int_0^1 \sqrt{1+\left[2x\right]^2} \, dx = \int_0^1 \sqrt{1+4x^2}\, dx \approx 1.4789\) (using technology)
- \(\displaystyle L = \int_1^9 \sqrt{1+\left[\frac{1}{2\sqrt{x}}\right]^2} \, dx = \int_1^9 \sqrt{1+\frac{1}{4x}}\, dx \approx 8.2681\)
- \(\displaystyle L = \int_0^{\frac{\pi}{4}} \sqrt{1+\left[\cos(x)\right]^2} \, dx = \int_0^{\frac{\pi}{4}} \sqrt{1+\cos^2(x)}\, dx \approx 1.058\); \(\displaystyle L = \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \sqrt{1+\cos^2(x)}\, dx \approx 0.852\)
- \(\displaystyle \int_0^{2\pi} \sqrt{\left[-5\sin(t)\right]^2+\left[2\cos(t)\right]^2}\, dt = \int_0^{2\pi} \sqrt{25\sin^2(t)+4\cos^2(t)}\, dt \approx 23.018\)
- \(\displaystyle \int_{10}^{20} \sqrt{\left[-t\cdot \sin(t)+\cos(t)\right]^2+\left[t\cdot \cos(t)+\sin(t)\right]^2}\, dt = \int_{10}^{20} \sqrt{1+t^2}\, dt \approx 150.346\)
- \(\displaystyle \int_{0}^{2\pi} \sqrt{\left[R\left(1-\cos(t)\right)\right]^2+\left[R\sin(t)\right]^2}\, dt = R\int_{0}^{2\pi} \sqrt{2\left(1-\cos(t)\right)}\, dt \approx 8R\)
- \(\displaystyle \frac{5280\, \mbox{ft}}{2\pi\, \frac{\mbox{ft}}{\mbox{rev}}} \cdot 8\, \frac{\mbox{ft}}{\mbox{rev}} \approx 6723\,\mbox{feet} \approx 1.27\,\mbox{miles}\)
- \(\displaystyle L = \int_0^4 \sqrt{1+\left[2x\right]^2}\, dx = \int_0^4 \sqrt{1+4x^2}\, dx \approx 16.8186\) so we need \(a\) such that \(\displaystyle \int_0^a \sqrt{1+4x^2}\, dx \approx \frac12\left(16.8186\right) = 8.4093\) and \(b\) and \(c\) such that \(\displaystyle \int_0^b \sqrt{1+4x^2}\, dx \approx \frac13\left(16.8186\right) = 5.6062\) and \(\int_0^c \sqrt{1+4x^2}\, dx \approx \frac23\left(16.8186\right) = 11.2124\). Guessing and checking using technology yields \(a \approx 2.77\), \(b \approx 2.22\) and \(c \approx 3.23\).
- \(\displaystyle y = \frac23 x^{\frac32} + \frac{1}{2x^{\frac12}}\)
-
- A: \(2\pi(3)(4)=24\pi\); B: \(2\pi(1)(2) = 4\pi\)
- A: \(2\pi(5)(4)=40\pi\); B: \(2\pi(8)(2) = 32\pi\)
-
- A: \(2\pi(3)(3)=18\pi\); B: \(2\pi(4)(5) = 40\pi\)
- A: \(2\pi(2)(3)=12\pi\); B: \(2\pi(6.5)(5) = 65\pi\)
- \(\theta = \frac{\pi}{2} = 90^{\circ}\) results in the midpoint of the line segment being furthest from the \(x\)-axis.
- \(\displaystyle \int_0^1 2\pi x \sqrt{1+\left[6x^2\right]^2}\, dx \approx 10.207\)
- \(\displaystyle \int_0^1 2\pi \left(2x^2\right) \sqrt{1+\left[4x\right]^2}\, dx \approx 13.306\)
- \(\displaystyle \int_0^2 2\pi x^3 \sqrt{1+\left[3x^2\right]^2}\, dx =\frac{\pi}{27}\left[145\sqrt{145}-1\right]\)
- \(\displaystyle \int_0^2 2\pi x \sqrt{1+\left[2x\right]^2}\, dx =\frac{\pi}{4}\left[17\sqrt{17}-1\right]\)
- Rotate \(\displaystyle y = \sqrt{R^2-x^2}\) about the \(x\)-axis to get a sphere of radius \(R\). Then:\[\displaystyle y = \left[R^2-x^2\right]^{\frac12} \Rightarrow y' = -x\left[R^2-x^2\right]^{-\frac12} \Rightarrow 1+\left[y'\right]^2 = 1 + \frac{x^2}{1-x^2} = \frac{1}{1-x^2}\nonumber\]so the slice from \(x=a\) to \(x=b\) has surface area:\[\int_a^b 2\pi \sqrt{R^2-x^2}\cdot \sqrt{\frac{1}{R^2-x^2}}\, dx = 2\pi(b-a)\nonumber\]which depends only on the width of the slice.
- Cake: no; frosting: yes.
-
- \(\displaystyle \int_c^d 2\pi \cdot y \sqrt{1+\left[g'(y)\right]^2}\, dy\)
- \(\displaystyle \int_c^d 2\pi \cdot g(y) \sqrt{1+\left[g'(y)\right]^2}\, dy\)
-
- \(\displaystyle \int_0^1 2\pi \cdot y \sqrt{1+\left[e^y\right]^2}\, dy \approx 7.055\)
- \(\displaystyle \int_0^1 2\pi \cdot e^y \sqrt{1+\left[e^y\right]^2}\, dy \approx 22.943\)
-
- \(\displaystyle \int_{\alpha}^{\beta} 2\pi \cdot y(t) \sqrt{\left[x'(t)\right]^2+\left[y'(t)\right]^2}\, dt\)
- \(\displaystyle \int_{\alpha}^{\beta} 2\pi \cdot x(t) \sqrt{\left[x'(t)\right]^2+\left[y'(t)\right]^2}\, dt\)
-
- \(\displaystyle \int_{0}^{\frac{\pi}{2}} 2\pi \sin(t) \sqrt{\left[-\sin(t)\right]^2+\left[\cos(t)\right]^2}\, dt = 2\pi\)
- \(\displaystyle \int_{0}^{\frac{\pi}{2}} 2\pi \cos(t)\sqrt{\left[-\sin(t)\right]^2+\left[\cos(t)\right]^2}\, dt = 2\pi\)
- \(\displaystyle \int_{0}^{4\pi} \sqrt{\left[-\sin(t)\right]^2+\left[\cos(t)\right]^2+\left[1\right]^2}\, dt = 4\pi\sqrt{2}\)
- \(\displaystyle \int_{0}^{1} \sqrt{\left[1\right]^2+\left[2t\right]^2+\left[3t^2\right]^2}\, dt \approx 1.863\)
- \(\displaystyle \int_{0}^{2\pi} \sqrt{\left[-3\sin(t)\right]^2+\left[2\cos(t)\right]^2+\left[7\cos(7t)\right]^2}\, dt \approx 33.293\)
Section 5.4
- A “slice” of water \(y\) ft high with thickness \(\Delta y\) ft:

has volume \(3\cdot 4 \cdot \Delta y = 12\Delta y \ \mbox{ft}^3\), so its weight is \(62.5(12)\Delta y\ \mbox{lb}\); the work required to lift this slice \((7-y)\) feet is \(750(7-y)\Delta y\ \mbox{ft-lbs}\). The total work required to pump out all of the water is:\[\int_0^7 750(7-y)\, dy = 18375 \ \mbox{ft-lbs}\nonumber\] -
- A slice of oil at initial height \(y\) m with thickness \(\Delta y\) m has volume \(5\cdot 2 \cdot \Delta y\ \mbox{m}^3\), so its mass is \(900\left(10\Delta y\right) = 9000\Delta y\ \mbox{kg}\) and the force required to lift it is \((9000\Delta y)(9.81) = 88290\Delta y\ \mbox{N}\). Lifting this slice \((4-y)\ \mbox{m}\) requires \(88290(4-y)\Delta y\) N-m of work, so the total work needed to empty the tank is:\[\int_0^4 88290(4-y)\, dy = 706320\,\mbox{J}\nonumber\]
- The top \(10\,\mbox{m}^3\) corresponds to the top \(1\,\mbox{m}\) of oil, so the work required is:\[\int_3^4 88290(4-y)\, dy = 44145\,\mbox{J}\nonumber\]
- \(\displaystyle \frac{706320\,\mbox{J}}{200\,\frac{\mbox{J}}{\mbox{sec}}} = 3531.15\,\mbox{sec} \approx 59\,\mbox{min}\)
-
- A slice of water at initial height \(y\) m with thickness \(\Delta y\) m has volume \(\pi\left(1\right)^2\Delta y\ \mbox{m}^3\), so its mass is \(1000\left(\pi\Delta y\right) = 1000\pi\Delta y\ \mbox{kg}\) and the force required to lift it is \((1000\pi\Delta y)(9.81) = 9810\pi\Delta y\ \mbox{N}\). Lifting this slice \((6-y)\ \mbox{m}\) requires \(9810\pi(6-y)\Delta y\) N-m of work, so the total work needed to empty the tank is:\[\int_0^6 9810\pi(6-y)\, dy = 176580\pi \approx 554742\ \mbox{J}\nonumber\]
- The distance each slice must be lifted is now \((6-y)+2 = 8-y\) so the total work done is:\[\int_5^6 9810\pi(8-y)\, dy = 24525\pi \approx 77048\ \mbox{J}\nonumber\]
- The work needed to remove half the water is:\[\int_3^6 9810\pi(6-y)\, dy = 44145\pi \approx 138686\ \mbox{J}\nonumber\]and \(\frac12 \ \mbox{hp} = \frac12\left(746\ \mbox{watts}\right) = 373 \ \mbox{watts}\) so:\[\frac{138686\,\mbox{J}}{373\,\frac{\mbox{J}}{\mbox{sec}}} = 372\,\mbox{sec} \approx 6.2\,\mbox{min}\nonumber\]
-
- Using similar triangles on a cross-section of the cone and a slice of radius \(r\) at height \(y\):

reveals that \(\displaystyle \frac{r}{y} = \frac48 \Rightarrow r = \frac12 y\) so the volume of the slice is \(\displaystyle \pi\left[\frac{y}{2}\right]^2 \Delta y \ \mbox{ft}^3\) and its weight is \(\displaystyle 25\cdot \pi \frac{y^2}{4} \Delta y \ \mbox{lb}\). The work required to lift this slice \(8-y\) ft to the top edge of the cone is thus \(\displaystyle \frac{25\pi}{4} y^2\left(8-y\right) \Delta y \ \mbox{ft-lb}\), so the total work needed to empty the container is:\[\int_0^8 \frac{25\pi}{4}y^2 \left(8-y\right)\, dy = \frac{6400\pi}{3} \approx 6702 \ \mbox{ft-lbs}\nonumber\] - \(\displaystyle \int_6^8 \frac{25\pi}{4}y^2 \left(8-y\right)\, dy = \frac{1675\pi}{3} \approx 1754 \ \mbox{ft-lbs}\)
- Using similar triangles on a cross-section of the cone and a slice of radius \(r\) at height \(y\):
- Half the work is 3351 ft-lbs, so find \(h\) so that:\[3351 = \int_0^h \frac{25\pi}{4}y^2 \left(8-y\right)\, dy = \frac{25\pi}{48}\left[32h^3-3h^4\right]\nonumber\]Solving this equation using technology yields \(h \approx 4.9\) so you should dig from the top down to a depth of 3.1 ft and leave the rest for your friend.
- Using similar triangles on a cross-section of the trough and a slice of width \(w\) at height \(y\):

with thickness \(\Delta y\) reveals that \(\frac{w}{y} = \frac64 \Rightarrow w = \frac32 y\) so the weight of this slice, which must be lifted \(\left(4-y\right)\ \mbox{ft}\), is \(80\left(\frac32 y\right)(7)\Delta y \ \mbox{lb}\) and the total work needed is:\[\int_0^4 840y(4-y)\, dy = 8960 \ \mbox{ft-lbs}\nonumber\] - If the bottom 70 ft\(^3\) of slop has depth \(h\) ft:\[\frac12 h\left(\frac32 h\right)(7) = 70 \Rightarrow h = \sqrt{\frac{40}{3}} \approx 3.65 \ \mbox{ft}\nonumber\]so the work needed to remove the top 14 ft\(^3\) is:\[\int_{3.65}^4 840y(4-y)\, dy \approx 192.21 \ \mbox{ft-lbs}\nonumber\]
-
- A horizontal slice at height \(y = \frac12 x^2\) is (approximately) a disk with radius \(x = \sqrt{2y}\) and thickness \(\Delta y\):

has volume \(\displaystyle \pi\left[\sqrt{2y}\right]^2 \Delta y = 2\pi y\Delta y \ \mbox{m}^3\) and mass \(\displaystyle 2000\pi y\Delta y \ \mbox{m}^3\); that slice must be lifted \(\left(2-y\right)\ \mbox{m}\) so the total work required is:\[\int_0^2 2000\pi y (9.81)(2-y)\, dy \approx 82184 \ \mbox{J}\nonumber\] - Each slice is lifted \((2-y)+3 = (5-y) \ \mbox{m}\), so the work needed is now:\[\int_0^2 2000\pi y (9.81)(5-y)\, dy \approx 452012 \ \mbox{J}\nonumber\]
- A horizontal slice at height \(y = \frac12 x^2\) is (approximately) a disk with radius \(x = \sqrt{2y}\) and thickness \(\Delta y\):
- Rotate the circle \(x^2+y^2=16\) about the \(x\)-axis to generate the sphere. A slice at height \(y\) (for \(-4 \leq y \leq 4\)) and thickness \(\Delta y\) is (approximately) a disk with radius \(x = \sqrt{16-y^2}\):

so the slice has volume \(\pi\left[\sqrt{16-y^2}\right]^2 \Delta y\) and mass \(1000\pi\left[16-y^2\right]\Delta y\); the slice must be lifted \(\left(4-y\right)\ \mbox{m}\), so the total work is:\[\int_{-4}^{-2} (9.81)1000\pi\left(16-y^2\right)\left(4-y\right)\, dy = 876360\pi \approx 2753166 \ \mbox{J}\nonumber\] -
- The leftmost container: more water is near the bottom, so more of the water must be lifted a greater distance.
- The rightmost container.
-
- 85 ft-lbs
- 35 ft-lbs
-
- \(\displaystyle \int_0^3 6x \, dx = 27\ \mbox{in-oz} \approx 0.14 \ \mbox{ft-lbs}\)
- \(\displaystyle \int_0^6 6x \, dx = 108\ \mbox{in-oz} \approx 0.56 \ \mbox{ft-lbs}\)
-
- The average force between \(x = 23\) and \(x = 33\) is \(\approx 15\ \mbox{dyn}\) so the work done is about:\[15(33-23) = 150 \ \mbox{dyn-cm} = 0.000015 \ \mbox{J}\nonumber\]
- The area under the graph between \(x = 28\) and \(x = 33\) is about \(90 \ \mbox{dyn-cm} = 0.000009\) J.
- Converting cm to m and applying Hooke's Law yields \(3(9.8) = k(0.15) \Rightarrow k = 196\) so the total work is:\[\int_{0.15}^{0.19} 196x \, dx = \left[98x^2\right]_{0.15}^{0.19} = 1.3328 \ \mbox{J}\nonumber\]
-
- Ceres’ radius is \(475 \ \mbox{km} = 475000 \ \mbox{m}\) and:\[GMm = \left(6.673\times 10^{-11}\right)\left(896\times 10^{18}\right)\left(100\right)\nonumber\]or \(5.979\times 10^{12}\); the work to lift the payload from \(x = 475000\ \mbox{m}\) to \(x = 485000\ \mbox{m}\) is:\[\int_{475000}^{485000} \frac{5.979\times 10^{12}}{x^2} \, dx \approx 259530 \ \mbox{J}\nonumber\]
- \(\displaystyle \int_{475000}^{575000} \frac{5.979\times 10^{12}}{x^2} \, dx \approx 2189110 \ \mbox{J}\)
- \(\displaystyle \int_{475000}^{975000} \frac{5.979\times 10^{12}}{x^2} \, dx \approx 6455070 \ \mbox{J}\)
-
- Answers will depend on your mass. If your mass (including a space suit to ensure your survivial) is 100 kg then:\[GMm = \left(6.673\times 10^{-11}\right)\left(7.35\times 10^{22}\right)\left(100\right)\nonumber\]or \(4.905\times 10^{14}\); the work done lifting you from \(x = 1737500\ \mbox{m}\) to \(x = 1937500\ \mbox{m}\) is:\[\int_{1737500}^{1937500} \frac{4.905\times 10^{14}}{x^2} \, dx \approx 29138818 \ \mbox{J}\nonumber\]
- \(\displaystyle \int_{1737500}^{2137500} \frac{4.905\times 10^{14}}{x^2} \, dx \approx 52824758 \ \mbox{J}\)
- \(\displaystyle \int_{1737500}^{11737500} \frac{4.905\times 10^{14}}{x^2} \, dx \approx 240496104 \ \mbox{J}\)
- We know that \(-0.1 = \frac{k}{10^2} \Rightarrow k = -10\).
- \(\displaystyle \int_{20}^{10} \frac{-10}{x^2} \, dx = 0.5 \ \mbox{J}\)
- \(\displaystyle \int_{10}^{1} \frac{-10}{x^2} \, dx = 9 \ \mbox{J}\)
- \(\displaystyle \int_{1}^{0.1} \frac{-10}{x^2} \, dx = 90 \ \mbox{J}\)
- \(\displaystyle \int_0^{2\pi} t \sqrt{\left[-\sin(t)\right]^2+\left[\cos(t)\right]^2}\, dt = \int_0^{2\pi} t \, dt = 2\pi^2\)
- \(\displaystyle \int_0^{1} t \sqrt{\left[2t\right]^2+\left[1\right]^2}\, dt = \int_0^{1} t\sqrt{1+4t^2} \, dt = \frac{5\sqrt{5}-1}{12}\)}
- This is the same as Problem 31. To solve without calculus, “unroll” the region to get a triangle with base \(2\pi\) (the circumference of the circle upon which the region was originally sitting) and height \(2\pi\). The area of the triangle is then \(\displaystyle \frac12\left(2\pi\right)\left(2\pi\right) = 2\pi^2\).
Section 5.5
Graphs of the regions from Problems 1, 3, 5 and 7 appear below:

- A vertical slice rotated around the \(y\) axis results in a tube: \(\displaystyle \int_0^1 2\pi x \sqrt{1-x^2}\, dx = \frac{2\pi}{3} \approx 2.09\)
- We need to split this region into two pieces. The curves intersect where \(x^2=2x \Rightarrow x^2-2x=0 \Rightarrow x(x-2) =0 \Rightarrow x = 0\) or \(x =2\). For \(0\leq x\leq2\), \(y = 2x\) is the top curve and \(y=x^2\) is the bottom curve, so the height of a vertical slice is \(2x-x^2\); for \(2 \leq x \leq 3\), the roles are reversed, so the height is \(x^2-2x\):\[\int_0^2 2\pi \left(4-x\right) \left[2x-x^2\right]\, dx + \int_2^3 2\pi \left(4-x\right) \left[x^2-2x\right]\, dx = 8\pi+\frac{7\pi}{2} = \frac{23\pi}{2} \approx 36.13\nonumber\]
- Vertical slices yield tubes: \(\displaystyle \int_1^3 2\pi \left(5-x\right) \left[\frac{1}{x}-\frac{1}{3}\right]\, dx = \left[10\ln(3)-8\right]\pi \approx 9.38\)
- Vertical slices yield tubes, but the resulting integral requires numerical integration or tables (for now):\[\int_1^4 2\pi x \left[x-\ln(x)\right]\, dx \approx 85.83\nonumber\]Horizontal slices result in washers and require us to split the region into three pieces, but finding antiderivatives is easier: \begin{align*} \int_0^1 \pi \left[\left(e^y\right)^2-1^2\right]\, dy & + \int_1^{\ln(4)} \pi \left[\left(e^y\right)^2-y^2\right]\, dy + \int_{\ln(4)}^4 \pi\left[4^2-y^2\right]\, dy\\ &= \frac{\left(e^2-3\right)\pi}{2} + \frac{\left(50-3e^2-2\left(\ln(4)\right)^3\right)\pi}{6} + \frac{\left(4-\ln(4)\right)^2\left(8+\ln(4)\right)\pi}{3} \approx 85.83 \end{align*}
- Washers: \(\displaystyle \int_1^2 2\pi x \left[\left(6-x\right)-x^2\right]\, dx + \int_2^4 2\pi x \left[x^2-\left(6-x\right)\right]\, dx = \frac{35\pi}{6}+\frac{256\pi}{3}=\frac{541\pi}{6} \approx 283.27\)
- Tubes: \(\displaystyle \int_0^{\frac{3}{\sqrt{2}}} 2\pi x\left[\sqrt{9-x^2}-x\right]\, dx = 9\pi\left(2-\sqrt{2}\right) \approx 16.56\)
- \(\displaystyle \int_0^1 2\pi x\left[x^2-x^4\right]\, dx = \frac{\pi}{6} \approx 0.52\)
- \(\displaystyle \int_0^{\sqrt{\pi}} 2\pi x\cdot\sin\left(x^2\right)\, dx = 2\pi \approx 6.28\)
- \(\displaystyle \int_0^{\frac12} 2\pi x\cdot\frac{1}{\sqrt{1-x^2}}\, dx = \pi\left(2-\sqrt{3}\right) \approx 0.84\)
- \(\displaystyle \int_0^1 2\pi \left(3-x\right)\left[x-x^4\right]\, dx = \frac{22\pi}{15} \approx 4.61\)
- \(\displaystyle \int_0^1 \pi \left[\left(x-\left(-3\right)\right)^2 - \left(x^4-\left(-3\right)\right)^2\right]\, dx = \frac{91\pi}{45}\)
- \(\displaystyle \int_0^1 2\pi \left(2-x\right)\cdot \frac{1}{1+x^2}\, dx = \pi\left[\pi-\ln(2)\right] \approx 7.69\)
- \(\displaystyle \int_0^1 2\pi \left(x+2\right)\left[1-\frac{1}{1+x^2}\right]\, dx = \pi\left[5-\pi-\ln(2)\right] \approx 3.66\)
- Slicing horizontally results in washers and requires us to split the region into two pieces:\[\int_{y=0}^{y=1} \pi\left[\left(4-\left(1+y^2\right)\right)^2 - \left(4-\left(2+y^2\right)\right)^2\right]\, dy + \int_{y=1}^{y=\sqrt{2}} \pi\left[\left(4-\left(1+y^2\right)\right)^2-\left(4-3\right)^2\right]\, dy\nonumber\]which evaluates to \(\displaystyle = \frac{13\pi}{3}+\frac{\left(24\sqrt{2}-31\right)\pi}{5} \approx 15.46\).
- Slicing horizontally results in tubes and requires us to split the region into two pieces:\[\int_{y=0}^{y=1} 2\pi\left(4-y\right)\left[\left(2+y^2\right)-\left(1+y^2\right)\right]\, dy + \int_{y=1}^{y=\sqrt{2}} 2\pi\left(4-y\right)\left[3-\left(1+y^2\right)\right]\, dy\nonumber\]which evaluates to \(\displaystyle = 7\pi + \frac{\left(64\sqrt{2}-83\right)\pi}{6} \approx 25.92\).
Section 5.6
-
- The total mass is \(m = 2+5+5=12\) and \(M_0 = 2\cdot 4+5\cdot 2 + 5\cdot 6 = 48\) so \(\displaystyle \overline{x} = \frac{48}{12} =4\).
- The total mass is now \(m = 2+5+5+8=20\) and if the new object is located at \(x=b\) then \(M_0 = 2\cdot 4+5\cdot 2 + 5\cdot 6 + 8 \cdot b= 48+8b\) so:\[5 =\overline{x} = \frac{48+8b}{20} = 2.4 + 0.4b \ \Rightarrow \ b = 6.5\nonumber\]
- If the new mass is \(\mu\), the total mass becomes \(m = 12+\mu\) and \(M_0 = 48 + \mu \cdot 10\) so:\[6 =\overline{x} = \frac{48+10\mu}{12+\mu} \ \Rightarrow \mu = 6\nonumber\]
-
- \(m = 2+5+5=12\), while \(M_y = 2\cdot 4+5\cdot 2 + 5\cdot 6 = 48\) and \(M_x = 2\cdot 3+5\cdot 4 + 5\cdot 2 = 36\), so \(\displaystyle \overline{x} = \frac{48}{12} =4\) and \(\displaystyle \overline{x} = \frac{36}{12} =3\)
- The total mass is now \(m = 2+5+5+10=22\) and if the new object is located at \((b,c)\) then \(M_y = 48+10b\) and \(M_x = 36+10c\) so: \begin{align*}5 &=\overline{x} = \frac{48+10b}{22} = \frac{24}{11} + \frac{5}{11} b \ \Rightarrow \ b = 6.2\\ 2 &=\overline{y} = \frac{36+10c}{22} = \frac{18}{11} + \frac{5}{11} c \ \Rightarrow \ c = 0.8\end{align*} You should locate the new object at \((6.2,0.8)\).
- Split the region into two rectangles, \(A\) and \(B\) (see figure below left). Then \(A\) has mass \(6\) and center of mass \((0.5, 4)\), while \(B\) has mass \(6\) and center of mass \((3, 0.5)\). The total mass is \(m=12\), \(M_y = (6)(0.5) + (6)(3) = 21\) and \(M_x = (6)(4) + (6)(0.5) = 27\), so \(\overline{x} = \frac{21}{12} = 1.75\) and \(\overline{y} = \frac{27}{12} = 2.25\). Note the center of mass \((1.75, 2.25)\) is not in the region!

- Split the region into three rectangles, \(A\), \(B\) and \(C\) (see figure above right). Then \(A\) has mass \(3\) and center of mass \((1.5, 0.5)\), while \(B\) has mass \(2\) and center of mass \((2, 1.5)\), and \(C\) has mass \(1\) and center of mass \((2.5, 2.5)\). The total mass is \(m=6\), \(M_y = (3)(1.5)+(2)(2)+(1)(2.5) = 11\) and \(M_x = (3)(0.5)+(2)(1.5)+(1)(2.5) = 7\), so \(\overline{x} = \frac{11}{6}\) and \(\overline{y} = \frac{7}{6}\).
- Split the region into three pieces, \(A\), \(B\) and \(C\) (see below left); assume \(\rho = 1\). \(A\) has mass \((8)(4) = 32\) and center of mass \((2 , 4)\), while \(B\) has mass \(\frac12 \pi\left(2^2\right) = 2\pi\) and center of mass \(\left(2, 8+ \frac{4}{3\pi}(2)\right)\), and \(C\) has mass \(\frac12 \pi \left(4^2\right) = 8\pi\) and center of mass \(\left(4+\frac{4}{3\pi}(4), 4\right)\). The total mass is \(32+10\pi\), while: \begin{align*}M_y &= (32)(2)+(2\pi)(2)+(8\pi)\left(4+\frac{16}{3\pi}\right) \approx 219.76\\ M_x &= (32)(4) + (2\pi)\left(8+ \frac{8}{3\pi}\right) + (8\pi)(4) = 284.13\end{align*} so \(\overline{x} \approx \frac{219.76}{63.42} \approx 3.47\) and \(\overline{y} \approx \frac{284.13}{63.42} \approx 4.48\)

- See above right. With \(\rho=1\), \(m = \int_0^3 x\, dx = \frac92\), \(\displaystyle M_y = \int_0^3 x\cdot x\, dx = 9\) and \(\displaystyle M_x = \int_0^3 \frac12\cdot\left[x\right]^2\, dx = \frac92\) so \(\overline{x} = \frac{9}{4.5} = 2\) and \(\overline{y} = \frac{4.5}{4.5} = 1\).
- See below left. The region is symmetric about the \(y\)-axis, so \(\overline{x} = 0\). With \(\rho =1\), \(m = \int_{-2}^{2} \left[4-x^2\right]\, dx = \frac{32}{3}\) and:\[M_x = \int_{-2}^{2} \frac12\left[\left(4\right)^2-\left(x^2\right)^2\right]\, dx = \frac{128}{5}\nonumber\]so \(\displaystyle \overline{y} = \frac{\frac{128}{5}}{\frac{32}{3}} = \frac{12}{5} = 2.4\).

- See above right. By symmetry, \(\overline{x} = 0\). With \(\rho =1\), \(m = \int_{-2}^{2} \left(4-x^2\right)\, dx = \frac{32}{3}\) and:\[M_x = \int_{-2}^{2} \frac12\left[4-x^2\right]^2\, dx = \frac{256}{15}\nonumber\]so \(\displaystyle \overline{y} = \frac{\frac{256}{15}}{\frac{32}{3}} = \frac{8}{5} = 1.6\).
- If \(\rho =1\), \(m = \int_{0}^{3} \left[\left(9-x\right)-3\right]\, dx = \frac{27}{2}\), while \(M_y = \int_{0}^{3} x\cdot \left[\left(9-x\right)-3\right]\, dx =18\) and \(M_x = \int_{0}^{3} \frac12 \left[\left(9-x\right)^2-3^2\right]\, dx =72\) so \(\displaystyle \overline{x} = \frac{18}{\frac{27}{2}} = \frac{4}{3}\) and \(\displaystyle \overline{y} = \frac{72}{\frac{27}{2}} = \frac{16}{3}\). (See below left.)

- See above right. If \(\rho =1\), \(m = \int_{0}^{9} \sqrt{x}\, dx = 18\), \(M_y = \int_{0}^{9} x\cdot \sqrt{x}\, dx = 97.2\) and \(M_x = \int_{0}^{9} \frac12 \left[\sqrt{x}\right]^2\, dx = 20.25\) so \(\displaystyle \overline{x} = \frac{97.2}{18} = 5.4\) and \(\displaystyle \overline{y} = \frac{20.25}{18} = 1.125\).
- If \(\rho =1\), \(m = \int_{0}^{1} \left[e-e^x\right]\, dx = 1\), while: \begin{align*}M_y &= \int_{0}^{1} x\cdot \left[e-e^x\right]\, dx \approx 0.359\\ M_x &= \int_{0}^{1} \frac12 \left[e^2-\left(e^x\right)^2\right]\, dx =\frac14\left(e^2+1\right) \approx 2.097\end{align*} so \(\displaystyle \overline{x} \approx 0.359\) and \(\displaystyle \overline{y} \approx 2.097\). (See below left.)
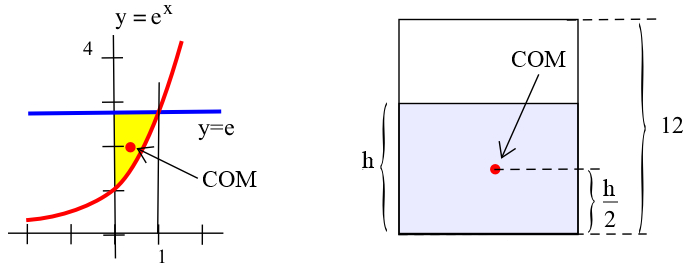
-
- The box has weight \(10\) and center of mass located \(6\) inches above the center of its base. If the box is filled with liquid to a height \(h\) inches, then the weight of the liquid is \(\left(\frac{h}{12}\right)(60) = 5h\) and the liquid’s center of mass is located \(\frac{h}{2}\) inches above the center of the box’s base (see figure above right). The total weight is thus \(10+5h\) and the moment of the system about the base of the box is \((10)(6)+(5h)\left(\frac{h}{2}\right) = 60+\frac52 h^2\), making the height of the system's center of gravity:\[H = \frac{60+\frac52 h^2}{10+5h}\nonumber\]
- To minimize \(H\), compute:\[\frac{dH}{dh} = \frac{\left(10+5h\right)\cdot 5h-\left(60+\frac52 h^2\right)\cdot 5}{\left(10+5h\right)^2}\nonumber\]Set this equal to \(0\) to get \(h = -2 \pm 2\sqrt{7}\). The \(-\) option is unrealistic, so the only critical point occurs where \(h = -2+2\sqrt{7} \approx 3.3\) inches. Both “endpoints” (empty and full) have center of mass at \(6\) inches, so \(h \approx 3.3\) must yield a minimum.
- The can has mass \(15\ \mbox{g}\) and center of mass located at height \(6\ \mbox{cm}\). If the soda in the can has height \(h\), the mass of the soda is \(\left(400\ \mbox{g}\right)\left(\frac{h}{12}\right) = \frac{100h}{3}\ \mbox{g}\) and its center of mass is at height \(\frac{h}{2}\). The mass of the can-soda system is \(15 + \frac{100h}{3}\) and the moment of the system about the bottom of the can is \((15)(6)+\left(\frac{100h}{3}\right)\left(\frac{h}{2}\right)\) so the height of the system’s center of mass is:\[H = \frac{90+\frac{50h^2}{3}}{15 + \frac{100h}{3}} = \frac{54+10h^2}{9+20h}\nonumber\]
- On your own.
- Yes. (What are the only shapes that have exactly two lines of symmetry?)
- The center of gravity of the water is 2 feet above the bottom of the box, so the total work is \(\left(300\ \mbox{lb}\right)\left(8\ \mbox{ft}\right) = 2400\ \mbox{ft-lbs}\).
- The center of gravity of the water is at the center of the sphere. The total volume of water is \(\frac43 \pi \left(2\right)^3 = \frac{32\pi}{3}\ \mbox{m}^3\), so the total mass of water is \(\frac{32000\pi}{3}\ \mbox{kg}\) and the total work is \(\left(\frac{32000\pi}{3}\ \mbox{kg}\right)\left(9.81\ \frac{\mbox{m}}{\mbox{sec}^2}\right)\left(5\ \mbox{m}\right) \approx 1643681\ \mbox{J}\).
- The area of the square is \(4\ \mbox{cm}^2\). Using Pappus’ Theorem about solids of revolution:
- \(\left(4\ \mbox{cm}^2\right)\left(2\pi\cdot 4\ \mbox{cm}\right) = 32\pi\ \mbox{cm}^3\)
- \(\left(4\ \mbox{cm}^2\right)\left(2\pi\cdot 3\ \mbox{cm}\right) = 24\pi\ \mbox{cm}^3\)
- \(\left(4\ \mbox{cm}^2\right)\left(2\pi\cdot 2\ \mbox{cm}\right) = 16\pi\ \mbox{cm}^3\)
- \(\left(4\ \mbox{cm}^2\right)\left(2\pi\cdot 3\ \mbox{cm}\right) = 24\pi\ \mbox{cm}^3\)
- \(\left(4\ \mbox{cm}^2\right)\left(2\pi\sqrt{\left(\frac{18}{11}\right)^2+\left(\frac{32}{11}\right)^2}\ \mbox{cm}\right) \approx 20.97\ \mbox{cm}^3\)
- The perimeter of the square is \(4\ \mbox{cm}\). Using Pappus’ Theorem about surface areas of revolution:
- \(\left(4\ \mbox{cm}\right)\left(2\pi\cdot 4\ \mbox{cm}\right) = 32\pi\ \mbox{cm}^2\)
- \(\left(4\ \mbox{cm}\right)\left(2\pi\cdot 3\ \mbox{cm}\right) = 24\pi\ \mbox{cm}^2\)
- \(\left(4\ \mbox{cm}\right)\left(2\pi\cdot 2\ \mbox{cm}\right) = 16\pi\ \mbox{cm}^2\)
- \(\left(4\ \mbox{cm}\right)\left(2\pi\cdot 3\ \mbox{cm}\right) = 24\pi\ \mbox{cm}^2\)
- \(\left(4\ \mbox{cm}\right)\left(2\pi\sqrt{\left(\frac{18}{11}\right)^2+\left(\frac{32}{11}\right)^2}\ \mbox{cm}\right) \approx 20.97\ \mbox{cm}^2\)
- The area of the circle is \(4\pi\ \mbox{cm}^2\) and the perimeter is \(4\pi\ \mbox{cm}\). Using Pappus’ Theorems:
- volume \(= \left(4\pi\ \mbox{cm}^2\right)\left(2\pi\cdot 5\ \mbox{cm}\right) = 40\pi^2\ \mbox{cm}^3\); surface area \(= \left(4\pi\ \mbox{cm}\right)\left(2\pi\cdot 5\ \mbox{cm}\right) = 40\pi^2\ \mbox{cm}^2\)
- V \(= \left(4\pi\ \mbox{cm}^2\right)\left(2\pi\cdot 3\ \mbox{cm}\right) = 24\pi^2\ \mbox{cm}^3\); SA \(= \left(4\pi\ \mbox{cm}\right)\left(2\pi\cdot 3\ \mbox{cm}\right) = 24\pi^2\ \mbox{cm}^2\)
- V \(= \left(4\pi\ \mbox{cm}^2\right)\left(2\pi\cdot 4\ \mbox{cm}\right) = 32\pi^2\ \mbox{cm}^3\); SA \(= \left(4\pi\ \mbox{cm}\right)\left(2\pi\cdot 4\ \mbox{cm}\right) = 32\pi^2\ \mbox{cm}^2\)
- V \(= \left(4\pi\ \mbox{cm}^2\right)\left(2\pi\cdot 3\ \mbox{cm}\right) = 24\pi^2\ \mbox{cm}^3\); SA \(= \left(4\pi\ \mbox{cm}\right)\left(2\pi\cdot 3\ \mbox{cm}\right) = 24\pi^2\ \mbox{cm}^2\)
- V \(= \left(4\ \mbox{cm}^2\right)\left(2\pi\cdot \sqrt{\left(\frac{24}{11}\right)^2+\left(\frac{36}{11}\right)^2}\ \mbox{cm}\right) \approx 98.86\ \mbox{cm}^3\)}
- SA \(= \left(4\ \mbox{cm}\right)\left(2\pi\cdot \sqrt{\left(\frac{24}{11}\right)^2+\left(\frac{36}{11}\right)^2}\ \mbox{cm}\right) \approx 98.86\ \mbox{cm}^2\)}
- Each rectangle has area \(8\), perimeter \(12\) and a centroid \(3\ \mbox{ft}\) away from the axis, so each rectangle has volume \(8\cdot 2\pi \cdot 3 = 48\pi\ \mbox{ft}^3\) and surface area \(12\cdot 2\pi \cdot 3 = 72\pi\ \mbox{ft}^2\).
- Colorado? Hawaii?
Section 5.7
- Replace the upper (infinite) limit of the integral with a massive number \(M\): \begin{align*}\int_{10}^{\infty} \frac{1}{x^3}\, dx &= \lim_{M\to\infty} \int_{10}^{M} x^{-3}\, dx = \lim_{M\to\infty} \left[-\frac12 x^{-2}\right]_{10}^{M}\\ &= \lim_{M\to\infty} \left[-\frac{1}{2M^2}+\frac{1}{200}\right] = \frac{1}{200}\end{align*} so the improper integral converges to \(0.05\).
- Replacing the upper limit of the integral with \(M\): \begin{align*}\int_{\sqrt{3}}^{\infty} \frac{1}{1+x^2}\, dx &= \lim_{M\to\infty} \Big[\arctan(x)\Big]_{\sqrt{3}}^{M} \\ &= \lim_{M\to\infty} \left[\arctan(M)-\frac{\pi}{3}\right] = \frac{\pi}{6}\end{align*} so the improper integral converges to \(\frac{\pi}{6}\).
- Replacing the upper limit of the integral with \(M\):\[\int_{e}^{\infty} \frac{5}{x\cdot \ln(x)}\, dx = \lim_{M\to\infty} \int_{e}^{M} \frac{5}{x\cdot \ln(x)}\, dx\nonumber\]Substitute \(u = \ln(x) \Rightarrow du = \frac{1}{x}\, dx\), so \(x = e \Rightarrow u = \ln(e) = 1\) and \(x = M \Rightarrow u = \ln(M)\): \begin{align*}\int_{e}^{M} \frac{5}{x\cdot \ln(x)}\, dx &= \int_{1}^{\ln(M)} \frac{5}{u}\, du = \Big[5\ln(u)\Big]_1^{\ln(M)}\\ &= 5\ln\left(\ln(M)\right) - 0 \end{align*} Returning to the improper integral:\[\lim_{M\to\infty} \int_{e}^{M} \frac{5}{x\cdot \ln(x)}\, dx = \lim_{M\to\infty} \left[5\ln\left(\ln(M)\right)\right] = \infty\nonumber\]so the improper integral diverges.
- Replacing the upper limit of the integral with \(M\): \begin{align*}\lim_{M\to\infty} \int_3^M \frac{1}{x-2}\, dx &= \lim_{M\to\infty} \Big[\ln\left(\left|x-2\right|\right)\Big]_3^M \\ &= \lim_{M\to\infty} \left[\ln(M-2)-0\right] = \infty\end{align*} so the improper integral diverges.
- Replacing the upper limit of the integral with \(M\): \begin{align*}\lim_{M\to\infty} \int_3^M (x-2)^{-3}\, dx &= \lim_{M\to\infty} \left[-\frac12 (x-2)^{-2}\right]_3^M \\ &= \lim_{M\to\infty} \left[-\frac{1}{2(M-2)^2} + \frac12\right]\end{align*} so the improper integral converges to \(0.5\).
- Replacing the upper limit of the integral with \(M\): \begin{align*}\lim_{M\to\infty} \int_3^M (x+2)^{-2}\, dx &= \lim_{M\to\infty} \left[-(x+2)^{-1}\right]_3^M \\ &= \lim_{M\to\infty} \left[-\frac{1}{M+2} + \frac15 \right]\end{align*} so the improper integral converges to \(0.2\).
- Replacing the lower limit of the integral with \(a\): \begin{align*}\lim_{a\to 0^{+}} \int_a^4 x^{-\frac12}\, dx &= \lim_{a\to 0^{+}} \Big[2\sqrt{x}\, \Big]_a^4 \\ &= \lim_{a\to 0^{+}} \left[4-2\sqrt{a}\,\right] = 4\end{align*} so the improper integral converges to \(4\).
- Replacing the lower limit of the integral with \(a\): \begin{align*}\lim_{a\to 0^{+}} \int_a^{16} x^{-\frac14}\, dx &= \lim_{a\to 0^{+}} \left[\frac43 x^{\frac34}\right]_a^{16} \\ &= \lim_{a\to 0^{+}} \left[\frac43 \cdot 8 -\frac43 a^{\frac34} \right] = \frac{32}{3}\end{align*} so the improper integral converges to \(\frac{32}{3}\).
- Replacing the upper limit of the integral with \(b\) and using Appendix I: \begin{align*}\lim_{b\to 2^{-}} \int_0^{b} \frac{1}{\sqrt{4-x^2}}\, dx &= \lim_{b\to 2^{-}} \left[\arcsin\left(\frac{x}{2}\right)\right]_0^{b} \\ &= \lim_{b\to 2^{-}} \arcsin\left(\frac{b}{2}\right) = \frac{\pi}{2} \end{align*} so the improper integral converges to \(\frac{\pi}{2}\).
- Replacing the upper limit of the integral with \(M\): \begin{align*}\lim_{M\to\infty} \int_{-2}^M \sin(x)\, dx &= \lim_{M\to\infty} \Big[-\cos(x)\Big]_{-2}^M \\ &= \lim_{M\to\infty} \left[-\cos(M)+\cos(-2) \right]\end{align*} This limit does not exist, so the integral diverges.
- Replacing the upper limit of the integral with \(b\): \begin{align*}\lim_{b\to {\frac{\pi}{2}}^{-}} \int_{0}^{b} \tan(x)\, dx &= \lim_{b\to {\frac{\pi}{2}}^{-}} \Big[-\ln\left(\left|\cos(x)\right|\right)\Big]_{0}^{b} \\ &= \lim_{b\to {\frac{\pi}{2}}^{-}} \left[-\ln\left(\cos(b)\right)\right] = \infty \end{align*} so the improper integral diverges.
- The issue for this integrand occurs not an endpoint but at the point \(x = \frac{\pi}{2}\), so we need to split the original integral into two pieces, each of which has only one improper endpoint:\[\int_0^{\pi} \tan(x)\, dx = \int_0^{\frac{\pi}{2}} \tan(x)\, dx + \int_{\frac{\pi}{2}}^{\pi} \tan(x)\, dx\nonumber\]From Problem 21, we know the first of these two new integrals diverges, so the original integral must diverge as well.
- This integral is improper at both endpoints, so we need to split it into two pieces. We can choose any value we like at which to split the interval of integration, but \(x = 0\) works nicely:\[\int_{\infty}^{\infty} \frac{1}{1+x^2} \, dx = \int_{-\infty}^{0} \frac{1}{1+x^2} \, dx + \int_0^{\infty} \frac{1}{1+x^2} \, dx\nonumber\]The first of these new integrals converges (to \(\frac{\pi}{2}\)):\[\lim_{N\to -\infty} \int_{N}^{0} \frac{1}{1+x^2} \, dx = \lim_{N\to -\infty} \left[-\arctan\left(N\right)\right] = \frac{\pi}{2}\nonumber\]Similarly, the second integral converges (to \(\frac{\pi}{2}\)):\[\lim_{M\to \infty} \int_0^{M} \frac{1}{1+x^2} \, dx = \lim_{M\to \infty} \left[\arctan\left(M\right)\right] = \frac{\pi}{2}\nonumber\]so the original integral converges to \(\frac{\pi}{2} + \frac{\pi}{2} = \pi\).
- Converges (by the P-Test, with \(p = 5 > 1\)).
- Converges (by the P-Test, with \(p = \frac65 > 1\)).
- Diverges (by the P-Test, with \(p = \frac23 < 1\)).
- Converges (by the P-Test, with \(p = \frac74 > 1\)).
- Using the comparison \(0 < \frac{1}{x^2+5} < \frac{1}{x^2}\) and the fact that \(\int_3^{\infty} \frac{1}{x^2} \ dx\) converges (P-Test, with \(p = 2 > 1\)), the smaller integral \(\int_3^{\infty} \frac{1}{x^2+5} \ dx\) converges.
- When \(x>5\), \(x^3 + x > x^3\) so \(0 < \frac{1}{x^3+x} < \frac{1}{x^3}\). By the P-Test with \(p = 3 > 1\), we know that \(\int_3^{\infty} \frac{1}{x^3} \ dx\) converges, so the smaller integral \(\int_3^{\infty} \frac{1}{x^3+x}\, dx\) also converges.
- For \(x \geq e\), \(\ln(x) < x\), so \(x+\ln(x) < 2x\) and:\[\frac{1}{x+\ln(x)} > \frac{1}{2x} \ \Rightarrow \ \frac{7}{x+\ln(x)} > \frac72 \cdot \frac{1}{x}\nonumber\]By the P-Test with \(p = 1\), we know that \(\int_e^{\infty} \frac{1}{x} \ dx\) diverges, so \(\frac72 \int_e^{\infty} \frac{1}{x} \ dx\) diverges and the bigger integral \(\int_e^{\infty} \frac{7}{x+\ln(x)} \ dx\) must diverge as well.
- For \(x \geq \pi\), \(-1 \leq \cos(x) \leq 1\) so:\[0 \leq 1+\cos(x) \leq 2 \ \Rightarrow \ 0 \leq \frac{1+\cos(x)}{x^2} \leq \frac{2}{x^2}\nonumber\]We also know that \(\int_{\pi}^{\infty} \frac{1}{x^2} \ dx\) converges (by the P-Test with \(p = 2 > 1\)), hence \(2\cdot \int_{\pi}^{\infty} \frac{1}{x^2} \ dx\) converges, so the smaller integral \(\int_{\pi}^{\infty} \frac{1+\cos(x)}{x^2} \ dx\) converges as well.
- For \(x \geq 1\), \(x^5+1 \leq x^5+x^5 = 2x^5\) so:\[\frac{1}{x^5+1} \geq \frac{1}{2x^5} \ \Rightarrow \ \frac{x^4}{x^5+1} \geq \frac{x^4}{2x^5} = \frac12 \cdot \frac{1}{x}\nonumber\]Because \(\int_1^{\infty} \frac{1}{x}\ dx\) diverges (by the P-Test with \(p=1\)), we know that \(\int_1^{\infty} \frac12 \cdot \frac{1}{x}\ dx\) diverges, so the bigger integral \(\int_1^{\infty} \frac{x^4}{x^5+1}\ dx\) diverges as well. We can write the original integral as:\[\int_0^1 \frac{x^4}{x^5+1}\ dx + \int_1^{\infty} \frac{x^4}{x^5+1}\ dx\nonumber\]Because the second of these integrals diverges, the original integral diverges.
- Using the disk method, the volume is: \begin{align*} \int_1^{\infty} &\pi\cdot\left[\frac{1}{x}\right]^2\, dx = \lim_{M\to \infty} \pi\int_1^M x^{-2}\, dx \\ &= \lim_{M\to \infty} \pi\left[-\frac{1}{x}\right]_1^M = \lim_{M\to \infty} \pi\left[-\frac{1}{M}+1\right]\end{align*} so the volume is finite and is equal to \(\pi\).
- Using the disk method, the volume is:\[\int_0^{\infty} \pi\cdot\left[\frac{1}{1+x^2}\right]^2\, dx = \lim_{M\to \infty} \pi\int_0^M \frac{1}{\left(x^2+1\right)^2}\, dx\nonumber\]Using Appendix I to find an antiderivative: \begin{align*}&\lim_{M\to \infty} \frac{\pi}{2}\left[\frac{x}{x^2+1} + \arctan(x)\right]_0^M \\ &= \lim_{M\to \infty} \frac{\pi}{2}\left[\frac{M}{M^2+1}+\arctan(M)\right] = \frac{\pi}{2} \cdot \frac{\pi}{2}\end{align*} so the volume is finite and is equal to \(\frac{\pi^2}{4}\).
- Using the tube method, the volume is:\[\int_0^{\infty} 2\pi x \left[\frac{1}{1+x^2}\right]\, dx = \lim_{M\to \infty} \pi\int_0^M \frac{2x}{\left(x^2+1\right)}\, dx\nonumber\]Using the substitution \(u = x^2+1\), this becomes:\[\lim_{M\to \infty} \pi\left[\ln(x^2+1)\right]_0^M = \lim_{M\to \infty} {\pi}\left[\ln(M^2+1)\right] = \infty\nonumber\]so the volume is infinite.
- The sum (which is a left-endpoint Riemann sum for the integral) is larger.
- The sum is larger.
- As long as \(s > 0\): \begin{align*}F(s) &= \int_0^{\infty} e^{-st}\cdot 1 \, dt = \lim_{M\to \infty} \left[-\frac{1}{s} e^{-st}\right]_0^M \\ &= \lim_{M\to \infty} -\frac{1}{s}\left[e^{-sM}-1\right] = \frac{1}{s}\end{align*}
- As long as \(s > 0\): \begin{align*}G(s) &= \int_2^{\infty} e^{-st}\cdot 1 \, dt = \lim_{M\to \infty} \left[-\frac{1}{s} e^{-st}\right]_2^M \\ &= \lim_{M\to \infty} -\frac{1}{s}\left[e^{-sM}-e^{-2s}\right] = \frac{e^{-2s}}{s}\end{align*}
- If \(b > 0\), the integral \(\displaystyle \int_0^b \frac{1}{x^q} \ dx\) converges if \(q < 1\) and diverges if \(q \geq 1\). The proof mimics the proof of the P-Test. Rewrite the integral as:\[\lim_{a\to 0^{+}} \int_a^b \frac{1}{x^q} \ dx\nonumber\]then consider the cases \(q = 1\), \(q < 1\) and \(q > 1\).
Section 5.8
- For window \(A\), the total hydrostatic force is:\[\int_2^6 2\rho x \, dx = \rho\bigg[x^2\bigg]_2^6 = 32\rho\nonumber\]For window \(B\), the width \(w\) of a horizontal slice at depth \(x\) (see below left) satisfies:\[\frac{w}{x-2} = \frac24 \ \Rightarrow \ w = \frac12 (x-2)\nonumber\]so the total hydrostatic force is:\[\int_2^6 2\rho x\cdot \frac12 (x-2) \, dx = \frac{\rho}{2}\bigg[\frac13 x^3 - x^2\bigg]_2^6 = \frac{56\rho}{3}\nonumber\]

- For the triangular end, the width \(w\) of a horizontal slice at depth \(x\) (see above right) satisfies:\[\frac{w}{5-x} = \frac45 \ \Rightarrow \ w = \frac45 (5-x)\nonumber\]so the total hydrostatic force is:\[ \int_0^5 \rho x\cdot \frac45 (5-x) \, dx = \frac{4\rho}{5}\bigg[\frac52 x^2 - \frac13 x^3\bigg]_0^5 = \frac{50\rho}{3}\nonumber\] For the rectangular end, the total force is:\[\int_0^5 \rho x\cdot 4 \, dx = 2\rho \bigg[x^2\bigg]_0^5 = 50\rho\nonumber\]The length plays no role in the above computations, so doubling the length does not change the value of either hydrostatic force.
- A slice at height \(y\) above the bottom of the tank has width \(2\sqrt{y}\) (see below) so the total force is: \begin{align*}\int_0^4 \rho\left(4-y\right)\cdot 2\sqrt{y} \, dy &= 2\rho \int_0^4\left[4y^{\frac12} - y^{\frac32}\right]\, dy \\ &= 2\rho\left[\frac83 y^{\frac32} - \frac25 y^{\frac52}\right]_0^4 = \frac{256\rho}{15}\end{align*}
- The one with the largest perimeter (not the left one, probably the middle one).
-
- A “slice” of the cylinder at depth \(x\) of thickness \(\Delta x\) has area \(2\pi \cdot 20 \cdot \Delta x\) so the total force against the bottom 2 feet of the cylinder is:\[\int_{28}^{30} \rho x \cdot 40\pi \, dx = 20\pi\rho\bigg[x^2\bigg]_{28}^{30} = 2320\pi\rho\nonumber\]
- Only the limits of integration change:\[\int_{33}^{35} \rho x \cdot 40\pi \, dx = 20\pi\rho\bigg[x^2\bigg]_{33}^{35} = 2720\pi\rho\nonumber\]
-
- \(m = 20\) g and \(v = 3\cdot2\pi\cdot 15 = 90\pi\) cm/sec, so KE \(= \frac12\cdot20\left(90\pi\right)^2 = 81000\pi^2 \approx 799438\ \mbox{ergs} \approx 0.08\) J.
- \(m = 20\) g, \(v = 3\cdot2\pi\cdot 20 = 120\pi\) cm/sec, so KE \(= \frac12\cdot20\left(120\pi\right)^2 = 144000\pi^2 \approx 1421223\ \mbox{ergs}\)
- The kinetic energy of a vertical slice of the bar (see below) of width \(\Delta x\) cm located \(x\) cm from the axis has kinetic energy \(\frac12\left(3\,\Delta x\right)\left(2\cdot 2\pi x\right)^2 = 24\pi^2 x^2 \, \Delta x\) so the object's total kinetic energy is:\[\int_{10}^{60} 24\pi^2x^2\, dx = 8\pi^2 x^3\bigg|_{10}^{60} \approx 1.7\ \mbox{J}\nonumber\]

- The density of the bar is \(0.2\) g/cm so the kinetic energy of a vertical slice of the bar (see below) of width \(\Delta x\) cm located \(x\) cm from the axis has kinetic energy \(\frac12\left(0.2\,\Delta x\right)\left(2\pi x\right)^2 = 0.4\pi^2 x^2 \, \Delta x\) so the kinetic energy of the right half of the object is:\[\int_{0}^{50} 0.4\pi^2x^2\, dx = \frac{0.4}{3}\pi^2 x^3\bigg|_{0}^{50} \approx 164493.4\ \mbox{ergs}\nonumber\]By symmetry, the total kinetic energy of the object is \(2\cdot 164493.4 = 328,986.8\) ergs.

-
- Proceeding as in Example 5, an annular “slice” of the first washer of thickness \(\Delta x\) and radius \(x\) has (approximate) mass \(1\cdot 2\pi x \Delta x\cdot 1\) g and velocity \(6\pi x\) cm/sec so the kinetic energy of the slice is (approximately) \(\frac12\left(2\pi x\delta x\right)\left(6\pi x\right)^2 = 36\pi^3x^3\Delta x\) and the total kinetic energy of the washer is thus:\[\int_1^3 36\pi^3x^3\, dx = 9\pi^3 x^4 \bigg|_1^3 = 720\pi^3\ \mbox{ergs}\nonumber\]
- Only the height (2 cm instead of 1 cm) and the radii of the second washer differ from the first washer, so the total kinetic energy of the second washwer is:\[\int_3^4 72\pi^3x^3\, dx = 18\pi^3 x^4 \bigg|_3^4 = 3150\pi^3\ \mbox{ergs}\nonumber\]
- The mass of a vertical slice of the place of thickness \(\Delta x\) cm located \(x\) cm right of the axis is \(3\cdot 10 \cdot \Delta x\) g and its velocity is \(2\cdot 2\pi x = 4\pi x\) cm/sec so its kinetic energy is \(\frac12 \cdot 30\Delta x\left(4\pi x\right)^2 = 240\pi^2 x^2 \delta x\) and the kinetic energy of the right half of the plate is:\[\int_0^3 240\pi^2x^2\, dx = 80\pi^2 x^3 \bigg|_0^3 = 2160\pi^2\ \mbox{ergs}\nonumber\]and the kinetic energy of the entire plate is \(2\cdot2160\pi^2 = 4320\pi^2\) ergs.
- \(a\) votes for candidate \(A\), \(b\) for \(A\) and \(c\) for \(C\).
- \(B\) wins:

-
- \(A\) wins: FIGURE

- \(C\) wins:
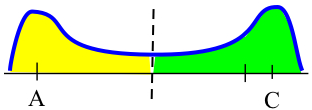
- \(B\) wins:

- \(A\) wins: FIGURE
-
- \(A\)
- \(A\)
- looks like \(C\)
- On your own.


